渐开线花键连接的非线性动力学特性

薛向珍，王三民，袁 茹

(西北工业大学 机电学院，710072西安)

渐开线花键连接由于传输扭矩能力大，对中性好，故广泛应用于航空减速器、航天发动机涡轮泵等动力传输系统中.由于花键齿侧间隙的存在，当花键副受力时，侧隙小的花键齿先啮合，间隙次之的再啮合，依次进行，实际参与啮合的齿数小于设计齿数［1］.航空花键副受力情况复杂，在变扭矩、轴向力及弯矩共同作用下，在起飞、巡航、着陆时都受到较大的变载荷冲击，且由于齿侧间隙使得花键副啮合刚度具有时变性［1］，导致花键副具有复杂的非线性动力学特性.Tjemberg［2］研究了花键副延轴向载荷分布情况并和有限元结果进行了对比，指出使载荷均匀分配的最好方法是沿轴向修正花键齿厚.Barrot等［3］研究了考虑不同载荷和几何形状下花键副轴向扭矩传递情况，指出轴向扭矩分布主要影响花键副与微动磨损相关的损坏.Silvers和Curà等［4-5］也对花键的载荷分配情况进行了研究.Leen等［6］基于由实验验证的受扭矩和轴向力载荷的花键有限元模型对花键的三维摩擦接触进行了研究，该研究考虑了轴向齿廓修形及摩擦系数的影响.Ratsimba等［7］以及Ding等［8］实验测得摩擦系数及磨损系数值，利用三维有限元模型得出接触应力和滑移距离，采用修正的Archard方程计算了磨损深度.Ding和Madge等［9-11］也对花键的磨损进行了研究.Kahraman［12］建立了渐开线花键的纯扭转动力学模型，给出了非线性动力学方程，但未对方程进行求解以及对其非线性动力学行为进行研究.为准确预估花键副的使用寿命及磨损情况，需要精确分析渐开线花键连接动载大小.

本文在考虑渐开线花键副齿侧间隙情况下，建立了渐开线花键副纯扭转动力学模型及非线性动力学方程，分析了一个次载荷循环周期中，花键副实际参与啮合的齿数分布情况，采用ANSYS计算出系统综合时变啮合刚度，利用四阶Runge-Kutta法对非线性方程进行了求解，并对花键副系统的动力学特性进行了分析，为研究花键副磨损及预估其寿命提供了理论基础.

1 花键副动力学模型与动力学方程

1.1 动力学模型

考虑齿侧间隙情况下，利用集中质量法建立了花键副的纯扭动力学模型，如图1所示，图中集中质量盘1、2、3、4分别表示花键副输入构件、外花键、内花键及花键副输出构件.

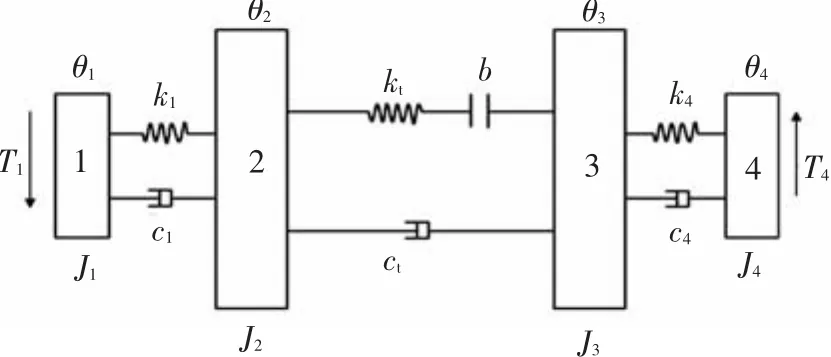
图1 花键连接动力学模型

1.2 动力学方程的建立

以4个集中质量盘的转角 θ1、θ2、θ3、θ4为广义坐标，根据Lagrange方程可推导出图1所示系统的动力学方程为

式中:Ⅰi为转动惯量;θi为转动的角度(i=1、2、3、4);T1、T4分别为输入、输出扭矩，T1=T4;b为齿侧间隙;r2、r3分别为外、内花键节圆半径;cS、ct分别为扭转阻尼、啮合阻尼;kS、kt分别为扭转刚度、综合时变啮合刚度．

对方程组(1)中的各方程两边分别除以Ⅰ1、Ⅰ2、Ⅰ3、Ⅰ4，令x1=r2(θ1-θ2)，x2=r2θ2-r3θ3，x3=r3(θ3-θ4)，则方程组(1)可化为

式中g［x(t)］为花键间隙分段线性位移函数，其表达式及式中参数含义见文献［12］．

2 花键副啮合齿对数计算

航空花键在起飞、巡航、着陆时承受着较大的变载荷冲击，所受扭矩的一个主循环伴随多个次循环，如图2所示.

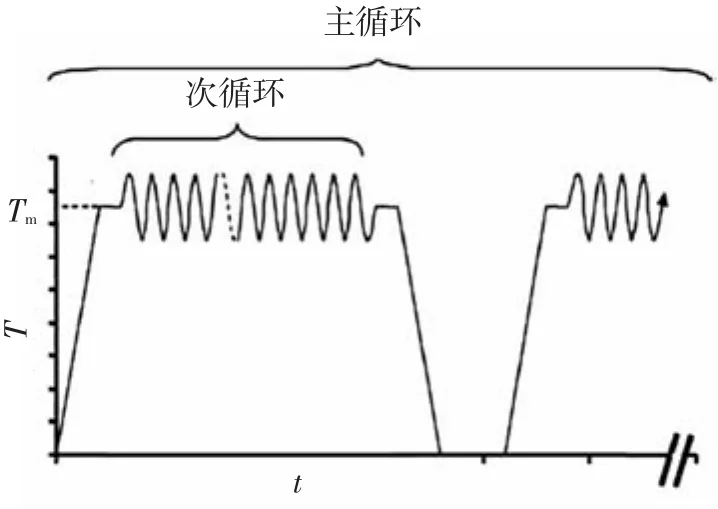
图2 系统承受扭矩形式

当花键副承受图2所示扭矩时，由于齿侧间隙的存在，间隙小的齿先啮合，间隙次之的接着啮合，直到所有载荷分配完.花键副受载时实际参与啮合的齿数rr小于设计齿数n．将花键副所受力矩中伴随一个周期次循环的扭矩值离散为T11、T12…、T1i(i=1，2，…，17)，其表达式为

式中:Tm为外激励扭矩的均值;εT为外激励扭矩的幅值波动系数;ωT为系统的角速度．

随机给定两组服从正态分布［13］的齿侧间隙值bj、b'j，采用MATLAB程序计算花键副实际参与啮合的齿数，其流程如图3所示.

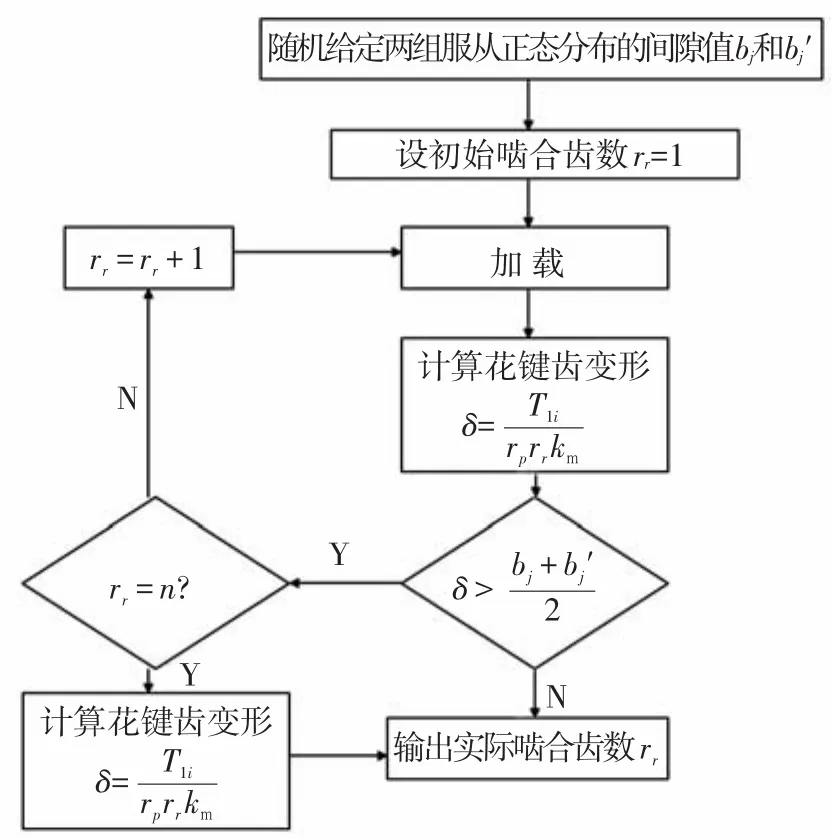
图3 实际啮合齿数计算流程

计算得出离散的扭矩分别对应的花键副啮合齿数为rr1、rr2…、rri(i=1，2，…，17)，对于齿数n=20，平均扭矩为2 600 N·m的花键副计算结果如图4所示.由图4可看出，在伴随一个次循环周期的载荷下，花键副实际参与啮合的齿数呈线性分段特征分布.波动系数为0.1时，实际参与啮合的齿数分布比较平稳，波动系数为0.5时，由于扭矩变化相对较大，且齿侧间隙不同，导致参与啮合的齿数不稳定.

图4 实际啮合齿数随波动系数变化规律

3 花键副动力学参数确定

3.1 综合时变啮合刚度计算

在PRO/E中建立花键副实体模型并导入ANSYS软件中，定义单元类型为SOLID186.定义材料弹性模量为210 GPa，泊松比0.28、密度7 800 kg/m3、摩擦系数取0.3，由于本节采用花键副全齿模型分析，为了减少不必要的单元和提高计算效率，划分网格时花键齿接触处网格细化，不会产生应力集中的部位网格相对疏松.将内花键设置为目标面，花键轴为接触面，建立接触对，接触刚度因子为1.0，最大渗透范围为0.1［14］，ICONTt初始靠近因子选用1.0×10-10.将内花键外圆柱面进行全约束，外花键轴除绕Z轴旋转的自由度外其余也全约束，在花键轴外圆柱面上连线通过轴中心对称的两条母线的各个节点处分别施加X和-X方向的力，形成力偶，力的大小Fi(i=1，2，…，17)计算如下:

式中:T1i分别为T1(t)离散的扭矩值T11、T12、…、T1i(i=1，2，…，17)，N为每条线上节点总数．求解后得出对应的接触压力Fni及变形量δi．由刚度计算公式k=Fn/δ计算出17组扭矩分别对应的时变啮合刚度，如图5、6所示．

图5 刚度随时间的变化

图6 刚度随扭矩的变化

由图5可看出，花键副啮合刚度随时间变化呈周期变化，其平均啮合刚度为245 MN/m，频率和扭矩相同;由图6可看出，由于实际参与啮合的齿对数在一定范围的扭矩值内是不变的，因此，综合时变啮合刚度随扭矩呈分段线性分布.考虑时变啮合刚度时研究花键副非线性动力学行为，需要将时变啮合刚度曲线的函数表达式代入动力学方程中.由于啮合刚度是周期性函数.因此采用傅里叶级数对其进行拟合，在初始相位为零的情况下拟合后的近似表达式为

式中:km为平均啮合刚度;ka为刚度的波动幅值;ωT为系统角速度．

3.2 啮合阻尼的计算方法

由于花键副多个键齿同时参与啮合，其啮合阻尼比较复杂，不易准确求得.因此，参照齿轮副的啮合阻尼计算经验公式，取啮合阻尼比ξ为常数，则其啮合阻尼为

式中:km为花键副的平均啮合刚度;Me、Mi分别为外、内花键副的等效质量;ξ为啮合阻尼比，其取值范围约为0.03～0.17［15］．

3.3 轴的扭转刚度

根据材料力学理论，轴的扭转刚度为

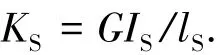
式中:G为材料的剪切弹性模量;ⅠS为轴的转动惯量，ⅠS=πd4/32;d为轴的直径;lS为轴的受扭长度．

3.4 轴的扭转阻尼

轴的扭转阻尼的经验计算公式为

式中:KS为轴的扭转刚度;ⅠS为轴的转动惯量;ξS为轴的扭转阻尼比，其取值范围为0.005～

0.075［15］．

4 非线性动力学特性分析

4.1 非线性动力学特性分析

花键副齿数n=20，m=2.5 mm，压力角为30°，利用龙格库塔法对该动力学方程进行求解.图7～10为系统平均扭矩为2 600 N·m，转速分别为300、348、360、1 080 r/min时系统第2自由度的动态响应.

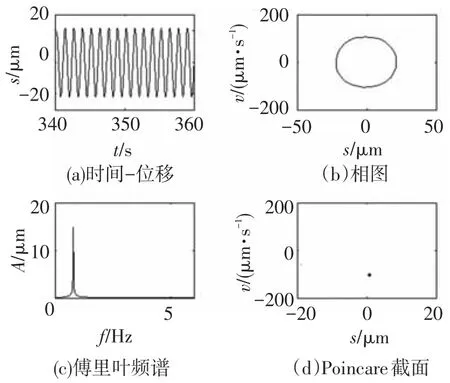
图7 转速为300 r/min时系统动态响应

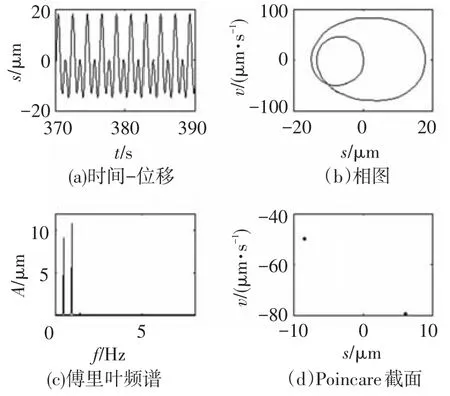
图8 转速为348 r/min时系统动态响应

图9 转速为360 r/min时系统动态响应

图10 转速为1 080 r/min时系统动态响应

可以看出，当系统转速为300 r/min时，系统呈简谐响应;当系统转速为348 r/min时，系统呈两周期响应，傅里叶频谱图上分布着两个离散的谱线;当系统转速为360 r/min时，系统呈5周期响应，其Poincare截面上有5个离散的点;当系统转速为1 080 r/min时，系统进入混沌响应.

4.2 花键副动载特性分析

花键副系统所受平均载荷Fm=Tm/r2、动态载荷为

则花键副动载系数为kv=Fd/Fm．分别改变系统所受扭矩的平均值及给定四组不同齿侧间隙b1、b2、b3、b4，且每组对应的均值σb1＜σb2＜σb3＜σb4，花键副动载系数求解结果如图11、12所示．

图11 扭矩对动载系数的影响

图12 齿侧间隙对动载系数的影响

由图11、12可看出，系统的动载系数也呈周期性变化，其值随扭矩的增大而增大，随齿侧间隙的增大而增大.

5 结 论

1)花键副啮合刚度随时间变化呈周期变化，在本文算例中其平均啮合刚度为245 MN/m，频率和扭矩相同;综合时变啮合刚度随扭矩呈分段线性分布.

2)当系统转速为300 r/min时，系统呈简谐响应;当系统转速为348 r/min时，系统呈两周期响应，傅里叶频谱图上分布着两个离散的谱线;当系统转速为360 r/min时，系统呈5周期响应，其庞加莱截面上有5个离散的点;当系统转速为1 080 r/min时，系统进入混沌响应.

3)花键副的动载系数也呈周期性变化，且随扭矩和齿侧间隙的增大而增大.因此，通过控制花键加工精度及啮合精度等措施，减小齿侧间隙，能有效提高花键副工作的稳定性.

［1］ROBINS R R.Tooth engagement evaluation of involute spline couplings［D］.［S.l.］:Engineering Brigham Young University，2008.

［2］TJEMBERG A.Load distribution in the axial direction in a spline coupling［J］.Engineering Failure Analysis，2001，8(6):557-570.

［3］BARROT A，PAREDES M，SARTOR M.Extended equations of load distribution in the axial direction in a spline coupling［J］.Engineering Failure Analysis，2009，26(1):200-211.

［4］SILVERS J，SORENSEN C D，CHASE K W.A new statistical model for predicting tooth engagement and load sharing in involute splines［C］//American Gear Manufactures Association Fall Technical Meeting 2010.Virginia:American Gear Manufacturers Association，2010:1-17.

［5］CURÀ F，MURA A，GRAVINA M.Load distribution in spline coupling teeth with parallel offset misalignment［J］.Journal of Mechanical Engineering Science，2012，27(10):2195-2205.

［6］LEEN S B，RICHARDSON I J，MCCOLL I R，et al..Macroscopic fretting variables in a splined coupling under combined torque and axial load［J］.The Journal of Strain Analysis for Engineering Design，2001，36(5):481-496.

［7］RATSIMBA C H H，MCCOLL I R，WILLIAMS E J，et al.Analysis and prediction of fretting wear damage in a representative aeroengine spline coupling［J］.Wear，2004，257(11):1193-1206.

［8］DING J，MCCOLL I R，LEEN S B.The application of fretting wear modelling to a spline coupling［J］.Wear，2007，262(9/10):1205-1216.

［9］DING J，SUM W S，SABESAN R，et al.Fretting fatigue predictions in a complex coupling［J］.International Journal of Fatigue，2007，29(7):1229-1244.

［10］DING J，LEEN S B，WILLIAMS E J，et al.Finite element simulation of fretting wear fatigue interaction in spline couplings［J］.Tribology，2008(2):10-24.

［11］MADGE J J，LEEN S B，SHIPWAY P H.The critical role of fretting wear in the analysis of fretting fatigue［J］.Wear，2007，263(1-6 SPEC ISS):542-551.

［12］KAHRAMAN A.A spline joint formulation for drive train torsional dynamic models［J］.Journal of Sound and vibration，2001，241(2):328-336.

［13］CHASE K W，SORENSEN C D，DECAIRES B.Variation analysis of tooth engagement and load sharing in involute splines［C］//American Gear Manufactures Association Fall Technical Meeting 2010.Virginia:American Gear Manufacturers Association，2010:54-55.

［14］胡正根，朱如鹏，靳广虎，等.航空渐开线花键副微动摩擦接触参数分析［J］.中南大学学报:自然科学版，2013，44(5):1822-1828.

［15］李润方，王建军.齿轮系统动力学:振动、冲击、噪声［M］.北京:科学出版社，1997.