基于自动微分与伪谱法的小推力借力轨道设计

张 勃，泮斌峰，唐 硕

(西北工业大学 航天学院，710072西安)

小推力发动机具有比冲高、质量轻的特点，在深空探测任务中，采用小推力发动机能够有效提高探测器有效载荷的比重.在可以预见的未来，小推力发动机将成为深空探测任务中不可或缺的动力系统.但是，由于小推力发动机产生的是很小的连续推力，并且工作时间很长，使得小推力转移轨道会呈现出非常强的非线性［1］，导致传统基于大推力脉冲变轨的轨道设计方法已不能满足需求.而且，由于深空探测器转移轨道必须满足发射时间、飞行时间以及星历等的约束，形成了一个多约束、高度非线性的最优控制问题，使得小推力问题的求解异常复杂.

借力飞行技术也叫引力甩摆或引力辅助轨道转移技术［2］.探测器在进入借力天体的影响球和飞出借力天体的影响球时，其相对借力天体的速度大小不变，仅改变相对速度的方向.但是探测器飞入和飞出行星影响球时相对太阳的速度大小和方向均发生了变化，从而导致探测器脱离借力天体影响球后日心轨道发生改变，达到变轨的目的.借力飞行技术不仅可以节省燃料，而且可以实现对借力天体的观测，提高探测器的利用率.

近年来，由于人类深空探测活动的需要，小推力结合借力飞行的轨道设计方法受到了广泛关注.文献［3］用间接优化的方法对小推力借力轨道的优化设计进行了研究，首先用脉冲轨道转移的方法得到借力序列和切换结构，然后从后向前逐段优化，再将各段拼接起来.为了简化计算，Casalino去掉了借力高度的约束，这样得到的结果不一定能够满足实际任务约束.由于基于庞特里亚金极大值原理的间接优化算法求解过于复杂，限制了它的应用.文献［4］提出的shape based方法采用正弦指数函数来拟合轨道的形状，通过不断调整相关参数，进行初值搜索，这种方法提供了一种有效的初值搜索手段.文献［5-7］用shape based方法对小推力借力轨道的优化设计进行了研究.但是该方法在调整函数中的参数时很困难，需要清晰理解相关参数的物理意义，而且计算规模大，计算成本高［8-9］.文献［8］根据形状法和伪谱法，提出一种混合优化策略对小推力借力轨道进行了研究.文献［9］采用微分进化、拟退火算法与序列二次规划相结合的方法研究了小推力借力轨道的优化问题.文献［10-12］用随机搜索算法与确定性算法相结合的混合方法对小推力借力轨道进行了研究，这些方法中随机搜索算法的收敛速度慢、精度低，影响了算法的性能.文献［13］提出了一种基于形状逼近策略的小推力借力轨道的初始设计方法，但并没有进行更为详尽的优化设计.

本文采用B平面借力模型，建立了小推力借力转移轨道的数学模型.采用高斯伪谱法对整个轨道进行离散，把发射时间和交会条件作为端点约束，借力高度与B平面角作为借力的控制量，并约束在一定范围内，建立起完整的整个转移轨道的离散模型.用SQP方法对离散后的非线性规划问题进行求解.为了提高导数的计算精度，从而加快收敛速度，求解过程中的导数信息通过自动微分获得.由于小推力借力轨道的空间和时间跨度很大，离散后的NLP问题规模非常大，为了使计算快速收敛，本文提出了串行优化和弹性约束的策略.本文方法将发射时间的搜索和飞行轨迹的优化包含在同一计算框架内，避免了传统混合算法中进化算法收敛速度慢的缺点.

1 模型建立

1.1 基本假设

探测器在太阳系内运动时，受到太阳和各个行星引力的作用，是一个多体问题.在对探测器轨道进行精确设计之前，一般忽略次要因素，以二体问题为基础设计轨道的初步方案.同样，探测器进行借力的过程也是一个复杂的过程，在初步方案设计阶段予以简化.本文基于如下简化假设.

1)探测器飞离地球影响球，飞向目标星体的星际航行段仅考虑太阳作为中心天体的引力作用，此段轨道通常为椭圆轨道.探测器进入借力天体影响球内时仅考虑借力天体为中心引力体，其飞行轨迹相对于借力天体为双曲线轨道.

2)由于探测器日心转移飞行时间较长，借力时间可以忽略不计(以金星为例，高度10 000 km的圆轨道周期大约为6.24 h，而整个日心转移时间至少需要上百天)，即将借力飞行看作是瞬时脉冲(无需消耗工质)，借力飞行前后的探测器日心位置没有变化.

1.2 动力学模型

在日心黄道惯性系中，探测器的轨道动力学方程为

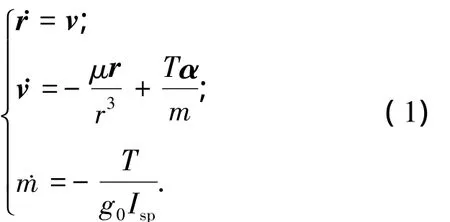
其中:r为探测器的位置矢量;v为速度矢量;μ为太阳引力常数;T为发动机的推力大小;m为探测器质量;α为发动机推力的单位方向矢量;g0为地球重力加速度;Ⅰsp为发动机比冲．为提高计算精度和收敛速度，需要用正则天文单位对动力学方程进行无量纲化，无量纲化后的动力学方程与方程(1)的形式完全相同．

1.3 发动机模型

本文中的探测器采用太阳能电离子发动机.假定太阳能帆板受照面积为常值，则发动机的输入功率P随着探测器日心距离的增大而减小，它与探测器日心距的平方成反比，即

其中P0为探测器日心距离为1 AU时的输入功率，r采用天文单位，发动机推力大小T为

其中η为发动机的工作效率．

1.4 行星借力轨道模型

探测器的行星借力飞行使得整个动力学过程的非线性更强，解空间变得更为复杂.选择合适的借力轨道模型不仅可以简化计算，而且可以获得较高的精度.本文采用B平面模型［14］对借力轨道进行分析，引入了B平面角和借力高度作为控制量，降低了轨道对控制变量的敏感度，提高了轨迹优化设计的鲁棒性.

行星借力B平面示意如图1所示．B平面垂直于探测器飞入行星引力影响球时的双曲线超速矢量v-∞，并且经过飞越行星的引力中心．定义B矢量为B平面与探测器轨道面的交线，由行星引力中心指向探测器方向，记为B;T矢量定义为B平面与日心黄道坐标系的交线，由行星引力中心指向探测器方向，记为T．定义B平面角γ为矢量B与矢量T的夹角．

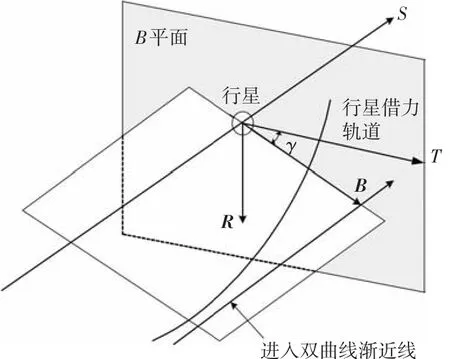
图1 行星借力B平面示意

根据借力飞行的原理，借力前后探测器相对于飞越行星的相对速度大小不变，只改变相对速度矢量的指向，相对速度矢量的方向变化角度由式(6)给出:

其中rp为飞越半径，μp为飞越行星的引力常数．

根据B平面的几何关系，可以得到探测器经行星借力后飞出行星影响球的双曲线超速矢量为

其中

根据上述借力模型，对于给定的借力飞越半径rp和B平面角γ，就可以由探测器进入行星引力影响球时的双曲线超速矢量v-∞计算得到探测器飞出行星引力影响球的双曲线超速矢量v+∞．在借力轨道的设计与优化过程中可以通过调节飞越半径rp和B平面角γ来控制v+∞．

2 轨道优化问题描述

2.1 性能指标函数及约束条件

根据深空探测任务的性质，燃料越省，就意味着更长的使用寿命和更高的有效载荷.因此性能指标取为

其中:t0为从地球发射的时间;tf为到达目标星体的时间;m0为探测器的初始质量．

探测器的发射时间不定，通常被要求在某一时间范围内完成，而探测器到达目标星体的时间亦不定．但是探测器的发射时间和到达时间必须满足星历约束．对于任何发射时间t0，探测器必须满足地球星历约束，即

其中:r，v是发射时刻探测器在日心黄道坐标系中的位置向量和速度向量;rE，vE是此刻地球的位置向量和速度向量;v∞是地球逃逸双曲线速度．本文中v∞=0，即探测器以双曲线超速为零逃逸出地球．

探测器飞越借力星体时，探测器的位置必须满足借力星体的星历约束，即

其中tm为借力时刻，rF为借力行星的位置矢量．

当探测器与目标交会时，探测器的位置与速度必须满足

其中rM，vM分别为目标星体的位置和速度矢量．本文中的星历均采用JPL实验室提供的DE405行星星历［15］.

2.2 最优控制问题

为了便于最优控制问题的描述，令状态变量x(t)=[rvm]T，x(t)∈R7，推力控制量u(t)=α，u(t)∈R3．由式(1)可以得动力学方程的形式为

目标函数(9)记为

在飞行过程中，状态变量必须处于合理的取值区间内，即

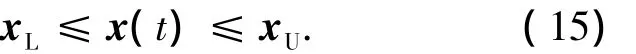
推力的控制变量为单位方向矢量，因此必须满足

探测器发射时刻必须满足地球星历约束(10)，记为

借力控制量飞跃半径rp和B平面角γ的取值必须满足

借力时刻tm，探测器的速度必须满足借力前后的关系(7)，记为

探测器的位置矢量必须满足借力行星星历约束(11)，记为

到达目标星体时必须满足交会要求(12)，记为

最后，总的飞行时间必须限制在可接受的范围内

小推力借力轨道的优化设计问题可以描述为:寻找推力控制量u*(t)∈R3，借力控制量和γ*，使得目标函数J最小，同时满足动力学方程(13)以及约束(15)～(22)．可见小推力借力轨道的优化设计问题是一个高度非线性，多边值约束，具有内点约束并且不连续(速度存在突变)的最优控制问题，导致问题的求解异常复杂．

2.3 俯仰角和偏航角的计算

在前面的动力学模型中，发动机推力的方向矢量定义在日心黄道坐标系中，不便于轨道机动的实施．实际上，发动机推力的方向由探测器轨道坐标系中的两个角度来确定，即俯仰角和偏航角．俯仰角α定义为推力矢量在探测器轨道平面内的投影与当地水平面的夹角，偏航角β定义为推力矢量与探测器轨道平面之间的夹角．俯仰角和偏航角的大小分别由下式给出:

3 高斯伪谱法基本原理及NLP问题求解策略

3.1 高斯伪谱法基本原理

伪谱法是近年提出的一种求解最优控制问题的直接方法，具有收敛半径大、收敛速度快、初值不敏感等特性，在航天航空领域得到了广泛的应用［16-18］.高斯伪谱法在勒让德多项式的零点(即Legendre Gauss点)上对状态变量和控制变量进行离散，以离散点上的状态变量和控制变量构造拉格朗日多项式对连续状态变量和连续控制变量进行逼近，通过对全局差值多项式求导来近似状态变量的导数，从而将微分方程约束转化为一组代数约束.性能指标中的积分项和终端状态由高斯积分得到.经过上述变换，就可将最优控制问题转化为具有一系列代数约束的非线性规划(NLP)问题.

3.2 NLP问题求解策略

在高精度的优化设计中，离散点的数量通常很大，导致求解变量数量也随之剧增，若直接对大规模NLP问题进行求解可能会导致收敛速度非常慢，甚至不能收敛.针对这一问题，本文提出串行优化和弹性约束的求解策略(如图2所示).串行优化有两层含义:1)将优化问题分成若干子段，分段进行优化，以前一段的结果作为后一段的初值，求出每一段各自部分最优解，再将各段优化结果结合起来得到次优解，并作为原优化问题的初始猜想，最终求得整体最优解;2)先以较少的离散点来对轨道进行参数化，求得优化结果;对优化结果进行插值，将优化结果映射到新的计算网格上作为初始猜想，然后逐步增加离散点，提高计算精度.弹性约束指先忽略(或者放宽)某些约束，使得NLP问题能够快速收敛，当离散点逐步增多时增加(或收紧)被忽略(或放宽)的约束，这样逐级进行计算，不断提高精度，最终求得满足约束的精确解.

图2 两种不同意义下的串联优化策略

在进行计算时，不仅两种意义下的串行优化策略可以互相包含，交叉使用，而且串行优化策略可以与弹性约束策略相互耦合.灵活地运用串行优化和弹性约束策略不仅可以增强计算的鲁棒性，而且可以显著加快收敛速度.

3.3 自动微分

采用SQP方法对得到的NLP问题进行求解时，导数的计算精度关系到最终结果的精度以及NLP问题收敛的快慢，导数计算精度不高甚至会导致NLP问题的求解过程不能收敛.常用的导数计算方法一般有解析导数、有限差分和自动微分3种.解析导数只适用于导数所依赖的自变量关系较为简单的情况，当导数所依赖的自变量关系较为复杂时则很难得到解析导数，因此解析导数的适用范围有限.有限差分法是普遍采用的一种数值计算导数的方法，分为前向差分、后向差分以及中心差分，有限差分实现简单，但计算精度不高.自动微分是机械地运用链式求导法则对计算机程序形式的函数求导的一组技术［19］.自动微分的基本思想是无论描述函数的程序多么复杂，其本质都是执行一系列的元代数运算或元函数运算.对这些初等运算迭代地运用链式求导法则，就可以自动、精确地得到目标函数的任意阶导数［20］.

根据链式求导法则累加的方式不同，自动微分分为正向模式和逆向模式.如果从中间变量到独立变量按照程序的执行顺序进行求导称为正向模式;反之，如果从依赖变量到中间变量按照与程序执行顺序相反的方向进行求导称为逆向模式.由于向量函数的求导最终需要转换为标量函数的求导，因此下面以标量函数的求导为例来说明正向模式和逆向模式的实现方式.

考虑函数y=f(x)，f:Rn→R，可以由下面的程序实现:

其中函数fi依赖于已经计算出的xj的值，j∈Ji，Ji⊂{1，2，…，i-1}，i=1，2，…，m，即f由m-n个基本初等函数fi复合而成．基本初等函数fi的导数▽fi=(∂fi/∂xj)j∈Ji可以精确求得．由链式求导法则可以得到正向自动微分的实现方式:

其中ei为R空间中第i个笛卡尔基向量．

为了描述自动微分的逆向模式，记与中间变量xi相关的导数为≡∂xm/∂xi．由定义可以得到1，∂f(x)/∂xi=i，i=1，2，…，n．由链式求导法则可以得到其中Tj≡{i≤m:j∈Ji}，进而得到逆向模式的实现方式:

其中(·)ni=1表示i从1增长到n．当取初始向量=0，γ=1时，计算所得向量g即为梯度▽f．

为提高计算精度和收敛速度，本文采用自动微分计算约束和目标函数的一阶导数，以此提供给SQP方法进行迭代运算.假设离散后的动力学方程在第k个离散点处的状态为Xk，约束向量为Ck，则采用前向自动微分求解约束Ck对Xk的一阶导数可以表示为其中ckm为离散约束向量Ck的元素，xij为离散状态向量Xk的元素．均为基本初等函数的求导．无论ckm的形式多么复杂，经过有限步总能分解为初等函数的导数相乘的形式，而初等函数的导数都具有解析表达式，可以精确求解．把等的导数值相乘即可得到导数的值，进而求得的值．针对配点法(伪谱法属于全局配点法)得到的非线性规划问题，离散点处的约束通常只与当前点的离散状态变量以及离散控制变量相关，因此当前约束对非当前点的离散量的导数为0．所以通过预先的判断，可以避免不必要的微分计算，减小计算量．

目前运用算子重载方法的自动微分软件的典型 代 表 有ADOL-C、ADF、FADBAD/TADIFF、CppAD、ADC和MAD等，基于代码转化方法实现的典型软件包有ADIC、TAPENADE、ADIFOR和OpenAD等.本文采用MAD软件包作为自动微分工具，它是TOMLAB软件中的一个MATLAB工具箱，采用前向自动微分模式.

4 仿真计算与分析

本文以地球-金星-火星交会任务的燃料最省小推力借力转移轨道进行设计.探测器在2021年1月1日到2021年12月31日之间从地球发射，假设出发时刻探测器的日心位置和速度与地球相同(即探测器的地球逃逸速度为零);飞越金星进行借力，借力高度范围为200～10 000 km，最终与火星交会，总飞行时间约束在500 d到1 500 d之间.行星借力模型采用B平面模型，采用高斯伪谱法分别对地球到金星和金星到火星的轨道进行离散化.由于整个轨道的空间和时间跨度很大，为了得到较高的精度就必须采用足够多的配点.整个轨道采用的配点数N=200(地球到金星、金星到火星分别100个配点)，使用基于MTALAB的TOMLAB对NLP问题进行编程求解，导数信息通过MAD用自动微分法进行计算.探测器的主要参数见表1.

表1 探测器主要参数

尽管高斯伪谱法具有较强的鲁棒性，但是由于小推力借力轨道的优化设计非常复杂，如果直接对大规模的NLP问题进行求解会导致收敛速度比较慢，甚至不能收敛，因此本文采用前面所述的串行优化和弹性约束策略.首先将轨迹优化问题分解为地球到金星和金星到火星的小推力轨道转移问题，求出次优解;然后以次优解作为初始猜想，分别采用不同的高斯点进行串联求解，即以较少离散点的优化结果作为下一步优化的初始猜想，逐级进行优化.表2给出了不同串联级数的优化耗时，当配点数N=20、40、60时不考虑借力高度约束，N=80、100、200时增加对借力高度的约束，使NLP问题能够很快收敛.

可以看到，随着串联级数的增加，总的优化耗时逐渐减少，但是在一定串联级数之后优化耗时随串联级数的增加不再明显减少，这是由于一定串联级数之后优化结果已经接近最终优化结果.N=200时离散变量个数达到了2 019个，约束为1 618个，对于如此大规模的NLP问题，通过串联优化仍然能够快速收敛，精确得到了满足上述约束条件的小推力借力轨道，证明了本文求解策略的有效性.主要优化结果见表3.

表2 不同串联优化级数求解耗时对比

表3 小推力借力轨道优化结果

导数信息的计算精度对依赖于导数信息的NLP问题求解方法的收敛速度有很大影响，精度越高，收敛速度越快.为了排除实现语言和实现方式对计算时间的影响，以约束函数(目标函数过于简单，无比较意义)的计算次数和约束雅可比矩阵的计算次数作为指标对自动微分方法和差分方法对优化过程的影响进行了比对，如表4所示，结果显示自动微分方法能够明显加快优化的收敛速度.

表4 自动微分与差分方法计算导数对优化过程的影响对比

图3给出了探测器的整个飞行轨迹，可以看到优化结果很好地满足了借力和交会条件，验证了本文算法的正确性.图4为飞行轨迹在x-y平面的投影，清晰地反映了轨迹与各行星之间的关系.

图3 探测器三维轨迹

图4 探测器轨迹在x-y平面的投影

图5为探测器日心距和速度的变化历程，其中探测器的速度在进行借力后存在突变，这是由于B平面模型没有考虑借力的过程，认为借力是在某一点瞬时完成的．由于B平面模型并不影响探测器的位置，因此探测器的日心距不存在突变．

图5 探测器日心距与速度时间历程

图6给出了控制角的变化历程.同样也是由于B平面模型的原因，俯仰角与偏航角都存在突变.借力前，俯仰角单调增加，但始终为负值，这是因为金星轨道半径小于地球轨道半径，探测器必须不断减小日心距.而借力后由于火星轨道半径大于金星轨道半径，探测器首先需要增加日心距，当达到火星轨道附近时为了满足与火星交会的要求，探测器需再对控制角进行调整.偏航角的变化幅值较小，这是因为金星、地球和火星轨道的轨道倾角相差不大，轨道面之间的调整所需控制力较小.

图6 控制角时间历程

5 结语

本文基于自动微分和高斯伪谱法研究了小推力借力轨道的优化设计问题，将发射时间的搜索与轨道的设计包含在了同一计算框架内，避免传统混合方法中随机搜索算法收敛速度慢、精度低的缺点.为了增强算法的鲁棒性、加快收敛速度，本文提出了串联优化策略和弹性约束策略.针对有限差分法求解导数信息精度有限而解析导数又难以获得的问题，本文采用自动微分的方法求解导数信息，保证了导数计算的高精度和快速收敛.通过地球-金星-火星小推力借力轨道的仿真验证，证明了本文算法的正确性和有效性，为未来深空探测轨道优化提供了有益的参考.

［1］BETTS J T.Very low-thrust trajectory optimization using a direct SQP method［J］.Journal of Computational and Applied Mathematics，2000，120(1):27-40.

［2］张旭辉，刘竹生.火星探测无动力借力飞行轨道研究［J］.宇航学报，2008，29(6):1739-1746.

［3］CASALINO L，COLASURDO G，SENTINELLA M R.Low-thrust trajectories to mercury with multiple gravity assists［C］//43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference＆Exhibit.Cincinnati，OH:［s.n.］，2007.

［4］PETROPOULOS A E.A shape-based approach to automated，low-thrust，gravity-assist trajectory design［D］.West Lafayette:Purdue University，2001.

［5］MCCONAGHY T T，DEBBAN T J，PETROPOULOS A E，etal.Design and optimization of low-thrust trajectories with gravity assists［J］.Journal of Spacecraft and Rockets，2003，40(3):380-387.

［6］YAM C H，MCCONAGHY T T，CHEN K J，et al.Preliminary design of nuclear electric propulsion missions to the outer planets［C］//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Providence，Rhode Island:［s.n.］，2004.

［7］PETROPOULOS A E，LONGUSKI J M，FGLIO E P B.Trajectories to jupiter via gravity assists from Venus，Earth，and Mars［J］.Journal of Spacecraft and Rockets，2000，37(6):776-783.

［8］李小玉，郑建华.基于形状法和伪谱法的小推力借力优化研究［J］.计算机仿真，2013，30(1):100-103.

［9］赵遵辉，尚海滨，崔平远.基于混合优化方法的小推力借力转移轨道设计与优化［C］//第30届控制年会.烟台:［s.n.］，2007.

［10］WOO B，COVERSTONE V L，CUPOLES M.Lowthrust trajectory optimization procedure for gravity-assist，outer-planet missions［J］.Journal of Spacecraft and Rockets，2006，43(1):121-129.

［11］de PASCALE P，VASILE M.Preliminary design of lowthrust multiple gravity-assist trajectories［J］.Journal of Spacecraft and Rockets，2006，43(5):1065-1076.

［12］CARNELLI I，DACHWALD B，VASILE M.Evolutionary neurocontrol a novel method for low-thrust gravity-assist trajectory optimization［J］.JournalofGuidance，Control，and Dynamics，2009，32(2):612-624.

［13］尚海滨，崔平远，徐瑞，等.结合行星借力飞行技术的小推力转移轨道初始设计［J］.宇航学报，2011，

32(1):29-37.

［14］MCCONAGHY T T.Design and optimization of interplanetary spacecraft trajectories［D］.West Lafayette:Purdue University，2004.

［15］CURTIS H D.Orbital mechanics for engineering students［M］.Oxford:Butterworth-Heinemann，2005.

［16］BENSON D.A gauss pseudospectral transcription for optimal control［D］.Cambridge:Massachusetts Institute of Technology，2005.

［17］杨希祥，张为华.基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究［J］.宇航学报，2011，32(1):15-21.

［18］宗群，田柏苓，窦立谦.基于Gauss伪谱法的临近空间飞行器上升段轨迹优化［J］.宇航学报，2010，31(7):1775-1781.

［19］李翔.基于自动微分算法的过程系统优化［D］.杭州:浙江大学，2003.

［20］蒋占四，吴义忠，蒋慧.敏度分析的数值方法比较研究［J］.计算机与数字工程，2009，37(5):1-5.