挠性系统谐振频率摄动范围的几何解法

王永坤，孙明玮，刘忠信，陈增强

(南开大学 自动化系，300071天津)

存在挠性结构或包含挠性部件的一类系统称为挠性系统.挠性系统中的挠性部件分为很多种，例如卫星的太阳能帆板［1-3］、机器人的机械臂［4］、大型运载火箭或具有一定范围长细比的有翼飞行器等.此类系统的一个主要特点是系统中存在弱阻尼的谐振模态，在控制系统设计时需要特殊考虑，以保证闭环系统稳定［5］.挠性系统振动模态谐振频率的理想值或者是通过理论方法计算出来的，或者是通过地面振动试验测量出来的.理论计算中分布质量和结构特性存在的误差，地面试验中空天的不一致性以及测量误差等，都会导致谐振频率误差.飞行器在飞行过程中，振动模态的一些特征参数会随着温度和质量的变化而变化，因此通过理论计算或者模态振动试验得到的谐振频率具有一定的不确定性，在控制系统的设计过程中必须考虑其对于闭环鲁棒稳定性的影响.文献［6-7］指出采用H∞回路成形法［8-10］设计挠性控制系统时，由于系统中弱阻尼模态的存在，会减小谐振频率的实际摄动范围，并不能保证系统具有期望的鲁棒性，但是并没有给出计算谐振频率实际摄动范围的方法，同时文献［7］计算出的系统H∞范数的逆并不代表系统中谐振频率摄动值的百分比，它实际是系统综合摄动范围的一个指标.由于谐振频率分别出现在一次项和二次项中，导致其非线性的耦合摄动形式，传统的线性或双线性分析方法不再适用［11-12］.目前还没有发现文献报道存在系统性的计算方法可以直接确定挠性系统谐振频率的摄动范围.针对这个问题，工程上只能采用摄动试验法，通过试凑的方式摸索得到谐振频率的稳定性边界，该方法不仅费时费力，而且精度难以得到保证.因此，本文给出一种基于D分割法［13］的系统鲁棒稳定性分析方法，给出弱阻尼模态下谐振频率摄动范围的几何求法，并通过一个算例验证了该方法的有效性，同时通过另一算例说明了本方法可直接推广应用到具有多个模态的挠性系统分析中.

1 问题描述

本文以具有太阳能帆板的卫星为例来分析挠性系统谐振频率的摄动范围，但文中方法也可直接推广到有翼飞行器等挠性对象的分析中.一般来说，挠性结构振动具有无穷多个模态，但是振动能量主要集中在低阶项上，因此挠性系统设计时常以一阶模态为主，将高阶模态作为未建模动态来处理.在控制系统设计时要求控制器的增益在一阶模态频率后迅速衰减.图1给出了卫星示意图.在图1(a)中，θ1是卫星主体与星体的夹角，θ2是卫星姿态角，代表星体传感器与仪表设备的夹角，图1(b)所示为将传感器安装到与θ2相连的圆盘上的卫星等效机械系统图.对图1所示模型，假设用弹簧链接的两个质体的扭矩常数为k，粘性阻尼系数为b，建立线性模型如下［4］:

其中Tc为作用在主体上的控制力矩，J1、J2分别是图1(b)中两个质体的转动惯量．由式(1)可得含有一维振动模态的挠性系统模型为

其中

式中c0、c1是模态幅值，只考虑一阶模态时c0=-c1，ωn和ξ分别是系统的谐振频率和阻尼比．在卫星飞行过程中，参数k会随温度的波动以及外形结构特性而变化，因此由式(3)可知谐振频率ωn会发生摄动．从式(2)可以看出ωn分别出现在一次项和二次项中，导致其摄动形式是非线性的，其对于闭环控制系统的影响不是简单的线性或者双线性形式，传统的分析方法无法直接应用［11-12］．

图1 卫星及其双体

2 基于D分割法的鲁棒稳定性分析

2.1 D分割法

考虑如下一类反馈控制系统的闭环特征多项式:

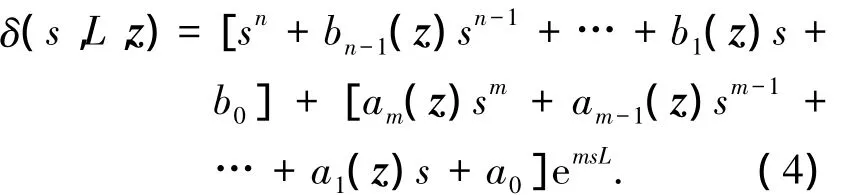
其中ak(z)和bk(z)分别为参数向量z的连续函数，z=［z1，z2，…，zl］Τ．L为系统的时滞常数，L∈Η⊂R，zi∈Q⊂RL，R为实数集．

对于给定l阶向量z和L，若特征多项式δ(s，L，z)无非负实部零点，则称其渐近稳定．由于δ(s，L，z)的零点为z和L的连续函数，空间Η×Q被超曲面分割成若干个区域，超曲面上的点对应的δ(s，L，z)至少有一个纯虚根或s=∞，这种分解法称为Η×Q的D分割法．D分割法的实质是将s平面上的虚轴映射为参数空间Η×Q的超曲面，根据实数根穿越原点和穿越无穷，复根穿越虚轴得出D分割边界［14］．

其中

显然，随着z和L的连续变化，稳定系统变化到不稳定系统中间必然穿越∂D．换句话说，研究鲁棒稳定边界只需要通过分析∂D就可以实现．

2.2 一维线性不确定系统的鲁棒稳定性分析

由于本文所研究问题的时滞特性可以忽略，因此考虑如下特征多项式:

其中ai(i=0，1，…，n)是多项式系数，假设ai(i=0，1，…，n)均可由特定参数d的线性函数表示，d是式(5)中的不确定参数，则上式可写为

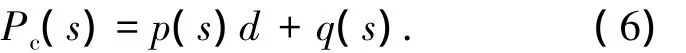
其中p(s)和q(s)是两个互质的多项式．假设当式(6)中的d=0时，Pc(s)是稳定的．

此时，基于D分割法，鲁棒稳定边界∂D上的p(s)和q(s)分别是

其中f(ω)、e(ω)、h(ω)、g(ω)均为实数多项式．由Pc(jω)=0有

消去上式中d，可得

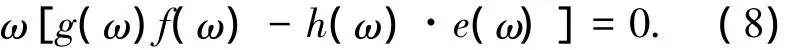
求解式(8)得到的正实根ωi，表示系统的截止频率．将ωi代入式(7)可得

定义

其中d+，d-即为在满足系统鲁棒稳定前提下，不确定参数d的正负摄动边界．

2.3 二维线性不确定系统的鲁棒稳定性分析

当式(5)的某些系数中存在d1，d2两个不确定参数，并且这些系数均可表示为d1，d2的双线性函数形式时，就成为一个二维线性不确定问题．假设当d1=d2=0时，Pc(s)是稳定的．为了确定d1、d2的鲁棒稳定区域，首先，令d2=0，采用2.2节的方法求得此时参数d1的鲁棒稳定区域为然后，在区域内均匀采样N个点，对于其中每一个d1，i(i=1，2，…，N)，求解此时关于不确定参数d2的鲁棒稳定区域;最后，分别连接点和和其中i=1，2，…，N-1，不确定参数的鲁棒稳定区域如图2阴影部分所示．对于多维线性不确定系统，其鲁棒性分析方法类似．对于存在二维或者多维不确定参数的系统，当各个不确定参数之间存在一定的关系，而参数之间的关系曲线与上述得到的鲁棒稳定区域的交点即为各个参数的摄动边界．而摄动点一般在摄动边界内选取是有意义的．

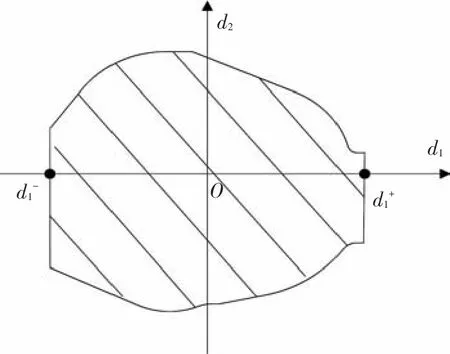
图2 不确定参数鲁棒稳定区域示意图

2.4 挠性系统的鲁棒稳定性分析

考虑式(2)所表示的挠性系统，系统的闭环特征多项式为

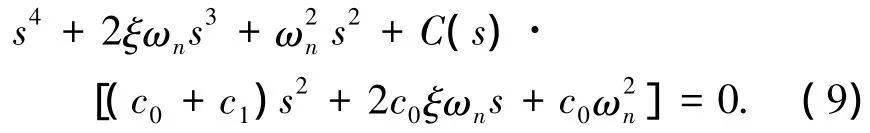
其中C(s)是控制器，谐振频率ωn是摄动因子，分别出现在一次项和二次项中．

现在考虑一个更广义的二维不确定性系统．将式(9)中ωn的一次项和二次项分别表示为

其中ωn和ωn2分别表示谐振频率摄动后的一次项和二次项，n是谐振频率的标称值，d1和d2分别表示摄动的百分比，此时存在d1和d2两个不确定参数，转化为二维不确定性问题．采用2.3节的方法，假设在给定n、ξ、c0、c1和C(s)的情况下，绘制出不确定参数鲁棒稳定区域即图3中的阴影部分．

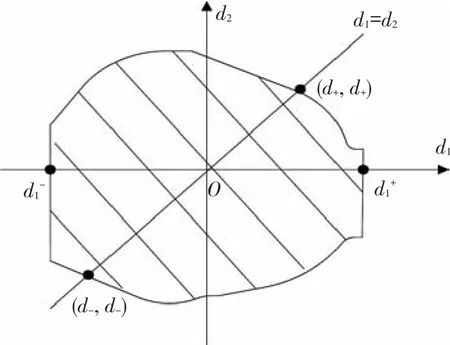
图3 鲁棒稳定参数区域

对于包含二阶振动模态的挠性系统，即存在ωn1和ωn2两个不确定参数．首先令ωn2固定为标称值，通过上述方法求得ωn1的摄动区间．然后在ωn1的摄动区间内均匀采样，对于每一个采样值，可以求出ωn2的摄动边界值，最终得到［ωn1，ωn2］的整体摄动区域．对于包含多阶振动模态的挠性系统，分析方法类似．

3 算 例

例1 考虑具有两个太阳能帆板的卫星模型［7］，其中c0=1.731 9×10-5，c1=3.785 9×10-4，ωn1=1.539 rad/s，ξ1=0.003，此类系统具有明显的挠性，一阶模态的c1大于刚性模态的c0．

这里直接引用文献［7］中的控制器设计结果，通过回路成形法得到H∞控制器．首先给被控对象加入串联补偿环节，使其具有期望的开环特性，即回路成形．然后针对补偿后的广义对象，设计H∞控制器，保证闭环系统的稳定性．其中补偿函数选择为

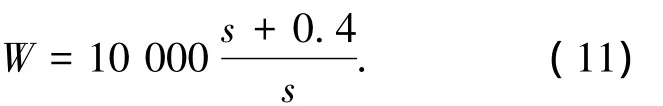
由式(2)、(10)和(11)可得广义的系统传递函数为

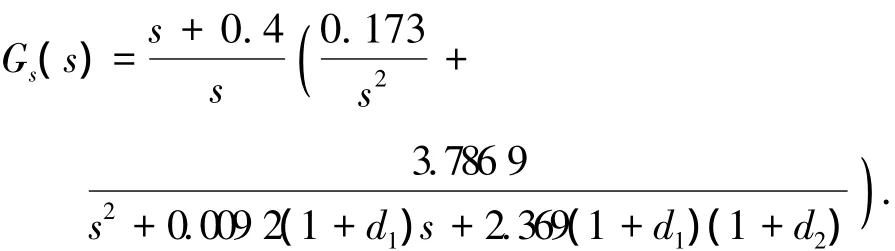
当d1=d2=0时，针对标称系统设计的H∞控制器为

因此可得闭环特征多项式

令d2=0，根据2.2节一维不确定参数分析方法可以计算出，d1的允许摄动区间为［-0.611 4，0.312 3］．由于直线d1=d2只通过第一、三象限，因此针对每一个采样的d1，i;当d1，i≥0时，只需求出此时对应的d2摄动的上边界值当d1，i＜0时，只需求出此时对应的d2摄动的下边界值，结果如图4所示．直线d1=d2与一、三象限边界的交点分别为(0.138 6，0.138 6)和(-0.351 4，-0.351 4)，表明谐振频率ωn1增加13.86%或减小35.14%后，系统处于临界稳定状态，ωn1的摄动范围即为［-35.14%，13.86%］．

图4 谐振频率ωn1的摄动范围

摄动系统的阶跃响应曲线如图5所示，其中实线表示标称系统的响应曲线，短虚线和长虚线分别代表谐振频率摄动-35.14%和13.86%时的响应曲线．可以看出当ωn1的摄动达到所求的正负边界时，系统出现等幅振荡，验证了本文提出方法的正确性．

图5 系统的阶跃响应曲线

而采用文献［7］的分析方法，求得系统的H∞范数γ=2.486，则γ-1≈0.402 3，根据小增益定理可得只要对象的摄动小于40.23%，就可以保证闭环鲁棒稳定．而实际情况是当谐振频率正摄动14%时就达到了稳定边界，文献［7］得出的结论是:此情况的出现是由于对象存在弱阻尼模态，压缩了实际允许的摄动范围，因此导致H∞回路成形法设计的系统并不一定具有鲁棒性．

本文经过分析，γ-1≈0.402 3表示当系统中的不确定参数ωn1摄动值达到最大时，对应整体不确定项的H∞范数为0.402 3．定义

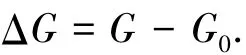
其中G和G0分别表示实际对象和标称对象，ΔG表示对象的整体不确定项，其H∞范数与Δωn1的关系如图6所示，其中横坐标表示谐振频率的摄动值，纵坐标表示‖ΔG‖∞．从图中可以看出当谐振频率ωn1摄动达到正向边界即13.86%时，‖ΔG‖∞为0.407 5，几乎等于文献［7］给出的0.402 3．因此，系统H∞范数的逆并不表示某一参数的摄动范围，而是一种结构参数摄动引起的非结构不确定性变化范围，二者本质上是不同的．

图6 整体不确定项的H∞范数

例2 仍采用算例1的模型以及控制器设计结果，并在此基础上加入一个二阶振动模态，得到如下包含两个振动模态的挠性系统:

其中c0、c1、ωn1、ξ1保持例1中的数值不变，c2=1.02×10-4，ωn2=5.2，ξ2=0.002，谐振频率ωn1和ωn2是系统中的不确定参数．

首先令ωn2固定为标称值，对ωn1进行摄动分析．通过本文提出的方法可得ωn1的摄动比例为d1∈［-0.36，0.163］．对比例1可见，由于二阶模态的能量比较低，对于一阶模态振动频率的摄动范围影响不是很大，因此一般在对挠性系统进行分析时，通常只需考虑能量较大的低阶振动模态即可．当ωn1的摄动达到临界值时，系统的阶跃响应曲线如图7所示出现等幅振荡．

在区间［-0.36，0.163］内均匀采样，对于每一个对应的ωn1值，求得ωn2摄动比例的边界值，最终可得ωn1、ωn2的摄动鲁棒稳定区域，即图8中曲线与坐标轴所围区域，曲线表示摄动的边界．需要说明的是二阶模态谐振频率ωn2的摄动没有上界，反映了谐振频率越高对于整个刚体的影响越小，符合实际经验．在求得区域选取内点(-0.2，-0.5)，阶跃响应如图9(a)所示，可以看出此时系统处于收敛的趋势;在边界上选取(-0.32，-0.713)和(0.07，-0.793)，阶跃响应如图9(b)所示，输出产生等幅振荡.

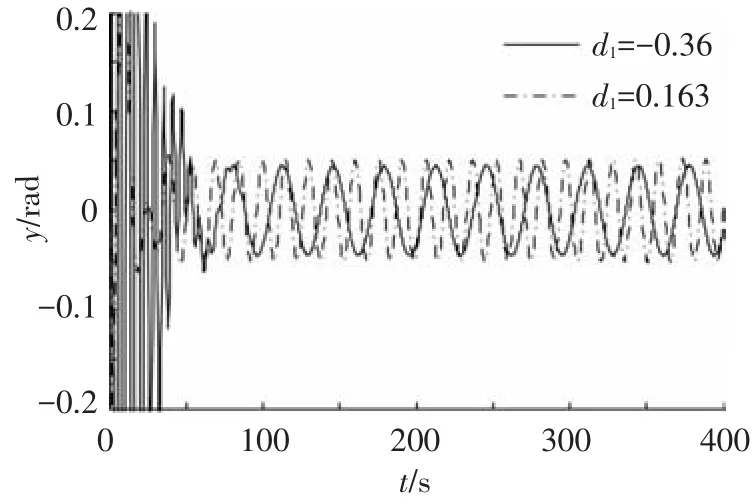
图7 ωn 摄动时系统的阶跃响应曲线

图8 谐振频率ωn1、ωn2的摄动鲁棒稳定范围

图9 ωn1、ωn2摄动时系统的阶跃响应曲线

4 结 语

本文针对挠性系统中不确定谐振频率的鲁棒稳定性分析问题，设计了一种基于D分割法的几何分析方法，给出了振动模态谐振频率的精确摄动范围.通过数值算例验证了该方法的有效性，对于实际工程具有一定参考价值.该方法由于突破了传统鲁棒稳定性分析要求摄动参数必须是线性或者双线性的形式限制，也可推广到其他含参数非线性摄动形式的场合，通过绘制相应的几何曲线求取特定参数的鲁棒稳定性范围.

［1］MCFARLANE D C，GLOVER K.Robust controller design using normalized coprime factor plant descriptions［M］.New York:Springer Verlag，1990:205-208.

［2］刘暾，杨大明.挠性卫星动力学及姿态控制模型的建立［J］.哈尔滨工业大学学报，1985，17(A8):1-17.

［3］崔乃刚，刘家夫，荣思远.柔性太阳帆航天器动力学建模与姿态控制［J］.哈尔滨工业大学学报，2011，43(7):1-5.

［4］FRANKLIN G F，POWELL J D，ABBAS E N.Feedback control of dynamic systems［M］.4th Ed.Reading，MA:Addison-Wesley，1986:488-491.

［5］游江，赵国良，罗耀华.H∞混合灵敏度的鲁棒性设计及在挠性系统控制中的应用［J］.仪器仪表学报，2006，27(6):556-558.

［6］何朕，孟范伟，刘伟，等.H∞回路成形设计的鲁棒性［J］.自动化学报，2010，36(6):890-893.

［7］何朕，孟范伟，王广雄，等.挠性系统的控制设计和H∞回路成形法［J］.控制理论与应用，2013，30(8):1014-1020.

［8］MCFARLANE D C，GLOVER K.A loop shaping design procedure usingH∞synthesis［J］.IEEE Transactions on Automatic Control，1992，37(6):759-769.

［9］KAITWANIDVILAI S，OLRANTHICHACHAT P.Robust loop shaping—fuzzy gain scheduling control of a servopneumatic system using particle swarm optimization approach［J］.Mechatronics，2011，21(1):11-21.

［10］OSINUGA M，PATRA S，LANZON A.Smooth weight optimization inH∞loop-shaping design［J］.Systems＆Control Letters，2010，59(11):663-670.

［11］WEDELL E，CHUANG C H，WIE B.Stability robustness margin computation for structured realparameter perturbations［J］.Journal of Guidance，Control，and Dynamics，1991，14(3):607-614.

［12］WIE B，LU J B.Two real critical constraints for real parametermargin computation ［J］. Journal of Guidance，Control，and Guidance，1994，17(3):561-569.

［13］GRYAZINA E N，POLYAK B T.Stability regions in the parameterspace:D-decomposition revisited［J］.Automatica，2006，42(1):13-26.

［14］GRYZINA E N.The D-decomposition theory［J］.Automation and Remote Control，2004，65(12):1872-1884.