大容量液流电池系统数学模型与仿真

王亚光，王秋源，陆继明，毛承雄，王 丹，杨 赟

（华中科技大学 强电磁与新技术国家重点实验室，湖北 武汉 430074）

0 引言

近年来，随着矿石资源日益匮乏和环境问题日趋严峻，可再生能源发电技术得到了飞速发展。储能系统为大规模风电、光伏等可再生能源平稳接入电网提供了有力支撑[1]。大容量液流电池系统LCFBS（Large Capacity Flow Battery System）作为一种新型储能电池，在储能容量、能量密度、功率密度、响应速度、环保等各方面的综合性能较好[2-3]。LCFBS由多个较小容量的液流电池串并联而成，它们之间不仅存在电极的电路连接，且存在循环电解液的互通，与锂电池、铅蓄电池的串并联有较大差异。对不同串并联方式组成的LCFBS参数的估算与预测更困难[4]。因此，研究LCFBS的准确建模以有效预测其性能参数，对其在实际应用中优化、设计及控制至关重要。

目前，电池单体建模可以分为电化学模型、数学模型和电气模型。电化学模型可以反映电池内部反应机理及相关电池设计参数，用于优化电池结构设计，但其较依赖相关化学参数，模型复杂，非线性方程较多，不适用针对电池外部特性的研究[5]；电气模型使用电压源、电阻、电容组成电路，模拟电池的动态模型，直观方便，适合相应仿真试验，但电池原型数据难以获得，模型精度往往不高；而数学模型通过经验公式和数学拟合的方法得到相应的公式，能够很好地预测电池的相关外特性，但因其状态量较为抽象，对电池电气性能参数表征不直观[6]。

对于LCFBS的建模，文献[7]建立了液流电池的电化学模型和机械模型，但文章的核心是围绕电池特性与钒液流量的关系来展开；文献[8]建立了液流电池的电路模型并搭建了仿真模型，但忽略了电解液流动对电池特性的影响，模型精度不高；文献[9]对液流电池系统的特殊性进行了分析，对电池支路进行了建模和仿真，验证了精确建立液流电池系统模型的必要性，但对其他性能参数预测意义比较局限；文献[10-11]提出了利用数学表达式对光伏电池阵列输出特性进行建模；文献[12-13]通过复杂的数学回归算法确定了锂电池端电压与SOC较为准确的预测方法，但数学表达式过于复杂，且没有分析其模型精度。

本文以大连物理化学研究所研制的100 kW全钒液流电池为原型，利用其原始测试数据，结合LCFBS的电气模型分析，构建其数学模型，并利用多项式进行拟合，最后通过仿真验证了模型的准确性。

1 LCFBS的等效电路模型

1.1 液流电池的工作原理

液流电池的概念最早是由ThallerIn于1974年提出[14]。 1984年，新南威尔士大学的 Maria Skyllas-Kazacos等提出了全钒液流电池原理。如图1所示，全钒液流电池采用V2+/V3+和V4+/V5+进行氧化还原反应。采用不同价态的钒离子溶液作为正负极活性物质，通过外接泵使液态的活性物质不断循环流经电池电堆（battery stack）的内电极，使其发生氧化还原的电化学反应，从而完成化学能到电能的转换。

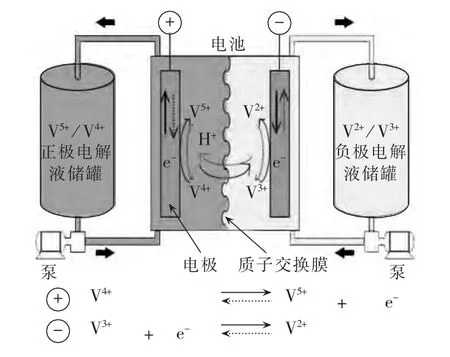
图1 全钒氧化还原液流电池原理图Fig.1 Schematic diagram of vanadium redox flow battery

如图2所示，LCFBS均由某一额定功率的电堆和电解液两部分构成，并通过不同的成组方式串并联以满足其功率和电压等级需求，串联级数记为S，并联级数记为P[12]。每个电堆由n节电池单体（cell）串联并封装而成。其与锂电池、蓄电池等储能系统的不同之处在于，LCFBS的电解液在电堆之间相互连接的管道中循环流动，导致LCFBS有着明显的旁路效应。

图2 大容量液流电池系统结构图Fig.2 Structural diagram of LCFBS

1.2 液流电池等效电路

现有的众多电池等效电路模型中，Thevenin模型能比较准确地反映电池的各方面性能，同时也便于进行相应的理论分析。因此，本文先基于Thevenin电池模型来进行分析。

该模型通过理想电压源U0来描述电池开路电压，用 1 个串联电阻（Rl）和 1 个 RC 并联网络（Rs和 Cs）来预测电池在某一荷电状态SOC（State Of Charge）下对瞬时负载的响应。

本文构建电池模型主要是为了分析其在带载状态下的外特性，暂不考虑其自放电特性，故忽略寄生损耗R0的影响。对图3所示的等效电路进行简化，得到如图4所示的电池等效电路模型。

图3 Thevenin模型Fig.3 Thevenin model of battery

图4 全钒液流电池等效电路模型Fig.4 Equivalent circuit model of vanadium flow battery

该模型结构基本能够描述出电池在充放电过程中的U-I等电池外特性，其中U0、Rl、Rs和 Cs与串联级数、并联级数、SOC以及温度等因素有关。

2 LCFBS数学模型及参数整定

2.1 液流电池单体的基本数学模型

电池随着电解质的扩散进行充放电动作，根据菲克定律得到电化学扩散模型，方程如下[15-16]：

其中，C（x，t）为t时刻距离电极 x处的离子浓度；J（x，t）为 t时刻距离电极 x处的离子流量；D 为扩散系数（m2/s）。

根据式（1）、（2），某个给定电池在 t时刻消耗的总电量可表示为：

其中，Ec（t）为总的电量；Es（t）为剩余的电量。 Es（t）可表示为：

其中，I（t）为消耗电流；β为电池恢复特征值。此时有：

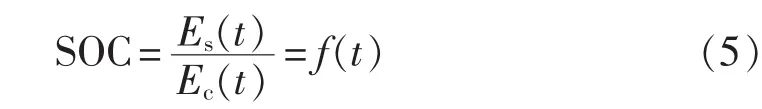
参照图4中等效电路模型，根据式（1）—（5）可推导出：

其中，ai、bi、ci（i=1，2，3）均为电池模型参数[15]。 此模型从数学的角度较为准确地表示了等效电路中的内阻公式。而考虑表达形式的统一且便于计算，同时自然指数ekx又可用关于x的高次多项式逼近，故本文利用式（9）—（11）的形式表达，式中 n为自然数，可以根据拟合精度而设定。通过具体的实验数据拟合得到相应的系数 d0、d1、…、dn（e0、e1、…、en和 f0、f1、…、fn）。

上文为液流电池单体的数学模型分析。本文主要考察电池的外特性，研究的核心参数为内阻、电动势和SOC，暂不考虑电容的影响，因而在分析电池内阻的时候可以将其等效为一个电阻R。

2.2 LCFBS内阻数学表达

LCFBS由多个电堆串、并联而成，其系统结构如图2所示。与其他类型的电池（锂电池等）不同的地方在于：LCFBS在进行充放电反应时，电解液会在不同的电堆之间交叉流动，旁路效应非常明显，导致电池系统的实际内阻值相比较于根据串并联电路理论计算所得的内阻值会出现较大的偏差[9]，不能单纯利用串并联关系将单体情况下的相应数学表示拓展至LCFBS情况。

在对LCFBS进行仿真时，因旁路效应的影响，LCFBS仿真精度随级联规模的扩大而降低。而本文对LCFBS内阻值的分析是基于液流电池系统原型试验数据，通过数学拟合找出串并联对模型参数的影响规律，从而能够比较准确地跟踪实际LCFBS的相关外特性。

2.2.1 单电堆内阻

图5给出了100 kW液流电池系统的组成单元10 kW电堆内阻与SOC的关系。下文以100 kW液流电池系统为研究对象，故单电堆的拟合也以10 kW电堆为主，其拟合函数为：R=f0（SOC）。

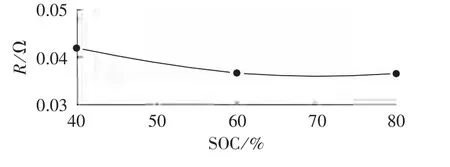
图5 单电堆内阻随SOC的变化趋势Fig.5 Curve of internal resistance vs.SOC for single cell-stack

表1为在不同SOC下单电堆内阻情况。因采用指数函数不太方便，而自然指数ekx可以用0，1，2，…）来表征，结合式（9）—（11），将单电堆的内阻用多项式（12）来表示。

表1 单电堆内阻与SOC的关系Table 1 Relationship between internal resistance of single cell-stack and SOC

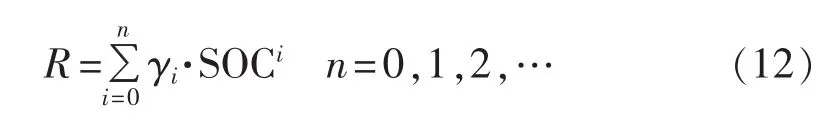
以10 kW电堆的数据为例，根据曲线走势拟合维度n取3，可以较为精确地拟合得到一组参数：

2.2.2 多电堆系统内阻

LCFBS由多个电堆串并联时，内阻的变化规律较为复杂，采用多元高次多项式拟合的方法更为高效、简洁。以二元高次多项式拟合为例，拟合方程可写为：

其中，x、y为多项式方程自变量；Pij为多项式系数；m、n为自然数。按照每个自变量从高至低次数的顺序求和。类似地，可以得到多元（三元及以上）高次多项式的拟合方程。

图6为不同容量电池的内阻随SOC变化的曲线图，可见电池的内阻与串联数S、并联数P和SOC均有关，令内阻的拟合公式为 R=f（SOC，S，P）。

图6 不同容量电池的内阻随SOC变化趋势（电池原始数据）Fig.6 Curve of internal resistance vs.SOC for different battery capacities（original data）

表2为内阻 R与 S、P、SOC的对应关系数据（SOC1、SOC2、SOC3分别取 0.4、0.6、0.8，下文类似）。

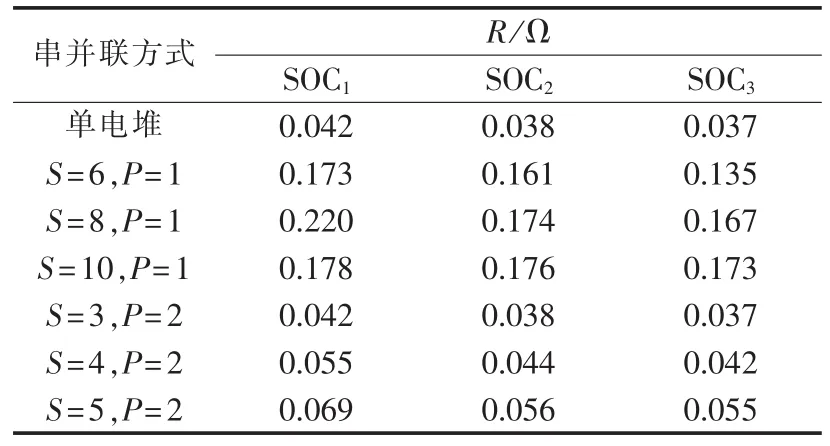
表2 内阻与S、P、SOC的关系Table 2 Relationship between internal resistance and SOCs for different configuration modes（S，P）

利用多项式分段表示，可得到内阻表达式。

当P=1时：

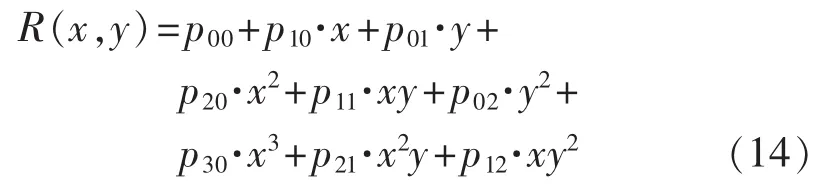
当P=2时：

其中，x、y分别代表SOC、S。根据表2中的电池原始数据可以拟合得到一组模型参数如表3所示，其置信区间取为95%。

通过以上方法拟合得到的三维图如图7所示。图中，z轴代表R，x轴代表SOC，y轴代表S，三维图直观地展示了内阻与串联级数、SOC的关系。

表3 内阻公式参数Table 3 Parameters of internal resistance formula

图7 内阻拟合三维图Fig.7 Three-dimensional charts of internal resistance fitting

2.2.3 拟合优度检验

本文以决定系数λR-square判断多元高次回归模型的可信度。其计算表达式为：

其中，SSR（Sum of Squares of the Regression）为预测数据与原始数据平均值之差的平方和；SST（Total Sum of Squares）为原始数据和原始数据均值之差的平方和。决定系数λR-square是通过数据的变化来表征一个拟合的好坏，其正常取值范围为[0，1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的可信度也较好。此外，以误差平方和SSE表示残差大小，以标准差RMSE衡量离散点离散程度，故得到拟合优度指标如表4所示。

同时，根据以上参数得到的公式计算所得离散点的值与实测值的相对误差分析如表5、表6所示。分析相对误差数据，当P=1时，曲线中数据跳跃相对较大，拟合得到的模型误差偏大，从表4中也可看出此时决定系数稍低；当P=2时，曲线较为平稳，数据拟合导致的误差较小。

表4 拟合优度指标Table 4 Goodness of fit

表5 并联级数为1时内阻相对误差Table 5 Relative errors of internal resistance when P=1

表6 并联级数为2时内阻相对误差Table 6 Relative errors of internal resistance when P=2

总体上，拟合优度各项指标均较好，实测点相对误差在可接受范围内，说明利用高次多项式拟合得到的液流电池内阻表达式精度较高，建模结果可靠。

2.2.4 LCFBS内阻温度修正

上节中暂未考虑温度效应，这是因为试验环境温度为20℃左右时，内阻变化不大。实际情况中考虑温度对内阻影响时，仅需在上述所拟合出的R基础上乘以温度系数KT，即考虑温度效应修正的内阻值为RT=KTR。

图8为电池内阻随温度变化的曲线。

图8 内阻随温度变化趋势（电池原始数据）Fig.8 Curve of internal resistance vs.temperature（original data）

以20℃时内阻为基准值，得到其他各点KT的标幺值，最终拟合出温度修正系数为：

其中，T为热力学温度，单位K。

2.3 LCFBS电动势数学表达

根据化学Nernst方程可得：

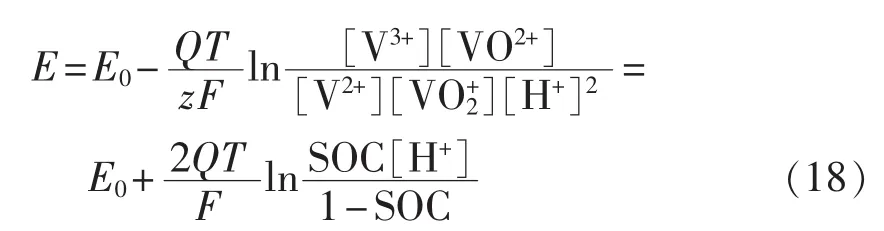
其中，E0为钒电池标准状态下的平衡电势，E0=1.25V；E 为电池单体开路电压；[V3+]、[VO2+]、[V2+]、[VO+2]、[H+]为电池中各离子的瞬时浓度，单位为mol/L，[H+]=6 mol/L；z为电池反应转移电子数，z=1；Q 为气体常数；T为温度（K）；F为法拉第常数（96 500 C/mol）。一个电池单电堆由k个电池单体串联构成，其电动势Ust为：

本文以中科院大连化学物理研究所研制的100 kW全钒液流电池为基础进行模拟，其组成单元10 kW液流电池单电堆由40级电池单体串联构成，故每个电堆开路电动势表达式为：

考虑大容量液流电池由S个相应的电堆串联，则开路电压为：

2.4 LCFBS的SOC数学表达

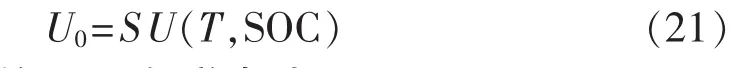
SOC反映液流电池储液罐中活性化学溶液的容量，随着电池的充电而增大，随着电池的放电而减小，其是一个不断变化的状态变量，其大小代表电池中的剩余能量。SOC的取值范围为0～1，SOC=0时表示电池完全放电，SOC=1时表示电池完全充满。电堆开路电压Ust用一个受控电压源表示，其大小受SOC变化和电池单体电压的影响，在电池充放电过程中连续变化。负载电流的大小与电池的荷电状态SOC、电堆电流Ist的大小有关。电堆的电流越大、SOC越小时，泵消耗的功率越大。SOC的计算公式如下：

其中，Est为电池充放电过程中可以使用的剩余容量；Ecap为电池充满时的总容量。

2.5 LCFBS的数学模型

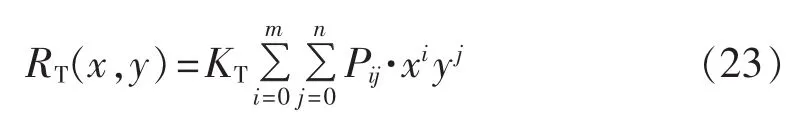
其中，KT为温度校正系数；Pij为多项式系数；x表征SOC；y表征串联级数。并联级数为1时，取m=3，n=LCFBS本身物理参数变化规律十分复杂，本文主要分析液流电池与电动势、SOC、内阻等有关的主要特性，暂不考虑其他次要特性如充放电时间等。

上文通过简化，利用动态内阻和动态电动势串联的模型来表征液流电池的主要特性。根据内阻公式（14）、（15），可以得到数学模型的内阻公式为：2；并联级数为2时，取m=4，n=2。需要注意的是，并非多项式最高次次数越高就会拟合精度越高，当最高次超过一定值时，拟合优度反而变差，即产生拟合边界数据振荡效应[17]。

根据式（23），可以得到内阻的矩阵表达形式为：

再根据式（21），可以得到液流电池开路电压：

输出直流电压即对应电池带载端电压Uout。Uout可由如下公式计算得到：

其中，Iload为实时负载直流电流。串并联级数可以在一定范围内任意给定，为便于下文仿真，利用离散计算方法实时计算SOC的大小，表示为：

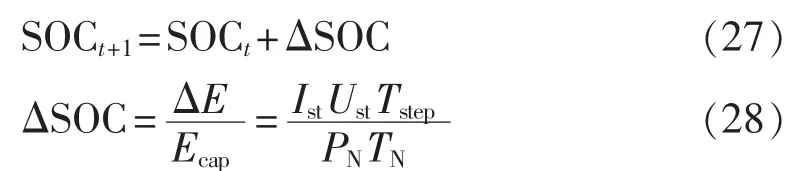
其中，Tstep为仿真步长，其值越小则仿真越精确；TN为额定时间，即为液流电池在额定功率PN下充满电所需的时间。ΔSOC与Ist的方向相同，充电时SOC呈不断上升的趋势；放电时SOC曲线则不断下降，其初始值则是用户自定义得到。

3 仿真验证

3.1 基本算法

图9 电池模拟器基本算法Fig.9 Basic algorithm of battery simulator

以电池的放电工况为例，充电工况下的情形与该工况类似。电池仿真程序中的主要物理量计算流程如图9所示，每次循环周期内控制程序的任务包括计算内阻、开路电动势、输出端电压，检测负载电流、计算负载功率等，进而对SOC进行实时更新计算并反馈影响下一周期的相应实时物理量，如此不断循环。

3.2 仿真模型及结果分析

仿真模型的搭建主要利用MATLAB中的Simulink模块，基于液流电池的数学模型搭建，其中内阻、电池开路电压、SOC等动态变化的参数利用f（u）函数构建。仿真结果数据见表7。

在 SOC=0.8，S=3，P=2，T=293 K，Ecap=80000J，负载2ω放电工况下，仿真波形如图10所示（仿真设置时间为40 s，SOC的下限为0.4）。

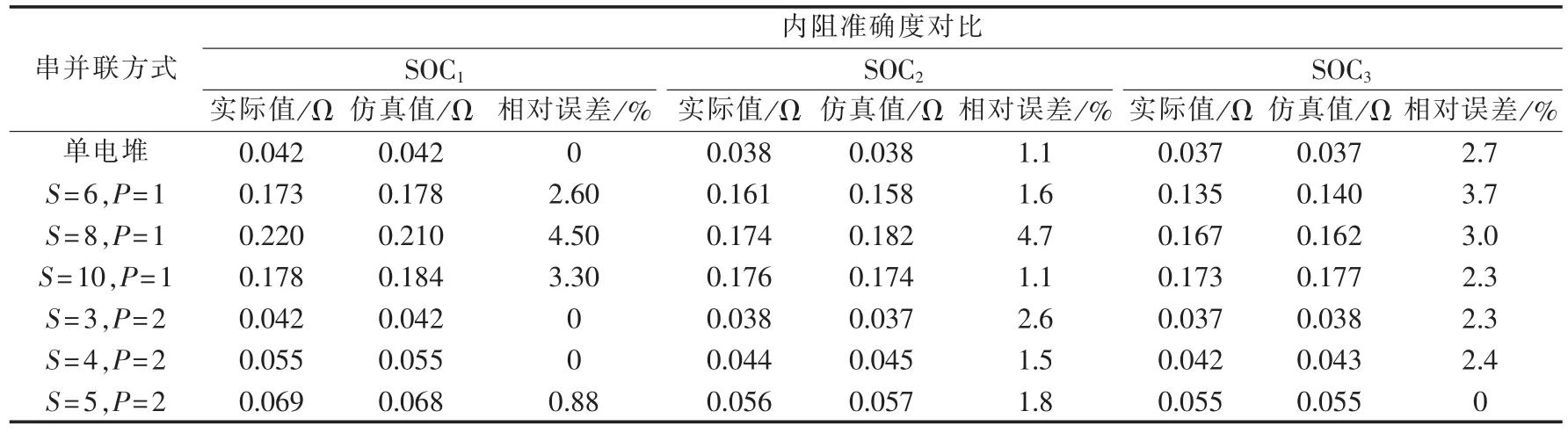
表7 内阻与S、P、SOC的关系Table 7 Relationship between internal resistance and SOCs for different configuration modes（S，P）

图10 仿真结果Fig.10 Simulative curves

电池处于放电工况，SOC从初始值线性减小，同时内阻变大，与实际数据的变化规律相同。内阻的仿真数据与原始数据的最大相对误差在5%以内，精度较高，支持用户自定义初始SOC、负载、串并联级数、温度等多种参数。

4 结论

本文基于100 kW液流电池系统的试验数据构建了数学模型，推导出便于核心参数计算的拟合公式。利用MATLAB/Simulink构建了其内阻、电动势和SOC的模型，仿真验证了该模型及其参数的精确性，可有效解决由液流电池电堆串并联构成的LCFBS的参数计算问题。

致 谢

本文以973课题《基于液流电池储能的多体系系统耦合及综合能量管理控制策略研究》系列报告之一《全钒氧化还原液流电池特性研究报告》相关研究中提供的大量液流电池的内阻数据为基础，在此表示感谢。