基于Nataf变换和准蒙特卡洛模拟的随机潮流方法
方斯顿,程浩忠,徐国栋,曾平良,姚良忠
(1.上海交通大学 电力传输与功率变换控制教育部重点实验室,上海 200240;2.中国电力科学研究院,北京 100192)
0 引言
近年来,电力市场化改革[1]和以风电为代表的可再生能源接入[2]给电力系统运行和规划带来更多不确定性,随机潮流PLF(Probabilistic Load Flow)计及这些不确定因素的影响,可综合分析系统的运行风险和薄弱节点,因而受到广泛关注[3-5]。
PLF 首先由 Borkowaska 于1974 年提出[6],40 年来,国内外学者对其进行了大量优化与改进,目前主要可分为解析法[7-10]和模拟法[11-13]两大类。解析法可分为卷积法[7]、半不变量[8-9]、点估计[10]。 卷积法利用输入变量分布函数的卷积运算得到输出变量的概率分布,计算量大。半不变量通过线性化潮流方程建立的线性关系将卷积运算转化为半不变量的代数运算,计算效率高但准确性差,得到的变量概率分布在首尾可能出现小于零的部分。点估计是已知输入变量的若干阶矩信息求取输出变量矩特征的数学方法,计算效率高,但高阶矩误差较大。
除卷积法外,解析法计算效率高,但误差均较大。而模拟法可准确地对实际物理过程建模,且建模质量不受变量分布性质、系统非线性的影响,因而比其他PLF方法更准确,其中蒙特卡洛模拟MCS(Monte Carlo Simulation)应用最为广泛。基于简单随机抽样SRS(Simple Random Sampling)的 MCS 收敛慢,获得准确解的计算代价大,因此,如何在保证精度的同时提高计算效率一直是MCS的研究热点。研究表明,样本的差异性[14]是影响MCS计算精度的主要因素。文献[11-13]采用各种基于拉丁超立方采样LHS(Latin Hypercube Sampling)的方法改进 MCS,但由于无法保证序列的低差异性,因此无法克服MCS收敛性的瓶颈。而以Sobol序列为代表的低差异序列LDSs(Low-Discrepancy Sequences)MCS 在计算精度和效率上均优于LHS,已在电子电路设计中取得了应用[14],但在随机潮流中的应用还没有见诸报道。
另一方面,为得到含相关性的样本序列,随机排序[15]、Cholesky 分解[16]、遗传算法[17]等改进排序方法均在MCS中得到应用。随机排序在样本较小时效果差;Cholesky分解仅针对相关系数矩阵正定的情况;遗传算法有迭代操作,结果较准确但计算耗时长。因此,本文提出采用奇异值分解的方法对样本进行排序,计算量与Cholesky分解相当,并可处理相关系数矩阵非正定的情况。
为提高MCS的计算效率并处理相关系数矩阵非正定的情况,本文提出一种基于Nataf变换和准蒙特卡洛模拟NQM(Nataf transformation based Quasi Monte Carlo simulation method)的PLF方法。首先利用Sobol方法产生服从均匀分布的LDSs,而后利用基于奇异值分解的Nataf变换生成服从输入变量联合分布的序列,再经过若干次确定型潮流计算得到输出变量的概率分布特性。对IEEE 30节点系统和我国某实际大区域电网的仿真验证了本文方法的有效性。
1 基于奇异值分解的Nataf变换
Nataf变换是在已知输入变量边缘分布的情况下重构联合分布的数学方法[18]。现将其过程简述如下:对任意 n 维输入变量 X= [X1,…,Xi,…,Xn]T,设其相关系数矩阵为[ρXij]n×n,其中 ρXij定义如式(1)所示。

其中,σi和 σj分别为 Xi、Xj的标准差;cov(Xi,Xj)为变量Xi、Xj的协方差;ρXij为相关系数。随机向量X可用Nataf变换转化为标准正态分布向量Z=[Z1,…,Zi,…,Zn]T:

其中,Fi为Xi的累积分布函数;Φ为标准正态分布的累积分布函数。设变换以后Z的相关系数矩阵为[ρZij]n×n,由 Nataf变换性质,[ρXij]n×n与[ρZij]n×n可根据式(3)相互转化:

其中,fXiXj(Xi,Xj)为 Xi、Xj的联合概率密度函数;μ、σ分别为相应变量的期望值与标准差;φZiZj(Zi,Zj,ρZij)为相关系数为ρZij的二维标准正态分布概率密度函数。本文采用文献[19]中方法对式(3)进行求解以求得[ρZij]n×n。 而由于[ρZij]n×n可能为非正定或非满秩阵,此时其Cholesky分解不存在,无法采用文献[16]的方法对样本进行排序。但一般相关系数矩阵都为对称阵,存在奇异值分解,本文通过证明定理1说明奇异值分解排序方法的过程。
定理1 设K为n维独立标准正态分布向量,矩阵UρZ∑1/2ρZ由向量Z的相关系数矩阵ρZ的奇异值分解生成:
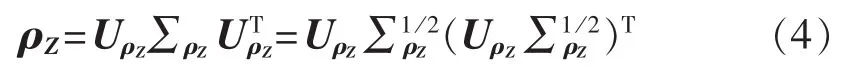
其中,UρZ为酉矩阵;∑ρZ为由矩阵奇异值构成的对角矩阵,并按从大到小排列。则由式(5)定义的Z*相关系数矩阵等于ρZ:

证明如下。
对∀z*i,其期望值满足式(6):
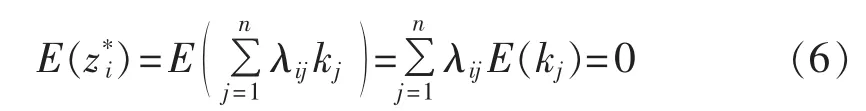
相关系数矩阵为:

因此,可根据定理1的步骤生成相关系数为ρZ的正态分布向量Z*,再通过Nataf反变换,可得到服从任意分布的随机向量X。
2 基于Sobol序列的准蒙特卡洛方法
2.1 MCS及其误差
在确定型潮流计算中,节点注入功率S与节点电压U、支路潮流B关系如式(8)所示。
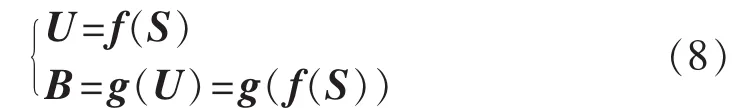
其中,S∈Ω为节点注入功率向量,Ω为节点注入功率空间;U为节点电压向量;B为支路潮流向量;f、g分别为由潮流方程导出的节点电压函数和支路潮流函数。而在PLF计算中,S、U和B均为随机变量,Ω为随机空间。在S的分布特性已知时,U和B的数字特征可由如式(9)所示的Stieltjes积分求取。

其中,EUk、EBk分别为 U 和 B 的 k阶矩;H(S)为 S的累积分布函数。这类积分当f、g形式复杂时很难求解,而MCS提供了求取这一积分的数值方法,求取方法如式(10)所示。

其中,Si为根据节点注入功率分布产生的序列;n为MCS次数。 为便于分析,将式(10)简化为式(11):

其中,Qn为n次模拟得到的数值结果;p代表式(9)中的被积函数,pi则代表式(10)中的 fk(Si)ΔH(Si)或 gk(f(Si))ΔH(Si)。 根据大数定律,MCS 估计得到的Qn会以概率1收敛到其真实值Q。

其中,P(·)为事件的概率。
积分的估计误差则可由定理2给出。
定理2[20]如果p的方差有限,即:

则MCS误差为:

由定理 2,当 p确定时,MCS以 O(n-1/2)的速度收敛于真实值。欲提高MCS的精度,则可以通过减小σ(p)或增大n来实现。以LHS为代表的方差缩减技术可以减小σ(p),因此相比于简单随机抽样,LHS可以提高MCS的精度,但从式(14)可以看出,其并不能改变收敛速度(仍然为O(n-1/2)),因而无法从本质上提高MCS的效率。下文将引入低差异序列改进MCS的样本生成方法,提高其收敛速度。
2.2 低差异性序列与准蒙特卡洛
基于低差异性序列的MCS称为准蒙特卡洛模拟 QMCS(Quasi Monte Carlo Simulation),目前已在电子电路设计中取得应用[14],精度和效率均优于基于拉丁超立方的方法。本文采用该方法进行PLF计算。首先,本文通过引入文献[20]的结论说明序列差异性与MCS精度的关系。
定理3[20]MCS误差可定义为:
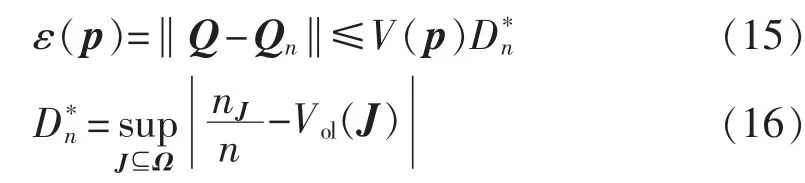

结合式(15),基于 LHS的 MCS收敛速度为O(n-1/2),与式(14)一致。 文献[23]指出,任意维度均匀分布序列最小Dn*如式(18)所示。满足该式的序列称为LDSs。

对比式(17)和(18),序列的 L∞-差异性由 O(n-1/2)变为 O(n-1),再结合式(15),引入低差异序列后 MCS的收敛速度可由 O(n-1/2)变为 O(n-1),从而大幅加快MCS的收敛。
2.3 NQM误差定义
为比较结合Nataf变换的SRS、LHS和NQM的误差,本文以SRS计算50000次的结果作为标准,定义估计误差为:
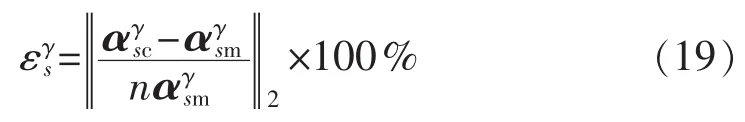
其中,εγs为相对误差指标;n为向量的维度;γ为输出变量类型,包括节点电压幅值、电压相角、支路有功潮流、支路无功潮流;s为数值特征,包括期望值μ与标准差 σ;αγsc为某采样规模下得到的输出结果;αγsm为SRS模拟50000次的结果。
因MCS收敛具有随机性,因此本文对在每一采样规模下均计算100次,将误差的平均值ε¯γs作为误差分析指标。
2.4 NQM计算流程
综合前文,NQM的计算流程如图1所示。简述如下:
a.输入基础数据,包括系统参数、节点注入功率的分布及其相关系数矩阵ρX、LDSs序列长度;
b.利用式(3)将ρX转化为标准正态向量的相关系数 ρZ;
c.利用文献[21]中方法生成0-1分布的独立LDSs序列矩阵Un×M,并利用标准正态分布的逆函数将其转化为正态分布的LDSs序列矩阵Dn×M;
d.利用步骤a中的方法将Dn×M转化为相关系数矩阵等于ρZ的正态分布序列矩阵
f.根据Xn×M进行M次确定型潮流计算,并统计得到各输出变量的数字特征及概率分布。
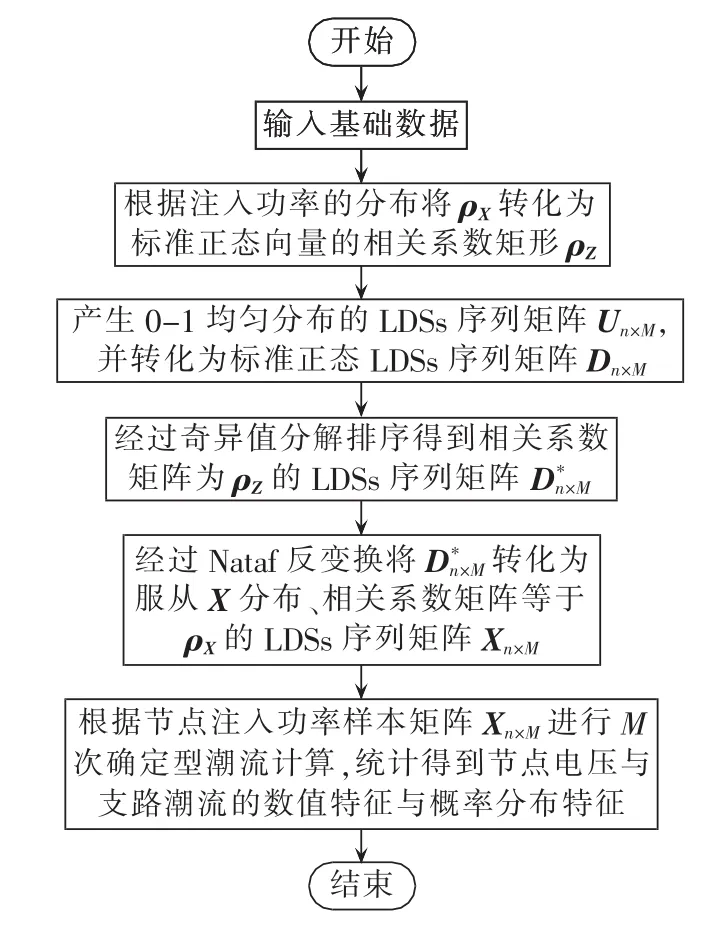
图1 计算流程图Fig.1 Flowchart of calculation
3 算例分析
3.1 算例介绍
本文所提算法分别采用IEEE 30节点系统和我国某大区域电网500 kV等值网络进行验证,该网络含节点1594个、发电机535台、线路3359条。2个算例分别采用SRS、LHS和NQM进行计算并分析误差。仿真平台基于MATLAB2013a,Intel Core dual i7-3820 3.6 GHz,RAM 8 GB。算例考虑的输入变量包括风电机组出力和负荷。假设风速满足威布尔分布 W(c,ξ)=W(10.7,3.97),风电场功率因数为 0.9,对于 IEEE 30节点系统,节点 3、4、6、28分别接入容量为15 MW的风电场;实际电网算例中的节点101—150均装设300 MW的风电场。
风电机出力的互相关系数均为0.9。负荷均为恒功率因数0.9,有功负荷服从期望为额定有功功率、标准差为期望5%的正态分布,互相关系数均为0.5。有功出力与风速关系满足:
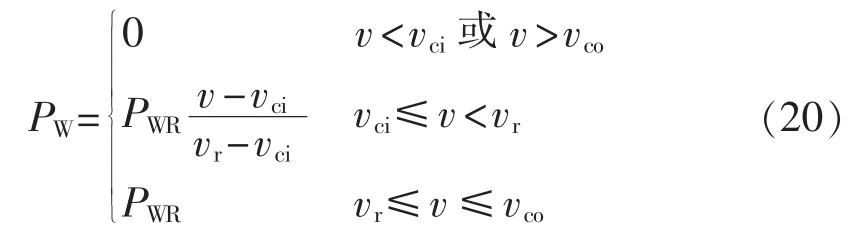
其中,PWR为风电场额定功率;vci、vr和 vco分别为切入风速、额定风速和切出风速,大小分别为2.5 m/s、13 m/s和 25 m/s。
3.2 NQM误差分析
分别利用SRS、LHS和NQM这3种方法对2个测试系统进行计算。按式(19)计算输出变量误差,分别表示为:节点电压幅值期望误差,标准差误差;节点电压相角期望误差,标准差误差;支路有功期望误差,标准差误差;支路无功潮流期望误差,标准差误差。 IEEE 30 节点系统输出结果见图2、3。实际网络计算结果见表1。
由图2、3及表1中数据可得:
a.当采样规模相近时,NQM和LHS的精度远高于SRS;
b.在输出变量的误差上,当系统规模较小时,NQM和LHS求得的期望值结果相近,但NQM收敛速度快于LHS,而在输出变量标准差的误差上,NQM精度远高于同样规模的LHS;
c.当系统规模扩大时,由NQM得到的变量期望值及标准差均优于LHS,且收敛更快。这说明NQM方法同样适用于实际大系统。

图2 IEEE 30节点系统电压幅值相角误差曲线Fig.2 Error curves of bus voltage magnitude and angle of IEEE 30-bus system

图3 IEEE 30节点系统支路潮流误差曲线Fig.3 Error curves of branch power flows of IEEE 30-bus system

表1 实际网络平均误差比较(N=1000)Table 1 Comparison of average errors of a practical power grid(N=1000)
用NQM还可以方便地得到输出变量的概率分布曲线。选取IEEE 30节点系统支路4-6有功潮流及实际网络中某线路无功潮流为研究对象,样本规模为50000的SRS作为标准结果,LHS计算800次和NQM计算500次的随机变量概率密度函数和累积分布函数比较分别如图4、5所示。
从图4、5中可得,无论系统大小,采样规模为500的NQM得到了与SRS计算50000次相近的结果,明显优于LHS计算800次的结果。这再次说明LDSs可克服蒙特卡洛收敛性的瓶颈,从而提高MCS的精度,节省PLF的计算时间。
3.3 NQM收敛趋势分析
为获得3种方法对特定变量的收敛趋势,本文以IEEE 30节点系统节点14的电压和支路6-8有功功率、实际网络某线路的无功功率为例;期望值与标准差随采样规模的变化趋势如图6所示,图中电压幅值均值、电压幅值标准差为标幺值。
图6中数据说明,3种方法的收敛趋势是相同的,但NQM收敛明显快于LHS和SRS,因此NQM可以在较短时间内获得较高的计算精度。

图4 IEEE 30节点系统支路4-6有功潮流概率分布曲线Fig.4 Active power probability distribution curves of branch 4-6 of IEEE 30-bus system

图5 实际系统某支路无功潮流概率分布曲线Fig.5 Reactive power probability distribution curves of a branch of a practical power grid
3.4 NQM计算时间分析
3种方法在不同采样规模下对IEEE 30节点系统和实际网络进行计算所花费的时间如表2所示。

图6 3种方法的结果比较Fig.6 Comparison of simulative results among three methods
从表2中数据可得,3种方法的计算时间相当,且均与采样规模成正比,证明计算时间大部分消耗在潮流计算上,而样本生成不会对计算时间产生大的影响。但由于LHS需要采样和排序的过程,相对计算时间略长。

表2 不同采样规模下3种方法计算时间Table 2 Computational time of three methods under different sample sizes
4 结论
以拉丁超立方为代表的伪随机采样无法保证序列的低差异性,这限制了MCS精度的提高。本文针对该问题,提出一种基于NQM的PLF方法。对IEEE 30节点系统和某实际电网的仿真证明了本文方法的有效性,并得到以下结论:
a.用LDSs序列可以克服MCS收敛性的瓶颈,因此NQM的收敛速度快于SRS和LHS;
b.使用奇异值分解对随机变量进行排序可在不增加计算量的情况下获得含相关性的随机序列;
c.SRS、LHS和NQM在期望值的计算结果上比较接近,而在标准差上NQM远远优于另外2种方法,在相同采样规模下可得到较精确的结果,因而生成的概率分布也较精确;
d.SRS、LHS和NQM 3种方法计算时间接近,而LHS由于采样方式的原因消耗时间略长于其余2种方法;
e.对我国某实际大区域电网的测试表明本文提出的算法对于大规模系统仍然适用。

