交直流互联系统对距离保护的影响分析及对策

费 彬，黄少锋，申洪明

（华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

高压直流输电（HVDC）在实现远距离、大容量、非同步电网互联等方面具有独特优势[1]。对受端交流系统而言，直流输电系统相当于一个快速动态电源，而其对交流侧故障十分敏感。交流侧发生故障引发的暂态过程中，由于换流站电力电子器件的非线性及直流控制保护系统的快速调节，直流系统的等值交流电流、阻抗、功率等电气量均会发生突变，从而造成此时的交流系统暂态特征与纯交流系统大不相同[2-9]，这必然会对现有交流继电保护的动作行为带来影响，严重时将引起交流保护的不正确动作。因此，深入研究交直流互联系统对交流电网继电保护的影响具有重要意义。

目前交直流混合输电系统的格局已在华东、华中、华南电网中形成，为了保障其安全稳定运行，国内华南理工大学、西安交通大学等科研单位对上述问题展开了研究并已取得卓有成效的成果。文献[7]分析了交直流互联系统中突变量选相元件的动作行为；文献[10]分析了直流系统等值电流作用于过渡电阻而造成测量电抗的变化，会造成距离保护的不正确动作；文献[11]对直流馈入运行环境下输电线路电流差动保护故障分量判据和稳态量判据的动作特性进行了分析；文献[12-14]通过建立直流系统等值工频变化量阻抗模型，分析了直流换相失败对工频变化量方向保护动作特性的影响。

在单端电气量的保护中，距离保护的优点相当突出，已成为高电压等级线路保护的典型配置之一。本文着重分析了距离保护在交直流环境下的运行特点：首先对传统交直流互联电网模型进行了分析改进，详细讨论了叠加原理在交直流互联系统中的适用性；并对交直流互联系统进行了故障分析，同时指出了交直流互联电网中零序电流的来源和分布特点。然后基于距离保护接线方式，研究了直流馈入对距离保护的影响，并提出了增加零序方向元件判别故障方向等解决措施。最后，利用PSCAD/EMTDC电磁暂态仿真程序验证了分析结论的正确性。

1 交直流互联系统的分析模型

1.1 传统交直流互联电网的分析模型

传统的交直流互联系统模型等效电路如图1所示，图1虚线框内包含了所要讨论的等值直流系统主要组成部分，包括逆变器、换流变压器、无功补偿装置及滤波器等。其中idc为逆变器交流侧等值电流；icap为流过交流滤波器及无功补偿装置的等效阻抗ZC的电流；idceq为整个等值直流系统注入交流系统的等值电流；ubus为交流母线电压。

图1 交直流互联系统等效图Fig.1 Equivalent diagram of AC-DC interconnected system

事实上，交流侧滤波器除了具有滤除谐波的作用以外，同时具备无功补偿的作用。但通过分析计算发现，对于工频量而言，滤波器组所呈现的阻抗主要为容性，电阻分量相对而言很小，可以忽略，因此可以将滤波器与电容器组等无功补偿装置结合在一起，仅以电容ZC来表示，如图1所示。

对于逆变器而言，外部交流母线电压的幅值及过零点变化会引起逆变侧直流电压的变化，从而造成直流电流发生变化。虽然在控制系统的作用下直流电流趋于保持恒定，但控制系统总是存在时延性，因此瞬时的直流电流增大不可避免。另外，在严重情况下交流侧故障引起交流母线的较大波动，将引发换相失败，此时直流电流的波动更大，且各个阀的导通情况也随之改变，此时注入交流系统的电流也会相应发生变化。从这个观点来看，将直流系统等值为一个压控电流源是合理的[9]，不妨记作 idc=f（ubus），见图1。由于直流系统包含了非线性的电力电子器件以及直流控制系统的快速调节，该受控源的表达式不易得到，目前主要由仿真获得。另外，现有的文献通常将idceq作为研究的重点，即无功补偿及滤波支路作为等值直流系统的一个组成部分，然后基于数字仿真获得idceq的暂态特性后分析对继电保护的影响。

1.2 改进的交直流互联系统模型

从时间尺度上，目前的继电保护原理均建立在傅氏算法的基础上，而傅氏算法是对单一数据窗内的采样数据进行分析处理。虽然整体而言，直流系统注入交流侧的电流是时变的，并且与交流母线电压ubus之间存在一个动态平衡的过程[6]，但对于某个给定的时间断面而言，该时间段内的注入电流是一定的，根据电路的替代定理，可将其用一个注入电流源代替。由于换流器的非线性以及直流控制系统的调节，此时的注入电流成分较为复杂，但总可以分解为基波、非周期分量以及各次谐波之和。仅就其中的工频量进行分析，则可以将其视为一个等值工频电流源。当数据窗移动到下一时刻时，上述分析仍然成立。

此外，由于换流变压器接线方式的原因，故障时其阀侧不会有零序电流流通，而无功补偿及滤波支路则可以为零序电流提供通路，基于上述原因，同时考虑到无功补偿及滤波支路的工频阻抗是确定可计算的，可将其作为交流系统的1条支路来进行分析，不再划归为等值直流系统的一部分，如图2所示。

图2 改进的交直流互联系统模型Fig.2 Improved model of AC-DC interconnected system

1.3 交直流互联系统的故障网络叠加

通过图2改进的分析模型可知，此时的模型显然满足叠加定理。在交流侧发生故障时，交直流互联系统相对于纯交流系统的故障特征主要表现在：对于纯交流系统而言，三相电源可视作恒定且对称的，而交直流互联系统中的直流等效电源在故障发生至恢复的暂态过程中是时变不对称的，从而表征出类似于故障点的特性，因此整个系统呈现出复故障的特征。本文将交流系统侧的短路点称为交流故障源，而故障后的直流系统称为直流故障源。对此可将直流电源分解为2个部分，即idc=idc0+Δidc，idc0为正常稳态时的注入电流，Δidc为直流故障扰动，如图3所示。如前所述，Δidc中势必包含了非周期分量以及谐波分量，但考虑到现有保护均是基于工频量，因此下文仅就工频量（以相量表示）进行分析推导。

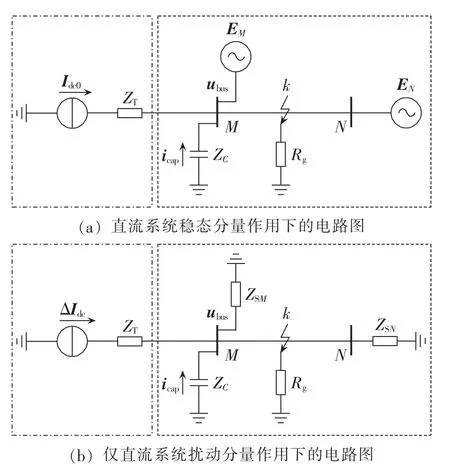
图3 叠加电路图Fig.3 Superposition circuit diagrams

图3（a）在故障前后两侧电源都是恒定且三相对称的，仅存在交流侧故障源，与传统纯交流系统类似，因而仍然可以采用序分量法进行分析。对于图3（b），仅存在直流故障源，由于此时三相电路的参数并不对称（包括电源以及故障点的参数），因此，序分量法不再适用。

2 换相失败对距离保护的影响

2.1 故障分析

直流馈入对距离保护的影响主要在于直流系统等值工频电流作用于过渡电阻而造成的测量阻抗变化[10]，考虑到相间距离继电器几乎不受过渡电阻的影响，因此本文主要分析接地阻抗距离继电器。下面以单相接地故障为例，分析直流馈入环境下的各个保护测量电气量。对图3（a）分析时，相当于仅考虑了交流故障源，此时的各序网络如图4所示。

注意到换流变压器的网侧为Y型接地接法，而阀侧为△型或Y型接法，因此零序网络中包含了换流变压器的零序阻抗，如图4（c）所示。

利用序分量法计算，可得故障点的各序电流为：

图4 序网图Fig.4 Sequence-network diagrams

显然，故障点电流Ikac=3Ik0。

保护安装处的各序电流为：

其中，ZLM1、ZLM0分别为短路点k到M侧的正序、零序阻抗；ZLN1、ZLN0分别为短路点k到N侧的正序、零序阻抗；ZSM1、ZSM0分别为M侧交流系统的正序、零序阻抗；ZSN1、ZSN0分别为N侧交流系统的正序、零序阻抗；CM1、CM0分别为M侧的正序、零序电流分配系数；ZC为交流滤波器及无功补偿装置的等效阻抗。

由此可得保护安装处的测量电流为：

对于图3（b），只考虑了直流系统故障源，由于三相系统参数不对称，因此需要在abc坐标中计算，为了计算简便，仅考虑故障相，可得保护安装处及故障点的电流为：

其中，ΔIdc为直流系统引起的故障扰动分量；CMDC为仅在直流故障源作用下M侧的电流分配系数；CkDC为故障支路的电流分配系数；IMDC为此时M侧的测量电流；IkDC为此时流过故障支路的电流。

值得指出的是，对于工程中常用的双桥12脉动逆变器，由于其换流变压器的网侧为Y型接地，阀侧为Y型不接地或者△型，因此无论交流系统是否发生接地故障，直流系统的等效故障源均不会向交流系统注入零序电量，因此式（2）中的零序电流即为保护安装处所流过的全部零序分量。

综上所述，对应于接地阻抗距离继电器的接线方式，可得：

其中，c 为本线路的零序补偿系数，c=（Z0-Z1）/Z1，Z0、Z1分别为线路单位长度的零序及正序阻抗。

而短路点的故障电流为：

2.2 直流馈入对距离保护的影响

直流馈入对距离保护的影响主要体现在直流系统等值电流作用于过渡电阻时所引起的测量阻抗附加项[10，15]：

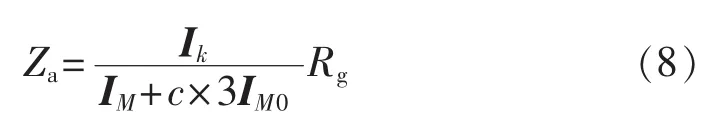
由2.1节的分析得到了相应的Ik、IM及IM0的表达式，因此可以分析Za在不同系统运行条件下的性质：

为了分析方便，记 X=Ik0、Y=ΔIdc，以 Ik0为相位基准，讨论上式中（AX+BY）/（CX+DY）的情况。

分析中将 A、C 近似视为常数，B／D=（ZLN+ZSN）÷（ZLN+ZSN+Rg），因而BY的幅值比 DY小，且相位超前于DY一定角度。由于Ik0与ΔIdc的相位关系不确定，因此对其需进行全面的讨论，但总体可以分为下面3种情形（以Ik0作为坐标平面的横轴）。

a.BY、DY同位于坐标平面的上半平面。

由图5可知，AX+BY与CX+DY之间的相位关系取决于A与C的相对大小。当A＞C时，AX+BY滞后于CX+DY，即此时的测量阻抗附加项Za呈阻容性；当A＜C时，AX+BY的相位随着C的增加而逐渐由滞后转为超前，当C＞C′时，AX+BY将超前于CX+DY，所以Za逐渐由阻容性转变为阻感性。

图5 情形1下电气量之间的相位关系Fig.5 Phasor relation among electrical variables in case 1

b.BY、DY同位于坐标平面的下半平面。

由图6可知，AX+BY与CX+DY之间的相位关系仍取决于A与C的相对大小。当A＞C时，AX+BY超前于CX+DY，即此时的测量阻抗附加项Za呈阻感性；当A＜C时，AX+BY的相位随着C的增加而逐渐由超前转为滞后，当C＞C′时，AX+BY将滞后于CX+DY，即Za逐渐由阻感性转变为阻容性。

图6 情形2下电气量之间的相位关系Fig.6 Phasor relation among electrical variables in case 2

c.BY、DY分别位于坐标平面的上、下半平面。

由图7可知，AX+BY与CX+DY之间的相位关系不再取决于A与C的相对大小，而仅由BY和DY的相位决定。当BY位于上半平面而DY位于下半平面时，AX+BY超前于CX+DY，Za呈阻感性；反之则 AX+BY滞后于 CX+DY，Za呈阻容性，如图7（b）所示。

图7 情形3下电气量之间的相位关系Fig.7 Phasor relation among electrical variables in case 3

值得指出的是，由于直流自身控制保护系统的快速调节，直流扰动量ΔIdc处于不断变化之中，因此ΔIdc与Ik0之间的相角差随着数据窗移动是不断变化的，会导致BY、DY的相位关系出现不同的情形。而对于不同故障位置、不同严重程度的故障，它们之间的相位关系也不一样，导致测量阻抗附加项可能呈阻感性或阻容性，这就与纯交流系统中阻抗附加项主要取决于两侧系统功角而呈现单一的性质有所不同。对于N侧的分析与此类似，限于篇幅，不再赘述。

2.3 影响分析及对策

综上分析可知，交直流互联系统的测量阻抗可能呈现感性，也可能呈现容性。对于保护而言，需要考虑极端情况。

情况1：保护出口故障时Za呈现容性，使得实际的测量电抗很小甚至小于0，表征出反方向的故障特征，进而造成保护拒动。

情况2：对于保护范围末端故障，由于Za呈现感性，使得实际测量电抗大于整定值，超出Ⅰ段保护范围而由本侧Ⅱ段动作，造成保护动作延时。

值得指出的是，对于情况2，当保护范围末端故障时是可以允许延时动作的，所以对保护的影响并不大。

为了提高距离保护的动作性能，通常采用能容许较大过渡电阻而不至于拒动的测量元件动作特性作为主要措施[16]，如采用四边形特性等，但在某些极端工况下仍具有其局限性。对于上述情况1，显然希望M侧保护的阻抗元件能够区分故障方向，防止保护拒动。由2.1节分析可知，对受端交流系统而言，零序电流的分布与直流系统无关，即零序网络不包含背后直流系统而与纯交流系统类似。因此，在保护安装处背后系统阻抗呈感性的情况下，可采用零序方向元件来区分故障方向，同时在正方向故障时不会对保护带来影响，具体判别过程如图8所示。图中，Xm为保护安装处的测量电抗；Xset为整定电抗；Um0、Im0分别为保护安装处测得的零序电压、零序电流。

图8 防拒动措施Fig.8 Measure against refuse-to-act

3 仿真验证

3.1 模型说明

本文所用仿真模型如图9所示，图中直流系统采用国际大电网会议CIGRE的HVDC标准模型，受端交流系统为双电源系统，M侧、N侧系统短路容量分别为 SM=4.0 p.u.、SN=2.5 p.u.。线路 MN全长为100 km，参数为：r1=2.5×10-5Ω/m，x1=3×10-4Ω/m；r0=7.5×10-5Ω/m，x0=9×10-4Ω/m。 交流滤波器及无功补偿装置的等效工频阻抗ZC=1.9-j84.4ω，换流变压器的零序阻抗ZT0=j16ω。采样频率为4000 Hz，所有故障均设置在0.5 s发生，持续时间为0.1 s。

图9 PSCAD仿真模型Fig.9 PSCAD-based simulation model

3.2 仿真分析

3.2.1 远端故障时的仿真结果

图10是在线路距M侧60 km处发生A相经30ω过渡电阻接地（记为故障1）时的仿真结果。其中图10（a）为以Ik0为相位基准时的ΔIdc的相位，图10（b）为对应的测量阻抗附加项中的电抗部分，可以看到其随着数据窗的移动时刻变化。为方便分析，表1中给出了根据上述网络参数计算得到的对应于式（9）中的系数 B、D。 由图10（a）可知，ΔIdc滞后 Ik090°以上，因而此时的BY、DY应都位于坐标轴的下半平面。由2.2节的分析可知，测量阻抗的附加项呈感性，如图10（b）所示。这将造成测量阻抗偏大，当故障处于距离保护Ⅰ段范围末端时可能超出保护范围而由Ⅱ段动作，造成保护的延时动作。

图10 距M侧60 km处故障的仿真结果Fig.10 Simulative results for fault at 60 km from M-side

表1 不同故障情形下的比例系数Table 1 Coefficients for different faults

3.2.2 零序电流的特性分析

图11为该故障情形下换流变压器两侧的零序电流标幺值分布。图11（a）为Y/Y0换流变压器两侧的零序电流分布，图11（b）为△/Y0换流变压器两侧的零序电流分布。由图11可以看出，无论是何种接线的变压器，其阀侧零序电流几乎为0，因此零序网络不包括背后的直流系统，即直流馈入不会改变网络中零序电流的分布。 此外，对比图11（a）、（b）可知，Y/Y0换流变的网侧零序电流相对于△/Y0换流变小很多，这是由于前者的零序阻抗主要取决于励磁支路，因而其零序阻抗远大于△/Y0换流变，所以分流较小。

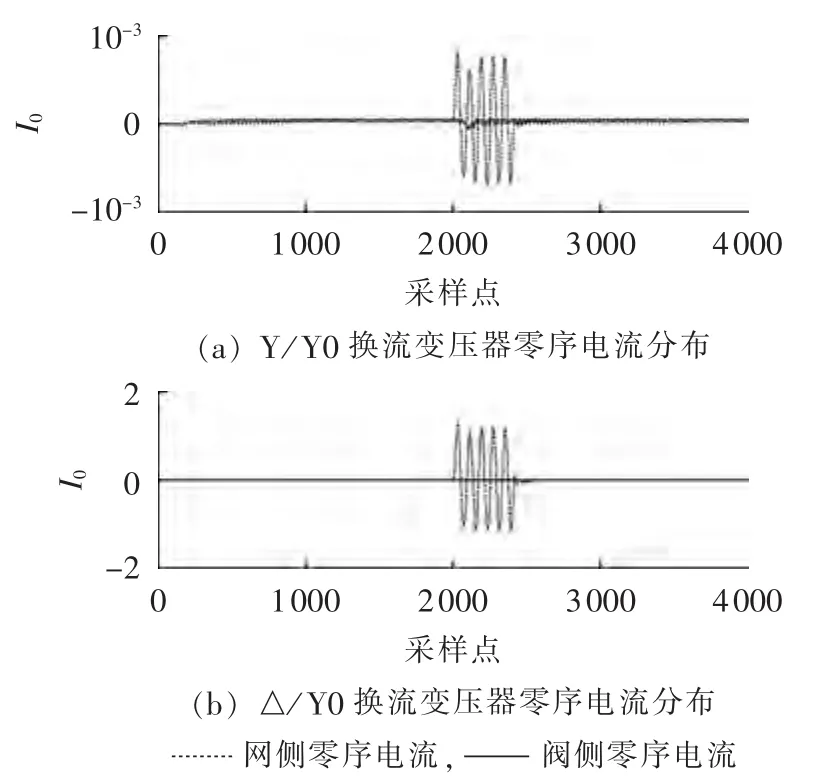
图11 零序电流分布图Fig.11 Distribution of zero-sequence current

为了进一步地验证直流扰动不会影响网络中零序电流的分布和大小，图12中考虑了纯交流系统中发生故障的情况，图中电流为标幺值。对于无直流系统的情况，通过改变两侧交流系统的功角使线路上传输的功率与含直流系统时相当。由图12可知，在2种情况下发生相同故障，保护安装处的零序电流变化几乎相同，从另一个侧面说明了，交流侧故障是零序电流的主要来源。

图12 直流馈入对零序电流的影响Fig.12 Impact of DC feed-in on zero-sequence current

3.2.3 近端故障时的仿真结果

图13是在线路距离M侧5 km处发生A相经75ω过渡电阻接地（记为故障2）时的仿真结果。此时的系数B、D如表1所示。结合图13（a）分析可知，BY、DY都将位于坐标轴的上半平面，因而测量阻抗附加项Za应呈容性，如图13（b）所示。对于M端距离保护而言，Za呈容性将使得保护安装处感受到的电抗值减小，对于欠量动作的距离保护而言有利于其正确动作；但对于保护出口附近的故障，有可能使得保护感受到的阻抗也为容性，即类似于反方向故障的特征，引起保护的拒动。

图13 距M侧5 km处故障的仿真结果Fig.13 Simulative results for fault at 5 km from M-side

3.3 防范措施的仿真

图14表示的是零序方向元件的判别结果，其中图14（a）为正方向 k 处故障，图14（b）为反方向 k′处故障，其他故障条件与图13相同。由图14可知，零序方向元件能够准确判断故障方向，结合阻抗元件的判别结果即可保证距离保护不发生拒动。

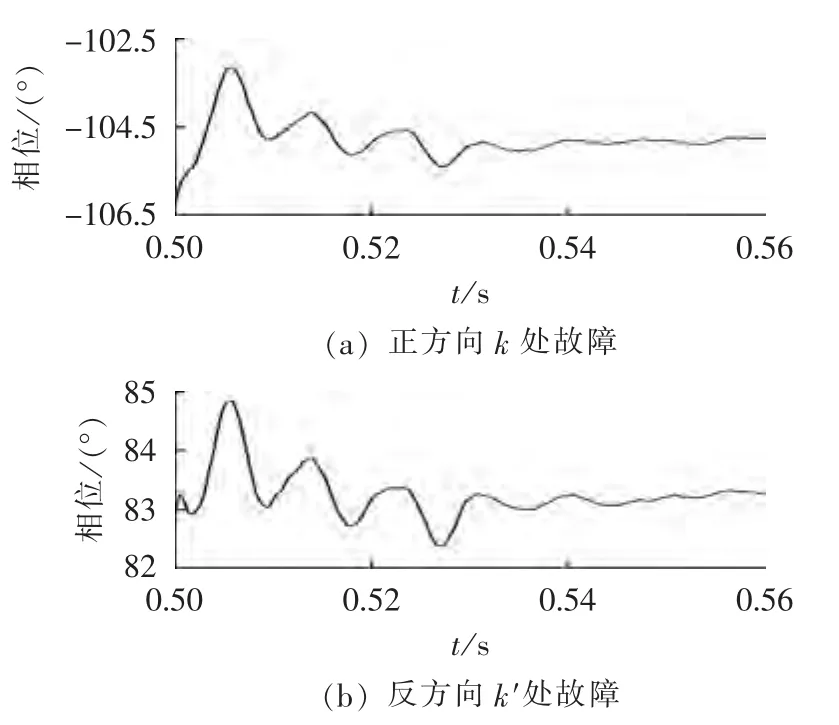
图14 零序方向元件仿真结果Fig.14 Simulative results of zero-sequence directional element

综上分析可知，交流侧发生故障时，由于直流系统注入交流侧的电流发生剧烈的变化，使得保护安装处的测量阻抗在故障发生至恢复的暂态过程中不能得到准确的测量，可能会导致保护不正确动作或延时动作。此外，对于M侧保护而言，测量阻抗附加项呈现阻容性或阻感性与很多因素有关，相较于纯交流系统仅取决于保护安装在送点侧或受电侧并呈现单一的性质有所不同。

4 结论

a.对传统交直流互联系统模型进行了详细的分析和改进，使改进后的模型适用于叠加定理。

b.交流系统故障是引起零序电流的主要原因，直流等值系统并不会向交流侧注入零序电流，也不会影响到零序电流的分布。

c.测量阻抗附加项随着直流等值故障电流的变化而变化，即随着数据窗的移动而时刻变化。不同严重程度的故障情况引起的附加阻抗性质不同，可能呈感性或容性，由此可能引起保护的拒动或延时动作。针对保护出口附近故障可能引起的拒动，提出的增加零序功率方向判别的措施可以有效解决这个问题。