基于改进K-means聚类算法的供电块划分方法

韩 俊，谈 健 ，黄 河，乔黎伟

（1.国网江苏省电力公司经济技术研究院 规划评审中心，江苏 南京 210008；2.国网江苏省电力公司 发展策划部，江苏 南京 210008）

0 引言

对于供电范围较大的供电区域，110 kV（35 kV）变电站数量庞大、布点散乱，如果直接进行该区域的网架结构优化研究工作，那么其工作量将会非常大，方向性比较难把握，任务艰巨，且不一定收到很好的成效。

传统规划常以行政区域为边界来划分供电区域，没有考虑电网的实际情况。本文将影响供电区域划分的多种因素考虑在内，将各种因素的影响量化，探索数学约束条件，以求寻找一种综合考虑电网实际情况的供电区块划分方法。

为了进一步提高配电网优化规划［1-12］的效率及精细化程度，避免对不存在联络关系的变电站进行无谓的搜索计算，本文以聚类分析思想为基础，提出了基于改进K-means聚类算法的供电块划分方法，将大范围的供电区域合理地切割成若干小规模的供电块，分别针对各个供电块开展网络结构的优化规划研究，这样层次清晰、工作重点明确，且规划效果明显。

1 基于改进的K-means聚类分析算法

1.1 聚类分析的概念

所谓聚类就是按照事物的某些属性，把事物聚集成类，使类间的相似性尽可能小，类内相似性尽可能大。聚类是一个无监督的学习过程，它同分类的根本区别在于：分类是需要事先知道所依据的数据特征，而聚类是要找到这个数据特征。因此，在很多应用中，聚类分析作为一种数据预处理过程，是进一步分析和处理数据的基础［13］。

一个能产生高质量聚类的算法必须满足下面2个条件［14］：类内数据或对象的相似性最强；类间数据或对象的相似性最弱。

1.2 K-means聚类算法的基本原理

K-means聚类算法是一种硬聚类算法，是典型的基于原型的目标函数聚类方法的代表，它以数据点到原型（类别中心）的某种距离之和作为优化的目标函数，利用函数求极值的方法来得到迭代运算的调整规则［15-16］。

1.3 K-means聚类算法的优点和不足

a.与层次聚类相比，K-means聚类算法可以得到更紧密的簇，尤其是对球状簇；

b.对大数据集，K-means聚类算法是可伸缩和高效率的；

c.K-means聚类算法尝试找出使平方误差函数值最小的k个划分，当结果簇是密集的，而且簇和簇之间区别明显时，效果较好；

d.K-means聚类算法需要用户预先指定聚类的个数，但在大多数实际应用中，最终的聚类个数是未知的，这在一定程度上限制了该聚类算法的应用；

e.对于k个初始中心点的选取是随机完成的，而初始中心点选取的不同会导致不同的聚类结果，这种随机选取初始聚类中心的方法将会引起聚类结果的不稳定性。

1.4 K-means聚类算法的改进策略

本文针对传统K-means聚类算法的不足，从初始中心点的选取和划分数k的确定这两方面提出相应的改进措施。

1.4.1 选取初始中心点的方法

本文针对K-means聚类算法的不足，提出了改进的初始中心点的选取方法，通过样本间平均距离［17］的引入，能够很好地体现数据的分布情况，使得初始中心点尽可能地趋向于比较密集的范围内，从而进行更好的聚类。

假设待聚类对象 X=｛xi|xiєRP，i=1，2，…，n｝，k个聚类中心用 Z1、Z2、…、Zk表示，有如下定义。

定义 1 2 个 P 维向量 xi=（xi1，xi2，…，xiP）T和 xj=（xj1，xj2，…，xjP）T间的距离用欧氏距离表示：

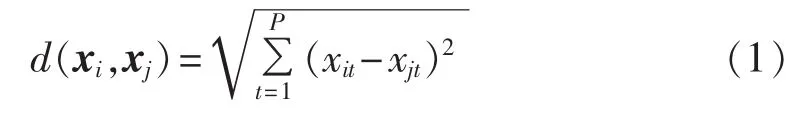
定义2 样本点间的平均距离dmean为：

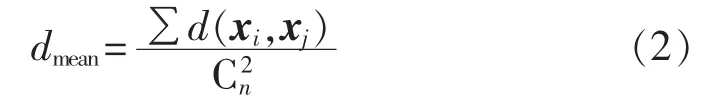
1.4.2 最佳聚类划分数k的选取方法

K-means聚类算法在供电块划分方面的应用是以确定的供电块划分数k为前提对变电站进行分块划分的。在实际操作中，k值是难以准确界定的，本次研究以类间类内划分BWP（Between-Within Proportion）指标［18］来确定供电块划分的最佳分块数。BWP指标是一种基于样本几何结构，以数据集中某个样本为研究对象，对聚类结果进行有效性分析的指标，主要计算公式如下：

其中，ni为第 i个供电分块中的变电站数；aBWP（k）为供电块划分为k个时BWP指标的平均值；argmax［］为一函数，其返回aBWP（k）取最大值时的k值。

该指标反映了单个样本的聚类有效性情况，指标值越大，说明单个样本的聚类效果越好。通过计算数据集中所有样本的BWP指标的平均值来分析该数据集的聚类效果，平均值越大，说明该数据集的聚类效果越好。

2 基于改进K-means聚类算法的供电块划分方法

2.1 供电块划分与点的聚类划分间差异性分析

2.1.1 变电站圆形等效供电半径的折算

为了综合考虑变电站配置和负荷密度等多种因素，在供电块划分过程中就必须考虑变电站的供电范围，供电块划分问题也因此由平面点划分的问题转化为面积域划分的问题。本次研究为了便于供电块的划分，把变电站的供电范围近似等效为圆。

a.供电范围内负荷密度均匀的情况。

当变电站圆形等效供电范围内负荷密度均匀时，可按照目前计算变电站圆形供电半径的方法。从规划区域的角度出发，根据变电站圆形供电范围内负荷密度的大小和供电圆的面积，折算出的等效供电半径可按下式计算：

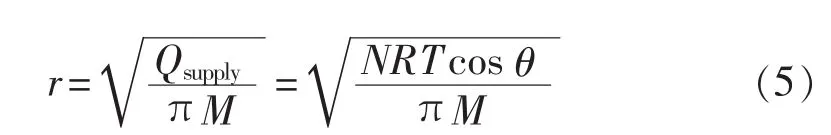
其中，R为变电站单台主变容量；N为主变台数；T为满足主变N-1条件下的最大负载率；cosθ为功率因数；M为变电站圆形供电范围内的负荷密度；r为变电站圆形供电范围的半径。

b.供电范围内负荷密度不均匀的情况。

变电站圆形等效供电范围包含不同负荷密度区域时的示意图如图1所示。

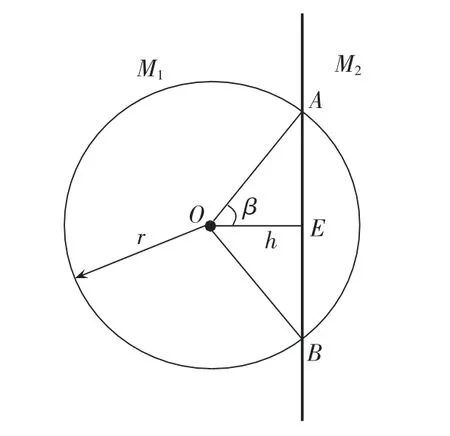
图1 基于不同负荷密度的变电站等效供电范围Fig.1 Equivalent power-supplying range of substation based on different load densities

以负荷等价为纽带，经分析有下式成立：

其中，S1、S2分别为负荷密度 M1、M2下部分等效供电圆的面积。经过数学分析，式（6）不一定存在满足要求的解，故在求解变电站圆形等效供电范围的半径时不能按照上式获得精确解。

在变电站圆形等效供电范围内各种负荷密度的分块所占面积求解的基础上，得出变电站等效圆形供电范围半径近似解的表达式如下：

其中，m为变电站等效圆形供电范围内包含负荷密度的类数；Si（r′）为第i类负荷密度的分块在变电站等效圆形供电范围内的面积，其为r′的函数；δ为灵敏度系数，表示误差的范围。

2.1.2 变电站界间距概念的定义及计算

a.问题的提出。

供电块划分的目的是为了便于各供电块内变电站之间联络结构的优化规划，而变电站之间是否互联与变电站之间的地理距离和变电站各自的供电范围都有紧密的联系。同时，变电站圆形等效供电范围的确定就为变电站间互联与否的判断提供了参考依据。

从图2可以看出，左图中变电站sub1和变电站sub2间的地理距离d1，2小于右图中变电站sub3和变电站sub4间的距离d3，4。假设变电站的供电范围为圆形，在左图中，由于变电站附近负荷密度过大，供电半径很小，这2座变电站的供电范围没有交集，因此2座站互联的可能性较小；相反在右图中，由于变电站附近负荷密度很小，供电半径较大，2座变电站的供电范围出现了重合的部分，因而变电站之间建立联络的可能性较大。因此本文在进行供电块划分时，不能简单地考虑变电站间的欧氏（地理）距离，故在此基础上引入了变电站界间距的概念。

图2 不同地理距离下2座变电站间的联络示意图Fig.2 Schematic diagram of connection between substations for different geographic distances

b.变电站界间距的概念及计算方法。

变电站界间距是指在假定2座变电站供电范围为圆形的前提下，其圆形供电范围的近侧圆弧之间相离程度的大小。设平面上2座变电站的编号为i、j，其坐标分别为（xi0，yi0）和（xj0，yj0），等效圆形供电半径分别为ri和rj，则两者之间的欧氏（地理）距离d（i，j）和界间距 D（i，j）间的关系如下所示：

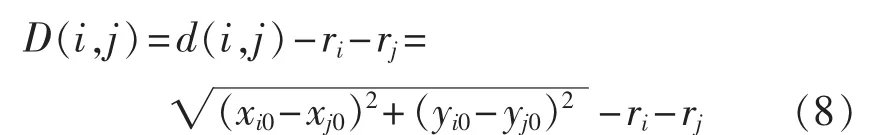
由上式可知，D（i，j）的取值有 3 种类型：D（i，j）>0；D（i，j）=0；D（i，j）<0。 不同取值情况下的变电站界间距示意图如图3所示。

D（i，j）>0表示2座变电站的圆形供电范围没有交集，说明2座变电站不存在共同带负荷的情况，D（i，j）越大，2座变电站建立联络的可能性越小；D（i，j）≤0表示2座变电站的圆形供电范围有交集，说明2座变电站可能存在共同带负荷的情况，D（i，j）越小，变电站间建立联络的可能性越大。

2.2 改进K-means聚类算法在供电分块中的应用

2.2.1 供电块初始聚类中心的形成

在已知供电块划分块数k的基础上，首先生成一组供电分块初始聚类中心的位置集合。每座变电站都可以用二维平面上的一个点表示，每一个点存在（x，y）坐标。结合变电站的实际地理位置，以变电站界间距的计算结果为依据，筛选出最可能存在于同一分块内的变电站，以其界间距的中心点作为分块聚类中心的初始位置，迭代过程中利用每次迭代各供电分块中变电站的不同，在初始位置的基础上搜索，找到最终合理的位置值。供电分块初始聚类中心形成的具体步骤如下。

图3 不同取值情况下的变电站界间距示意图Fig.3 Schematic diagram of distances between substation boundaries for different values

a.将供电区域内的变电站编号为1、2、…、n，按式（8）计算任意 2 座变电站间的界间距，记为 D（i，j），并计算所有界间距的平均值，如下所示：

b.对所有界间距按照由小到大的顺序进行排序，存入向量D中，将最小的界间距对应的中心点作为第一个初始聚类中心，其坐标z1计算方法如式（10）所示：

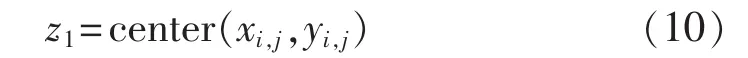
其中，center（xi，j，yi，j）为变电站 i和变电站 j的界间距的中心点坐标。

c.计算出变电站次小界间距所对应的中心点坐标，同时算出它与先前已确定的初始聚类中心的距离并与界间距的平均值lmean进行比较，若它与先前已有初始聚类中心的距离均大于等于lmean，则将该界间距对应的中心点作为下一个初始聚类中心；否则，重复步骤c。

d.当初始聚类中心的个数没有达到k，而所有界间距却又全部经过判断时，则动态缩小界间距的平均值，并清空步骤c中寻找到的初始聚类中心，重复步骤c。

e.当初始聚类中心的个数达到k时，则认为初始聚类中心完全形成，待迭代结束后求得最终的聚类结果。

2.2.2 最佳供电块划分数k的确定

设K=｛X，R｝为供电块划分的聚类空间，其中X=｛x1，x2，…，xn｝为变电站样本集合，假设 n 座变电站样本被划分为k个分块，则有相似定义如下。

定义1 定义第i个供电分块中的第j座变电站的最小块间界间距b（i，j）为该变电站到其他每个供电分块中变电站平均界间距的最小值，根据供电块划分的实际情况，应该有 b（i，j）>0 成立，如下式所示：

其中，c表示供电块被分为c类；nl为第l类供电块中变电站数为第l类的第p个样本为第i类的第j个样本。

定义2 定义第i个供电分块中的第j座变电站的块内界间距w（i，j）为该变电站到第i个分块中其他所有变电站界间距折算值的平均值，如下式所示：

特别指出的是，根据变电站界间距的定义和计算方法，供电块内的变电站界间距计算值有正有负。为了提高供电块划分的有效性，在计算块内界间距w（i，j）时需要把变电站界间距折算成非负值。

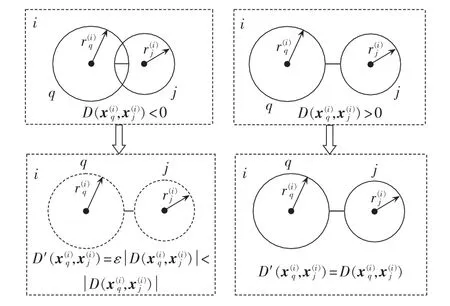
图4 变电站界间距折算示意图Fig.4 Schematic diagram of distance conversion between substation boundaries

如图4所示，左图中变电站间界间距小于0，右图中变电站间界间距大于0，且两者绝对值相等。显然，左图中2座变电站的块内紧密性要强于右图，因此左图中变电站间界间距的折算值应要小于右图中变电站间的界间距，因此，引入折算因子ε。

定义3 定义第i个供电分块中的第j座变电站的聚类界间距abw（i，j）为该变电站最小块间界间距 b（i，j）与块内界间距 w（i，j）之和。

定义4 定义第i个供电分块中的第j座变电站的聚类离差界间距sbw（i，j）为该变电站最小块界间距 b（i，j）与块内界间距 w（i，j）之差。

定义5 定义第i个供电分块中的第j座变电站的类间类内划分指标BWP（i，j）为该变电站的聚类离差界间距和聚类界间距的比值，如下式所示：

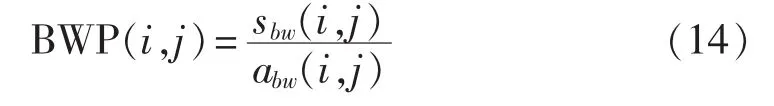
BWP指标是从变电站界间距测度考虑，就是使供电分块内变电站间界间距极小化而供电分块间界间距最大化的划分是最优划分。但是这样可能会导致选取的划分方案中某些供电分块内变电站数量过多，而某些供电分块内出现孤立变电站的情况。因此，为了解决这一问题，本文定义了供电块划分均衡性指标，对aBWP（k）值较大的几种划分方案计算其均衡性水平，然后综合考虑2种指标水平确定供电块最佳划分数k。供电块均衡性指标β（k）的计算方法如式（15）所示：

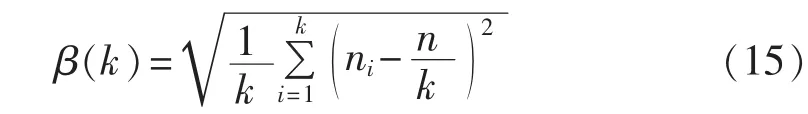
需要指出的是，该指标为负型指标，即指标取值越小，供电块的均衡性水平越高，在此基础上确定供电块划分的最佳分块数。

2.2.3 供电块划分的整体流程

基于改进K-means聚类算法的供电块划分详细流程如图5所示，图中η为界间距平均值lmean的动态调整系数。

需要特别指出的是，当聚类集合中只有1座变电站时，其聚类中心在迭代过程中保持不变。

3 实际算例分析

某地区远景期规划建设110kV（35kV）变电站28座，其中变电站布点规划结果及负荷密度分布情况如图6所示。

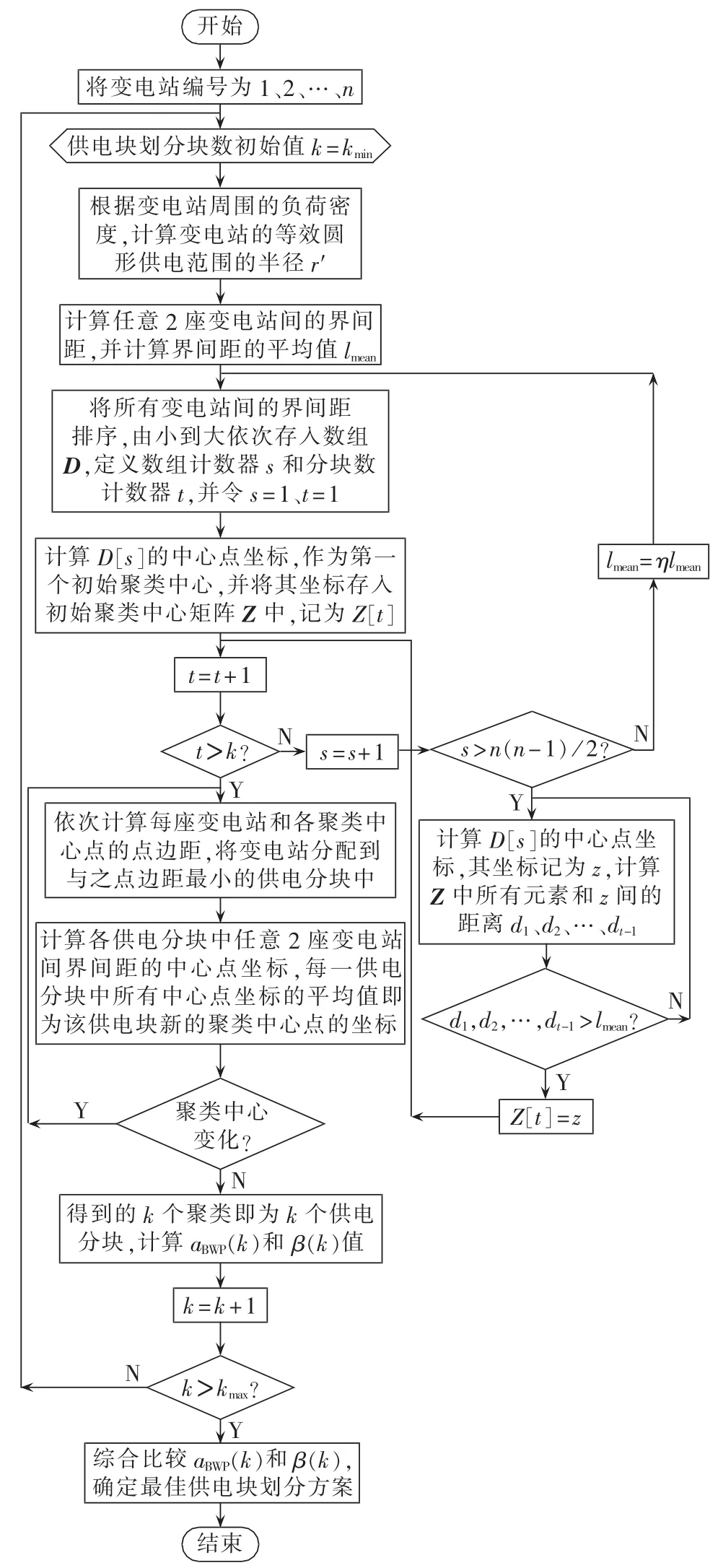
图5 基于改进K-means聚类算法的供电块划分流程Fig.5 Flowchart of power-supplying block partition based on improved K-means clustering algorithm

选取该地区左下角为原点建立坐标轴，则可以得到所有变电站的相对位置坐标，以远景期规划变电站的配置规模和区块负荷密度为基础数据，折算每座变电站的圆形等效供电半径。然后根据本文提出的基于改进的K-means聚类算法进行供电块的划分，供电块划分数k的取值范围为2～10，不同划分方案情况下平均BWP指标和均衡性指标β的计算结果如表1所示。

结合表1中不同供电块划分方案下的平均BWP值和供电块划分均衡性水平指标β的对比分析，划分数为9时的平均BWP值远远高于其他划分方案，因此，该供电区域划分方案选取划分数为9时的方案为最佳供电块划分方案，供电块最终划分方案如图7所示。

图6 某地区远景期变电站规划布点及负荷密度分布图Fig.6 Planned substation allocation and load density distribution for a region

表1 不同划分方案情况下平均BWP指标和均衡性指标β的计算结果Table 1 Calculative average BWP index and equilibrium index β for different partition schemes

通过采用改进的K-means聚类算法将含28座变电站的供电区域合理地划分为若干小规模的供电块，供电块内的变电站间具有非常紧密的联系，同时供电块间变电站之间的联络相对较为薄弱。鉴于此特性，重点对各个供电块开展配电系统的网络结构优化规划将会以最有效、最便捷的路径达到满足整个地区配电系统的精益化规划的需求。

图7 某地区远景期供电块最佳划分方案示意图Fig.7 Schematic diagram of optimal power-supplying block partition scheme planned for a region

4 结论

为了进一步提高配电系统网络结构优化规划的效率及精细化程度，本文以聚类分析思想为基础，提出了基于改进K-means聚类算法的供电块划分方法，主要工作如下：

a.从初始聚类中心的选取和最佳聚类划分数的确定这2个方面对传统的K-means聚类算法进行改进；

b.在透彻分析供电块划分与平面点的划分间差异性的基础上，以变电站圆形供电模型为基础，提出了不同负荷密度下等效半径的折算方法，同时定义了变电站界间距等概念，将供电块的划分问题由平面点的划分转化为面积域的划分；

c.将改进的K-means聚类算法应用到变电站供电块的划分中，建立了基于改进K-means聚类算法的供电块划分的详细流程，最后通过实际算例验证了本文所提方法的科学性和合理性。