LLC谐振变换器软开关边界理论及最小死区设计

张澧生

LLC谐振变换器软开关边界理论及最小死区设计

张澧生

0　引　言

LLC谐振变换器是最适合设计恒定输出电压型开关电源的电路之一，并且得到了国内诸多学者的广泛分析与研究[1-15].这些研究可以归纳为以下几类：变换器设计方法的研究[1-2]、输出端同步整流方案的研究[3-4]、变换器效率优化策略的研究[5-6]、过流保护机制的研究[7]、数字控制型LLC谐振变换器的研究[8]、三电平LLC谐振变换器的研究[9]，以及软开关实现条件方面的研究[10-15]等.

LLC谐振变换器工作时，为了避免出现同一桥臂的上、下两个开关管出现同时导通造成输入侧短路的故障，变换器的控制芯片需要维持有效关断信号直到同一桥臂的另一个开关管完全关断.因此，在一个开关周期内就会出现上、下两个开关管同时关断的时间间隔，这个时间间隔就称之为死区时间.为了实现原边开关管的软开关工作，变换器需要工作在感性工作区，而且谐振网络的谐振电流必须足够大以确保在死区时间内完成对原边开关管和副边整流二极管寄生电容的充分充放电[16].另一方面，为了减小开关管的导通损耗，谐振电流的幅值需要尽量小，但这会导致变换器在轻载或空载工作时，开关管无法工作在软开关状态，从而增加器件的开关损耗.

目前国内外已有少数文献报道了LLC谐振变换器的软开关实现条件[10-15].文献［10］和文献［11］均提出了LLC谐振变换器的软开关实现条件，即在死区时间内完成对金属-氧化物半导体场效应晶体管（简称金属半场效应晶体管）MOSFET（M etal-Oxide-Sem iconductor Field-Effect Transistor，MOSFET）寄生电容的充放电，并进一步提出了最优谐振网络参数的设计思路；然而这些研究均忽略了副边整流二极管对死区时间内变换器换流过程的影响.因此导致设计的充放电电荷需求量要小于实际所需的充放电电荷需求量.文献［12-14］报道了LLC谐振变换器的优化设计策略，并提出了最优励磁电感的设计思路；然而这些研究所得到的结论是建立在死区时间内谐振电流保持不变的假设条件下，而死区时间内，实际的电流波形是呈现正弦变化的，因此所得到的软开关实现条件在精确性上有较大欠缺.文献［15］考虑了副边整流二极管对死区时间内的换流过程的影响，并提出了更精确的最优励磁电感设计方法；然而，该分析仅仅针对开关频率在谐振频率附近的情况，并未针对最差工况进行死区时间设计，所得到的最佳死区时间无法满足全输入电压和全负载变化范围内变换器均能实现软开关的工作需求.

总结已有的文献报道可以发现，已有的关于LLC谐振变换器实现软开关的研究还存在明显不足.为此，本文在第1节中对死区时间内变换器的工作机制进行了深入研究，在考虑副边整流二极管寄生参数的基础上，建立了死区时间内变换器的精确等效模型.基于所建立的等效模型，本文在第2节中提出了变换器的软开关边界理论.根据死区时间内电荷供给量与电荷需求量之间的平衡关系，以及死区时间与电流回零时间的大小关系，可以将变换器的工作状态分为4个工作区域，并归纳得到软开关边界曲线.本文在第3节中进行了最小死区的分析，最小死区即为变换器在最差工况下实现软开关所需要满足的死区时间的最小值.进一步地，本文进行了变换器最差工况下的时域分析，并推导得到了最小死区的数学表达式：实际设计变换器时，死区时间需要大于或等于最小死区时间，即可实现全设计输入电压范围和全设计负载范围内的软开关工作.最后，在第4节中本文结合一款300W样机，进行了理论设计和实验验证.

1　死区时间内变换器的精确等效模型

LLC谐振变换器的电路结构如图1所示，图中Q1—Q4这4个MOSFET构成了原边逆变桥，Dj1—Dj4分别为Q1—Q4的反并二极管；D1—D4整流二极管构成了副边整流桥；Lm、Lr和Cr分别为励磁电感、谐振电感和谐振电容，这3个元件构成了LLC谐振变换器的谐振网络；Cin和Cout分别为输入电容和输出电容；Vin和Vout分别为输入电压和输出电压；Rout为输出等效负载；Ir为谐振电流，Im为励磁电流，Irec为整流桥输出电流，Iout为负载电流；VC为谐振电容两端电压.r

图1　LLC谐振变换器电路图Fig.1　Circuit of LLC resonant converter

为了获得死区时间内变换器精确等效模型，先做如下假设：

（1）MOSFET、整流二极管、谐振电感、谐振电容和线路等原件的串联寄生电阻和寄生电感参数均忽略不计.

（2）MOSFET 的寄生电容等效为电容量随输入电压变化而变化的非线性电容.

（3）副边整流二极管的寄生电容等效为电容量恒定的电容.

（4）输出电压等效为电压源.

由于死区时间内的换流主要是谐振电流对MOSFET和整流二极管寄生电容的充放电，寄生电阻和寄生电感的作用微乎其微，因此在分析等效模型时，忽略它们的影响是可行的.根据MOSFET供应商提供的资料手册不难发现，MOSFET的寄生电容的电容量不是一个常量，输入电压越高，电容量越小，两者之间的关系曲线呈现非线性特征.因此，将MOSFET的寄生电容等效为电容量随输入电压变化而变化的非线性电容是合理的.考虑到死区时间占整个开关周期的比例很小，因此输出电压在死区时间内可以认为是保持不变的，即输出Vout等效为电压源.而对于整流二极管的寄生电容而言，由于输出电压是恒定的，因此寄生电容的电容量也是恒定的.在上述4条假设的基础上，建立死区时间内变换器的精确等效电路，如图2所示.图中Cj1—Cj4为Q1—Q4的寄生电容，Cd1—Cd4为D1—D4的寄生电容，其余符号定义与图1相同.

2　LLC谐振变换器的软开关边界理论

在设计LLC谐振变换器时，一般将其设计在增益放大区，即开关频率小于谐振频率的工作范围内.变换器在该区域内工作时，其典型工作波形如图3所示.图中的Vgs1，3和Vgs2，4分别为Q1，3和Q2，4管的驱动信号；Vds1，3和Vds2，4分别为Q1，3和Q2，4管的漏源电压.

图2　死区时间内变换器的精确等效电路Fig.2　Precise equivalen t circuit of converter during dead-tim e

图3　变换器典型电流波形Fig.3　Typ ical current waveform s of the converter

定义：tdead为死区时间；θ0为电流回零相位；t0为电流回零时间，且满足t0=θ0/ωr；Qc为电荷需求量；Qs为电荷供给量.根据图2所示的等效模型，可以得到

LLC谐振变换器一般使用MOSFET作为开关管.MOSFET实现软开关的前提条件是，驱动信号到来前，寄生电容两端电压已经下降到0.根据电荷供给量与电荷需求量之间的平衡关系，以及电流回零时间与死区时间的大小关系，可以将变换器分为4个工作区域，其分布图如图4所示.下面对每个工作区域的工作原理进行详细分析.

区域A［t0＜tdead，Qs＞Qc］.谐振电流Ir过0时刻，开关管Q2和Q4的漏源电压已经下降到0，反并二极管导通.但由于死区时间还未结束，谐振网络维持谐振，导致死区时间内电流反向，Dj2和Dj4截止.由于驱动信号还未到来，谐振电流再次对Cj2和Cj4充电，使得电压不断上升，软开关工作条件被破坏.当驱动信号到来时，Dj2和Dj4两端电压已经不为0，此区域为非软开关工作区域.

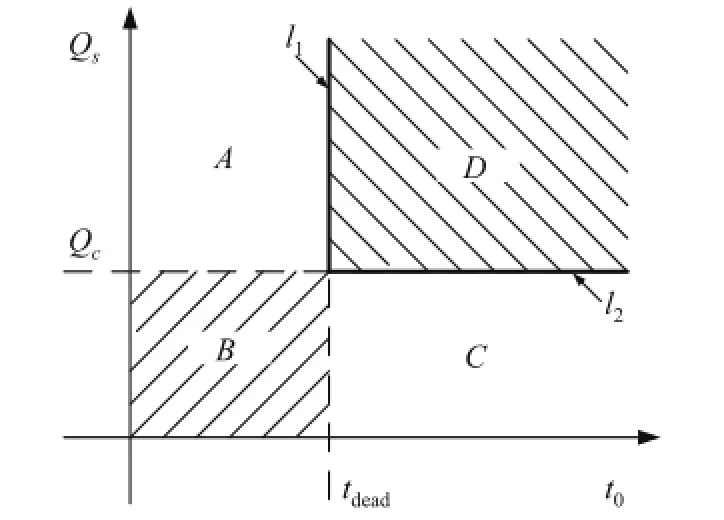
图4　工作区域分布图Fig.4　Distribu tion figure of operation region

区域B［t0＜tdead，Qs＜Qc］.谐振电流Ir过0时刻，开关管Q2和Q4的漏源电压还未下降到0.t0＜t＜tdead时间段内，谐振网络的工作状态与区域A的相同，漏源电压还未下降到0就被再充电，无法创造软开关工作条件.因此该区域也为非软开关工作区域.

根据上述分析，LLC谐振变换器的软开关工作区域为区域D，其余为非软开关工作区域，两者之间的分界线为射线l1和射线l2（如图4中粗实线所示）.因此这两条射线构成了LLC谐振变换器的软开关边界曲线，并且l1和l2可以分别表示为式（3）和式（4）.

3　LLC谐振变换器的最小死区设计

LLC谐振变换器能够通过改变开关频率的调制方式实现高效率功率变换，同时产生极小的电磁干扰.为了实现上述目标，确保变换器在最差工况下也能实现软开关是一个非常重要的研究课题.对于一组确定的谐振网络参数，死区时间的长短直接决定了变换器能否顺利实现全设计输入电压范围和全设计负载范围内的软开关工作.为了确定所需的死区时间，必须考虑实现软开关所需的最小死区时间以确保最差工况下变换器也能工作在软开关状态.该最差工况发生在设计空载条件下，而且此时施加在变换器的输入电压为最高电压[16].下面给出最差工况的时域分析与最小死区时间的推导过程.

最差工况下的等效电路图和工作波形分别如图5和图6所示.图中Vinmax为最高输入电压，Tswmin为最小开关周期（对应的fswmax为最大开关频率）.

图5　最差工况下等效电路图Fig.5　Equivalent circuit under the worst case

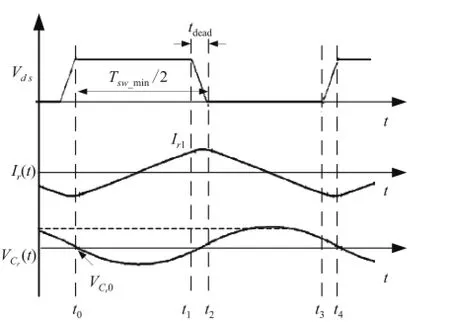
图6　最差工况下工作波形Fig.6　Operationalwaveform s under the worst case

t0—t1时间内，变换器等效电路如图5（a）所示，列写状态方程可以得到

对上式进行Laplace变换可得

其中，Ir（s）和VCr（s）分别为Ir（t）和VCr（t）的复频域形式.

从式（6）中可以得到，Ir（s）和VCr（s）可以分别表示为

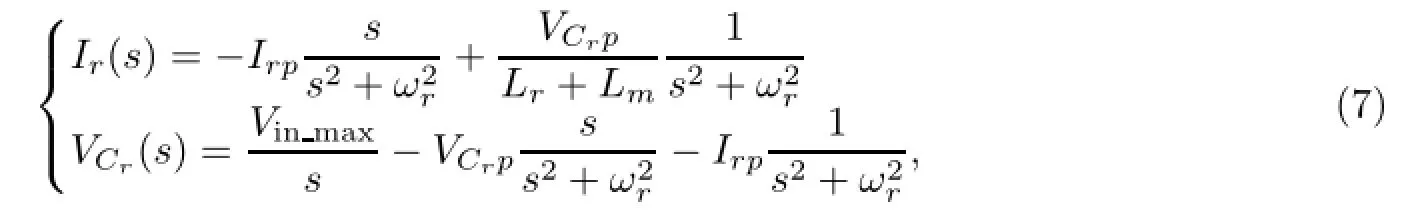
因此，谐振电流和谐振电容两端电压的时域表达式可以表示为

其中，Irp为谐振电流幅值；VCrp为谐振电容两端电压幅值；Zm为变换器的空载特征阻抗，可以表示为

根据图2所示的死区时间内的等效电路图，列写回路方程得

因此可得

根据式（12）和图2，可以发现，死区时间内原边逆变桥可以等效为MOSFET寄生电容两并两串的结构.同理，副边也可以等效为整流二极管寄生电容两并两串的结构.因此图2可以进一步简化为图5（b）.这里假定MOSFET寄生电容的电容量是相同的，均为Cj，整流二极管寄生电容的电容量均为Cd.为了满足软开关工作要求，死区时间需要满足

在图6中，我们注意到，谐振电容两端电压的稳态平均值为0.变换器一般满足（Cj+，因此谐振电容初始电压满足

将式（15）代入式（14），化简得

其中，电流相位角满足φ=π·fr·Tswmin=π·fr/fswmax.式（16）的另一种形式为

实际中，一般ωrtdead＜＜1，再结合Ir（t1）=Ir1=Irp，将式（18）代入式（13）可得最小死区时间t dead m in满足

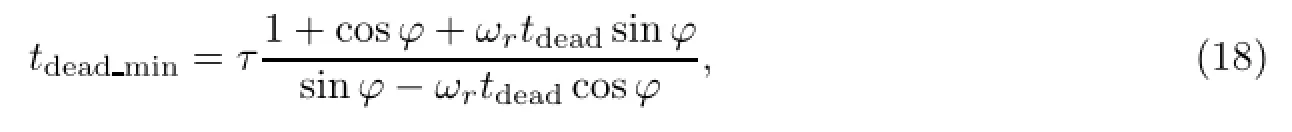
式（19）有两个解，表示为

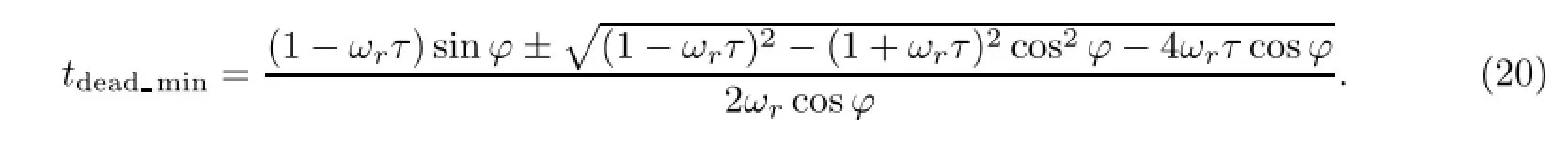
将式（21）代入式（20），进一步化简得

一般fswmax＜2fr，即φ＞π/2，所以tanφ＜0.因此式（22）中有一个解可以排除，最小死区时间表示为

根据软开关边界条件要求，此时的电荷供给量需要大于电荷需求量，因此有

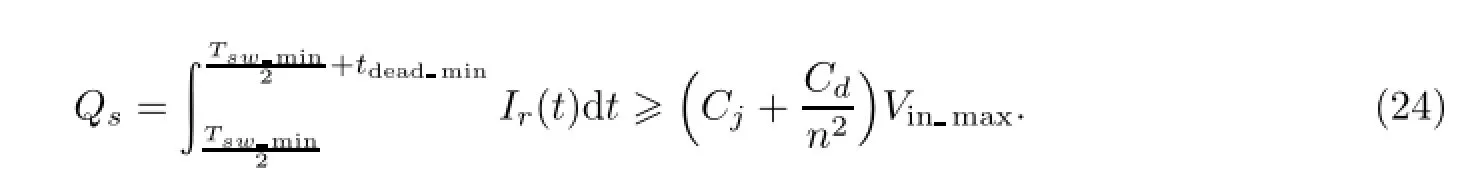
推导可得

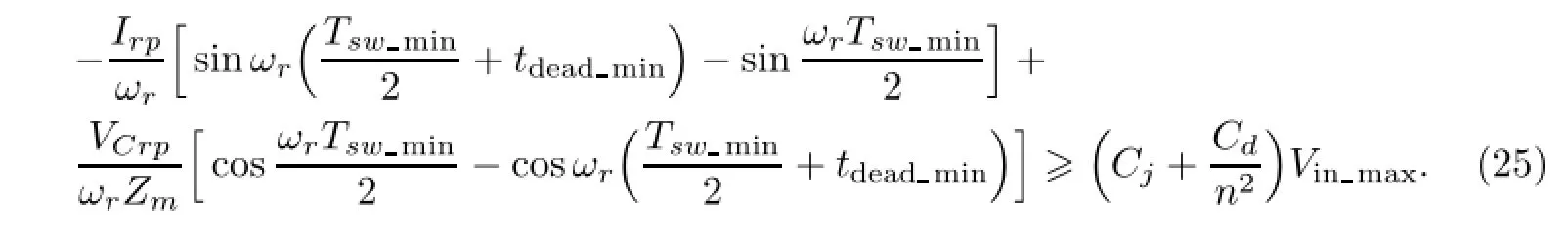
当设计最高输入电压对应的工作点为谐振点时，即满足fswmax=fr，可以进一步简化式（25）.结合VCrp=Vinmax-VCr0，以及式（15）和式（17），化简可得

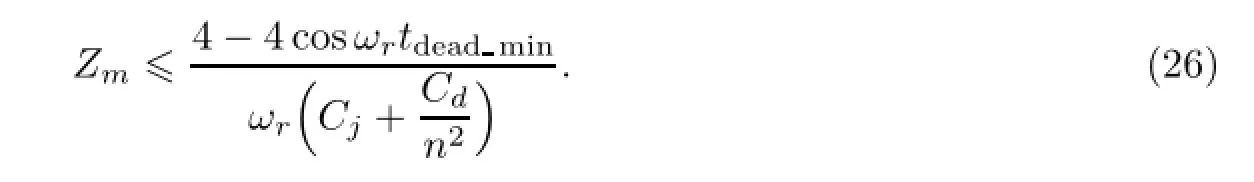
为了实现全输入电压范围和全负载范围内的软开关工作，最小死区时间按照式（23）设计，同时要求特征阻抗满足式（26）.

4　实例及其验证

4.1实例及其设计过程

为了验证所提出的理论的准确性，本文设计了一台300W的LLC谐振变换器样机，其输入电压为30—60 V，输出电压为380 V.MOSFET选用IPP 075N 15N3，最大输入电压下对应的寄生电容为750 pF；整流二极管选用MUR860，380 V输出电压下对应的寄生电容为20pF.按照文献［11］提到的可行性设计方法，设计过程分为以下4步.

第1步：设计励磁电感值Lm.根据输出功率Pout、谐振频率fr和死区时间tdead，电流角取2倍裕量[11].然后可以根据公式（27）计算出励磁电感值Lm.输出功率Pout为300W，谐振频率fr选取为100 kHz，死区时间tdead选取为300 ns，励磁电感电感值的计算结果为48 uH.公式（27）是

第2步：设计谐振电感值Lr.根据经验，一般将电感比h（如式（28）所示）设计为3—8，这里选取h为4，将励磁电感值代入公式（28）得谐振电感值Lr为12 uH.公式（28）是

第3步：判断最大增益是否达到实际要求.针对最小输入电压满载输出工况，在仿真软件中进行仿真分析，若最大增益满足不了要求，则减小励磁电感值Lm，直至满足设计要求.本设计中，最大增益达到2.25，对应的开关频率为53.3 kHz，最大增益满足实际要求，因此不需要减小励磁电感值Lm.

第4步：完成初步设计.将谐振频率fr和谐振电感值Lr代入公式（29）得到谐振电容值Cr，选取最接近的电容值，这里为220 nF.公式（29）是

设计的谐振网络参数为：励磁电感值Lm=48 uH；谐振电感值Lr=12 uH；谐振电容值Cr=220 nF；对应的初始死区时间tdead=300 ns.

将上述谐振网络参数代入式（23）计算得到最小死区时间为159 ns.代入式（26）计算得到最小死区时间下的临界特征阻抗为19.93Ω.将Lm、Lr和Cr的值代入式（10）得此时的特征阻抗为16.51Ω.满足式（26）要求的软开关实现条件，可见该设计是合理有效的.

4.2实验验证

实验样机的主要元器件及参数为：变压器匝比为0.157（原边8匝，副边51匝）；变压器和谐振电感均用PC40磁芯，骨架分别为PQ 35/35和PQ 20/20；绕制好的变压器，实测励磁电感值为48.2 uH，实测谐振电感值为12.1uH；谐振电容选用EACO的薄膜电容，2×100 nF+22 nF.

图7所示为验证最小死区设计有效性的实验波形.图7（a）为tdead=160 ns时的实验波形.图中Vds4为Q4管漏源电压，Vgs1和Vgs4分别为Q1和Q4管的驱动电压，Ir为谐振电流.从图7（a）和7（b）中可以看出，在死区时间结束时，开关管寄生电容两端电压恰好下降到0，变换器工作在软开关状态.为了验证理论分析的准确性，将死区时间分别变化到300 ns和100 ns，得到的死区时间内实验波形分别如图7（c）和7（d）所示.从图7（c）中可以看出，死区时间内，开关管寄生电容两端电压已经下降到0并且维持，直到驱动信号到来，变换器工作在软开关状态.而图7（d）中，可以明显看出，死区时间内电压的下降不是线性的，而是有明显的转折点，这个转折点对应的时间即为死区时间结束时刻.由于无法创造软开关工作条件，驱动信号到来时，变换器的漏源电压出现震荡，变换器工作在非软开关工作状态.

图7　最差工况下实验波形Fig.7　Experimentalwaveform s under the worst case

为了验证变换器的软开关工作特性，在全输入电压范围和全负载范围内分别按输入电压和输出负载各选取10个点，形成一个10×10的测试表格，共100个测试点.实验过程发现，变换器在这100个测试点下均能实现软开关工作.图8为4种极端工况下的试验波形：图8（a）为最低输入电压下的空载实验波形，此时的开关频率为59.2 kHz；图8（b）为最低输入电压下的满载实验波形，开关频率为52.6 kHz；图8（c）为最高输入电压下的空载实验波形，开关频率为99.3 kHz；图8（d）为最高输入电压下的满载实验波形，开关频率为97.3 kHz.

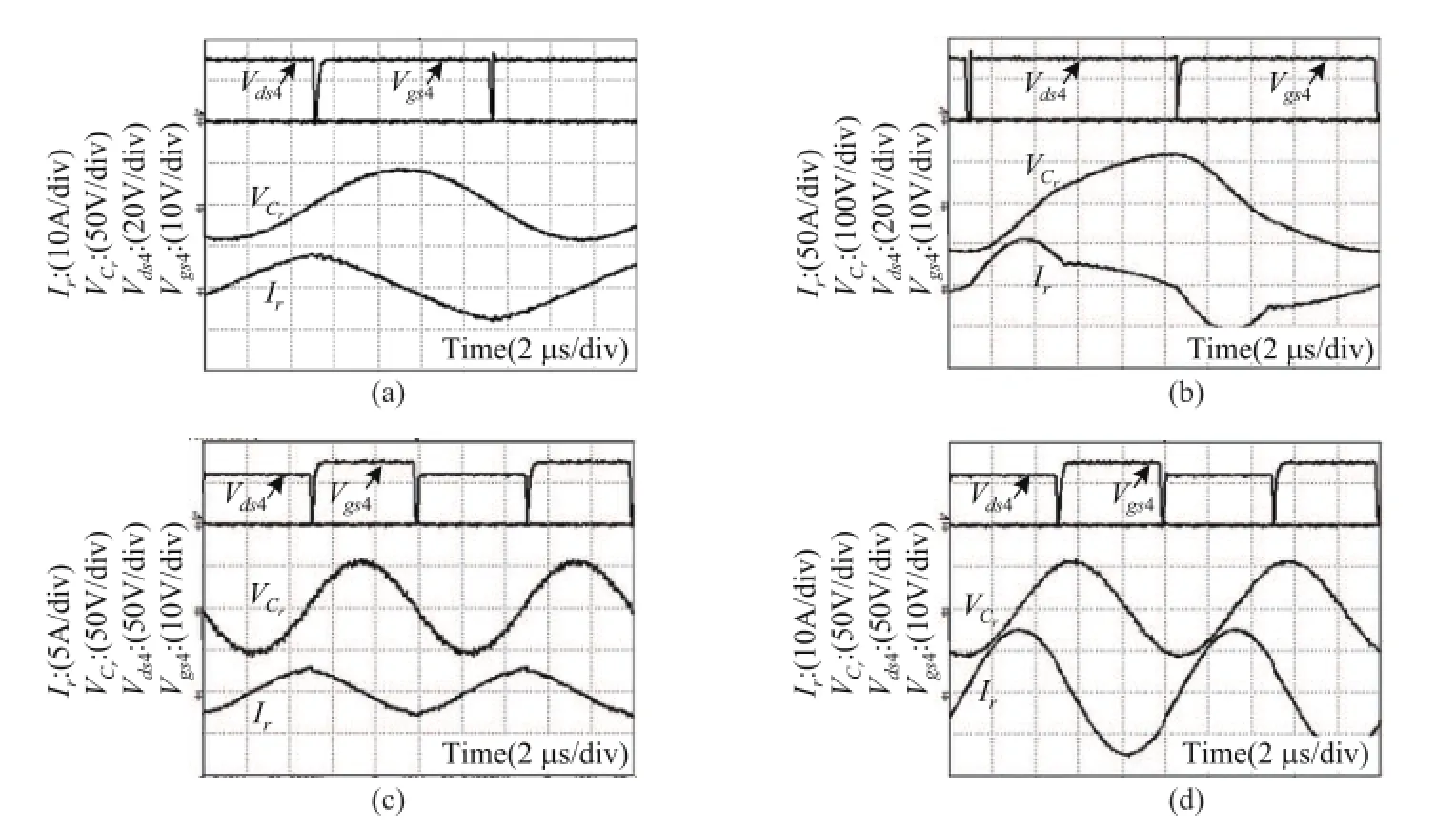
图8　极端工况下实验波形Fig.8　Experimentalwaveform s under extreme case

图9显示了本文所提出的方法（死区时间为160 ns）与文献［11］提到的传统设计方法（死区时间为300 ns）在效率特性上的差别.图9（a）为最高输入电压60 V下，两组参数的效率对比曲线.由图可见，本文所提出的方法在满载工作时的效率为96.39%，而传统设计方法为95.53%，死区时间优化后，效率可以提升0.86%.全负载范围内效率提升均在0.5%以上. 图9（b）为最低输入电压30 V下，两组参数的效率对比曲线.由图可见，本文所提出的方法在满载工作时的效率为94.91%，而传统设计方法为94.42%，死区时间优化后，效率可以提升0.49%.全负载范围内效率提升均在0.44%以上.可见，本文所提出的死区时间优化方法，在不改变谐振网络参数的基础上，可以进一步提高变换器工作效率.

图9　极端工况下实验波形Fig.9　Com parison of efficiency curve

5　结论

本文以LLC谐振变换器的软开关工作特性为研究对象，分析了死区时间内变换器的工作原理，并建立了死区时间内变换器的等效模型.该模型考虑了原边开关管寄生电容的非线性特性，同时还考虑了副边整流二极管的寄生电容对死区时间内换流的影响，因此更加精确.在等效模型的基础上，本文提出了变换器的软开关边界理论，并归纳得到了软开关边界曲线.该理论认为在全输入电压和全负载范围内，变换器可以分为4个工作区域，其中有3个为非软开关工作区域，是需要在设计过程中避免的.最后，本文分析了确保变换器在最差工况下也能实现软开关的最小死区，并推导了最小死区的数学表达式.理论与实验的吻合验证了理论分析的准确性.本文所做工作进一步丰富了LLC谐振变换器的分析理论，并且可以为软开关工作特性分析和死区时间优化提供科学指导.

[1］马皓，祁丰.一种改进的LLC变换器谐振网络参数设计方法[J].中国电机工程学报，2008，28（33）:6-11.

[2］肖文英，董海兵.全桥LLC谐振变流器的简化时域模型及其应用[J].华东师范大学学报:自然科学版，2013（5）:119-129.

[3］X IE X F，CHU I J，LIU P，et a l.A nove l h igh frequen cy cu rren t-d riven syn ch ronous rec tifier app licab le to m ost sw itching topologies[J].IEEE Trans Power E lectron，2001，16（5）:635-648.

[4］FU D B，LIU Y，LEE F C，et a l.A nove l d riv in g schem e fo r syn ch ronous rectifiers in LLC reson an t conver ters [J].IEEE T rans Pow er E lect ron，2009，24（5）:1321-1329.

[5］赵晨，石洋，吴新科，等.三元件串联LLC谐振变流器的优化设计策略[J].电工技术学报，2008，23（1）:65-71.

[6］郭稳涛，何怡刚.基于复形法的LLC谐振变换器最优设计方法及其实现[J].华东师范大学学报:自然科学版，2013（3）: 176-185+218.

[7］X IE X G，ZHAO Z，ZHAO C，et a l.Analysis and op tim iza tion o f LLC resonan t converter w ith a novel overcu rren t p rotection circuit[J].IEEE T rans Pow er E lectron，2007，22（2）:435-443.

[8］GROO T H，JANSSEN E，PAGA NO R.，et a l.Design o f a 1-M H z LLC resonan t conver ter b ased on a DSP-d riven SO I ha lf-b ridge p ow er M OS m odu le[J].IEEE Trans Pow er E lec tron，2007，22（6）:2307-2320.

[9］GU Y L，LU Z Y，HANG L J，et a l.Th ree-leve l LLC series resonan t DC/DC conver ter[J].IEEE T ran s Pow er E lec tron，2005，20（4）:781-789.

[10］郭稳涛，何怡刚.一种改进的谐振型通信电源设计方法——基于时域限制条件的LLC谐振变换器设计[J].电源技术，2012，36（12）:1925-1927+1937.

[11］ZHANG X，YOU W，YAO W，et a l.A n im p roved design m ethod o f LLC resonan t converter[C]//ISIE，12.N ew York:IEEE P ress，2012:166-170.

[12］LU B，LIU Y，LEE F C，et al.Op tim a l design m ethodology for LLC resonan t converter[C]//APEC，06.New York:IEEE Exp ress.2006:533-538.

[13］T heo retica l ana ly sis an d op tim a l design o f LLC reson an t conver ter[C]//Pow er E lec tron ics and A pp lications. New York:IEEE E xp ress，2007:1-10.

[14］Dynam ic ana lysis and op tim al design of high efficiency fu ll b ridge LLC resonan t converter for server power system[C]//APEC，12.New Yo rk:IEEE Exp ress，2012:1292-1297.

[15］LEE J Y，JEONG Y S，HAN B M.A n iso lated DC/DC conver ter u sing h igh-frequen cy un regu la ted LLC resonant conver ter fo r fue l ce ll ap p lications[J].IEEE T ran s Pow er E lect ron，2011，58（7）:2926-2934.

[16］BE IRANVAND R，RASH ID IAN B，ZOLGHADR IM，et a l.Design ing an ad justab lew ide range regu la ted cu rren t sou rce[J].IEEE Trans Power E lectron，2010，25（1）:197-208.

（责任编辑李艺）

（湖南机电职业技术学院 电气工程系，长沙410151）

LLC谐振变换器已经在开关电源领域得到了广泛应用，但现有的关于变换器软开关实现条件及死区时间设计的研究还存在明显不足.为此，本文以LLC谐振变换器软开关工作特性为研究对象，建立了死区时间内变换器的精确等效模型，并在此基础上提出了变换器的软开关边界理论.该理论根据死区时间内电荷供给量与需求量的平衡关系，以及死区时间与谐振电流回零时间的大小关系，将变换器工作区域分为一个软开关工作区域和三个非软开关工作区域，并归纳得到了软开关边界曲线.分析了变换器在最差工况下也能实现软开关的最小死区，并推导得到了最小死区的数学表达式.最后，结合一款300W的样机进行了实例验证，理论设计与实验结果的吻合验证了理论分析的准确性.

LLC谐振变换器；软开关；死区时间；最差工况

Boundary theo ry of soft sw itching and m in im um dead-tim e design for LLC resonan t converter

ZHANG Li-sheng
（Department of Electrical Engineering，Hunan Mechanical and Electrical Polytechnic，Changsha410151，China）

LLC resonan t converter is w idely used in sw itched m ode power supp lies. However，the p resent research on conditions of realizing soft sw itching and the design of dead tim e has obv ious shortcom ings.Therefore，the soft sw itching of LLC resonant converter is studied，and the soft sw itching boundary theory is proposed based on the p recise equivalent m odel du ring the dead-tim e interval.Accord ing to the balance between the supplying charge during the dead-time and the required charge，together w ith the length relationship between the dead-tim e and the zero-crossing tim e of resonant cu rrent，the operation region of the converter can be divided into one soft sw itching operation region and three hard sw itching operation region，and the boundary cu rve of soft sw itching is concluded.The m inimum dead-time for realizing soft sw itching even under the worst case is analyzed，and the m athem atical equation of the m inim um dead-tim e is derived. Finally，a 300 W p rototype is build，and the accuracy of the theory is verified by theaccordance between the theoretical design and the experimental results.

LLC resonant converter；soft sw itching；dead-time；worst case

TM 46

A

10.3969/j.issn.1000-5641.2015.06.012

1000-5641（2015）06-0090-11

2014-1

湖南省科技计划资助项目（2013FJ6041）；湖南省教育厅资助科研项目（12C1066）

张澧生，男，硕士，副教授，主要研究方向为电力系统电能质量优化、电力电子技术等. E-mail：zls hnjd@163.com.