一种新的自适应惩罚函数在遗传算法中的应用
蔡海鸾,郭学萍
(1.华东师范大学 数学系,上海 200241;2.华东师范大学 上海市核心数学与实践重点实验室,上海 200241)
一种新的自适应惩罚函数在遗传算法中的应用
蔡海鸾1,2,郭学萍1,2
(1.华东师范大学 数学系,上海200241;2.华东师范大学 上海市核心数学与实践重点实验室,上海200241)
惩罚函数是遗传算法中解决非线性约束最优化问题最常用的方法之一.但传统的惩罚函数运用到遗传算法中往往难以控制惩罚因子,因此本文引进了一种结构简单、通用性强的新自适应惩罚函数,并证明了其收敛性.随后构建了基于新自适应惩罚函数的遗传算法,使得种群能快速进入可行域,并且提高了遗传算法的局部搜索能力.理论分析及仿真结果表明该算法具有参数少、稳定性强、收敛快等优点.
约束最优化;惩罚函数;遗传算法;自适应惩罚函数
0 引 言
非线性约束优化问题是优化问题中最复杂的问题之一,而遗传算法是约束优化中运用最为广泛的一种算法.它以生物模型为原型,快速地搜索出解空间中的全体解,而不会陷入局部最优解的快速下降陷阱之中[1],并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度.但是遗传算法的局部搜索能力较差,导致单纯地运用遗传算法比较费时,从而使得在进化后期搜索效率较低[1].在实际应用中,遗传算法容易产生早熟收敛[2].如何既保留优良个体,又维持群体的多样性,一直是遗传算法中较难解决的问题.早期人们提出用惩罚遗传算法来提高种群的适应度,很好地解决了遗传算法的适应度问题[3],但是新的问题是,惩罚函数的惩罚系数往往难以控制,过大或过小都会导致算法病态[4].因此提出一种新的自适应惩罚遗传算法来解决约束优化问题.根据当前群体中的可行解的比例对目标函数和违反约束条件的程度作出一个合适的权衡,使得种群快速进入可行区域,提高遗传算法的局部搜索能力.
1 传统的惩罚函数
惩罚函数是将约束条件的违反度作为惩罚项加到目标函数中,从而构造出带参数的增广目标函数.其思想是把一系列的约束优化问题转化成无约束的优化问题求解.在新的目标函数中,惩罚因子的不断变化,导致最优解也不断变化,最终趋于原问题的最优解.非线性约束优化问题一般可表示为[5]
使得
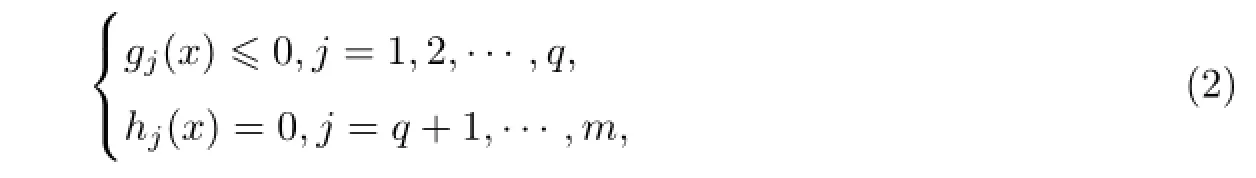
其中,f(x)为目标函数,gj(x)和hj(x)分别为不等式约束条件和等式约束条件,x∈Ω⊆S. S⊆Rn是搜索空间,Ω是可行域,即满足所有约束条件的空间.
惩罚函数方法即把问题(1)转化为:m in G(x)=f(x)+cφ(x).其中,G(x)悱做惩罚函数,c为惩罚因子,φ(x)称为惩罚项.
一般地,惩罚项是基于个体到可行域的距离.个体x到第j个约束条件的距离可以表示为:

引理1.1[4]假设f,g,h是Rn上的连续函数,又设对于每一个c,都有一个xc∈Rn,使得θ(c)=f(xc)+cφ(xc)成立,则
(1)inf{f(x):g(x)≤0,h(x)=0}≥supc>0θ(c),其中θ(c)=in f{f(x)+cφ(c)};
(2)当c>0时,f(x)关于x单调不降,θ(c)关于c单调不降,φ(xc)关于c单调不增.
惩罚函数方法可以直接利用无约束最优化问题的算法来求解原约束最优化问题,因此有简单实用等优点.由于惩罚函数方法在每一迭代步不涉及可行方向和投影的计算,因此惩罚函数方法更适合求解非线性约束优化问题.虽然惩罚函数方法能简单有效地解决非线性约束最优化问题,但是惩罚函数方法在迭代过程中有时要求惩罚因子趋于无穷大,从而使得子问题越来越病态,并且惩罚函数方法的收敛速度也很慢.在遗传算法中惩罚函数是处理非线性约束优化最常用且最有效的一种方法,因此本文构造一种新的自适应惩罚函数来处理遗传算法的约束条件.
2 新的自适应惩罚函数
综合各种观点,要设计一个好的惩罚函数处理遗传算法的约束条件有以下原则[3]:
(1)结构简单,参数尽可能的少;
(2)能在进化过程中正确权衡目标函数和障碍函数.
考虑一般线性约束规划问题(1),可以构建如下形式的惩罚函数[3]:

由惩罚函数的设计原则知,只需对式(3)的惩罚系数c进行设计.下面分析在约束过程中c应该如何变化.
在优化过程中的早期,群体中没有或只有少量的可行解,这时,c应该是相对大的值,以引导搜索进入可行解区域.随着进化的进行,一些可行解将进入群体,这时,惩罚应该逐渐减小.而且,可行解越多,惩罚应该越小,因此c应随着可行解的比例(ρ)的增大而逐渐减小.从而使得搜索策略的重心从搜索可行解转移到搜索好的目标函数上来.同时,也可以让有较小目标函数值和较小违法约束条件的非可行解进入群体,这对于求解最优解在可行域与不可行域的边界上的约束规划问题非常重要.当群体中全部是可行解时,惩罚系数c减到最小值0.
从上面分析可以得出:惩罚系数c在优化过程中的变化依赖于当前群体可行解的比例.记当前可行解的比例为ρ,那么系数c可以表示为ρ的函数c(ρ).ρ代表可行解的比例,ρ越大表示可行解越多,c应该越小,因此c(ρ)是一个减函数.
设计的主要问题是寻求满足以上性质的惩罚系数c(ρ),综合各种性质,本文设计函数c(ρ)为

其中,α>0是一个需要调整的参数,具体可取[0,10]之间的一个整数.基于我们设计的c(ρ),构建如下新的惩罚函数:

新的惩罚函数有如下性质:
(1)c(ρ)随ρ的增大而减小,c(ρ)是一个减函数.
(2)惩罚系数c(ρ)的初始值是随群体中的可行解的比例ρ变化而变化的.如果初始群体中可行解的比例较大,那么c(ρ)的值就较小,反之较大.在优化的过程中我们并没有强加给c(ρ)一个小的或者大的初始值,而是随种群当前状态所决定.
(3)当ρ=0时有最大值c(0)=10α-1,这时群体没有可行解,惩罚系数达到最大,引导搜索进入可行区域.
(4)当ρ=1时有最小值c(1)=0,这意味着都是可行解,惩罚系数最小,非常有利于非可行解进入群体.
(5)在从0到1变化的早期过程中,惩罚系数急剧减小,一段时间后则缓慢减小.这可使得搜索重心从可行解快速地转移到目标函数上来.
(6)在整个优化过程中惩罚系数不会过大或过小,可以看出这是动态的自适应的.
若新构造的自适应惩罚函数是收敛的,则新自适应惩罚函数处理约束条件是有效的[7].下面分析新自适应惩罚函数的收敛性.
定理2.1(新自适应惩罚函数的收敛性)考虑问题(1),其中f,g,h是Rn上的连续函数,假设此问题有一个可行解,此外对于每个α,无约束最优化问题m in G(x,α),存在一个解xα∈Rn,其中xα包含在Rn中的紧子集中,则
(1)inf{f(x):g(x)≤0,h(x)=0}=supα≥0θ(α)=limα→∞θ(α);
(2)xα的任一收敛子列的极限值x∗是问题(3)的最优解,并且当α→∞时,[10α(1-ρ)-1]φ(xα)→0.
证明由引理1.1的(2)知θ(c)是关于c的单调不降的函数.又由于c=10α(1-ρ)-1是关于α的单调增函数,由复合函数的性质知,θ(α)是关于α的单调不降函数,由极限的单调有界定理[8],可知supα≥0θ(α)=limα→∞θ(α).下证α→∞时φ(xα)→0.
设问题(1)的惩罚函数m in G(x,α)对α=1的最优解是x1,如果对∀∈>0满足
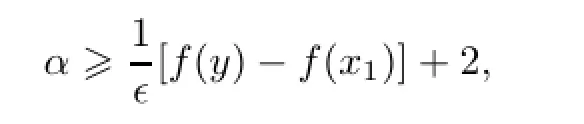
则有f(xα)≥f(x1)(证明过程见文[4],第204页定理10.1.1).
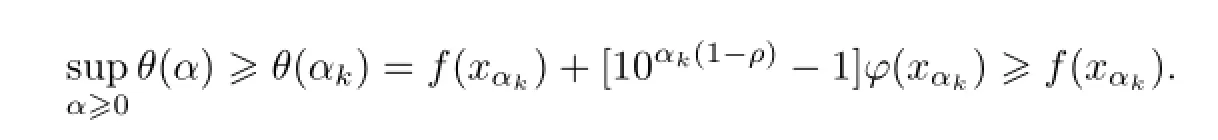

当α→∞时即φ(xα)→0,φ(x∗)=0,这表示x∗是原问题(1)的可行解.由式(5)和引理1.1的(1)知x∗是问题(1)的最优解,并且supα≥0θ(α)=f(x∗).当α→∞时
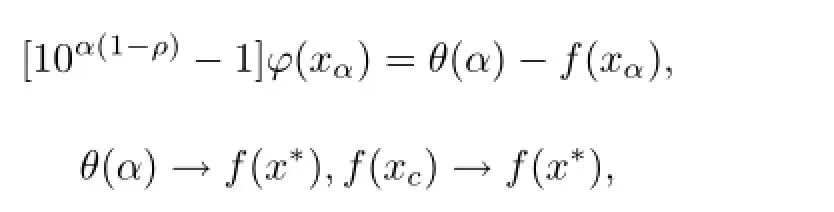
3 基于新的自适应惩罚函数的遗传算法
数值方法求解约束最优化问题的主要手段是迭代运算.一般的数值迭代方法容易陷入局部极小的陷阱而出现“死循环”现象,使得迭代无法进行.遗传算法很好地克服了这一缺点,是一种全局优化算法,但用于控制染色体的遗传算子通常会产生非线性规划的不可行后代,因此解决非线性优化的主要问题是如何处理约束条件.一般有如下几种方法:拒绝方法;修补方法;惩罚函数法.其中惩罚函数法是遗传算法处理非线性约束条件最常用的一种方法,惩罚项可以取常数也可以取变量,常数对于解决复杂的约束优化问题效率比较低,若对每个约束条件都独立给予惩罚因子,目标函数对参数的依赖将会变得非常的强,因此本文采用新的自适应惩罚函数.遗传算法从含有大量个体的初始种群中搜索最优解,通过选择算子把具有较好适应值的个体选择出来,进行交叉变异,然后扩大搜索空间,形成下一代种群.遗传算法中惩罚函数是对任意违反约束条件的个体,乘以一个惩罚项,然后加到进化函数中,使得违反约束的个体的适应度降低,再选择算子,生成下一代种群,从而在种群中保持一定的不可行解,使得遗传算法从可行解和不可行解两个区域进行搜索,找到全局最优解.
3.1适应度函数
遗传算法中使用适应度来度量群体中各个个体在优化计算中有可能达到或接近于最优解的程度.适应度越大的个体遗传到下一代的概率就越大;反之,则概率越小.度量个体适应度的函数称为适应度函数(Fitness Function).适应度函数的设计有以下要求[7]:
(1)单值,非负,连续,最大化;
(2)合理,一致性;
(3)计算量小;
(4)通用性强.
基于以上要求本文选择以下适应度函数:
(1)若目标函数为最小值问题,则

(2)若目标函数为最大值问题,则

由以上适应度函数的构造可知,fitness(x)越大,表明个体越接近最优解.下记xp的fitness(x)为f(xp).
3.2交叉算子
交叉算子一般作用在父代两个个体上,有时也可以作用在两个以上的个体上,它通过融合父代基因型的信息来产生新的子代基因型.根据适应度fitness(x)的大小,用轮盘赌选择算子从种群P(t)(t表示当前种群的代数)中选出n(n为偶数)个父母点(设父母点的集合为P),对每对父母点xi和xj构造新的交叉算子,两个后代按以下方式产生:

3.3变异算子
简单遗传以初始种群为基点,经过选择、交叉、变异等操作生成新的种群,以此更新种群,直到满足终止条件.遗传算法中变异算子的具体操作是以pm为变异概率,用新的基因代替原有的基因,从而产生新的个体.变异算子对个体编码串的基因做了局部改变,维持种群的多样性,有利于防止种群出现早熟现像.
常见的变异算子主要有基本变异、均匀变异以及高斯变异等等(可参考文[7]),从这些变异算子的设计中可以看出变异算子的设计会涉及变异点的位置确定和基因值的替换两方面.综合以上变异操作,为了保证点跳出局部最优,我们做如下变异操作:

其中,r 是[0,1]之间的一个随机数.xj∈p(t+1),uj,lj分别是搜索空间中xj的上界与下界.
3.4基于新的自适应惩罚函数的遗传算法
基于问题(1)本文做出一个详细的研究,算法具体操作如下:
(1)将原约束优化问题(1)转化为无约束优化问题,构建新的自适应惩罚函数
(2)给定搜索精度∈1,∈2,初始化种群大小n及繁殖概率,交叉概率pc,变异概率pm,进化代数t.
(3)计算每一个体的适应度:采用如下函数作为适应度函数

(4)初始化种群:随机生成n个初始值作为初始种群.
(5)自适应产生ρ:初始s=0,若φ(xi)<∈1,则s=s+1,ρ=,获取最优个体x(k).
(7)选择繁殖操作:将种群中的个体按适应度由大到小排序,然后根据单个个体所对应的适应度确定其繁殖后在交配池中所占的比例
(8)产生n个0到1之间的随机数,依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数.
(9)交叉操作:交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某两个个体或两个以上个体的部分染色体.
本例采用第3.2节的交叉方法,其具体操作过程如下:
①对每串产生[0,1]间随机数r,若r<pc,则该串参加交叉操作,如此选出参加交叉的一组后,随机配对.
②对每一对,产生[0,1]间的随机数rij,i=1,2;j=1,2.两个后代按以下方式产生:

(10)变异操作:设变异概率为pm,则每一位基因值以等概率变异.对每一串中的每一位产生[0,1]间的随机数r,若r<pm,则该位发生变异,本文按(3.3)方式进行变异,具体操作如下:

(11)若种群未达到最大进化代数,则转至(3),否则此时种群中适应度最大的个体所对应的目标函数值为全局最优解,输出最优解.
由于算法的收敛性决定算法的有效性,下面分析新自适应遗传算法的全局收敛性.
3.5新自适应遗传算法的收敛性
根据Banach压缩原理,如果能够找到一个合适的度量空间,使得新算法成为一个压缩映射,那么,就可以证明,任意选取初始群体P(0),新算法收敛于某个唯一的不动点x∗,下面具体分析新自适应遗传算法的收敛性.
定义3.1[9]设X是一个非空集合,若d是一个X×X到R的映射,并且对于∀x,y,z∈X满足:
(1)d(x,y)≥0,当且仅当x=y时d(x,y)=0;
(2)d(x,y)=d(y,x);
(3)d(x,y)≤d(x,z)+d(z,y).
则称d为X上的度量,称(X,d)为度量空间.
定义3.2[9]设(X,d)为度量空间,{xn}是度量空间(X,d)中的序列,若∀ε>0,存在一个正整数N,使得对一切m,n>N,有d(xm,xn)<ε,则称序列{x n}是(X,d)中的Cauchy序列,若其中的每一个Cauchy序列都收敛,则称(X,d)为完备度量空间.
定义3.3[10]设(X,d)为完备度量空间,对于映射f:X→X,∃ε∈[0,1),使得对∀x,y∈X,满足:d(f(x),f(y))≤ε·d(x,y),则称f为压缩映射.
定理3.4(Banach压缩映射原理)[10]设(X,d)为完备度量空间,f:X→X为压缩映射,则f有且仅有一个不动点x∗∈X,并且对于∀x0∈X满足:其中
定理3.5(新算法的收敛性)考虑问题(1).设S是所有群体的集合,若存在映射δ:S×S→R,使得(S,δ)是一个完备的度量空间,又设存在映射g:S→S,使得g是压缩映射,则对任意选取的初始群体P(0),新算法都全局收敛于某个唯一的不动点x∗.
证明设P为新遗传算法的一个种群,种群大小为n,即P={x1,x2,...,xn}.种群P的平均适应度函数为:).求解问题(1)的最小值,定义
其中,fm in(P1)是第一代中最小的适应度,M是F 的上确界.
(1)δ(P1,P2)=δ(P2,P1),∀P2,P1∈S;
(2)δ(P1,P2)≥0,∀P2,P1∈S;
(3)δ(P1,P2)+δ(P2,P3)≥δ(P1,P3),∀P2,P1,P3∈S.
因此,(S,δ)是一个度量空间.由于S是有限集合,所以S中的任意Cauchy序列都收敛,那么,(S,δ)是一个完备的度量空间.
根据遗传算法的选择原理[1],F(P(t+1))>F(P(t)),即种群的适应度随着代数的增加而增大.所以,对于映射)使得:

所以,g是一个压缩映射,由Banach压缩映射原理可知,该新的自适应遗传算法收敛于唯一的不动点,即.并且,P∗与初始种群的选择无关.因此,P∗是全局最优解.
4 数值实验
以下给出两组测试函数:

使得
已知最优精确解为x∗=(1,1,1,1,1,1,1,1,1,3,3,3,1),f(x∗)=-15.
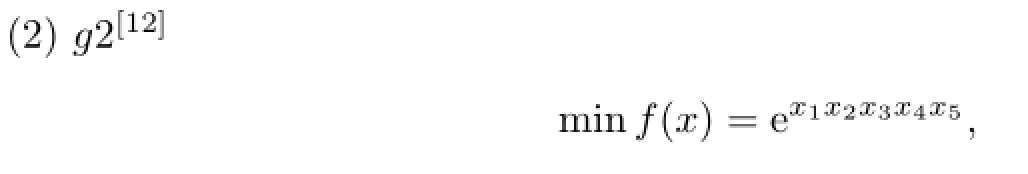
使得

下面是实验结果分析.
数值实验在matlab中完成,运行代数为1 000,每个测试在相同条件下独立运行30次,记录其最优值,平均值,最差的值以及cpu运行时间.本文选取了三种目前较好的最优算法作为比较,文献[12]中的随机排序法(简称RY),文献[13]中的自适应惩罚函数法(简称HW),文献[14]中的静态函数法(简称HF).结果如表1所示.

表 1 新算法与其他算法的结果比较Tab.1 Resu lts com paring our new method with othermethods
根据表1所得数据结果对g1,g2做详细分析.
(1)新算法与RY,FW,HF相比,这几种方法都能得出最优解,但新算法参数显然较RY,HF少.下面对参数的敏感性进行分析.
(2)对参数的敏感性分析如表2.

表 2 参数的敏感性比较Tab.2 Com parison of the sensitivity of parameters
从表2中可以看出新方法对参数的依赖性较小,随参数的变动,最优解基本保持稳定.RY,HF最优解的变化较大,显然新方法敏感性优于RY,HF.
(3)综合(1),(2),知FW与新算法都比RY,HF参数少,且对参数的敏感性较弱.以下分析FW与新算法的稳定性.由本文第2部分所列新的自适应函数的性质可知,可行解的收敛性及稳定性可观察其ρ(row)的分布,当ρ(row)达到1时表示,群体全部收敛到可行解[15].而由本文第3部分对新自适应惩罚函数的遗传算法的介绍,可知适应度代表最优解与精确解之间的比例,因此当适应度为1时,群体中的最优解为精确解.
图1、图2为实验结果图.
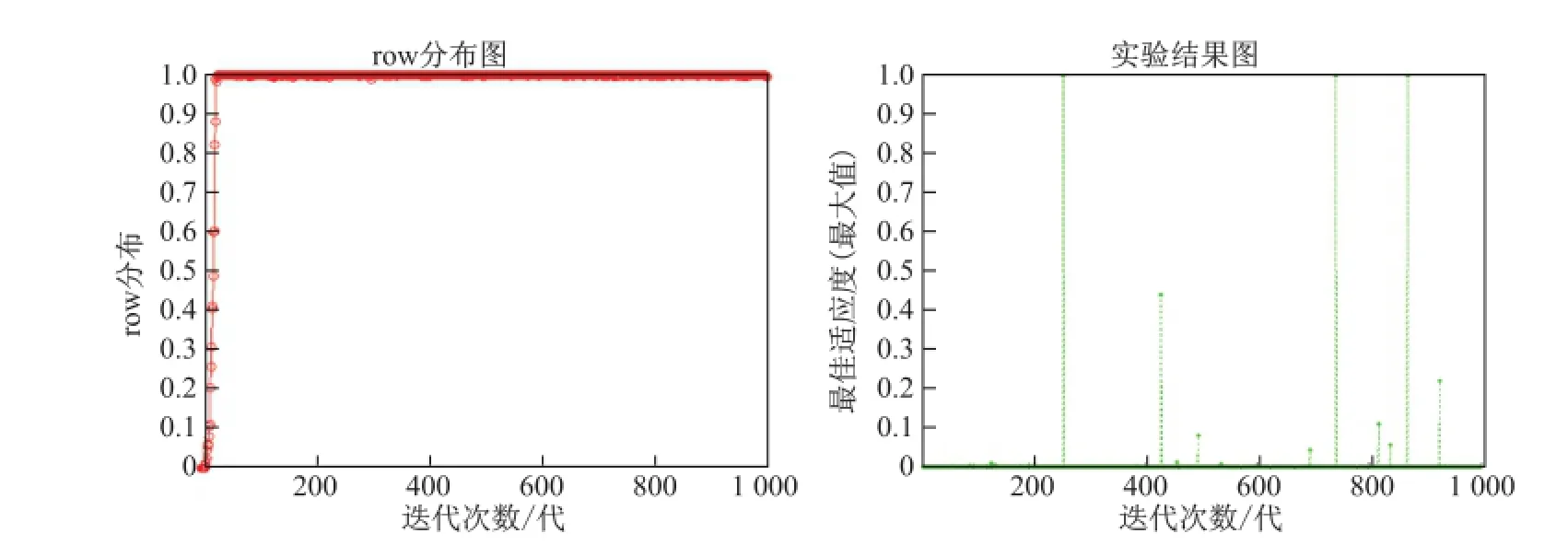
图1 新算法Fig.1 New m ethod

图2 FW算法Fig.2 FW m ethod
从实验结果上可以看出,新算法很快就全部收敛到可行域中,并且保持平稳,而Farmani和W right提出的自适应惩罚法,波动明显,证明其稳定性弱,显然新算法的收敛性以及稳定性都强于FW.
综上所述新算法对g1,g2都能得出最优解,参数较RY,HF少,且对参数的依赖性小,与Farmani和W right提出的自适应惩罚法比较,新方法的稳定性更强.新算法与RY,FW,HF相比取得了绝对优势,因此新算法有着非常大的潜力解决约束优化问题.
[1]程润伟,玄光男.遗传算法与工程优化[M].周根贵,译.北京:清华大学出版社,2004:5-13.
[2]RASH EED K.A n adap tive p en a lty ap p roach fo r constrained genetic a lgorithm op tim ization[C]//P ro ceed in gs of the 3 rd An-nu ll Genetic Programm ing Con ference.San Francisco,CA,USA:M organ,1998:584-590.
[3]甘敏,彭辉.一种新的自适应惩罚函数算法求解约束优化问题[J].信息与控制,2009,38(1):24-28.
[4]王宜举,修乃华.非线性最优化理论与方法[M].北京:科学出版社,2012:200-220.
[5]TESSEM A B,YEN G G.A self adp tive penalty function based algo rithm fo r constrained op tim ization [C]//Proceed ings o f the IEEE Congress on Evolu tionary Com pu tation.Piscataway,N J,USA:IEEE,2006: 246-253.
[6]HOUCK C R,JO INES J A.O n th e use o f non-staiona ry p ena lty fun c tion s to so lve non linear con st rained optim iza tion p rob lem s w ith GA,s[C]//P roceed ings o f the First IEEE Con feren ce on Evo lu tion ary Com pu tation. P iscataw ay,N J,U SA:IEEE,1994:579-584.
[7]闫妍.一种新的自适应遗传算法[D].哈尔滨:哈尔滨工程大学,2010.
[8]华东师范大学数学系.数学分析(上)[M].北京:高等教育出版社,2010:160-162.
[9]李广民,刘三阳.应用泛函分析原理[M].西安:西安电子科技大学出版社,2003:88-95.
[10]RUD IN W.Real and Com p lex Ana lysis(3rd Ed ition)[M].Beijing:China M achine Press,2006:103-108.
[11]HA D I-A LOUNE A B,BEA N J C.A genetic a lgorithm for the m u ltip le-cho ice in teger p rogram[J].Op erations Research,1997,45(1):92-101.
[12]RANARSSON T P,YAO X.Stochastic rank ing for constrained evolu tionary op tim ization[J].IEEE T ransactions on Evolu tionary Com pu tation,2000,4(3):284-294.
[13]FAM A N IR,W R IGHT J A.Self-adap tive fitness form u lation fo r constrained op tim ization[J].IEEE T ransa ctions on Evo lu tion ary Com pu tation,2003(7):445-455.
[14]HOM A IFAR A,Q IC X,LA I S H.Constrained op tim ization via genetic algorithm s[J].Sim u lation,1994,62(4): 242-254.
[15]COELLO A C.T heoretica l an d num erica l constraint-h and ling tech n iqu es used w ith evo lu tion ary a lgorithm s:A su rvey o f the ar t[J].Com pu ter M ethods in A pp lied M echan ics and Eng in eering,2002,191:1245-1289.
(责任编辑林磊)
A new adap tive p enalty function in the app lication of genetic algorithm
CAIHai-luan1,2,GUO Xue-ping1,2
(1.Department of Mathematics,East China Normal University,Shanghai 200241,China;2.Shanghai Key Laboratory of PMMP,East China Norm al University,Shanghai 200241,China)
Penalty function is one of the most commonly used method in genetic algorithm (GA)to solve nonlinear constraint op tim ization prob lem s.For trad itional penalty functions,it is always not easy to control penalty factors.In this paper we present a new adap tive penalty function w ith sim p ler construction and prove its convergence. Then based on this adap tive penalty function we p resent a new genetic algorithm,which can m ake populations quick ly access to feasib le regions and im p rove local search capacity of genetic algorithm s.Theoretical analysis and simu lation resu lts show that this algorithm has stronger stability and better convergence bu t needs less param eters than other ones. K ey w ord s:non linear constrained op tim ization; penalty function; genetic algorithm;adap tive penalty function
O241-43
A
10.3969/j.issn.1000-5641.2015.06.006
1000-5641(2015)06-0036-10
2014-11
国家自然科学基金(11471122,44107310);上海市科学技术委员会项目(13dz2260400)
蔡海鸾,女,硕士研究生,研究方向为数值最优化.E-mail:caihailuan@qq.com.
郭学萍,女,副教授,研究方向为数值代数、数值优化.E-mail:xpguo@math.ecnu.edu.cn.

