非线性一阶周期问题的Am b rosetti-P rod i型结果

马陆一

（西北师范大学 数学与统计学院，兰州　730070）

非线性一阶周期问题的Am b rosetti-P rod i型结果

马陆一

（西北师范大学 数学与统计学院，兰州730070）

研究了一阶周期问题解的个数与参数s（s∈R）的关系，其中a∈C（R，[0，∞）），b∈C（R，（0，∞））均为T周期函数，当u＞0时，f（u）＞0，当u≥0时，0＜l≤g（u）＜L＜∞.运用上下解方法及拓扑度理论，获得结论：存在常数s1∈R，当s＜s1时，该问题没有周期解；s=s1时，该问题至少有一个周期解；s＞s1时，该问题至少有两个周期解.

Ambrosetti-Prodi问题；上下解方法；拓扑度

0　引言及主要结果

Ambrosetti-Prodi问题是微分方程中的经典问题之一，由A.Ambrosetti和G.Prodi[1]在1972年研究二阶椭圆边值问题

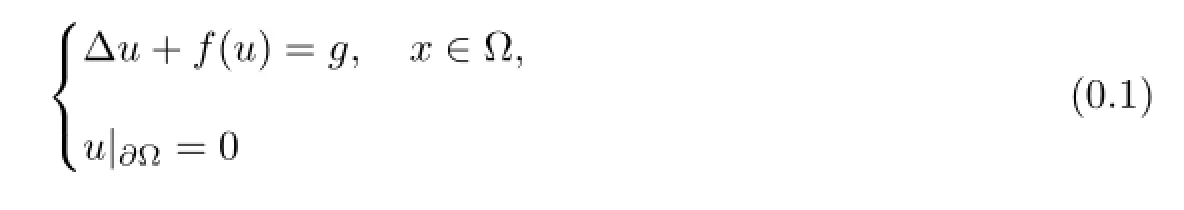
解的个数时提出，其中Ω⊂Rn是一个充分光滑的有界开集，f在u趋于±∞时线性增长，g是一个函数.他们运用拓扑度理论，获得了问题（0.1）解的存在性结果.此后这类问题受到了众多学者的关注，参见文献［2-5］.

近年来，许多学者研究了一阶周期问题解的存在性与多解性，参见文献［6-10］.特别地，Wang[6]使用锥拉伸与锥压缩不动点定理，研究了一阶带时滞微分方程

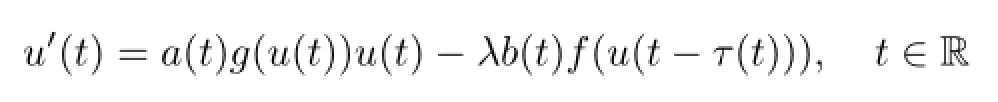
的正周期解的存在性与多解性，其中λ＞0，a，b∈C（R，［0，∞））均为T周期函数，）为T周期函数；f，g∈C（［0，∞），［0，∞）），当u＞0时，f（u）＞0，当u≥0时，0＜l≤g（u）＜L＜∞，l，L＞0.

据我们所知，对于非线性一阶周期问题，其对应的Ambrosetti-Prodi问题尚无相应的结论.本文将运用上下解方法及拓扑度理论研究一阶周期问题

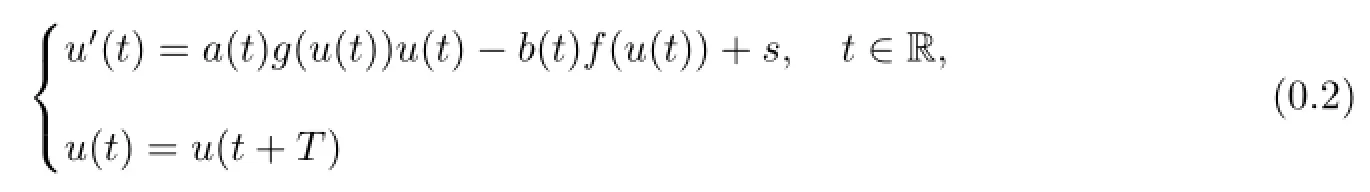
解的存在性与多解性，获得了当参数s变化时解的存在性结果，s∈R.本文假设如下条件：

（H1）a∈C（R，［0，∞）），b∈C（R，（0，∞））均为T周期函数，当u＞0时，f（u）＞0，当u≥0时，0＜l≤g（u）＜L＜∞，l、L＞0；s∈R.

本文的主要结果为：

定理0.1假设（H1），（H2）成立，则存在常数s1∈R，使得当s＜s1时，问题（0.2）无周期解；当s=s1时，问题（0.2）至少有一个周期解；当s＞s1时，问题（0.2）至少有两个周期解.

注0.2定理0.1清晰地描述了问题（0.2）解的个数与参数s的关系，而且只需要强制性条件（H2）成立.

1　预备知识

设C=C（R，R），C1=C1（R，R）.令X=｛u|u（t）∈C，u（t）=u（t+T），t∈R｝，X按范数构成Banach空间.为了方便，记

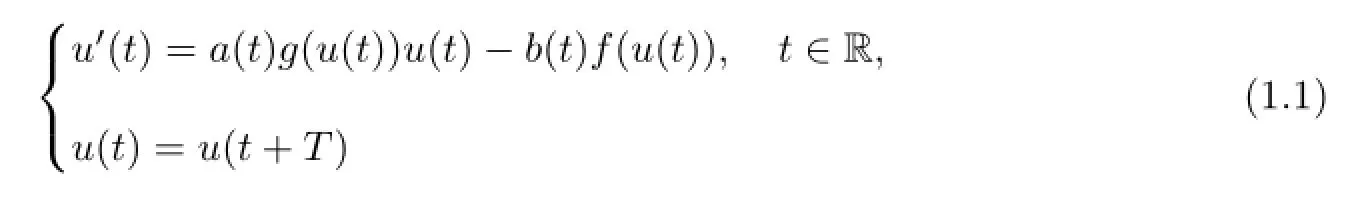
定义1.1[8]问题的一个下解α，是指α∈X∩C1，α′（t）≥ a（t）g（α（t））α（t）-b（t）f（α（t））.若α′（t）＞a（t）g（α（t））α（t）-b（t）f（α（t）），则称α为问题（1.1）的严格下解.问题（1.1）的一个上解β，是指β∈X∩C1，β′（t）≤a（t）g（β（t））β（t）-b（t）f（β（t））.若β′（t）＜a（t）g（β（t））β（t）-b（t）f（β（t）），则称β为（1.1）的严格上解.

定义算子A：X→X 为

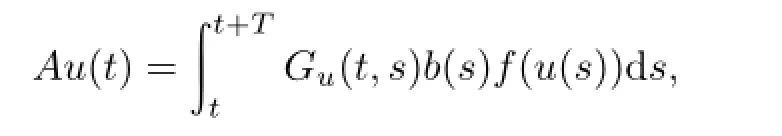
其中

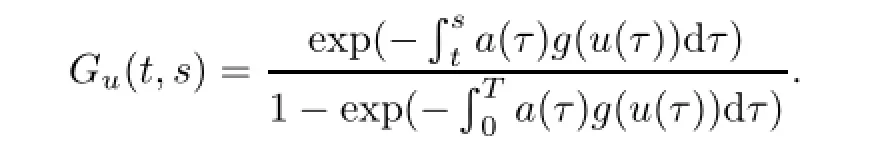
容易验证A：X→X全连续.

引理1.2[6]问题（1.1）的解u（t）等价于算子A在X上的不动点.

2　主要结果的证明

为了证明定理0.1，我们先证明下面两个引理.

引理2.1若问题（1.1）存在下解α和上解β，满足α（t）≤β（t），且当t∈R，u∈X，α（t）≤u（t）≤β（t）时，有a（t）g（u（t））≥0，a（t）g（u（t））/≡0成立.则（1.1）存在解u，满足α（t）≤u（t）≤β（t）.若β，α为（1.1）的严格上、下解，则α（t）＜u（t）＜β（t），dLS［I-A，Ωα，β，0］=1，其中Ωα，β=｛u∈X∩C1|α（t）＜u（t）＜β（t），t∈R｝.

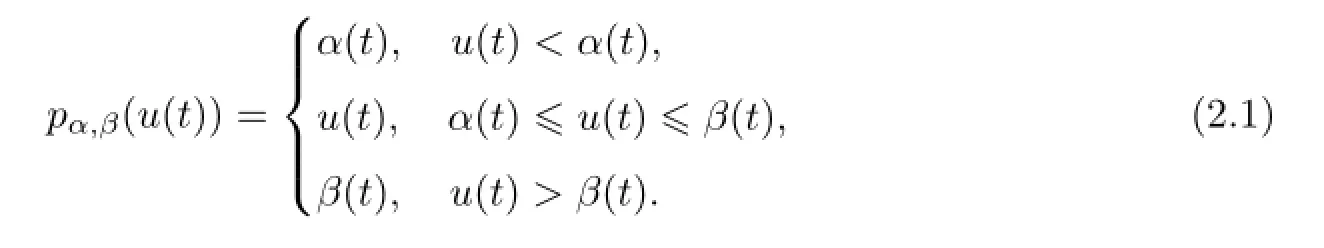
令gα，β=g（pα，β（u（t））），fα，β（u（t））=f（pα，β（u（t））），则gα，β，fα，β：X→X连续，并且gα，β（X），fα，β（X）有界.考虑辅助问题

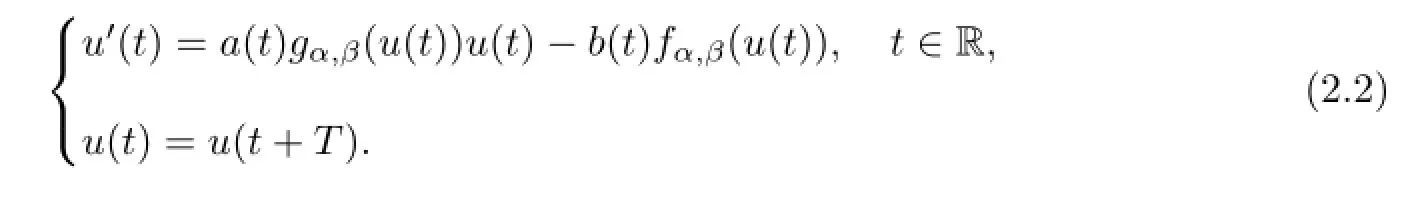
定义算子Aα，β：X→X 为

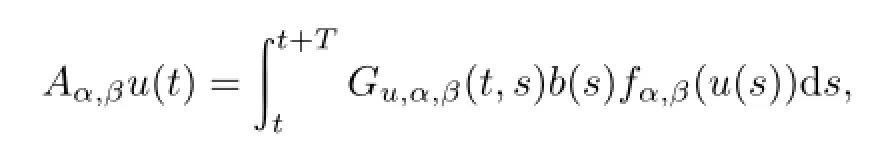
其中

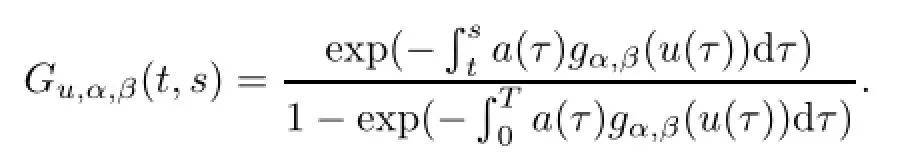
容易验证Aα，β是一个全连续算子，问题（2.2）的T周期解等价于Aα，β在X中的不动点. 由Schauder不动点定理可得，问题（2.2）有一个T周期解.

下证：如果u是辅助问题（2.2）的解，则α（t）≤u（t）≤β（t）.

假设存在t∗∈R，使得u（t∗）＞β（t∗）.不失一般性，设ω（t）=u（t）-β（t）在t∗处取得最大值.则u′（t∗）=β′（t∗）.另一方面，

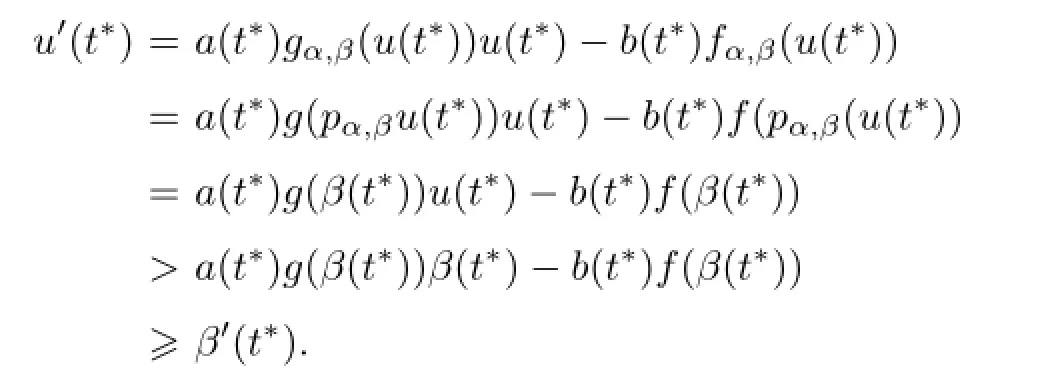
这与矛盾.因此，u（t）≤β（t），t∈R.同理可证u（t）≥α（t），t∈R.

若α，β为问题（1.1）的严格下解与严格上解.假设存在t∗∈R，使得u（t∗）≥β（t∗）.不失一般性，设ω1（t）=u（t）-β（t）在t∗处取得最大值.则u′（t∗）=β′（t∗）.另一方面，

这与矛盾.因此，u（t）＜β（t），t∈R.同理可证u（t）＞α（t），t∈R.因此辅助问题（2.2）的所有可能解u均在严格上、下解β，α之间.

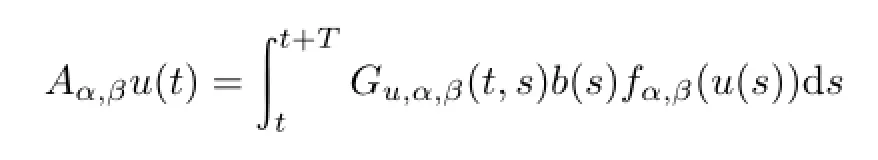
的不动点是辅助问题（2.2）的解，而（2.2）的解一定满足α（t）＜u（t）＜β（t），所以该算子在∂Ω上没有不动点.令hλ（u）=u-λAα，βu，∀λ∈［0，1］，0/∈hλ（∂Ω）.由拓扑度的同伦不变性，dLS［I-Aα，β，Ω，0］=dLS［h1，Ω，0］=dLS［h0，Ω，0］=dLS［I，Ω，0］=1.

由于辅助问题（2.2）的解均在Ωα，β中，Ωα，β⊂ Ω，结合dLS［I-Aα，β，Ω，0］=1，从而dLS［I-Aα，β，Ωα，β，0］=1.由于在Ωα，β内，问题（2.2）的等价积分算子与问题（1.1）的等价积分算子相同，所以dLS［I-A，Ωα，β，0］=1.

引理2.2 假设（H1），（H2）成立.对∀d∈R，存在ρ=ρ（d）＞0，使得对任意的s≤d，问题（0.2）的所有可能解u均属于开球Bρ中.

证明由（H1），（H2）得，∀d∈R，∃R0＞0，使得当|u|≥R0时，b（t）f（u）-a（t）g（u）u＞d.

0=u′（t0）=a（t0）g（u（t0））u（t0）-b（t0）f（u（t0））+s≤a（t0）g（u（t0））u（t0）-b（t0）f（u（t0））+d，从而b（t0）f（u（t0））-a（t0）g（u（t0））u（t0）≤d，产生矛盾.

若t0=0或T，则u′（0）≤0，u′（T）≥0，且有

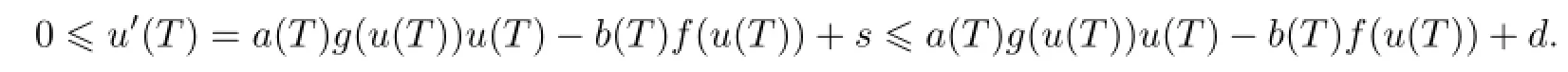
故

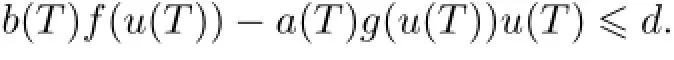
这与b（t）f（u）-a（t）g（u）u＞d矛盾.同理可证u＞-R0.

所以，问题（0.2）的所有可能的解均属于开球Bρ中.

定理0.1的证明令Sj=｛s∈R|问题（0.2）至少有j个解｝，j≥1.

（a）我们可证S1/=∅.

（c）令s1=inf S1，则|s1|＜+∞，S1⊃（s1，∞）.

令s∈R，设问题（0.2）存在解u，则

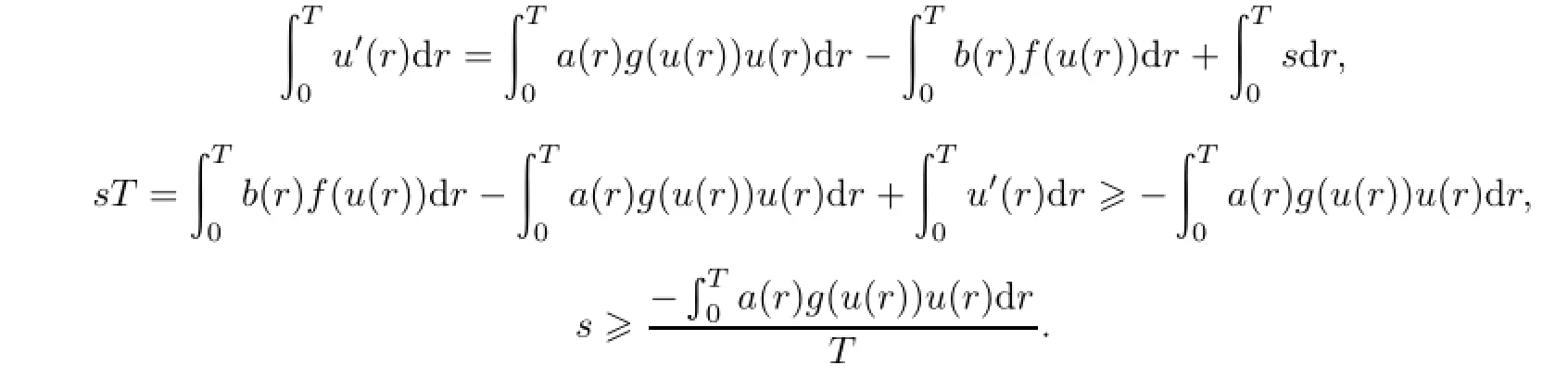
（d）S2⊃（s1，∞）.

令s3＜s1＜s2.对于任意的s∈R，令A（s，·）为问题（0.2）在X∩C1中的不动点算子.由引理2.2得，可以找到ρ，使得对于s∈［s3，s2］时，I-A（s，·）的任意可能零点u均满足u∈Bρ.因此，Leray-Schauder度dLS［I-A（s，·），Bρ，0］有定义，且不依赖于参数s.利用（c）的结论，对于u∈X∩C1，u-A（s3，·）/=0.这说明dLS［I-A（s3，·），Bρ，0］=0，结合Leray-Schauder度的同伦不变性，得dLS［I-A（s2，·），Bρ，0］=0.由Leray-Schauder度的切除性，如果则dLS［I-A（s2，·），Bρ′，0］=0.令为s∈（s1，s2）时问题（0.2）的解，则是s=s2时问题（0.2）的严格上解.取满足则R为s=s2时问题（0.2）的严格下解.由引理2.1知，当s=s2时，问题（0.2）在有一个解，且满足dL S［I-A（s2，·），0］=1.取ρ′充分大，利用Leray-Schauder度的可加性，可得

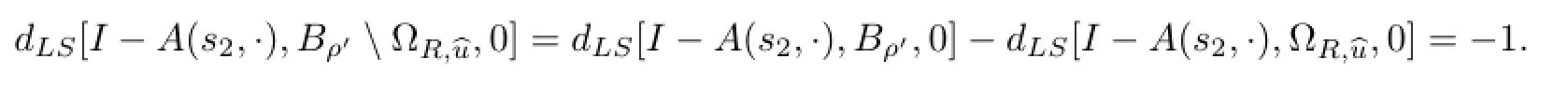
当s=s2时，问题（0.2）在中有第二个解，S2⊃（s1，∞）.

（e）s1∈S1.

令｛τk｝为（s1，+∞）中收敛到s1的一个序列，若uk为s=τk时问题（0.2）的解，则uk= A（τk，uk）.由引理2.2，对于任意的k≥1，存在ρk＞0，使得||uk||＜ρk.由A的紧性推出，uk收敛到s=s1时（0.2）的解u，s1∈S1.

因此，存在s1∈R，使得当s＜s1时，问题（0.2）无周期解；s=s1时，问题（0.2）至少有一个周期解；s＞s1时，问题（0.2）至少有两个周期解.

[1］AM BROSETT IA，PROD IG.On the inversion of som e d ifferentiab lem app ingsw ith singu larities between Banach spaces[J].A nn M a t Pu ra A pp l，1972，93:231-247.

[2］FABRY C，M AW H IN J，NK ASHAM A M N.A m u ltip licity resu lt for p eriod ic so lu toins o f forced non linear second order ord in ary d ifferenta l equ ation s[J].Bu ll London M a th So c，1986，18:173-180.

[3］RACHUNKOVA I.M u ltip licity resu lts fo r fou r-poin t boundary value p rob lem s[J].Non linear Anal，1992，18: 497-505.

[4］BEREANU C，M AW H IN J.Ex isten ce and m u ltip licity resu lts for p eriod ic so lu tions o f non linear d ifference equations[J].J D ifference Equ Ap p l，2006，12:677-695.

[5］BEREANU C，M AW H IN J.Ex isten ce and m u ltip licity resu lts fo r som e non linear p rob lem s w ith singu larφ-Lap lacian[J].J D ifferentia l Equations，2007，243（2）:536-557.

[6］WANG H Y.Positive period ic solu tions of functional d ifferential equations[J].J D ifferential Equations，2004，202:354-366.

[7］GRAEF J R，KONG L J.Ex isten ce o fm u ltip le period ic so lu tions fo r first order fun ctiona l d ifferen tia l equations [J].M a th Com pu t M odelling，2011，54:2962-2968.

[8］GRAEF J R，KONG L J.Period ic solu tions of first o rder fun ctional d ifferen tia l equations[J].A pp l M a th Lett，2011，24:1981-1985.

[9］BA ID Y，XU Y T.Period ic so lu tion s o f first order fun ctiona l d ifferentia l equations w ith period ic dev ia tions[J]. Com pu t M a th A p p l，2007，53:1361-1366.

[10］KANG S G，SH IB，WANG G Q.Existence ofm ax im a l and m inim al period ic so lu tions for first-order fun ctional d ifferen tia l equations[J].Ap p l M ath Lett，2010，23:22-25.

（责任编辑林磊）

Am b rosetti-P rod i typ e resu lts of the non linear first-order p eriod ic p rob lem

MA Lu-yi
（College of Mathematics and Statistics，Northwest Normal University，Lanzhou730070，China）

This paper shows the relationship between the parameter s and the number of solu tions of the first-order period ic p rob lemwhere a∈C（R，[0，∞）），b∈C（R，（0，∞））are T-periodic，and f（u）＞0 for u＞0，0＜l≤g（u）＜L＜∞for u≥0.By using themethod of upper and lower solutions and topological degree techniques，we p rove that there exists s1∈R，such that the p roblem has zero，at least one or at least two periodic solutionswhen s＜s1，s=s1，s＞s1，respectively.

Ambrosetti-Prodip rob lem；upper and lower solutions；topological degree

O175.8

A

10.3969/j.issn.1000-5641.2015.06.008

1000-5641（2015）06-0053-06

2014-11

国家自然科学基金（11361054）；甘肃省自然科学基金（1208RJZA258）

马陆一，男，硕士研究生.研究方向为常微分方程边值问题.E-mail：maly0318@126.com.