求解自治非线性薛定谔方程的分离变量法*

刘燕 张素英

(山西大学理论物理研究所，太原 030006)

求解自治非线性薛定谔方程的分离变量法*

刘燕 张素英†

(山西大学理论物理研究所，太原 030006)

薛定谔方程是量子力学的基本方程，与经典物理中的牛顿运动方程地位相当．本文针对哈密顿量与时间无关的量子系统，应用分离变量法研究其量子力学定态解．分别给出了包含克尔型、饱和型以及五次非线性效应的薛定谔方程的定态解，并将所得解析解与数值解进行比较．两者完全吻合．

非线性薛定谔方程， 定态解， 解析解

引言

在量子力学中，力场中微观粒子的状态用波函数来描述，决定微观粒子状态变化的方程是薛定谔方程:

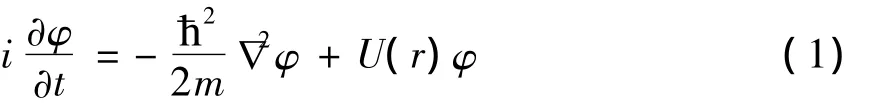
其中，－∇2+U(r)为哈密顿算符，一般情况下势能U(r)也可以是时间的函数．如果U(r)不含时间，我们可用定态微扰理论求薛定谔方程的近似解，当U(r)是时间的显函数时，我们用与时间有关的微扰理论求方程的近似解．如果U(r)与时间无关，我们也可以通过分离变量法求出方程的精确解．与频率振幅公式［1－4］、变分迭代法［5－9］、同伦分析法［10－14，21－23］、指数展开法［15－17］等求解非线性问题的方法相比，分离变量法是一种简单有效的方法．如果哈密顿量与时间无关，运用分离变量法可以快速地求出薛定谔方程的精确解．

我们考虑系统的总能量除包含动能和势能之外，还包含相互作用能，即

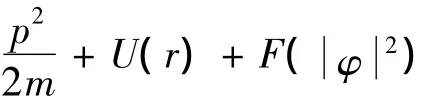
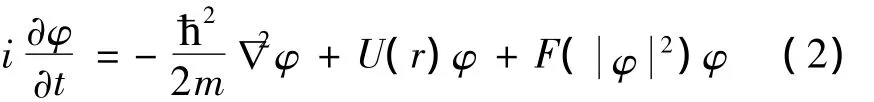
当哈密顿量与时间无关时，同样可运用分离变量法对其进行求解．本文运用分离变量法分别对包含克尔型、饱和型以及五次型非线性薛定谔方程进行求解，并将得到的结果同数值结果做比较．

1 分离变量法

如果U(r)+F()与时间无关，我们可考虑方程(2)的特解:

将方程(3)代入方程(2)中，并用u(r)v(t)去除方程两边，得到

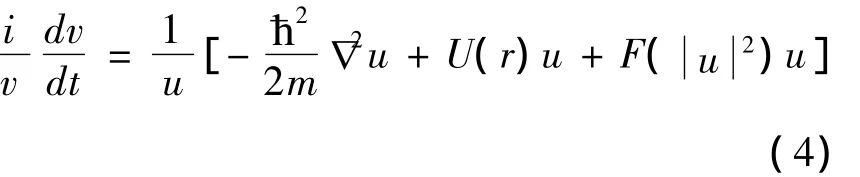
因为等式(4)的左边只是t的函数，右边只是r的函数，而t和r是相互独立的变量，所以只有当两边都等于同一常量时，等式才能被满足．以E表示这个常量，则有

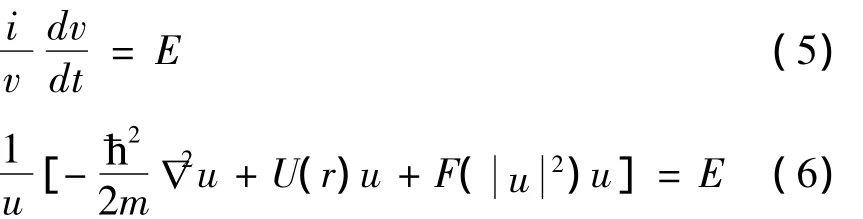
显然方程(5)的解为:

C为任意常数．从而其中，C由φ(r，0)=u(r)得到．常量E可以通过将已知的初始波函数u(r)代入方程(6)求得．根据德布罗意关系，E就是系统处于波函数φ(r，t)描述状态的能量，具有确定值，系统处于(8)式所描述的状态时，称为定态，对应的波函数φ(r，t)为定态波函数．

2 外势作用下非线性薛定谔方程的定态解

2．1 克尔型非线性薛定谔方程的定态解

我们首先考虑两维克尔型非线性薛定谔方程［18，19］:

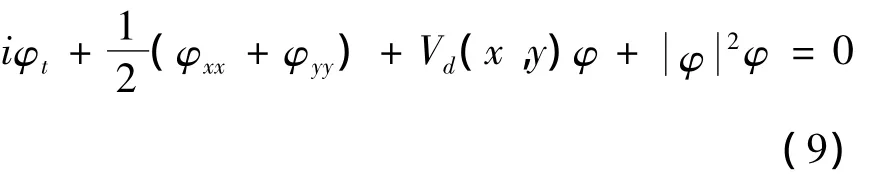
初始条件

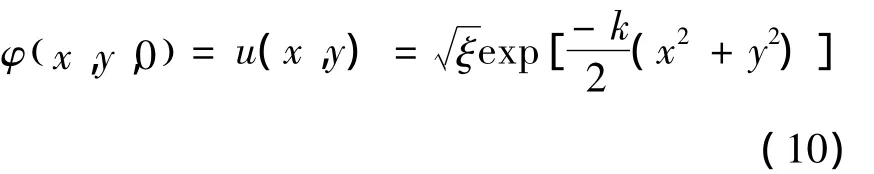
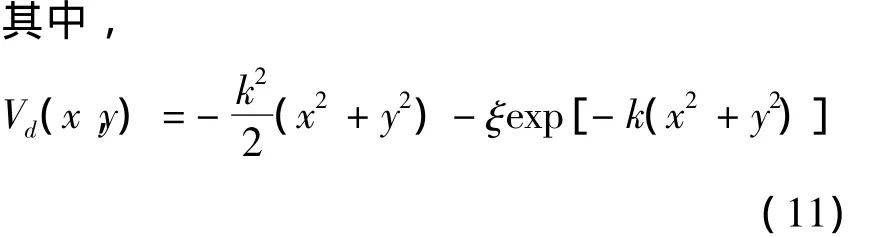
其哈密顿量与时间无关，则方程(9)存在定态解，且满足:

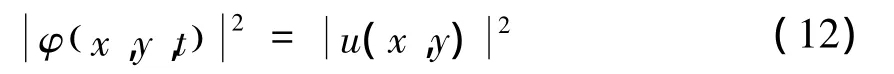
考虑方程的特解:

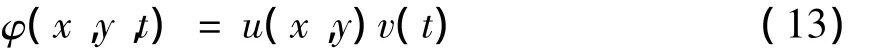
将方程(13)代入方程(9)并重新整理得

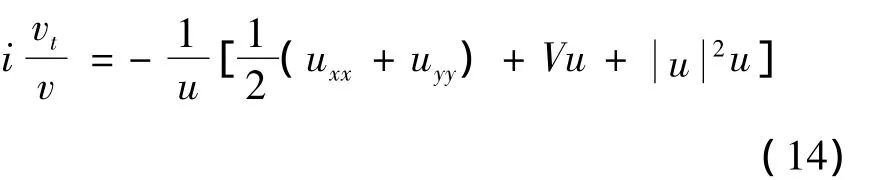
因为等式左边只是时间t的函数，右边只是x，y的函数，而t和x，y是相互独立的变量，所以只有当两边都等于同一个常量时，等式才能成立．以E表示这个常量，则有:

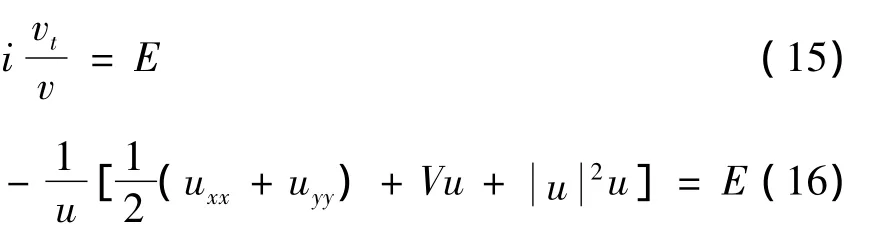
根据方程(15)得

将方程(10)代入方程(16)得E=k，角频率是个定值，系统处于定态．所以，方程(9)的定态解可表示为:

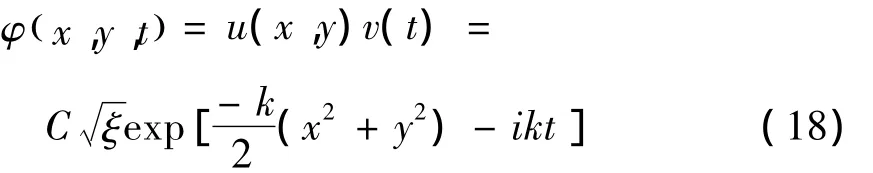
由 φ(x，y，0)=u(x，y)得C=1 ．所以方程(9)的定态解为

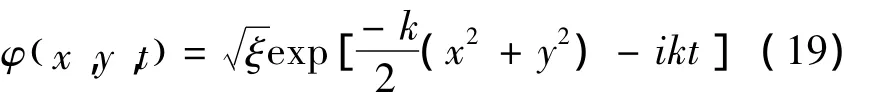
2．2 饱和型非线性薛定谔方程的定态解

偏振探测光束的传播可以用饱和型非线性薛定谔方程来描述，模型如下［19］:

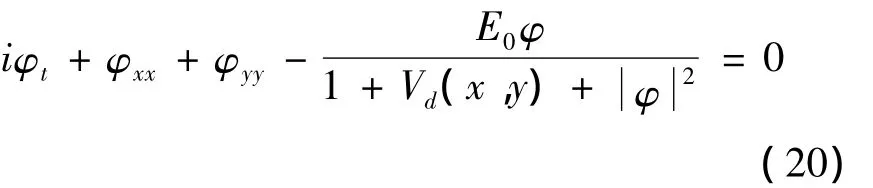
初始条件为

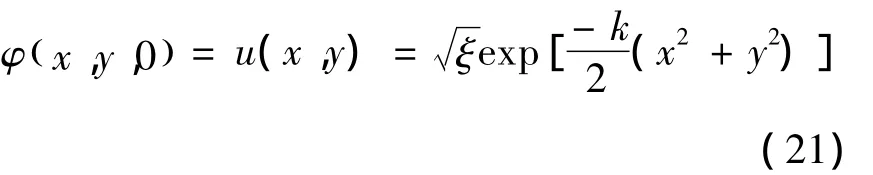
其中，φ是缓慢变化的探测光束的振幅，E0是一个常数，Vd是如下点阵密度函数:

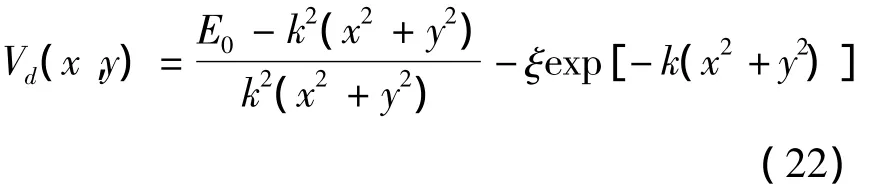
同上一小节，其定态解满足，取方程(20)的特解 φ(x，y，t)=u(x，y)v(t)，并将其代入方程(20)，重新整理得:

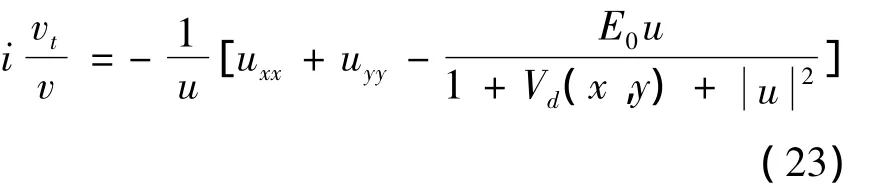
取上述等式两边等于同一个常量E得:

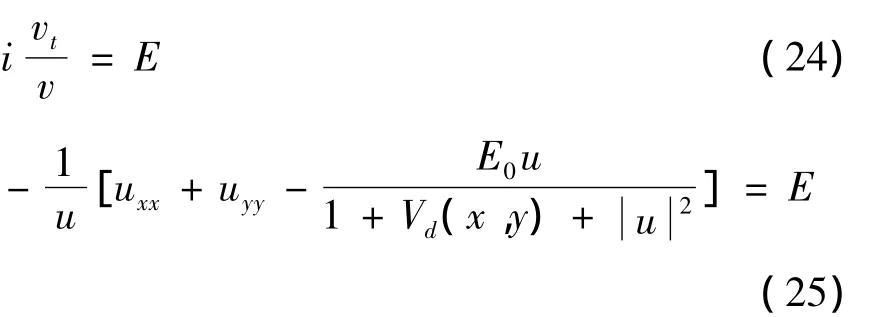
由方程(24)得v(t)=Ce－iEt．将方程(21)代入方程(25)得E=2k．所以方程(20)的定态解可表示为:

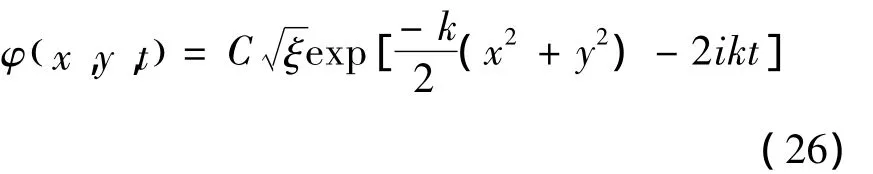
根据 φ(x，y，0)=u(x，y)，可得C=1 ．

2．3 五次型非线性薛定谔方程的定态解

五次型非线性薛定谔方程的数学模型可表示为［19］

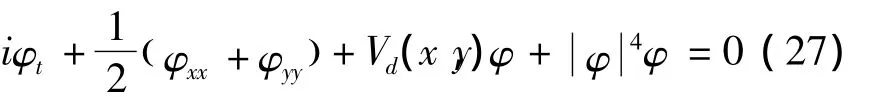
初始条件为:

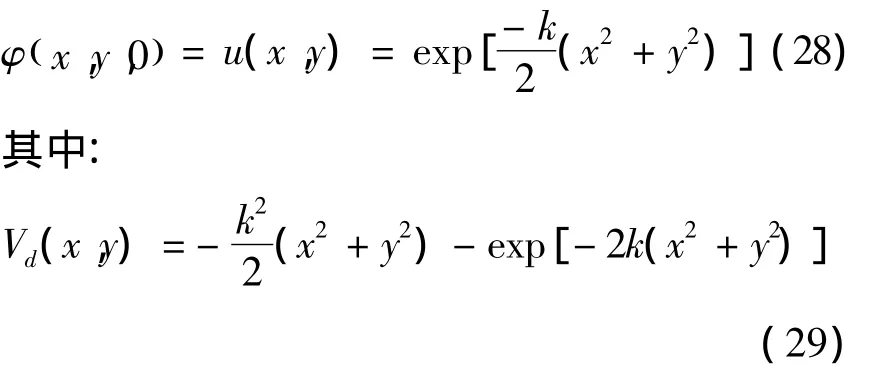
其定态解满足．取其特解 φ(x，y，t)=u(x，y)v(t)，并将其代入方程(27)，整理得:

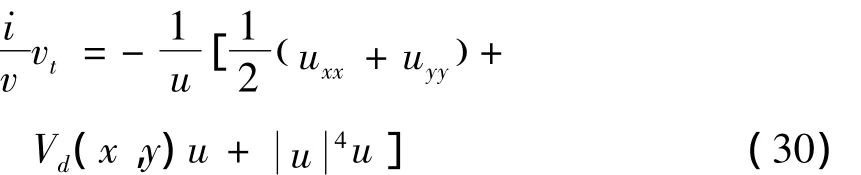
取等式两边等于同一个常量E得:

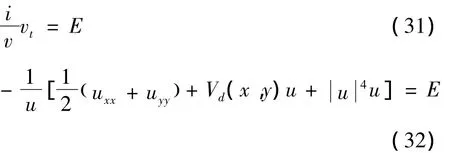
直接解方程(31)得v(t)=Ce－iEt，将(28)代入方程(32)得E=k，因此

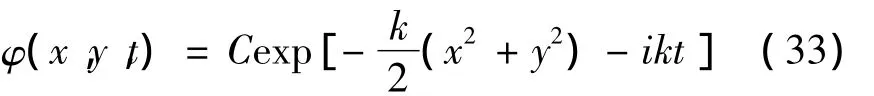
因为 φ(x，y，0)=u(x，y)，所以C=1 ．

3 解析结果与数值结果比较

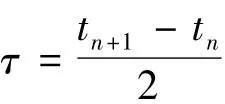
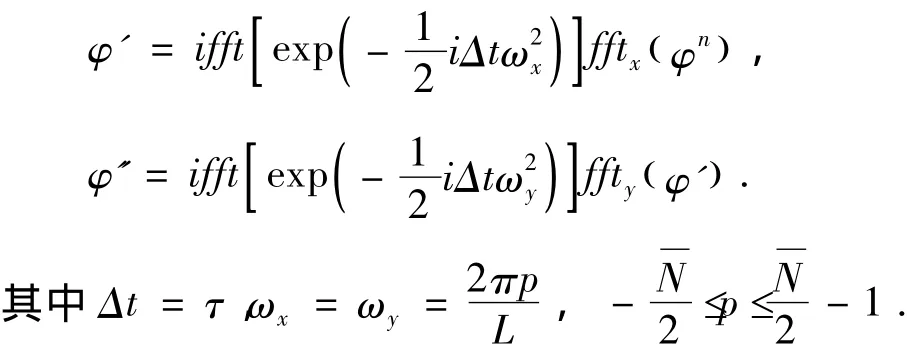
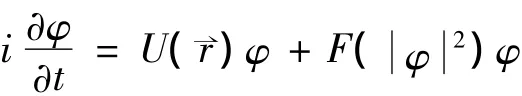
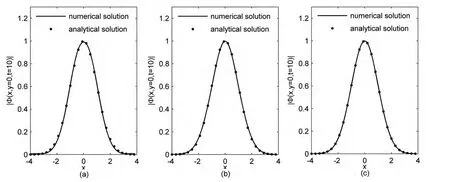
图1 非线性薛定谔方程的解析解与数值解的比较:(a)克尔非线性;(b)饱和非线性;(c)五次非线性Fig．1 Omparison between the analytical solution and the numerical solution of nonlinear Schrödinger equation(a):Kerr nonlinearity;(b)Saturable nonlinearity;(c)Quintic nonlinearity

4 结论

用分离变量法分别获得了包含克尔型、饱和型以及五次非线性效应的非线性薛定谔方程的定态解，且这三个定态解析解同数值解吻合得很好．对于哈密顿量与时间无关的薛定谔方程，分离变量法是一种特别简单而有效的方法．

1 Zhang Y N，Xu F，Deng L L．Exact solution for nonlinear Schrödinger equation by he＇s frequency formulation．Computers＆Mathematics with Applications，2009，58(11－12):2449～2451

2 He J H．An improved amplitude－frequency formulation for nonlinear oscillators．International Journal of Nonlinear Sciences and Numerical Simulation，2008，9(2):211～212

3 He J H．Comment on he＇s frequency formulation for nonlinear oscillators．European Journal of Physics，2008，29(3):L1～L4

4 Cai X C，Wu W Y．He＇s frequency formulation for the relativistic harmonic oscillator．Computers＆Mathematics with Applications，2009，58(11－12):2358 ～2359

5 Wazwaz A M．A study on linear and nonlinear Schrödinger equations by the variational iteration method．Chaos Solitons＆Fractals，2008，37(4):1136～1142

6 Zomorrodian M E，Marjaneh A M．Higher order solutions for nonlinear Schrödinger equation by hamiltonian approach．Advanced Studies in Theoretical Physics，2012，6(4):177～186

7 He J H．Variational iteration method－a kind of nonlinear analytical technique:some examples．International Journal of Non-Linear Mechanics，1999，34(4):699～708

8 He J H．Variational iteration method－some recent results and new interpretations．Journal of Computational and Applied Mathematics，2007，207(1):3～17

9 Odibat Z M，Momani S．Application of variational iteration method to nonlinear differential equations of fractional order．International Journal of Nonlinear Sciences and Numerical Simulation，2006，7(1):27～34

10 Abbasbandy S．The application of homotopy analysis method to nonlinear equations arising in heat transfer．Physics Letters A，2006，360(1):109～13

11 Liao S J．On the homotopy analysis method for nonlinear problems．Applied Mathematics and Computation，2004，147(2):499～513

12 Liao S J．Numerically solving nonlinear problems by homotopyanalysismethod．ComputationalMechanics，1997，20(6):530～40

13 He J H．Comparison of homotopy perturbation method and homotopy analysis method．Applied．Applied Mathematics and Computation，2004，156(2):527～539

14 Liang S，Jeffrey D J．Comparison of homotopy analysis method and homotopy perturbation method through an evaluation equation．Communications in Nonlinear Science＆Numerical Simulation，2009，14(12):4057～4064

15 Shou D H，He J H．Application of parameter－expanding method to strongly nonlinear oscillators．International Journal of Nonlinear Sciences and Numerical Simulation，2007，8(1):113 ～116

16 Wang S Q，He J H．Nonlinear oscillator with discontinuity by parameter－expansion method．Chaos，Solitons＆Fractals，2008，35(4):688～691

17 Xu L．Application of He＇s parameter－expansion method to an oscillation of a mass attached to a stretched elastic wire．Physics Letters A，2007，368(3－4):259 ～262

18 Wang Y，Hao R Y．Exact spatial soliton solution for nonlinear Schrödinger equation with a type of transverse nonperiodic modulation．Optics Communications，2009，282(19):3995～3998

19 Antar N，Pamuk N．Exact solutions of two－dimensional nonlinear Schrödinger equations with external potentials．Applied and Computational Mathematics，2013，2(6):152～158

20 Antoine X，Bao W Z，Besse C．Computational methods for the dynamics of the nonlinear Schrödinger/Gross－Pitaevskiiequations．ComputerPhysicsCommunications，2013，184(12):2621～2633

21 He J H．Homotopy perturbation technique．Computer Methods in Applied Mechanics and Engineering，1999，178(3－4):257 ～ 262

22 He J H．Homotopy perturbation method．a new nonlinear analytical technique．Applied Mathematics and Computation，2003，135(1):73～79

23 Pamuk S，Pamuk N．He’s homotopy perturbation method for continuous population models for single and interacting species．Computers＆Mathematics with Applications，2010，59(2):612～621

*The project supported by the National Natural Science Foundation of China(91430109)，the Specialized Research Fund for the Doctoral Program of Higher Education of China(20111401110004)，the Natural Science Foundation of Shanxi Province(2014011005－3)

†Corresponding author E－mail:zhangsy@sxu．edu．cn

A VARIABLE SEPARATION METHOD FOR SOLVING AUTONOMOUS NONLINEAR SCHRÖDINGER EQUATIONS*

Liu Yan Zhang Suying†
(Institute of Theoretical Physics，Shanxi University，Taiyuan030006，China)

The Schrödinger equations is a basic equation of quantum mechanics．It’s just as important as Newton’s equation of motion of classical physics in quantum mechanics．In this paper，we use variable separation method to obtain the stationary solution of the quantum mechanical system with time independent Hamiltonian．We separately give solutions of Schrödinger equations with Kerr type，saturation type and quintic nonlinearity．And the obtained analytical solutions are compared with the numerical solutions．They agree well with each other．

nonlinear Schrödinger equation， stationary solution， analytical solution

13 December 2014，

15 January 2015．

10．6052/1672－6553－2015－006

2014－12－13 收到第 1 稿，2015－01－15 收到修改稿．

*国家自然科学基金资助项目(91430109)，高等学校博士学科点专项科研基金资助项目(20111401110004)及山西省自然科学基金资助项目(201401100－3)

E－mail:zhangsy@sxu．edu．cn