屈服准则和硬化模型对5052铝板回弹仿真的影响
余海燕,沈嘉怡,王 友
(同济大学 汽车学院,上海 201804)
汽车质量每减少10%可使油耗下降6%~8%,汽车轻量化对降低油耗非常关键.铝合金具有低密度、高比强度,在满足性能的前提下可比钢件质量减少60%.我国的铝资源丰富,且汽车用铝的90%都可以循环利用,因此铝合金在汽车上的推广应用是必然趋势[1].同时,由于铝合金弹性模量只有钢板的1/3,所以铝合金具有比钢板更加严重的回弹问题[2-3].回弹的准确预测及其有效控制是推广铝合金应用面临的关键问题.
从塑性力学角度,一个完整的材料模型应该包括3个方面:描述材料应力应变关系的流动方程、判断材料是否进入塑性屈服的屈服准则、定义后继屈服面变化轨迹的硬化模型[4-5].现有的流动方程可分为关联和非关联流动方程[6].关联流动理论认为,塑性势函数与屈服准则采取相同的函数.目前,在金属薄板的成形仿真中多采用关联流动方程.常用的屈服准则有包括 Hill’48[7]、Hill’79[8]在内的Hill系列以及Barlat’89[9]、Barlat’91[10-11]等系列的屈服准则.硬化模型主要分为各向同性硬化模型、随动硬化模型和混合硬化模型[12-13].不同的屈服准则和硬化模型的组合加上关联流动方程就组成了不同的材料模型[14-15].
5052铝板属于Al-Mg系铝合金,由于其具有优异的防锈、高抗疲劳强度、良好的塑性与耐腐蚀性等优点在汽车上应用越来越广泛.由于铝合金属于面心立方晶体结构,且存在严重的织构,这些使得5052铝合金的弹塑性力学行为区别于其他系列的铝合金,选择适合于5052铝合金的材料模型对提高冲压成形和回弹仿真精度尤为重要[16].因此,本文对 LS-Dyna软件中 4个材料模型MAT_122、MAT_36、MAT_125、MAT_226[17]所采用的屈服准则和硬化模型进行比较分析,并采用这4个材料模型进行U形件的回弹仿真,通过U形件的冲压成形实测回弹,分析屈服准则和硬化模型对回弹精度的影响.
1 材料模型
1.1 MAT_36模型
LS-Dyna软件中,MAT_36材料模型采用的是Barlat三参数屈服准则和Hollomon各向同性硬化模型.Barlat三参数屈服准则是由Barlat和Lian[9]在1989年提出来,故又称为Barlat’89屈服准则.该准则适合于平面应力条件下面内各向异性的材料,其屈服函数如式(1)所示:

式中:σx、σy及σxy是平面应力分量;m 为材料常数,铝合金属于面心立方晶体结构,其m值为8;参数 a、c、h 及 p 可由各向异性指数 r0、r45和 r90计算得到.
各向同性硬化理论认为,后继屈服面的尺寸在改变,而屈服面位置不变,即塑性应力只与塑性应变累积有关.Hollomon各向同性硬化模型[18]可表示为

式中:σ和εp为流动应力和塑性应变,K为材料强度系数,n为应变硬化指数.
1.2 MAT_122模型
LS-Dyna中,MAT_122材料模型采用了考虑面内各向异性的Hill’48屈服准则和Hollomon硬化模型,适用于壳单元和各向异性材料的成形仿真.Hill’48屈服准则如式(4)所示:

式中,F、G、H、L、M 和 N 等参数可由 3个方向的屈服强度和剪切强度来确定[14].
1.3 MAT_125模型
LS-Dyna软件中的MAT_125材料模型是由Hill’48屈服准则与 Yoshida-Uemori(以下简称Y-U模型)[19-20]非线性随动硬化模型结合而来,适用于壳单元和体单元分析.与各向同性硬化模型相比,随动硬化模型认为后继屈服面的位置随着塑性应变而改变.描述后继屈服面中心点的轨迹矢量就称为背应力.目前常用的随动硬化模型有Chaboche系列模型[21-23]和Y-U模型,其中YU模型由日本学者Yoshida和Uemori合作提出.Y-U模型属于双屈服面模型,该模型采用屈服面和边界面来描述金属材料的塑性屈服和后继屈服行为.边界面与屈服面一样具有随动硬化特性,边界面的存在使正向与反向应变路径产生非各向同性硬化,由此可以描述硬化迟滞与后续整体硬化现象.该模型中背应力的演变遵从:

式中:dα和dβ分别是屈服面中心和边界面中心;dθ为屈服面相对边界面的移动矢量是θ的等效塑性势,其物理意义是边界面尺寸与屈服面尺寸的差;B是边界面尺寸的初始值;Y是初始屈服应力;R是各向同性硬化模量,可由式(9)确定:

1.4 MAT_226模型
LS-Dyna中,MAT_226材料模型采用了Barlat’89屈服准则与Y-U随动硬化模型.屈服准则表达式与式(1)相同,硬化模型由式(5)~(9)确定.
2 回弹仿真和U形件回弹试验
2.1 回弹仿真
U形件模具尺寸如图1所示.仿真中需要的铝合金5052的材料参数由单向拉伸试验获得.板坯为长300 mm、宽40 mm的矩形板条,长度方向与轧制方向相同.考虑模型和边界条件的对称性,仿真采用1/2模型.板料网格尺寸为2 mm,在凹模圆角对应的部位对网格进行了细分.冲压速度为1 000 mm/s,压边力为10 kN,和试验压边力一致.为分析前述4种材料模型的回弹仿真精度,分别采用 MAT_36、MAT_122、MAT_125 和 MAT_226模型对U形件的回弹进行仿真.所有仿真均采用16号全积分单元,板厚方向7个积分点,接触类型采用双面接触模型FORMING_ONE_WAY_S_S,摩擦系数0.125.显式算法模拟冲压成形,隐式算法进行回弹仿真.仿真中采用的基本材料参数密度、弹性模量、泊松比、屈服强度均采用试验获得的数据.Y-U硬化模型参数采用参考文献中的数值:Y=80 MPa、B=140 MPa、Rsat=180 MPa、b=22 MPa、C=900[19-20].

图1 U形件冲压模具尺寸
2.2 单向拉伸试验
本文研究对象5052铝板由诺贝里斯公司生产.为获得回弹仿真所需的基本力学性能参数,对5052铝板进行了单向拉伸试验,板料厚度1.0 mm.按照ASTM E8标准准备试样尺寸,标距50 mm.采用线切割沿板料轧制方向成0°、45°和90°方向加工试样.拉伸速度为3 mm/min.
拉断后的试样如图2所示,其断口截面方向与试样的拉伸方向斜交.

图2 拉断后的单向拉伸试样
图3所示是试验测得的工程应力-应变曲线.采用数据拟合的方法得到弹性模量为70.6 GPa.由于图3所示曲线没有明显的屈服平台,取0.2%工程应变下的工程应力为屈服强度,大小为165.6 MPa.抗拉强度为215.7 MPa,平均均匀延伸率约为10%.根据标准ASTM E646求得应变硬化指数为0.12.
(2)生石灰活性可影响合成硬硅钙石纤维质量,石灰活性越高,生成的硬硅钙石纤维直径越小,体积密度也越小。当煅烧温度为1 000 ℃时,生成的生石灰与平均粒径23 μm的晶质石英粉反应,合成的硬硅钙石纤维直径约为82 nm,体积密度为70.4 kg/m3。
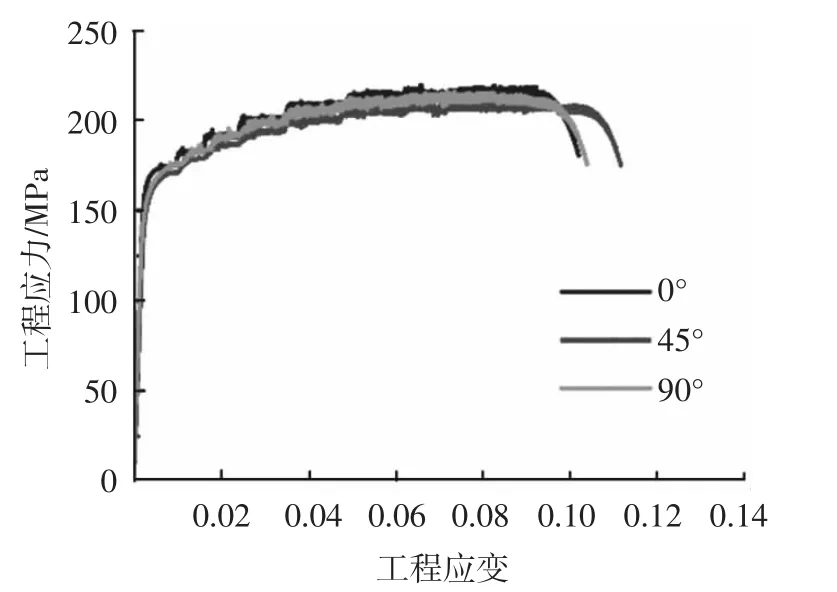
图3 5052铝合金板工程应力-应变曲线
2.3 冲压试验和回弹变形的测量
U形件冲压试验模具尺寸和毛坯尺寸与仿真完全相同.冲压行程为 45 mm,冲压速度为4 mm/s,冲压之前用润滑油对毛坯进行双面润滑,压边力为10 kN.

图4 试验U形件
图4所示为已经发生回弹的U形件,可以看到U形件的底部、侧壁和法兰部分都发生了比较明显的回弹.U形件底部产生了向外凸起,同时侧壁向内凸起形成了具有一定曲率的圆弧,法兰部分下垂.形状的回复使得侧壁和底部的夹角由直角变为钝角,法兰与侧壁的夹角变为锐角.
冲压结束后将U形件轮廓印制在白纸上,扫描获得U形件轮廓,将其导入到CAD软件中提取轮廓.然后参考 Numisheet’2011会议确定的回弹测量方法[24]在CAD软件中对U形件轮廓的回弹角和法兰的下垂量进行测量[19].如图5所示,以U形件底部中心点的水平切线为基准线,将基准线向上平移10 mm得到其和U形件轮廓的交点A,再以A点为圆心做半径为20 mm的圆弧和U形件轮廓交于B点,连接A、B两点并沿正反方向延长,AB延长线与底部基准线的夹角定义为θ1,AB延长线和法兰延长线CD的夹角定义为θ2,D点在回弹前后的高度方向的改变量为下垂量Δz.
为尽可能减少试验偶然误差的影响,试验共测量了4件,取平均值作为最终回弹试验结果.

图5 回弹测量方法示意图
3 结果分析与讨论
3.1 回弹前后Von Mises应力
U形件的冲压成形属于二维拉弯变形,主要变形区域是凹模圆角区、凸模圆角区和侧壁区.材料流经圆角区要经历弯曲-反弯曲变形,侧壁区主要是单向拉伸变形,底部与法兰区变形很小.这类变形极易使材料经受循环硬化,循环硬化下材料极易表现包辛格效应[25].另外,冲压件的回弹就是弹性卸载引起的形状回复,因此,U形件圆角区和侧壁区的等效应力在回弹前后的变化情况体现了相应材料模型在描述材料弹塑性行为准确性的一个方面.下面以MAT_125材料模型为例说明回弹前后的Von Mises等效应力变化情况,如图6所示.其他材料模型计算的等效应力变化列于表1中.

图6 MAT_125模型仿真Von Mises应力

表1 回弹前后的等效应力
由图6(a)可知,回弹前最大等效应力出现在凹模圆角区和凸模圆角区上方的区域,侧壁区域应力也比较大,这3个区域是U形件的主要变形区.在图6(b)所示的回弹后等效应力有显著下降,最大等效应力由回弹前的296.1 MPa降为回弹后的176.6 MPa.尤其是上下2个圆角部位,回弹前最大应力在这2个部位,而回弹后最大应力出现图6(b)中箭头所示的侧壁区.这说明回弹过程中圆角区的应力得到了充分释放.
如前所述,圆角区经历了弯曲-反弯曲的循环变形,也就是材料经历了拉伸到压缩再到拉伸的变形循环,多数材料在循环变形下会表现出随动硬化现象,如包辛格效应.本文所用4个材料模型中,MAT_125和MAT_226采用的是Y-U随动硬化模型,而其他2个模型采用的是各向同性硬化模型.各向同性硬化理论认为,材料在拉压状态下具有相同的塑性行为,无法描述包辛格效应,因此仿真所用材料模型是否具备描述这个现象的能力极大影响了回弹仿真精度.
3.2 回弹仿真结果分析
图7所示为采用4个材料模型仿真所得U形件轮廓.与卸载前轮廓相比,MAT_226模型预测的回弹最大,其次是MAT_125和MAT_36,MAT_122最小.
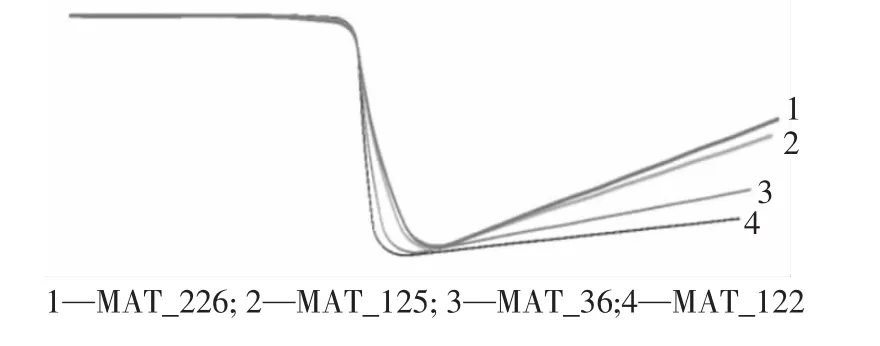
图7 U形件回弹仿真所得零件轮廓
按照2.3小节中的回弹测量方法对角θ1和θ2以及法兰的下垂量Δz进行了测量,测量结果如表2 所示.此处角度 θ1和 θ2与图 5 中含义相同,θ1和θ2与90°的差值就为相应的回弹量,Δz是回弹前与回弹后法兰端部在冲压方向z向的位移量.因此,较大的θ1和较小的θ2以及较大的Δz意味着较大的回弹.由表2可得:试验测得的θ1与θ2的回弹量分别为 12.9°和 7.2°,采用 MAT_36、MAT_122、MAT_125和MAT_226模型仿真所得θ1的回弹量分别为 7.2 °、3.9 °、10.7 °和 10.8 °,相应的 θ2的回弹量分别为 5.1 °、2.3 °、7.6 °和 7.4 °.预测结果与试验值相比有如下特点:
1)4个材料模型仿真的回弹结果均比试验值小,其中MAT_226模型预测的回弹角度与试验值最接近,MAT_125模型次之,MAT_122模型预测结果与试验值相差较大.
2)各向同性硬化模型比随动硬化模型预测的回弹小.MAT_122和MAT_36模型均建立在各向同性硬化的基础上,这2个模型预测的回弹均比基于Y-U随动硬化模型的 MAT_125模型和MAT_226模型预测结果小.
3)硬化模型相同时,Barlat’89屈服准则比Hill’48屈服准则具有更高的回弹预测精度.如MAT_36模型预测的回弹角及法兰下垂量均比MAT_122模型预测结果更接近试验值,MAT_226模型预测结果比MAT_125模型预测结果更接近试验结果.这说明对本文5052铝合金板而言,Barlat’89具有比Hill’48更高的精度.
4)硬化模型对回弹预测精度的影响程度要大于屈服准则.MAT_226与MAT_125模型均是基于Y-U随动硬化模型,而MAT_36与MAT_122模型均采用了Hollomon各向同性硬化模型.表2中MAT_226模型与MAT_125模型的回弹预测精度显著高于MAT_36和MAT_122模型.

表2 试验与仿真回弹测量结果
4 结论
1)对本文5052铝合金而言,基于Yoshida-Uemori随动硬化和Barlat’89屈服准则的材料模型预测的回弹结果与试验值最为接近;而基于各向同性硬化和Hill’48屈服准则的材料模型回弹预测精度最低.
2)随动硬化模型比各向同性硬化模型具有更高的回弹预测精度;
3)硬化模型对回弹预测精度的影响比屈服准则的影响大.
[1]KIM H S,KOC M.Numericalinvestigations on springback characteristics of aluminum sheet metal alloys in warm forming conditions[J].Journal of Materials Processing Technology,2008,204:370-383.
[2]陈超,桂枫,陈明安.铝合金板材弯曲成形性能[J].锻压技术,2013,38(1):25-30.CHEN Chao,GUI Feng,CHEN Mingan.Bending formability of aluminum alloy sheet[J].Forming &Stamping Technology,2013,38(1):25-30.
[3]王强.铝合金车身覆盖件冲压成形回弹仿真方法研究[J].农业装备与车辆工程,2012,50(4):50-54.WANG Qiang.Research of springback simulation method in aluminum alloy auto body panel stamping[J].Agricultural Equipment& Vehicle Engineering,2012,50(4):50-54.
[4]肖煜中,陈军.金属板料冲压数值模拟中的宏观硬化模型研究现状[J].塑性工程学报,2009,16(4):51-58.XIAO Yuzhong,CHEN Jun.A review of research in macroscopic hardening models in numerical simulation of sheet metal forming[J].Journal of Plasticity Engineering,2009,16(4):51-58.
[5]LEE M G,KIM C,PAVLINA E J,et al.Advances in sheet forming-materials modeling, numerical simulation and press technologies[J].J Manufacturing Sci Eng,2011,133(6):10011-10012.
[6]SAFAEI M,ZANG S L,LEE M G,et al.Evaluation of anisotropic constitutive models:mixed anisotropic hardening and non-associated flow rule approach[J].Int J Mech Sci,2013,73:53-68.
[7]HILL R.A theory of the yielding and plastic flow of anisotropic metals[J].Proceedings of the Royal Society of London.SeriesA,Mathematicaland Physical Sciences,1948,193:281-297
[8]HILL R.Constitutive modeling of orthotropic plasticity in sheet metals[J].J Mech Phys Solids,1989,38:405-417.
[9]BARLAT F,LIAN J.Plastic behavior and stretchability of sheet metals.Part I:a yield function for orthotropic sheet under plane stress condition[J].Internation-al Journal of Plasticity,1989,5:51-66.
[10]BARLAT F,LEGE D J,BREM J C.A six-component yield function for anisotropic materials[J].International Journal of Plasticity,1991,7:693-712.
[11]BARLAT F,BREM J C,YOON J W,et al.Plane stress yield function for aluminum alloy sheets-Part 1:theory[J].International Journal of Plasticity,2003,19:1-23.
[12]CAO J,LEE W,CHENG H S,et al.Experimental and numerical investigation of combined isotropickinematic hardening behavior of sheet metals[J].International Journal of Plasticity,2009,25:942-972.
[13]NOBUTADA O,WANG J D.On modeling of kinematic hardeningforratcheting behavior [J].Nuclear Engineering and Design,1995,153:205-212.
[14]EGGERTSEN P A,MATTIASSON K.On constitutive modeling for springback analysis[J].Int J Mech Sci,2010,52:804-818.
[15]WAGONER R H,LIM H,LEE M G.Advanced issues in springback [J].Int J Plast,2013,45:3-20.
[16]ZHU Y X,LIU Y L,YANG H,et al.Development and application of the material constitutive model in springback prediction of cold-bending[J].Materials& Design,2012,42:245-258.
[17]Hallquist J O.LS-DYNA keyword user's manual[M].California:Livermore Software Technology Corporation,2007,970.
[18]GRONOSTAJSKI Z.Theconstitutiveequationsfor FEM analysis[J].Journal of Materials Processing Technology,2000,106:40-44.
[19]YOSHIDA F,UEMORI T.A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation[J].International Journal of Plasticity,2002,18:661-686.
[20]YOSHIDA F,UEMORI T.A model of large-strain cyclic plasticity and its application to springback simulation [J].Int J Mech Sci,2003,45:1687-1702.
[21]CHABOCHE J L.Thermodynamic formulation of constitutive equations and application to the viscoplasticity and viscoelasticity of metals and polymers[J].Int J Solids and Structures,1997,34(18),2239-2254.
[22]CHABOCHE J L.A review of some plasticity and viscoplasticity constitutive theories[J].International Journal of Plasticity,2008,24(10):1642-1693.
[23]CHABOCHE J L,GAUBERT A,KANOUT?P,et al.Viscoplastic constitutive equations of combustion chamber materials including cyclic hardening and dynamic strain aging [J].International Journal of Plasticity,2013,46:1-22.
[24]CHUNG K,KUWABARA T,VERMA R,etal.Numisheet 2011 Benchmark 4:Pre-strain effect on spring-back of 2D draw bending[C]//The 8th International Conference and Workshop on Numerical Simulation of 3D sheet metal forming processes.New York:AIP Publishing,2011:171-175.
[25]庄京彪,刘迪辉,李光耀.基于包辛格效应的回弹仿真分析[J].机械工程学报,2013,49(22):84-90.ZHUANG Jingbiao,LIU Dihui,LI Guangyao.Analysis of springback simulation based on bauschinger effect[J].Jounal of Mechanical Engineering,2013,49(22):84-90.

