关于不定方程x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)

帅亚军，罗明(西南大学数学与统计学院，重庆400715)

关于不定方程x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)

帅亚军，罗明
(西南大学数学与统计学院，重庆400715)

运用递推数列的方法，证明了不定方程x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)无正整数解.

不定方程;整数解;递归数列

当(m，n)=1，m，n∈N*时，对形如mx(x+1)(x+2)(x+3)=ny(y+1)(y+2)(y+3)的不定方程已有不少研究工作［1-8］.1971年，Cohn［1］证明了当(m，n)=(1，2)时，不定方程仅有正整数解(x，y)=(5，4);1975年，Ponnudurait［2］证明了当(m，n)=(1，3)时，不定方程仅有正整数解(x，y)=(3，2)，(7，5);1982年，宣体佐［3］证明了当(m，n)=(1，5)时，不定方程仅有正整数解(x，y)=(2，1);1991年，罗明［4］证明了当(m，n)=(1，7)时，不定方程仅有正整数解(x，y)=(4，2);2001年，罗明［5］证明了当(m，n)=(1，6)时，不定方程仅有正整数解(x，y)=(7，4);2007年，程瑶、马玉林［6］证明了(m，n)=(1，11)时，不定方程无正整数解;2013年，郭凤明、罗明［7］证明了当n=10时，不定方程无正整数解.为此，在上述基础上利用同余式和递归数列方法证明，当m=1，n=26时，不定方程

无正整数解.

先将方程(1)化为

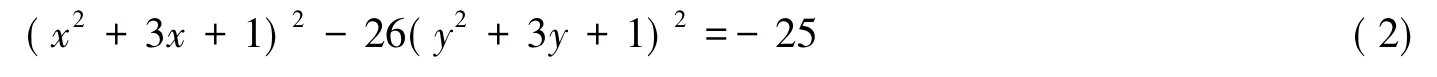
易知方程X2－26Y2=－25的全部整数解［9］，由以下4个类给出:

或者

由式(3)(4)不难推出下列关系式:

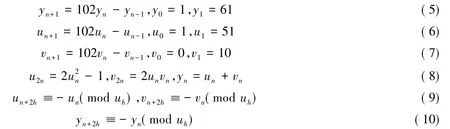
下面将证明式(3)仅当n=－1，0时成立，式(4)仅当n=0时成立.由此求得方程x2－26(y2+3y+1)2=－25的全部整数解，进一步求得式(1)的全部正整数解.

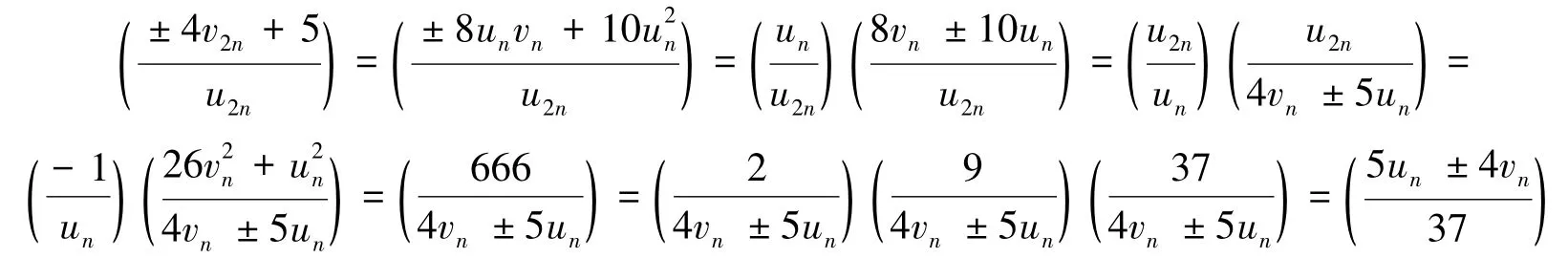
引理2若式(3)式成立，则n≡－1，0(mod 840).

证明用对序列{4yn+5}取模的方法证明.

mod 11，排除n≡1，2(mod 5)，此时4yn+5=7，7(mod 11)，剩n≡0，3，4(mod 5).

mod 191，排除n≡3(mod 5)，此时4yn+5≡112(mod 191)，剩n≡－1，0(mod 5).

mod 337，排除n≡1，3，4，5，6，7，8，9，10，13，14，，15，16，18，19，20，21，22(mod 24)，此时4yn+5≡249，288，319，72，122，77，155，68，215，131，178，98，59，28，275，270，192，279，132，216(mod 337)，剩余n≡0，－1，12，17(mod 24).

mod 3 467，排除n≡5(mod 12)，此时4yn+5≡3 308(mod 3 467)，剩n≡－1，0，12(mod 24).

下面用计算排除n≡12(mod 24).令n=24t+12，若2|t，则n≡12(mod 48)，mod 47，排除n≡12(mod 48)，此时4yn+5≡17(mod 47);若2 t，则n≡36(mod 48)，mod 47，排除n≡36(mod 48)，此时4yn+5≡40(mod 47)，故式(3)不成立.从而排除n≡12(mod 24)，剩余n≡－1，0(mod 24).因为n≡－1，0(mod 5)，n≡－1，0(mod 24)，故n≡－1，0(mod 120).

下证n≡－1，0(mod 28)，mod 197，排除n≡1，2，3，5，6，8，9，10，11，12(mod 14)，此时4yn+5≡52，67，175，26，38，155，140，32，63，181(mod 197)，剩余n≡－1，0，4，7(mod 14).

mod 6 691，排除n≡4，7，13，18，21(mod 28)，此时4yn+5≡2 034，1 618，6 532，4 667，5 083(mod 6 691).剩余n≡－1，0，14(mod 28).

下面用计算排除n≡14(mod 28)，令n=28t+14.若2|t，则n≡6(mod 8)，mod 743，排除n≡6(mod 8)，此时4yn+5≡383(mod 743);若2 t，则n≡2(mod 8)，mod 743，排除n≡2(mod 8)，此时4yn+5≡370(mod 743)，从而得证n≡－1，0(mod 28).因为n≡－1，0(mod 120)，所以n≡－1，0(mod 840).

引理3设n≡0(mod 840)且n＞0，则式(3)不成立.

1)k≡1(mod 4)时，令

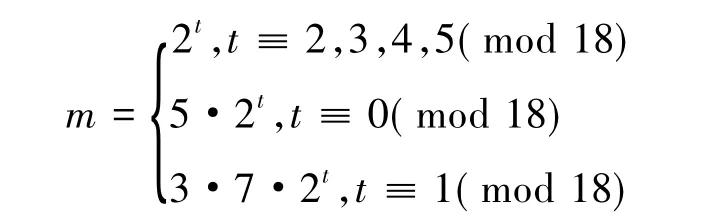
于是，由式(8)(10)及引理1，有4yn+5≡4y2m+5=4v2m+5(mod u2m)，得.从而4yn+5非平方数，故式(3)不成立.

2)k≡－1(mod 4)时，令

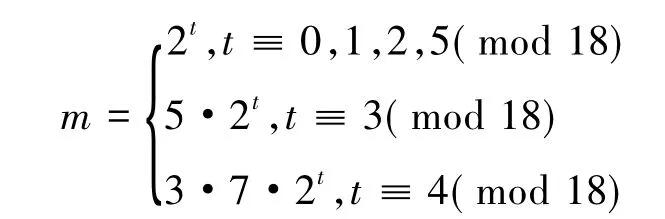
表1　k≡1(mod 4)数据情况

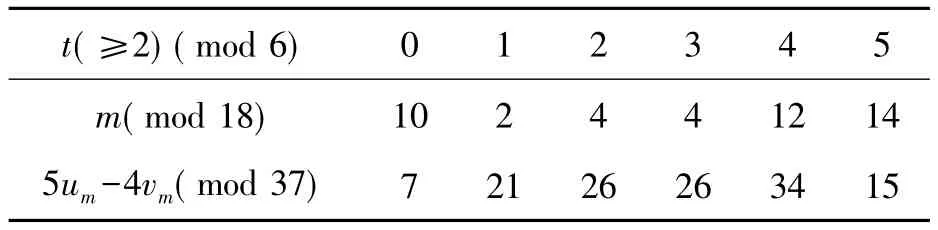
表2　k≡－1(mod 4)数据情况

于是，由式(8)(10)及引理1，有4yn+5≡－4y2m+5≡－4v2m+5(mod u2m)，得.从而4yn+5非平方数，故式(3)不成立.

证毕.

引理4设n≡－1(mod 840)且n≠－1，式(3)不成立.

当t≡0，2(mod 4)时，令m=5·2t;当t≡1，3(mod 4)时，令m=2t.则当t≡0，1，2，3(mod 4)时，m≡90， 32，80，128(mod 240)，有um≡70，159，119，192(mod 239).此时对所有的m均有

又由式(10)可得4yn+5≡－4y1+5≡－239(mod um).因2|m，则，有.从而故式(3)不成立.

证毕.

引理5若式(4)成立，则必有n=0.

证明由式(4)知(2y+3)2=－4yn+5＞0，由式(5)知，当n≠0时，yn＞1，从而，负数不可能是完全平方数.当，结论成立.

证毕.

定理1不定方程

的全部整数解是(±x，y)=(1，－1)，(1，－2)，(209，－8)，(209，5)，(1，0)，(1，－3).

证明由引理2及引理5知，要式(4)成立，则必须n=0，此时y=－1，－2.这就给出了式(11)的前两组解.

由引理3及引理5知，要式(3)成立，则必须n=－1，0，此时y=－8，5，0，－3.这就给出了式(11)的后4组解.

证毕.

推论1不定方程x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)无正整数解.

证明要让式(1)有正整数解，则由式(2)及定理1知，应有x2+3x+1=±209，但这两个方程都无正整数解.

从而方程x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)无正整数解.

证毕.

［1］COHN JE.The Diophantine Equation x(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)［J］.Pacific JMath，1971(37):240-331

［2］PONNUDURAIT.The Diophantine Equation x(x+1)(x+2)(x+3)=3y(y+1)(y+2)(y+3)［J］.JLondon Math Soc，1975(10): 232-240

［3］宣体佐.关于不定方程x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)［J］.北京师范大学学报:自然科学版，1982(2):27-34

［4］罗明.关于不定方程x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)［J］.重庆师范学苑学报:自然科学版，1991，8(1):1-8

［5］LUOM.On The Diophantine Equation x(x+1)(x+2)(x+3)=6y(y+1)(y+2)(y+3)［J］.Indian Jpure applMath，2001(1):3-7

［6］程遥，马玉林.关于不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)［J］.重庆师范大学学报:自然科学版，2007，24 (3):27-30

［7］郭凤明，罗明.关于不定方程x(x+1)(x+2)(x+3)=10y(y+1)(y+2)(y+3)［J］.西南师范大学学报:自然科学版，2013，38 (10):13-16

［8］段辉明，杨春德.关于不定方程x(x+1)(x+2)(x+3)=19y(y+1)(y+2)(y+3)［J］.四川师范大学学报:自然科学版，2009，32(1):60-63

［9］柯召，孙琦.谈谈不定方程［M］.上海:哈尔滨工业大学出版社，1980

On the Diophantine Equation x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)

SHUAIYa-jun，LUO M ing
(School of Mathematics and Statistics，Southwest University，Chongqing 400715，China)

In this paper，with themethod of recurrence sequences the author has shown that the Diophantine equation x(x+1)(x+2)(x+3)=26y(y+1)(y+2)(y+3)has no positive interger solution.

diophantine equation，interger solution，recurrence sequence

O156.2

A

1672－058X(2015)09－0053－04

10.16055/j.issn.1672－058X.2015.0009.014

2014－10－24;

2015－01－15.

帅亚军(1989-)，男，重庆巫溪人，硕士研究生，从事代数数论研究.