关于不定方程3x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)
苟莎莎(西南大学数学与统计学院,重庆400715)
关于不定方程3x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)
苟莎莎
(西南大学数学与统计学院,重庆400715)
运用递归序列和平方剩余的方法,证明了不定方程3x(x+1)(x+2)(x+3)=7y(y+1)(y+2) (y+3)仅有正整数解(x,y)=(4,3).
不定方程;整数解;递归序列;平方剩余
当(p,q)=1,p,q∈N时,形如px(x+1)(x+2)(x+3)=qy(y+1)(y+2)(y+3)的不定方程已经有不少研究工作[1-11].1971年,Cohn[1]证明了(p,q)=(1,2)时,仅有正整数解(x,y)=(5,4);1975年,Ponnudurait[2]证明了(p,q)=(1,3)时,仅有正整数解(x,y)=(3,2),(7,5);1982年,宣体佐[3]证明了(p,q)=(1,5)时,仅有正整数解(x,y)=(2,1);1982年,曹珍富[4]证明了(p,q)=(3,2)时,仅有正整数解(x,y)=(8,9);1991年,罗明[5]证明了(p,q)=(1,7)时,仅有正整数解(x,y)=(4,2);2001年,LuoMing[6]证明了(p,q)=(1,6)时,仅有正整数解(x,y)=(7,4);2007年,程瑶等[7]证明了(p,q)=(1,11)时,无正整数解;2009年,段明辉等[8]证明了(p,q)=(1,19)时,无正整数解;2009年,罗明等[9]证明了(p,q)=(3,5)时,仅有正整数解(x,y)= (7,6);2012年,瞿云云等[10]证明了(p,q)=(1,15)时,仅有正整数解(x,y)=(3,1),(25,12).但是对于p,q均大于1,且为不相连素数的情况鲜有研究.
此处将运用递归数列方法证明(p,q)=(3,7)时,不定方程

仅有一组正整数解(x,y)=(4,3).首先将方程化(1)为
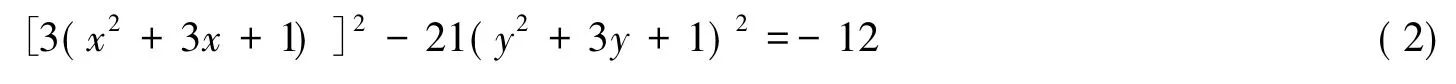
易知方程x2-21y2=-12的全部整数解由以下4个非结合类给出:
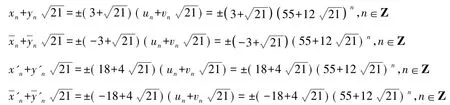
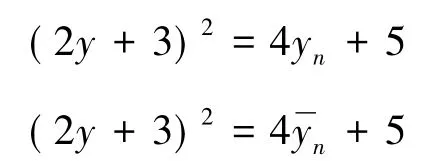

容易验证下列关系式(4)-(10)成立:

下面将分别证明式(3)当且仅当n=0,或者n=-1时成立,由此求得方程(2)的全部整数解,进而求得式(1)的全部正整数解.
1 关于(2y+3)2=4yn+5证明
本节考察n取何值时4yn+5为完全平方数.在做此工作之前先介绍几个引理.
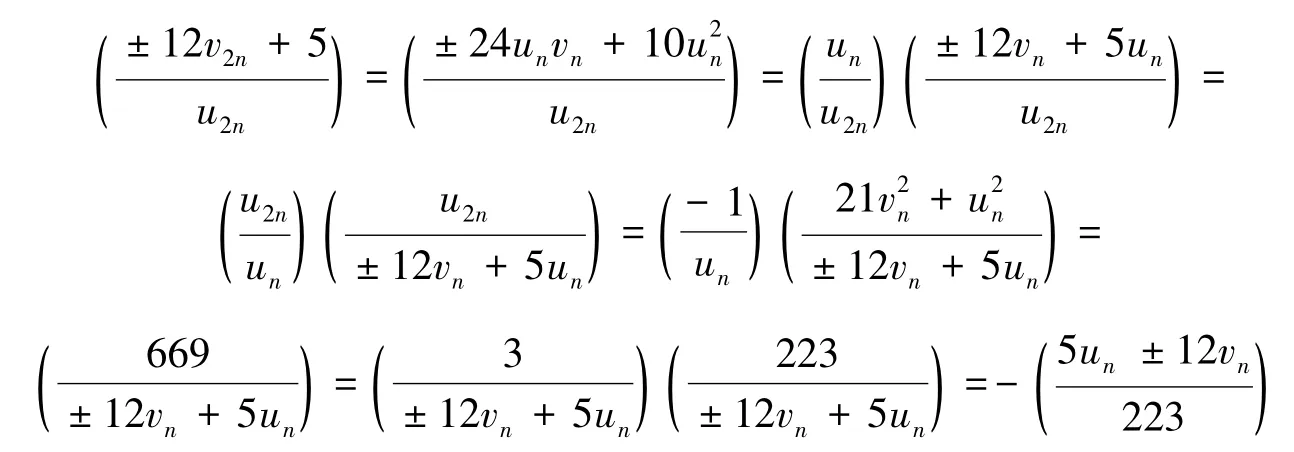
证毕.
引理2若4yn+5为平方数,则必须n≡0,-1(mod 24×32×52).
证明在此次证明中采用对序列{4yn+5}取模的方法证明.由于数字比较大,证明分3步进行.
1)先证明n≡0,-1(mod 24).
mod 17,排除n≡1,2,3,4,7,14(mod 16),此时4yn+5≡12,6,6,6,12,14,14(mod 17),剩余n≡0,5,6,8,9,10,11,12,13,15(mod 16);mod 31,排除n≡9,10,11,12(mod 16),此时4yn+5≡13,21,21,13(mod 31);mod 193,排除n≡6,8,13,15(mod 32),此时4yn+5≡122,180,180,122(mod 193);mod 1 493,排除n≡24,29 (mod 32),此时4yn+5≡1 007,1 007(mod 1 439);mod 191,排除n≡16,21,22,53,54(mod 64),此时4yn+5≡76,91,89,110,112(mod 191);剩n≡0,5,-1(mod 16),mod 263,排除n≡5(mod 8),此时4yn+5≡167(263),即n≡0,-1(mod 24).
2)再证明n≡0,-1(mod 32).
mod 53,排除n≡1,2,4,5(mod 9),此时4yn+5≡51,26,30,14(mod 53);mod 379,排除n≡6,12(mod 18),此时4yn+5≡375,10(mod 379);mod 3 511,排除n≡3,7,15,16(mod 18),此时4yn+5≡807,2 182,2 718,1 339(mod 3511);剩余n≡0,8,9,17(mod 18),即n≡0,-1(mod 32).
3)最后证明n≡0,-1(mod 52).
mod 199,排除n≡1,2,3,4,5,6,7,10,11,12,14,16,17,19,21,22,23(mod 25),此时4yn+5≡170,42,129,76,129,42,170,3,107,83,192,83,107,3(mod 199);mod 32 051,排除n≡15(mod 25),此时4yn+5≡1 749(mod 32 051);mod 421,排除n≡3(mod 5),此时4yn+5≡362(mod 421);mod 151,排除n≡9,20,34(mod 50),此时4yn+5≡133,129,28(mod 151);mod 1 619,排除n≡5,15(mod 20),此时4yn+5≡141,1 488(mod 1 619);剩余n≡0,24,49,50,74,99(mod 100),即n≡0,-1(mod 52).证毕.
引理3设n≡0(mod 24×32×52)且n>0,则4yn+5不为完全平方数.
证明令n=2×k×32×52×2t,(t≥3,2 k),对{5un±12vn}取模223,所得的两个剩余序列周期均为56,而对{2t}模56的剩余序列具有周期3.下面对k分两种情况讨论.
a)k≡1(mod 4)时,令
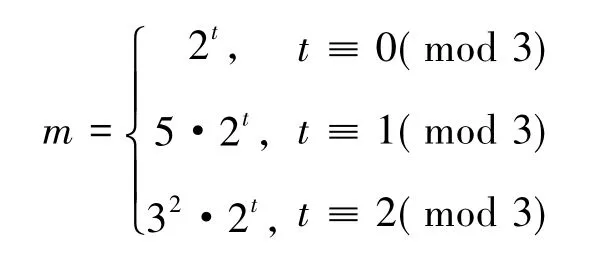
则有表1.
其中第一行表示t(t≥3)(mod 3),第二行表示m(mod 56),第三行表示5um+12vm(223).特别地,当t=1时,取m=22,此时5um+12vm≡112(mod 223);当t=2时,取m=4,此时5um+12vm≡199(mod 223).对表1中所有m,以及特殊的t=1,2时的m,均有于是由式(9)(10)及引理1,有4y+5≡4y+5≡n2m12v2m+5(mod u2m).于是得到
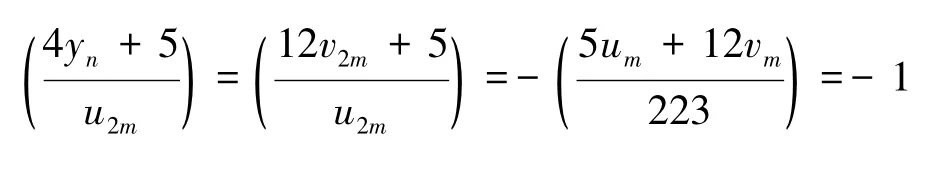
从而4yn+5是非平方数.
b)k≡-1(mod 4)时,令
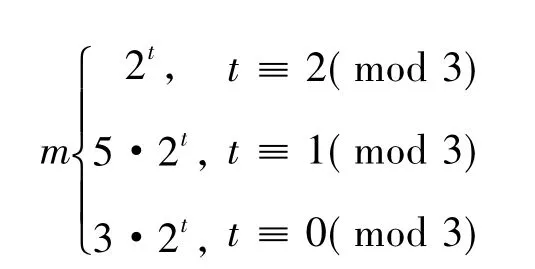
则有表2.
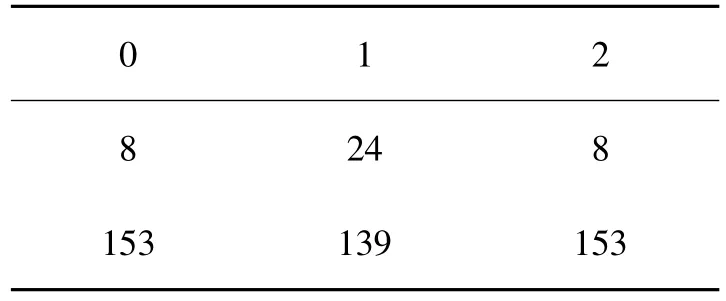
表1 k≡1(mod 4)情况下的数据
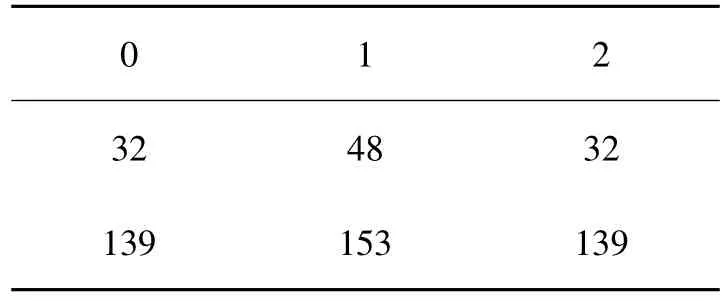
表2 k≡-1(mod 4)情况下的数据
其中第一行表示t(t≥3)(mod 3),第二行表示m(mod 56),第三行表示5um-12vm(mod 223).对表2中所有m,均有,于是由式(9)(10)及引理1,有.于是得到
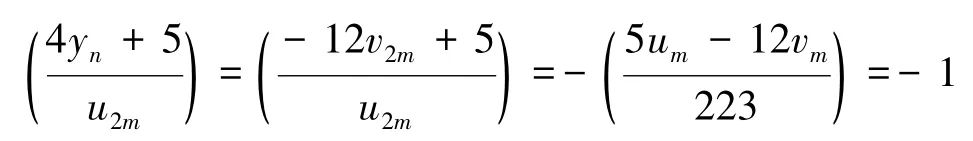
从而4yn+5是非平方数.证毕.
引理4设n≡-1(mod 24×32×52),则仅当n=-1时,4yn+5为完全平方数.
证明如果n≡-1(mod 24×32×52)且n≠-1,则可令n=-1+2·k×32×52×2t,(t≥3,2 k),由式(9)知,4yn+5≡-4y-1+5≡-71(mod um),又时,um≡1(mod 4),从而
对{um}取模71,所得的剩余序列周期为24,而对{2t}模24的剩余序列具有周期2.令
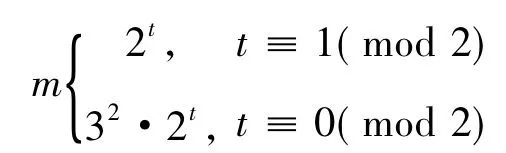
特别地,当t=1时,取m=2,此时um≡14(mod 71);当t=2时,取m=1,此时um≡61(mod 71).对所有m,包括特殊的t=1,2时的m,均有于是可知,即4y+5不为平方数,假设不成立.当n=-1n时,4yn+5=92.证毕.
3 结论
综合以上结果,现给出主要结论.
定理1不定方程3x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)仅有正整数解.
证明由引理5知
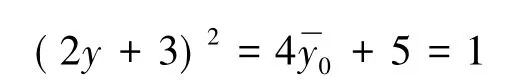
因此y=-1,-2.由引理1,2知
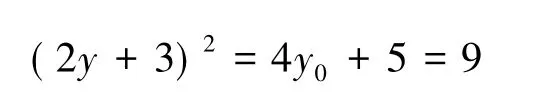
因此y=0,-3.
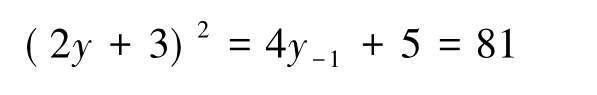
因此y=3,-6.
由此,容易知道方程(1)有16组解,其中有4组解是非平方解,它们是(4,3),(-7,3),(-7,-6),(4,-6).
因此,不定方程3x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)仅有正整数解(x,y)=(4,3).
[1]COHN JE.The Diophantine Equations x(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)[J].Pacific JMath,1971(37):311-335
[2]PONNUDUEAIT.The Diophantine Equation x(x+1)(x+2)(x+3)=3y(y+1)(y+2)(y+3)[J].JLondon Math soc,1975(10): 232-240
[3]宣体佐.关于不定方程x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)[J].北京师范大学学报:自然科学版,1982(3):27-34
[4]曹珍富.关于不定方程3x(x+1)(x+2)(x+3)=2y(y+1)(y+2)(y+3)[R].哈尔滨工业大学科研报告,1982
[5]罗明.关于不定方程x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)[J].重庆师范学院学报:自然科学版,1991,8(1):1-8
[6]LUO M.The Diophantine Equations x(x+1)(x+2)(x+3)=6y(y+1)(y+2)(y+3)[J].Indian JPure Appl Math,2001(1):3-7
[7]程瑶,马玉林.关于不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)[J].重庆师范学院学报:自然科学版,2007,24(3):27-30
[8]段辉明,杨春德.关于不定方程x(x+1)(x+2)(x+3)=19y(y+1)(y+2)(y+3)[J].四川师范大学学报:自然科学版,2009,32(1):60-63
[9]罗明,朱德辉,马芙蓉.关于不定方程3x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)[J].西南师范大学学报:自然科学版,2009,34(5):16-21
[10]瞿云云,曹慧,罗永贵,等.关于不定方程x(x+1)(x+2)(x+3)=15y(y+1)(y+2)(y+3)[J].西南师范大学学报:自然科学版,2012,37(6):9-14
[11]柯召,孙琦.谈谈不定方程[M].哈尔滨:哈尔滨工业大学出版社,1980
On the Diophantine Equation 3x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)
GOU Sha-sha
(School of Mathematics and Statistics,Southwest University,Chongqing 400715,China)
By using themethod of recurrence sequences and quadratic remainders,this paper proves that the Diophantine equation 3x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)has unique positive integer solution(x,y)= (4,3).
diophantine equation;integer solution;recurrence sequence;quadratic remainder.
O156.2
A
1672-058X(2015)09-0048-05
10.16055/j.issn.1672-058X.2015.0009.013
2014-11-01;
2015-01-10.
苟莎莎(1991-),女,四川广元人,硕士研究生,从事代数数论研究.

