关于域的扩张研究

郭宝勇(山东科技大学数学与系统科学学院，山东青岛266590)

关于域的扩张研究

郭宝勇
(山东科技大学数学与系统科学学院，山东青岛266590)

域的扩张是域的一项重要的研究内容，根据已有的域，通过扩张的方法，可以构造新的域;代数扩张能将有理数域扩充为实数域，实数域添上虚数单位i可以扩充为复数域，而有限扩张和代数扩张又有着重要联系;在有限扩张与代数扩张的基本性质的基础上，进一步探讨了实数域扩充为复数域的过程.

有限扩张;代数扩张;实数域;复数域

1　有限扩张和代数扩张

定义1［1］设域K是域F的扩域，K作为域F上线性空间的维数，称为K对F的扩张次数，记为［K: F］，若，则称K是F的有限扩张.

定义2［2］设域K是域F的扩域，若都是F上的代数元，则称K是域F的代数扩张，否则称为超越扩张.

设F(α)是域F的单扩张，当α是F上的代数元时，F(α)是F的有限扩张且［F(α):F］为α在F上极小多项式的次数;当α是F上的超越元时，F(α)是F的无限扩张.

例2令F=Q，取u=π，由于π是有理数域Q上的超越元，所以有理系数多项式且

例3实数域R添上代数元i即为复数域，即C=R(i).

定理1设域K是域F的扩域，α∈K，则下列条件等价:

(1)F(α)是域F的代数扩张;

(2)α是F上的代数元;

(3)F(α)是F的有限扩张.

证明(1)⇒(2):F(α)是F的代数扩张，而α∈F(α)，所以α是F上的代数元;

提及创新，浙江印刷集团确已迈出自己的步伐。首先，其正致力于跳出单纯的印刷加工，延长产业链，为“打造最佳综合印刷服务商”而努力。金汉宏董事长提出这样一个观点：出版社提供内容、资源，而其他部分都可交由印刷企业完成。“我们要涉及到印前的设计策划、图文制作、材料选择，印后的整体包装。出版社只需向我们提供内容，至于其他的可以依靠先进的印刷技术来实现。”其次，“机器换人”也是浙江印刷集团的增效手段之一，以推进设备自动化提升和改造工作。集团通过自动化、智能化的机器替代人工，打造一体化的生产流程，进行精细化管理，提高生产效率。

(2)⇒(3):α是F上的代数元，所以［F(α):F］为α在F上极小多项式的次数，为有限数，即［F(α):F］＜+∞，因而F(α)是F的有限扩张;

由此可以得出结论:单有限扩张⇔单代数扩张.

推论1设域K是域F的有限扩张，则K一定是F的代数扩张.

定理2［3］设E是域F的扩域，K是域E的扩域，即有FEK，则当且仅当［K:F］＜+∞时有［K:E］＜+∞，［E:F］＜+∞，而且此时［K:F］=［K:E］［E:F］.

证明设［K:F］=n＜+∞，E是F上线性空间K的子空间，所以［E:F］＜+∞.设α1，α2，…，αn是K对F的基，即α∈K，∃xi∈FE(1≤i≤n)，使也是E上线性空间K的一组生成元，故［K:E］＜+∞.

推论2若［K:F］是素数，则在K与F之间没有其他子域.

定理3［4］若E是F的代数扩张，K是E的代数扩张，则K是F的代数扩张.

证明只要证明K中每个元素都是F上的代数元即可.设α∈K，则α是E上的代数元，记g(x)=c0+c1x +…+xn是α作为E上的代数元的极小多项式，其中c0，c1，…，cn－1∈E.现作K1=F(c0，c1，…，cn－1)，Fi= F(c0，c1，…，ci)(1≤i≤n－1)，F0=F(c0)，则α是K1上的代数元.但由于c0，c1，…，cn－1都是F上的代数元，故［K－1:F］=［Fn－1:Fn－2］［Fn－2:Fn－3］…［F0:F］＜+∞，于是从F(α)K－1(α)即可推出［F(α):F］≤［K－1(α):F］=［K－1(α):K'］［K1:F］＜+∞.这就说明了α是F上的代数元.

2　数域扩张过程的理解

以实数域R扩充为复数域C的过程为例进行探讨.实数域R上的一元二次方程x2+1=0在实数域上无解，这很容易通过根的判别式进行判定(Δ＜0).所以假设这个一元二次方程的根在所要扩张到的域F中，设这个方程的根为α且有α∈F.要使F成为一个域，自然地－α也要在F中，而且实数中的四则运算在F中也要成立，很容易验证－α满足x2+1=0.实数域上的不可约多项式只有两种:一种为一次多项式，另一种为二次不可约多项式.所有的三次及其以上的实系数多项式在实数域R中是可以因式分解的.而一般的一元二次方程ax2+bx+c=0，如果它的判别式Δ＜0，则会在求根公式中出现类似于的部分，而它恰好可以通过一个实数和α表达.这样通过构造新的集合和新的四则运算可以构造出复数域C.

构造新集合C0={(a，b)|a，b∈R}，在C0中定义加法“+”和乘法“·”运算如下:

对于任意实数对(a，b)，(c，d)∈C0，令

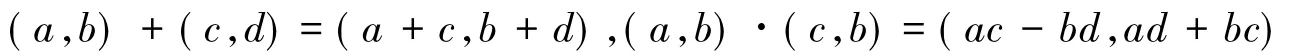
容易证明(C0，+，·)是一个域.

令C0=C1∪C2，其中由C0中其余元素组成.

这就是由实数域R扩张为复数域C的过程.

［1］姚慕生.抽象代数学［M］.上海:复旦大学出版社，2011

［2］MICHAEL ARTIN.代数［M］.北京:机械工业出版社，2009

［3］韩士安，林磊.近世代数［M］.北京:科学出版社，2009

［4］周士藩.有限域上的代数闭域的性质［J］.商丘师专学报:自然科学版，1988(2):9-10

Research on the Extension of Fields

GUO Bao-yong
(College of Mathematics and System Science，Shandong University of Science and Technology，Qingdao 266590，China)

Extension of fields is an important research content.Based on the existing fields，by themethod of extension，new fields can be constructed.The understanding of number for people is the process of the extension of number fields.Algebraic extension can expand rational number field to real number field，real number field with the imaginary unit can be extended to complex field，and finite extension and algebraic extension have important connection.Based on the basic properties of the finite extension and algebraic extension，this paper researches the process of the extension of the real number field to the complex field.

finite extension;algebraic extension;real number field;complex field

O156.2

A

1672－058X(2015)09－0031－02

10.16055/j.issn.1672－058X.2015.0009.008

2014－12－24;

2015－03－06.

郭宝勇(1989-)，男，山东泰安人，硕士研究生，从事微分方程及其应用研究.