结构参数对泵站卸荷阀影响的仿真及分析
徐 鹏
(北京天地玛珂电液控制系统有限公司,北京 100013)
0 引言
卸荷阀矿山泵站系统的关键部件之一,是实现泵站压力自动调节功能的重要压力控制元件[1],其功能是在泵持续运转的情况下满足综采工作面断续用液的需求[2],其性能的好坏对其自身可靠性以及泵站系统能否稳定运行有着直接影响[3],进而影响乳化液泵站的供液质量和系统的节能效果[4]。
本文针对某型号的泵站卸荷阀,深入分析其工作原理,建立数学模型并确定关键结构参数,利用计算机仿真技术,分析关键结构参数对卸荷阀不同性能指标的影响及其规律,并根据仿真结果优化结构设计。
1 泵站卸荷阀的工作原理
某型号的泵站卸荷阀的结构如图1所示,其主要结构分为单向阀、主阀、先导调压阀三部分,其中单向阀出口通往工作面液压系统,主阀出口通回液箱。由于矿山泵站系统工作介质为高水基乳化液,针对高水基介质易泄漏、磨损、易生锈等问题,泵站卸荷阀采用直接密封结构、耐磨材料配对等相应措施[5],先导调压阀直接选用硬度高、耐腐蚀性好的陶瓷球作为阀芯[6]。
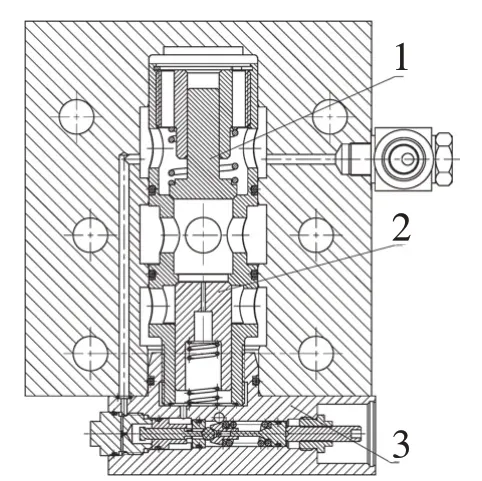
图1 泵站卸荷阀结构图
其工作原理如图2所示,泵出口液体分为四路,一路通过单向阀进入工作面液压系统,一路通过单向阀进入控制活塞腔,一路通过主阀阻尼孔以及主阀配合间隙进入弹簧腔,一路通过主阀卸荷流回液箱[2]。卸荷阀的开启由先导调压阀控制,当负载端压力大于先导调压阀设定压力时,先导调压阀开启,弹簧腔内液体流回液箱,随着先导调压阀开口量增大,流经主阀阻尼孔的压力损失增大,达到主阀开启压差,主阀开启,单向阀关闭,负载端压力通过控制活塞作用于先导调压阀维持其开启,乳化液泵通过主阀卸载。当负载端压力低于先导调压阀设定压力时,先导阀复位关闭,主阀关闭,单向阀重新开启,泵站继续向工作面供液[7]。

图2 泵站卸荷阀工作原理图
2 泵站卸荷阀的数学模型建立与分析
衡量卸荷阀性能好坏的指标为至工作面出口处的压力变化特性,即卸载阀的主阀升压与卸荷时该处允许的压力变化范围与所需时间[4],即动态特性。影响卸荷阀动态特性的因素很复杂,除阀自身结构参数之外,还受到系统中管路及其他零件影响,在本研究中忽略其他零件动态特性影响以及过液孔的液阻、阀芯自重与液压卡紧力的影响,假定阀出口压力为零,以主阀芯、先导阀芯与控制活塞为研究对象,建立如下数学模型:
1)主阀芯运动微分方程:
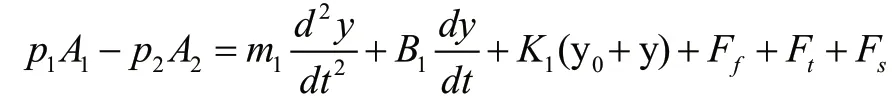
式中:Fs为作用在主阀上的稳态液动力:
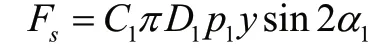
Ft为作用在主阀上的瞬态液动力:

Ff为主阀芯与阀套间的摩擦力。
2)通过主阀口的流量方程:
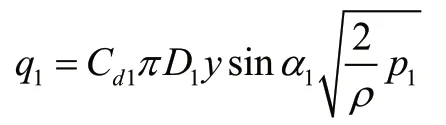
3)主阀芯阻尼孔节流方程[8]:
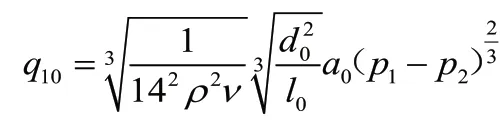
4)先导阀芯运动微分方程:

式中:Fs2为作用在先导阀上的稳态液动力:
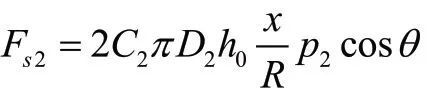
Ft2为作用在先导阀上的瞬态液动力:
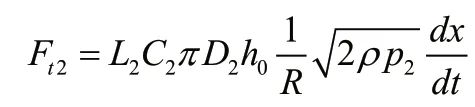
5)先导阀口流量方程:

总流量方程:

7)控制腔流量连续性方程[9]:

8)控制活塞运动微分方程:

9)先导阀开启瞬间,x=y=0,q2>0,有:
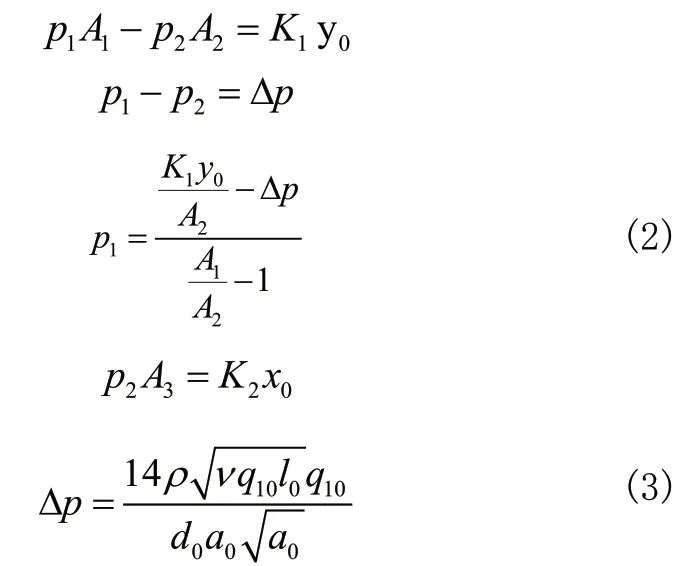
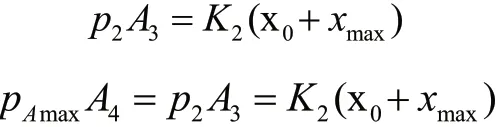
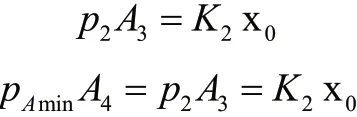
12)系统压力波动范围:
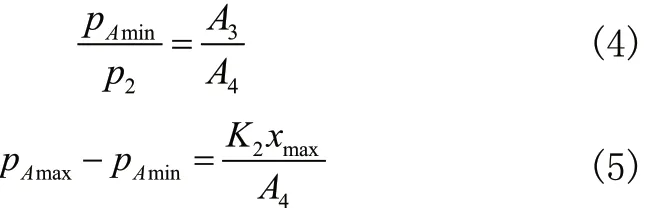
由式(1)知,压力p2的响应速度主要由主阀芯控制腔体积V0决定。
由式(2)与式(3)可知,p2由p1和pΔ决定,其关键因素的参数为K1y0、A1、A2、d0、l0值,但对p1的影响,K1y0远不如A1/A2大,对pΔ的影响,l0与d0起关键因素。
由式(4)知,系统压力下限pAmin则由先导阀口与控制活塞的面积比A3/A4和主阀芯上腔压力p2决定。
由式(5)知,先导阀调压弹簧刚度K2越大,调节灵敏度越大,x稍有变化便会导致压力波动范围增大。
综上所述,对泵站卸荷阀性能起关键作用的结构参数为阻尼孔参数l0与d0,主阀芯控制腔体积V0、先导阀口与控制活塞的面积比A3/A4、先导阀调压弹簧刚度K2和主阀芯上下腔面积比A1/A2,下面分别对其各自影响进行仿真分析。
以上公式中:
p2、p1为主阀芯上下腔的液压力(Pa);
pA为单向阀出口压力(Pa);
A2、A1为主阀芯上下腔的作用面积(m2);
A3、A4为先导阀、控制活塞作用面积(m2);
K1、K2为主阀、先导阀的弹簧刚度(N/m);
y0、x0为主阀、先导阀的弹簧预压缩量(m);
x、y、z为先导阀、主阀、控制活塞的位移(m);
m1、m2、m3为先导阀、主阀、控制活塞的质量(m);
C1、C2为主阀、先导阀阀口的流量系数;
D1、D2为主阀、先导阀出流口直径(m);
α1为主阀芯阀口半锥角;
θ为先导阀座半锥角;
R为先导球阀半径(m);
a0为阻尼孔有效作用面积(m2);
d0为阻尼孔直径(m);
l0为阻尼孔长度(m);
ρ为液体密度(kg/m3);
v为液体运动粘度(m2/s);
K为液体弹性模量(MPa);
V0为主阀芯控制腔体积(m3)。
3 Runge-Kutta算法
针对各微分方程,使用Runge-Kutta[10,11]对其进行迭代求解,该方法是一种在工程上应用广泛的求解处置问题的高精度单步算法。
假设初值问题:

该问题的解y(t)及f(t,y)足够光滑。将y(ti+1)在ti处做n阶泰勒展开,得将,得:

当h充分小时,

以上为n阶泰勒法。如果在积分区间[ti+tI+1]内,多预估几个点的斜率值,并用加权平均数作为平均斜率的近似值,经过数学推导、求解,可以得到四阶Runge-Kutta公式,也就是在工程中应用广泛的经典Runge-Kutta算法。
应用Fortran语言编写计算程序,采用Runge-Kutta算法求解描述卸荷阀模型的微分方程组,算法如图3所示,从而建立了泵站卸荷阀动态仿真分析模型,该模型能够计算泵站卸荷阀各口压力、流量和阀芯位移随时间变化规律。

图3 泵站卸荷阀动态分析算法
4 仿真结果与分析
在本研究中,我们初设单步计算时间为0.1s,计算步数为100,总计10s;计算初始变量设置为x=y=z=0mm,dx/dt=dy/dt=dz/dt=0,P1=P2=1bar。
模型主要结构参数如表1所示。

表1 模型主要结构参数
1)阻尼孔长度8mm不变,分别设定阻尼孔径为0.5mm、1mm与3mm,进行批处理运算,获得系统压力曲线如图4所示。
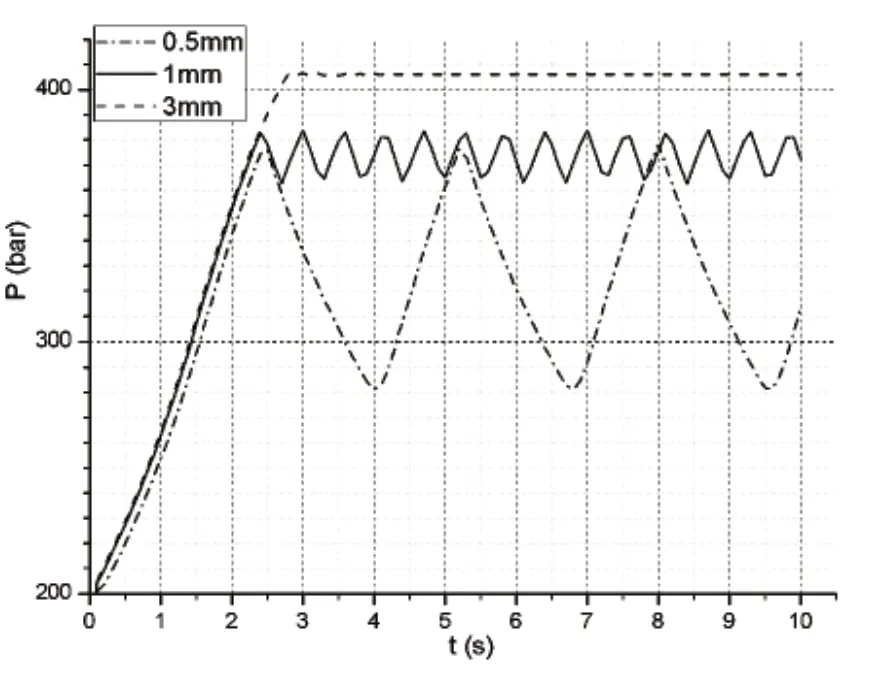
图4 不同阻尼孔径下系统压力图
由图4可看出,阻尼孔长径比越小,系统压力波动越小,响应越快,但当长径比小于某极限值时,系统压力波动为零,此时卸荷阀的工作状态为溢流,导致回液管路液体温度急剧升高,对系统不利应予避免。孔径过小,还会容易造成阻尼孔堵塞,使得卸荷阀失效。在实际设计中,应合理选取阻尼孔长径比,该参数值过大或过小均对卸荷阀性能产生不利影响。
2)主阀芯直径不变,分别设定主阀芯控制腔长度为22mm、44mm与88mm,进行批处理运算,获得系统压力曲线如图5所示。
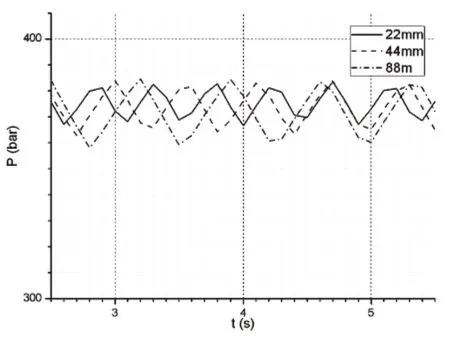
图5 不同控制腔体积下系统压力图
由图5可以看出,控制腔长度越小,即体积越小,系统压力响应越快,压力波动越小,在保证主阀芯开度满足阀口阻力损失要求的情况下,应尽量减小弹簧腔的长度,使卸荷阀获得更好的动态特性。
3)先导阀座孔直径5mm不变,分别设定控制活塞直径为5.1mm、5.3mm与6mm,进行批处理运算,获得系统压力曲线如图6所示。

图6 不同先导阀口与控制活塞面积比下系统压力图
由图6可以看出,先导阀口与控制活塞面积比越小,系统压力波动越小,响应越快,但当两者面积比接近于1时,系统压力波动为零,此时卸荷阀工作状态为溢流,应予避免。在实际设计中,应合理选取先导阀口与控制活塞面积比,该参数值过大或过小均对卸荷阀性能产生不利影响。
4)分别设定调压弹簧刚度为100N/mm、200N/mm与400N/mm,进行批处理运算,获得系统压力曲线如图7所示。
由图7可以看出,调压弹簧刚度越小,系统压力响应越快,压力波动越小,在保证调压弹簧预压缩力满足额定开启压力的情况下,应尽量减小调压弹簧刚度,从而使卸荷阀获得更好的动态特性。
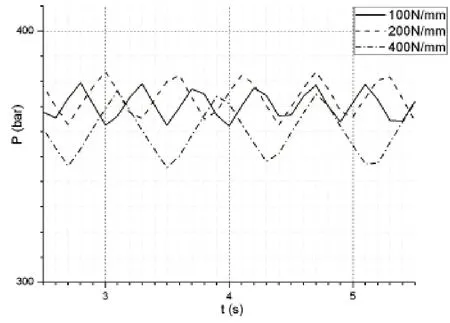
图7 不同调压弹簧刚度下系统压力图
5)主阀座孔直径(即主阀芯下腔直径)为46mm,分别设定主阀芯上腔直径为46.5mm、50mm与80mm,进行批处理运算,获得系统压力曲线如图8所示。其中主阀上腔直径80mm时阀芯位移曲线如图9所示。

图8 不同主阀上下腔面积比下系统压力图
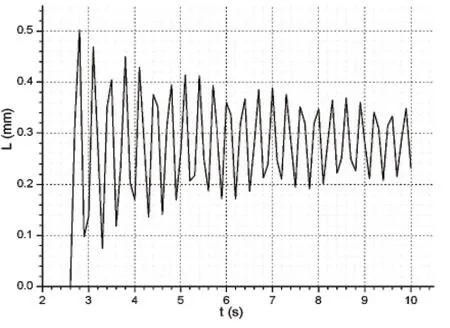
图9 上腔直径80mm时主阀芯位移图
由图8可以看出,在主阀上下腔面积比越大,系统压力波动越小,响应越快。当两者面积比超过极限值时,尽管系统压力波动在1MPa之内,但由图9可以看出,此时主阀芯在一定开度下震荡,不能实现正常开关,工作状态为溢流,应予避免。在实际设计中,应合理选取主阀芯上下腔面积比,该参数值过大或过小均对卸荷阀性能产生不利影响。
5 结束语
1)主阀芯阻尼孔长径比、主阀芯控制腔体积、先导阀口与控制活塞面积比、调压弹簧刚度、主阀芯上下腔面积比是影响泵站卸荷阀性能的5个关键结构参数。
2)减小主阀芯控制腔体积与调压弹簧刚度有利于提高泵站卸荷阀的动态响应。
3)主阀芯阻尼孔长径比、先导阀口与控制活塞面积比与主阀芯上下腔面积比的选取需适中,过大或过小均对系统不利。
4)在未来进一步的研究中,需通过试验与仿真相结合的方式对这5个参数的匹配关系进行分析,用以优化泵站卸荷阀的设计,提高产品性能。
[1] 韩建华,刘志奇.基于遗传算法的卸载阀结构参数优化[J].太原科技大学学报,2011,(08):305-308.
[2] 王国法,等.液压支架控制技术[M].北京:煤炭工业出版社,2010:19-24.
[3] 王伟.泵站溢流阀模型的动态特性仿真及分析[J].制造业自动化,2014,(08):100-102,106.
[4] 袁利才.一种新型矿用卸载阀的研究[J].液压气动与密封, 2011,(09):46-49.
[5] 弓永军,周华,杨华勇.结构参数对先导式纯水溢流阀性能的影响[J].浙江大学学报(工学版),2006,(05):869-873.
[6] 贺小峰,黄国勤,杨有胜,李壮云.球阀阀口流量特性的试验研究[J].机械工程学报,2008,(08):30-33.
[7] 李培良.电磁卸荷阀动态特性仿真及流场数值模拟[D].太原:太原理工大学,2012:11-13.
[8] 宋鸿尧,等.液压阀设计与计算[M].北京:机械工业出版社,1982:100-102,124-127.
[9] 蔡亦刚.流体传输管道动力学[M].浙江:浙江大学出版社,1990:6-8.
[10] 富明慧,梁华力.一种改进的精细龙格-库塔法[J].中山大学学报,2009,48(5):1-5.
[11] 李夏云,陈传淼.用龙格-库塔法求解非线性方程组[J].数学理论与应用,2008,28(2):62-65.

