基于多种方法分析钒与稀土对合金性能的影响*

李孟莹,张 楠,童易成,杨烨军

(1.安徽财经大学统计与应用数学学院,安徽蚌埠233030; 2.安徽财经大学金融学院,安徽蚌埠233030)

基于多种方法分析钒与稀土对合金性能的影响*

李孟莹1,张 楠2,童易成1,杨烨军1

(1.安徽财经大学统计与应用数学学院,安徽蚌埠233030; 2.安徽财经大学金融学院,安徽蚌埠233030)

针对合金性能,基于最小二乘法原理,构造拟合函数,分析单独添加微量元素钒、稀土和混合添加分别对合金抗拉强度、延伸率和热裂倾向值三方面性能的影响.利用层次分析法确定权重,运用非线性规划构造目标函数,确定单独添加微量的钒、单独添加微量的稀土以及混合添加微量的钒和稀土三种方案中使合金整体性能达到最优的方案.

合金性能;最小二乘法;钒;稀土;非线性规划

0 引言

如何进一步提高合金性能[1],各国都十分关注.合金性能的发展影响着各个产业的经济发展和国际地位,对合金性能方面的研究有很多.如孙宇等[2]基于BP神经网络模型,通过常用的力学,预测TC11钛合金的抗拉强度、屈服强度、延伸率和断面收缩率四种性能;李达人等[3]研究W Cu的添加量对合金性能的影响,并对比多种模型(体积混合物模型、German互联结构模型、Garsik微观力学模型)结果,为钨铜合金的设计提供理论依据.本文采用2014年安徽财经大学暑假数学建模模拟题A(3)的数据,基于最小二乘法、非线性规划以及层次分析法,分析单独添加钒、稀土和混合添加对合金个别性能以及综合性能的影响,最终确定合金最优综合性能下微量元素的添加方案和添加量,为合金的设计提供科学依据.

1 基于分段函数研究钒对合金性能的影响

1.1 基本假设

为了方便问题的研究,本文提出如下假设:

(1)假设实验测定出产品的抗拉强度(Mpa)、延伸率(%)和热裂倾向值(HCS)值真实有效且不存在误差.

(2)假设抗拉强度、延伸率、热裂倾向值的权重取决于其对单独添加钒与稀土数量变化的反应程度.

1.2 研究思路

1.2.1 数据分析

通过对数据进行分析发现,随着钒添加量的增加,抗拉强度、延伸率是先增后减,热裂倾向值是先减后增,且存在一个最优添加量.初步判定二次函数符合数据特征和合金化合的现实理论.由于二次函数拟合效果一般,三次函数可决系数均为1,拟合效果很好,但三次函数缺乏现实支持,所以本文综合考虑两种拟合方式,基于最小二乘法运用分段函数对问题进行研究.

1.2.2 研究方法

1.2.2.1 二次拟合函数

根据最小二乘法曲线拟合原理[4]建立二次函数,研究钒的添加量对抗拉强度、延伸率、热裂倾向值的影响,构造拟合函数:

其中:p1、p2、p3为未知参数;g1为钒的添加量;yi为抗拉强度、延伸率、热裂倾向值;ε为误差(i=1,2,3).

利用MATLAB[5]进行求解,求解出的二次拟合函数分别为:

它们的可决系数R2分别为0.815 2、0.966 6、0.852 5.求出抗拉强度、延伸率和热裂倾向值的最大值,以及相应钒的添加量:单独添加微量的钒为0.104 0时,抗拉强度达到最大值159.330 3;单独添加微量的钒为0.105 1时,延伸率达到最大值7.922 9;单独添加微量的钒为0.078 4时,热裂倾向值达到最小值91.006.

1.2.2.2 三次拟合函数

同样,依据最小二乘法建立三次函数,研究钒的添加量对抗拉强度、延伸率、热裂倾向值影响,构造拟合函数:

其中:p1、p2、p3、p4为未知参数.

利用MATLAB拟合求解,最终得出产品的抗拉强度、延伸率、热裂倾向值与钒的添加量之间的函数

关系为:

用MATLAB分别做出三次函数拟合图如图1.

图1 三次拟合曲线图Fig. 1 Cubic fitting function graphs

由图1可知,抗拉强度、延伸率、热裂倾向值的原始数据散点都出现在拟合曲线上,可决系数均为1,说明抗拉强度、延伸率、热裂倾向值与钒添加量之间的三次函数拟合效果可达到最优.但是三次函数拟合曲线最终趋向于递增或递减,对于抗拉强度与延伸率则不再存在最大值,热裂倾向值也不存在最小值,故没有相对应的最优钒的添加量(钒的添加量越多越好),这明显有悖于微合金化过程的实际情况.

1.2.2.3 分段函数

由于二次拟合函数、三次拟合函数都只是单方面考虑实际问题与精确度问题,导致二次函数回归拟合精确度不高,三次函数回归拟合缺乏现实支持,所以本文综合考虑两种拟合方式,运用分段函数原理,当钒的添加量介于0～0.2时,采用三次函数回归模型;钒的添加量大于0.2时,采用二次函数回归模型(本文以0.2为界以保证分段函数的连续性),这样分段拟合函数既符合现实又满足了高精确度.得出产品的抗拉强度、延伸率、热裂倾向值与钒的添加量之间的分段函数关系为:

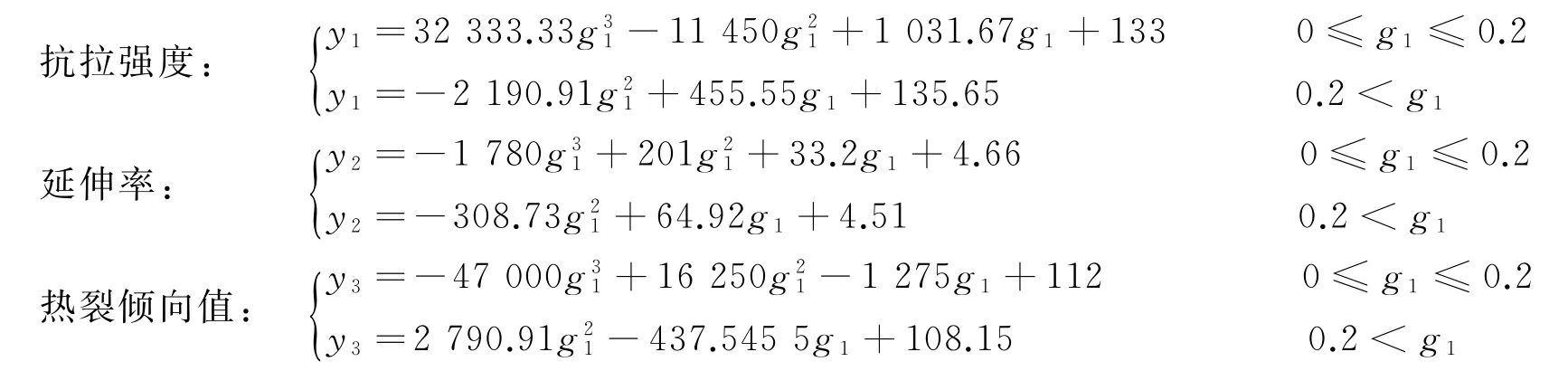
利用MATLAB做出分段函数拟合图见图2:

图2 分段函数曲线图Fig. 2 Piecew ise function graphs

由图2可知,在0～0.2的钒添加量区间内每一个散点都在拟合曲线上;抗拉强度、延伸率、热裂倾向值都存在唯一一个最优钒添加量与之对应,并且符合随着钒的添加量增加到一定程度时会影响整个合金质量的现实:随着钒的添加量增加,抗拉强度、延伸率都呈现先增后减的趋势,热裂倾向值呈现先减后增的趋势.由图2可见,函数存在两个极值点,但不影响其现实意义.求解得出:单独添加微量的钒为0.060 6时,抗拉强度达到最大值166.666 1;单独添加微量的钒为0.125 0时,延伸率达到最大值8.474 1;单独添加微量的钒为0.050 1时,热裂倾向值达到最小值82.999 8.

2 综合分析稀土对合金性能的影响

2.1 研究思路

在稀土对合金综合性能影响这一问题中,首先依旧基于最小二乘法原理,分别建立稀土与抗拉强度、延伸率、热裂倾向值的二次函数.再对这三个二次函数进行标准化处理,根据层次分析法,考虑稀土添加量对抗拉强度、延伸率、热裂倾向值的影响程度来确定权重.最后根据权重整合成一个目标函数,并对目标函数进行分析,求出最值以及所对应的稀土添加量.

2.2 研究方法

2.2.1 稀土对个别性能的影响

在研究稀土对合金不同性能的影响程度时,本文沿用上文中的二次函数模型.因为相对于其他模型而言,二次函数更加符合微合金化的实际情况,且拟合效果较好.本文利用MATLAB建立的拟合函数为:

其中:g2为稀土的添加量.

2.2.2 稀土对整体性能的影响

2.2.2.1 标准化处理

在对抗拉强度、延伸率和热裂倾向值进行综合考虑时,只有确保其类型相同,最终才能得出判断依据.

首先对三个二次函数进行标准化处理:将抗拉强度函数和延伸率函数的整体都分别除以其区间内的最大值,而热裂倾向值函数先对其整体添加负号使其转变为效益型指标,再除以其最大值,得出标准化处理后的函数分别为:

2.2.2.2 基于层次分析法确定权重

从产品的抗拉强度、延伸率和减少热裂倾向值对该合金性能重要层度的角度,通过专家打分的方法确定权重.步骤如下:

(1)建立递阶层次结构,确定层次分析的合金性能越优越好的目标层,以及建立抗拉强度、延伸率、减少热裂倾向值的准则层.由于本题只需要权重,故不计算方案的内容.层次结构见图3.

图3 层次结构图Fig. 3 Hierarchical structure

(2)构造比较判断矩阵,通过抗拉强度、延伸率、减少热裂倾向值对合金性能的重要程度两两比较,确定6个比较标准.通过查资料初步得到:延伸率对合金性能影响最大,其次为抗拉强度,再次为热裂倾向值.以此为矩阵确定的出发点,通过人为主观规定三者两两之间对比的标准值,建立矩阵如下:

(3)计算权重向量,即先将A的列向量进行归一化处理,然后将按行求和,最终将进行归一化求得权重向量为:w=(0.32,0.59,0.09).

通过对A的最大特征值及特征向量的求解,然后归一化得出抗拉强度、延伸率、减少热裂倾向值的权值.通过MATLAB求解得:判断矩阵的最大特征值λmax为3.009 2,特征向量W为(0.477 9,0.868 5,0.131 5).

(4)进行一致性检验:通过对A的最大特征值λmax及特征向量W的求解,得出矩阵一致性指标CI(CI =(λmax-n)/(n-1),其中n为A的阶数),查表得平均随机一致性指标RI=0.58,一致性比例CR= CI/RI.当CR＜0.1时,则认为判断矩阵通过一致性检验.利用M ATLAB求解得:判断矩阵的最大特征值为3.009 2;特征向量为(0.477 9,0.868 5,0.131 5);CI为0.004 6,CR=0.007 931＜0.1;A满足一致性,因而其权重向量为(0.32,0.59,0.09).

2.2.2.3 综合目标函数

利用标准化的三个函数综合为一个目标函数.本文令目标函数为:

其中:w1、w2、w3为三个函数所对应的权重;Y2为合金综合性能值.其中权重在弹性分析中已经确定,分别为0.32,0.59,0.09.最终化解目标函数为:

对该函数求导最大值解得:稀土添加量为0.132 7时,对提高产品的抗拉强度和延伸率,减少热裂倾向值在整体上有较好的影响.

3 目标规划研究钒和稀土对合金性能的影响

3.1 研究思路

本文通过二元二次函数拟合回归分别建立混合添加钒和稀土数量与抗拉强度、延伸率、热裂倾向值的函数关系式,利用STATA进行参数确定及检验,然后以热裂倾向值尽可能少为目标函数,以抗拉强度不低于150,延伸率不低于7.0等为约束条件,建立非线性规划方程模型,分析控制个别性能下钒和稀土添加量的最优添加量.

3.2 研究方法

基于最小二乘法建立二元二次函数,分析混合添加钒和稀土对抗拉强度、延伸率、热裂倾向值的影响,建立二元二次回归模型:

其中:βi为回归系数(i=0,1,2,3,4,5);ε为随机误差.

运用STATA软件进行拟合回归,求得的结果为:

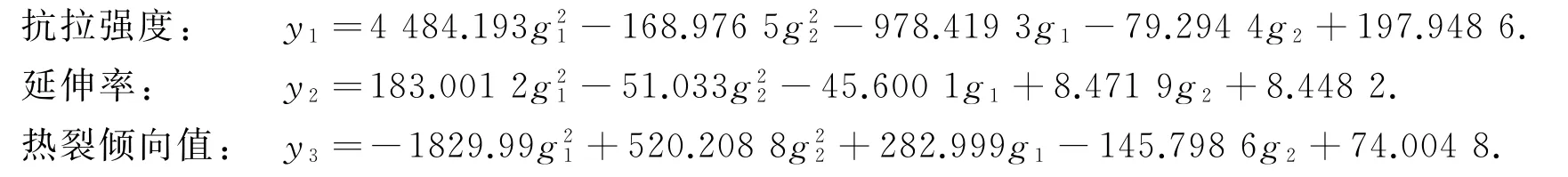
为了得出抗拉强度不低于150,延伸率不低于7.00,热裂倾向值尽可能少时,应分别添加钒和稀土的数量.本文利用非线性规划进行求解,建立热裂倾向值尽取最小的目标函数,以抗拉强度不低于150,延伸率不低于7.00为约束条件.最终建立非线性规划[6]模型为:

通过LINGO软件编程求解,得出在满足抗拉强度不低于150,延伸率不低于7.0的条件下,混合添加钒的数量为0.25.稀土的数量为0.14时,热裂倾向值达到最小值20.164 45.

4 合金最优综合性能

4.1 研究思路

确定单独添加微量的钒、单独添加微量的稀土,以及混合添加微量的钒和稀土三种方案中使合金整体性能达到最优的方案.沿用上述函数关系式和层次分析法模型中所确定的权重,将单独添加稀土所建立的分段函数、单独添加稀土建立的二次函数和混合添加钒和稀土建立的二元二次函数综合成一个目标函数,最后通过在钒和稀土数量分别在0.01～0.25的前提下对目标函数的最值进行求解比较,得出合金综合性能值最大的为最优方案.

4.2 研究结果

使用MATLAB进行求解,得出单独添加微量的钒、单独添加微量的稀土,以及混合添加微量的钒和稀土三种方案的合金综合性能值,见表1.

表1 三种方案的元素添加量与合金性能值Table 1 Element content and alloy performance value of the three kinds of scheme

从表1可以看出,混合添加钒和稀土对合金整体性能的影响最好,且微量元素的添加量比其他两种方案少,达到双优效果.

5 结论

本文综合运用最小二乘法拟合回归、非线性规划、层次分析法等方法,逐步深入研究钒和稀土对合金性能的影响,确定微量元素的添加方案和添加量.本文所建立的模型简单易懂,计算结果准确,误差小,适合广泛运用于合金的设计.

[1]袁晓光,王振玲,徐玉桥,等.铝及铝合金导电性能的研究现状及前景[C]∥中国机械工程协会.第三届中国国际压铸会议论文集:2003年卷.沈阳:东北大学出版社,2003:201-207.

[2]孙宇,曾卫东,赵永庆,等.基于BP神经网络的TC11钛合金工艺——性能模型预测[J].稀有金属材料与工程,2011, 40(11):1 9511 954.

[3]李达人,蔡一湘,刘祖岩,等.W-Cu合金物理性能模型及理论值计算[J].中国钨业,2011,26(6):35-38.

[4]李子奈,潘文卿.计量经济学[M].北京:高等教育出版社,2010.

[5]卓金武,魏永生,秦健,等.MATLAB在数学建模中的应用[M].北京:北京航空航天大学出版社,2001.

[6]杨桂元,黄已立.数学建模[M].北京:中国科学技术大学出版社,2009.

90C27,90C36

Effect of Vanadium and Rare Earth on the Properties of Alloys Based on a Variety of Methods

LI Mengying1,ZHANG Nan2,TONG Yicheng1,YANG Yejun1
(1.School of Statistics and Applied Mathematics,Anhui University of Finance and Economics,Bengbu 233030,China; 2.School of Finance,Anhui University of Finance and Economics,Bengbu 233030,China)

According to the properties of the alloy,and based on the least square method,and structure function,this paper analyzes the single addition of trace element vanadium,rare earths as well as the mixture of the two on the performance the three aspects of tensile strength,elongation and hot cracking tendency.We use the AHP to determine the weight and construct the objective function by using nonlinear programming.Finally we determine which three schemes(the single addition of trace element vanadium,rare earths and the mixture of the two)to achieve optimal overall performance of alloy.

the properties of the alloy;least square method;vanadium;rare earth;nonlinear programming

O241

A

1009-1734(2015)08-0011-06

[责任编辑 吴志慧]

2015-05-05

国家级大学生创新创业训练项目(201410378197)._

杨烨军,讲师,博士,研究方向:宏观经济统计分析.Email:21138873@qq.com

MSC 2010:90C27,90C36