模糊层次分析法在课堂教学质量评价中的应用

黄煜栋 陈兰生

摘 要：课堂教学质量评价是高校整体教学质量评价体系中的重要组成部分。考虑到传统的层次分析法在评价过程中的局限性，文章基于模糊层次分析法，建立了课堂教学质量评价指标体系，得到影响课堂教学质量的主要因素以及各类评价人员的权重，改进并优化了学生评教数据的计算方法。仿真实例表明，模糊层次分析法能提高课堂教学质量评价的客观度。相对于单因素评价法而言，其准确性更高，同时也证明了此方法有较强的可行性与有效性。

关键词：课堂教学质量；模糊层次分析法；评价

中图分类号：G712 文献标志码：A 文章编号：1673-8454（2015）14-0082-05

一、引言

随着高职教育的快速发展，教学质量问题已经成为人们密切关注的热点问题。提高教学质量是当前高职教育的重中之重，而提高课堂教学质量又是提高教学质量的核心要素。因此，课堂教学质量直接事关高职学校的生存和发展，如何对课堂教学质量进行准确、客观的评价一直以来是高职教育研究的焦点与热点问题。目前，高职课堂教学质量评价存在以下几点问题。

1.影响课堂教学质量的影响因素很多

传统的教学质量评价大多采用定性分析法，或者使用AHP（层次分析法）将定性因素转换为定量分析。这些方法在评价过程中大多都存在主观性与片面性，评价的结果不能有效反映客观的课堂教学状态，数据的准确性不高。因此，对这样的评价大部分一线教师都心存疑惑。

2.评价人员对课堂教学质量的关注点不同

对于课堂教学质量的评价一般包括企业技术人员、校内外督导、课程组成员、其他教师以及授课班级学生这五类人员，这些人员对于课堂教学质量的关注点基本没有太大的交集。企业技术人员主要关注该课程是否将技能点应用于实践，校内外督导主要关注教学设计与课堂教学安排等，而学生主要关注教师的课堂教学内容和方法是否有趣，是否能引导他们学有所成。因此这5类人员的评价所得数据所对应的权重应有所不同，但目前对这5类人员的课堂教学质量评价的权重还鲜有人开展研究并加以考虑。

3.学生评教数据的获取存在偏差

目前学生的评教一般安排在每个学期期末进行，学生通过登录学院的教务管理系统——评教模块，针对其中的各项指标进行打分，再通过一定的计算并最终获得该班级该课程授课教师的学评教分。实际中，学生的评教在分值上有较大的缺陷。因为，虽然大部分学生打分比较理性，但还是有一部分学生不够理性，是由主观意志给出评教分数的，评价结果与实际情况之间会存在不小的偏差。

针对以上几点问题，结合课堂教学质量描述本身就具有一定的不确定性（模糊性）的特点，本文在合理确定五类人员课堂教学质量评价指标的基础上，运用FAHP来确定各参评指标以及各类评价人员评价分值的权重，再对学生评教结果进行“客观化”处理，最终得到教师课堂教学质量的评价结果，并通过仿真实例验证此方法的有效性与可行性。

三、模糊层次分析法在课堂教学质量评价中的应用

1.课堂教学质量评价的层次结构

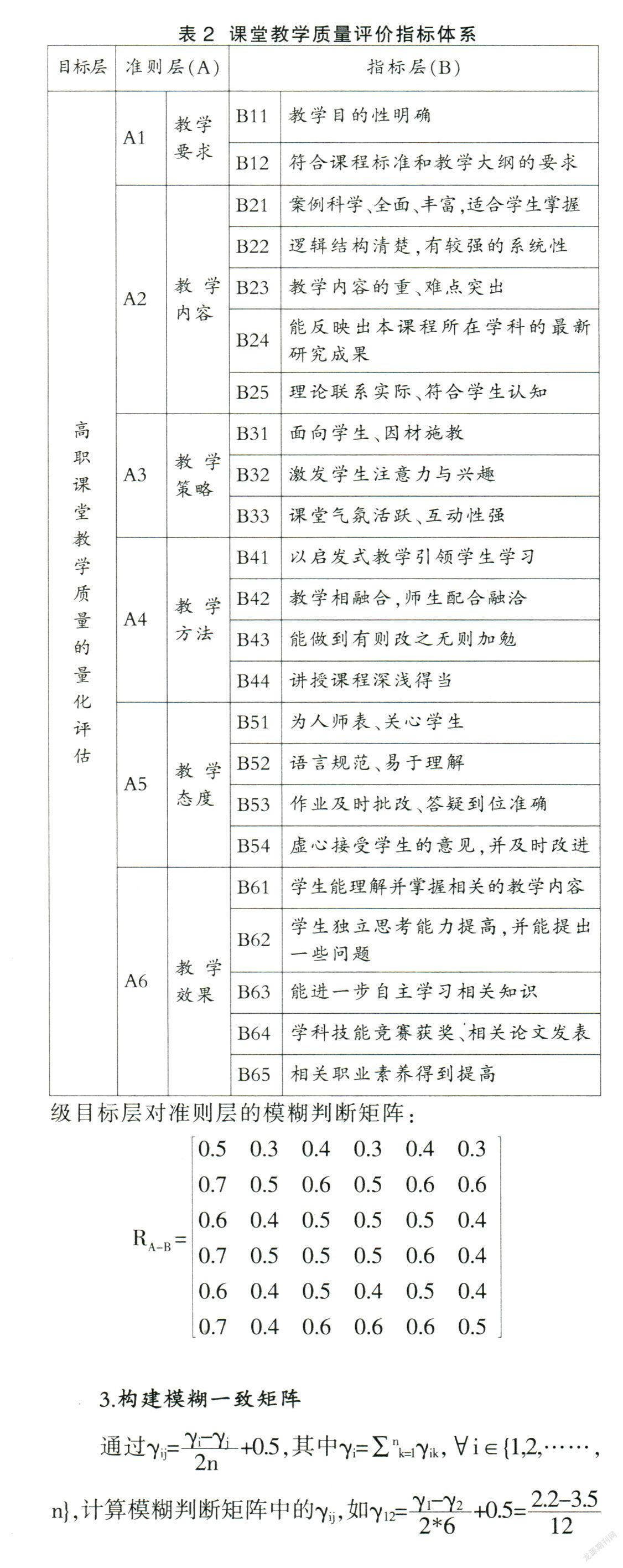
由于五类评价人员的关注点不同，对课堂教学质量评价指标也有所不同。下面以理工科课程的学生评教指标体系为例，来构建课堂教学质量评价的层次结构。对教师的课堂教学质量评价主要是针对教学要求、教学内容、教学策略、教学方法、教学态度、教学效果等六个方面进行判断。评价人员为教师任课班级的全体学生。确定一个合理、有效的评价指标体系有相当的难度和挑战。本文以教育部评估体系标准为基础，参考同类高职校的课堂教学质量评价指标等资料，构建了层次型课堂教学质量学生评价指标体系，如表2所示。

2.构建模糊判断矩阵

基于前述的课堂教学质量评价层次结构模型，设计出相应的调查问卷，发放给在教学方面具有丰富教学经验的专家、课堂教学优秀者、教学骨干以及教务管理人员，请他们结合自己的工作经验以及对准则层、指标层等因素的判断和比较进行填写，构造出判断矩阵RA-B。

本次调查问卷共向浙江省内12所高职院校的教务处、督导处、理工科类相关专业负责人等，发放问卷150份，回收141份，回收率94%，有效问卷135份，有效率90%。经过归纳、整理后，结合“ 0.1-0.9”数量标度得出标准层各因素间的比较矩阵和权重，由此得到一级目标层对准则层的模糊判断矩阵：

R=0.5 0.3 0.4 0.3 0.4 0.3

0.7 0.5 0.6 0.5 0.6 0.6

0.6 0.4 0.5 0.5 0.5 0.4

0.7 0.5 0.5 0.5 0.6 0.4

0.6 0.4 0.5 0.4 0.5 0.4

0.7 0.4 0.6 0.6 0.6 0.5

3.构建模糊一致矩阵

通过γij=+0.5，其中γi=∑nk=1γik，∀i∈{1，2，……，n}，计算模糊判断矩阵中的γij，如γ12=+0.5=+0.5=0.3917，以此类推可以计算得到模糊一致矩阵：

R= 0.5 0.3917 0.4417 0.4167 0.4500 0.4000

0.6083 0.5 0.5833 0.5333 0.5667 0.5167

0.5583 0.4167 0.5 0.4750 0.5083 0.4583

0.5833 0.4667 0.5250 0.5 0.5333 0.4833

0.5500 0.4333 0.4917 0.4667 0.5 0.4500

0.6000 0.4833 0.5417 0.5167 0.5500 0.5

4.层次单排序

根据模糊层次分析法第四步公式所示，计算模糊一致矩阵A的权重向量WA=（ω1，ω2，ω3，ω4，ω5，ω6），其中ωi=-+∑nk=1γik，如ω1=-+*2.2=0.11，同理可得各权重值，最后得到权重向量WA=（0.11，0.21，0.16，0.18， 0.15，0.19）T。以此类推得到指标层子权重向量WB1=（0.3，0.7）T，WB2=（0.2，0.4，0.15，0.1，0.15）T， WB3=（0.2，0.45，0.35）T，WB4=（0.3，0.25， 0.30，0.15）T，WB5=（0.15，0.25，0.3，0.3）T，WB6=（0.15，0.15，0.4， 0.2，0.1） T。

5.层次总排序

层次结构型课堂教学质量评价体系分为4个层次。现设目标层为O，准则层为A，指标层为B，方案层为P，根据模糊层次分析法第五步公式，可以计算出指标层B各因素相对于总目标的各子权重，其值为

WA=WB1 0 0 0 0 0

0 WB2 0 0 0 0

0 0 WB3 0 0 0

0 0 0 WB4 0 0

0 0 0 0 WB5 0

0 0 0 0 0 WB6

WA=（0.033，0.077，0.042，0.084，0.032，0.021，0.031，0.072， 0.056，0.054，0.045，0.054，0.027，0.0225，0.0375，0.045，0.02850，0.0285，0.0076，0.038，0.019）。

四、利用模糊综合评价得到定量数据

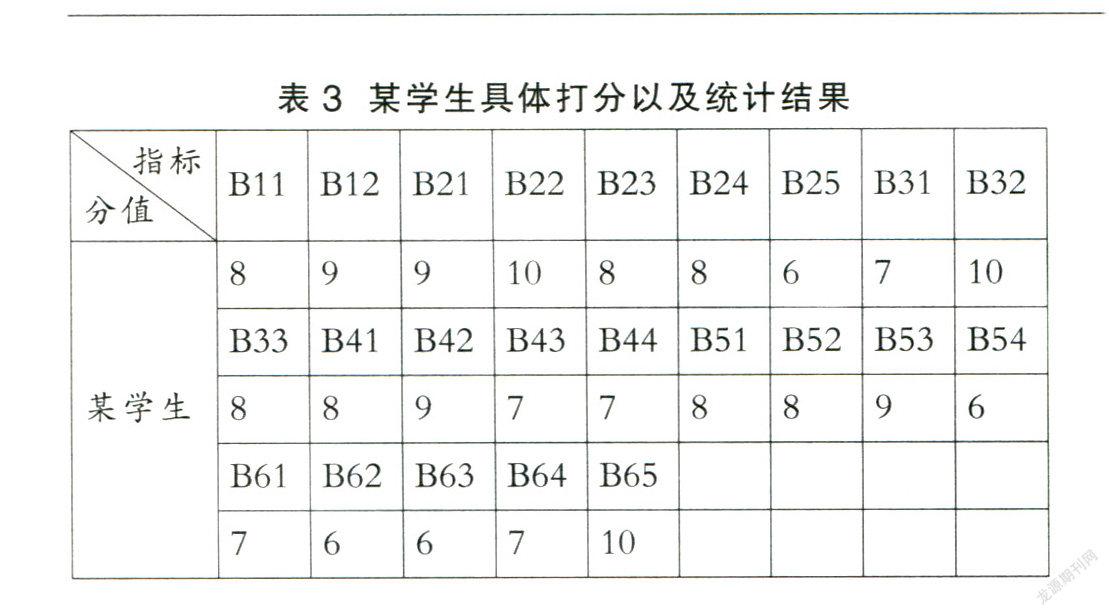
以本学院A教师为例，其负责B班级的C课程。对于A教师的课堂教学评价量化分值主要由专业教师、企业技术骨干、课程组内部成员、教学督导、学生等五类人员对该教师课堂教学指标层给出客观的评价，每个指标评价分10分制。下面以学生评教为例。某学生按照指标层进行打分，具体见表3。

使用模糊综合评价最后得到结果为8.0245，而单纯的取平均值，最后结果为7.869。如果以9.5分以上为优秀，8分到9.5分为良好，那么这位学生对A教师的评价就有了质的变化，而事实上也是如此。如B25：“理论联系实际、符合学生认知”和B32：“激发学生注意力与兴趣”，一个是6分，另一个是10分，学生其实非常在乎激发他们的兴趣，而并不是非常能体会到自己的认识是否到位。因此，这两个因素的权重几乎相差一倍（B25：0.031，B32：0.072），由此也证明模糊层次法在评价方面的有效性与客观性。

通过使用FAHP，还能够得到五类人员对于课堂教学评价影响因素的权重，并最终计算得到该课程授课教师的整体评价分值。

五、学生评教分值的客观化计算

一般来说，在统计一个班级全体学生的学评教分数时，往往不会考虑一些学生主观上的问题：如上课出勤率不高，提交作业不及时，与教师互动较少以及上课关注度不够等情况，而这些因素会直接影响学生评教的分数。因此，在学生评教完成之后，不能直接以全体学生评教分的平均分来计算最后的成绩，而是应该通过加权系数的方式来考虑因学生课堂表现所致的影响因素。

学生课堂表现影响因素系数主要包括以下4方面：出勤率、作业完成率、提问率、课堂关注率。根据教育专家、教学督导、任课教师组成的专业团队对以上4个因素进行模糊层次分析，通过四步骤进行计算，最后得到学生课堂影响因素系数的权重矩阵S=[0.35 0.3 0.2 0.15]。

通过对学生上课出勤次数、请假次数以及迟到早退次数，对学生提交作业数量以及相应的质量，对学生课间提问数量与质量等课堂行为进行统计，以及对学生课堂关注度进行分析，最后得到学生的课堂影响因素各个数值，加权之后得到最终的课堂影响因素数Qs。设每个学生的课堂影响因素系数为∀i∈{1，2，……，n}，取出该班级中课堂影响因素最大数，并计为Qsmax，将Qs归一化处理，得到Ti，步骤如下：

第一步：得到该班级中课堂影响因素最大数Qsmax。

第二步：该班级中每个学生的课堂影响因素数Qs与Qsmax进行比较得到Pi=，∀i∈{1，2，……，n}。

第三步：计算每个学生的课堂影响因素系数Ti，Ti=，∀i∈{1，2，……，n}。

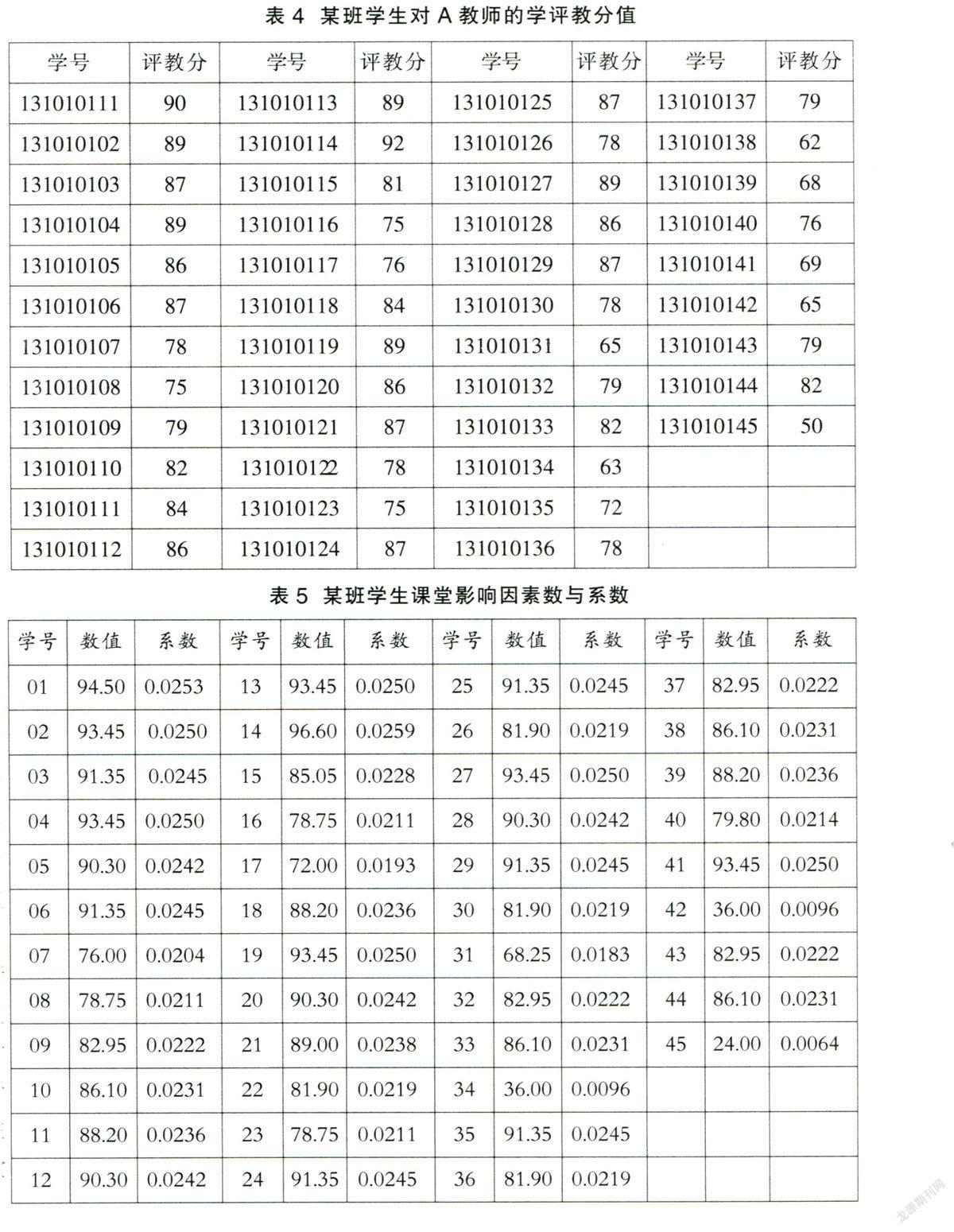
通过以上三步计算得到每个学生的课堂影响因素系数Ti，再将Ti与学评教的数值进行乘积，最后得到加权学生课堂影响因素系数后的学评教乘积。表4是B班级对A教师所上的C课程所作的学生评教数据。该班共有45位学生，具体数据见表4学评教分值。

通过学院自主开发的“课堂教学质量量化系统” 所采集到的相关数据，可计算每个学生的课堂影响因素系数Ti，见表5学生课堂影响因素系数。

最后通过计算得到以下数据：学生评教的算术平均值为79.67，加权学生课堂影响因素系数之后得到的值为82.71，通过分析发现，大部分评教分数较低的学生，其课堂影响系数也较低，因此，在计算过程中其所占的权重较少。通过这一计算方法的客观化处理，使得学生评教的结果更准确与更符合实际。

模糊层次分析评判具有客观、层次清晰和计算简便等特点，具有较好的操作性与实用性。本文通过FAHP构建高职课堂教学质量的量化评价模型，得到了课堂教学质量各因素的权重指标以及各类评价人员的权重系数，特别是对学生评教分的计算方法进行了客观化的模糊处理，从而使评教过程更加贴近实际，评价的结果更客观。

参考文献：

[1]张炳江.层次分析法及其应用案例[M].北京.电子工业出版社，2014.

[2]Diego Falsini ， Federico Fondi ，Schiraldi et al. A logistics provider evaluation and selection methodology based on AHP， DEA and linner programming integration[J].International journal of production research，2012，50（17）：4822-4842.

[3]王秀明，陈明锐.AHP层次分析法在高校师资队伍综合评价系统中的应用[J].海南大学学报（自然科学版），2012，30（3）：277-281.

[4]邓雪.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识，2012，42（7）：94-96.

（编辑：鲁利瑞）