基于有效模态质量优选法的机载雷达随机振动分析*

李 钊，王志海

(中国电子科技集团公司第三十八研究所， 安徽 合肥 230088)

基于有效模态质量优选法的机载雷达随机振动分析*

李 钊，王志海

(中国电子科技集团公司第三十八研究所， 安徽 合肥 230088)

随着现代电子设备不断向集成化、模块化和一体化方向发展，对于振动环境异常复杂的航空航天电子设备，系统级随机振动环境可靠性分析是决定结构总体设计方案成败的重要因素。针对某机载雷达系统结构的随机振动问题，建立一套基于有效模态质量优选法的随机振动分析技术，通过对复杂系统的合理简化以及优选法相关参数的细致考评，快速有效地获取系统级的随机振动响应，分析结果可为结构总体设计方案提供理论基础和设计指导，并为插件级或元件级结构设计提供载荷输入。

电子设备；随机振动；有效模态

引 言

振动环境可靠性是影响电子设备工作状态和寿命的主要因素[1]。由于振动产生的共振或疲劳，可能导致电性能下降、零部件失效、疲劳损伤甚至破坏的现象[2-3]。随着现代电子设备不断向集成化、模块化和一体化方向发展[4-5]，对于振动环境异常复杂的航空航天电子设备(频率范围：10～2 000 Hz)，系统级随机振动环境可靠性分析是决定结构总体设计方案成败的重要因素，必须在方案设计阶段予以重点考虑和论证。传统上采用的设计-试验-改进方法，周期长、成本高，并且由于试验条件的限制，无法全面获得系统各个部位的振动响应，因此也难以系统指导设计[6]。基于模态叠加法的随机振动分析技术在进行复杂电子装备系统校核时，往往由于所考察频率范围内重复插件存在过多的相近局部模态，从而导致极高的计算成本，无法快速获取结构的随机振动响应，同时对于复杂系统薄弱结构缺乏有效直接的物理判断[7]；针对性地对系统结构进行模型简化虽然可以有效降低计算成本，但准确获取系统振动特性取决于对系统结构特性的准确判断以及恰当的简化方式，不合理的简化常常引起系统振动响应的显著偏差[8-9]。

本文针对某机载雷达系统结构的随机振动问题进行研究，建立一套基于有效模态质量优选法的随机振动分析技术，通过对复杂系统的合理简化以及优选法相关参数的细致考评，快速有效地获取系统级的随机振动响应，分析结果可为结构总体设计方案提供理论基础和设计指导，并为插件级或元件级结构设计提供载荷输入。

1 机载雷达结构有限元模型

本文以某机载雷达为分析对象，该雷达为满足机载系统对体积和重量的要求，采用模块化、一体化设计，包含微带天线、天线骨架、T/R、风机、波控、电源和天线罩等。其中T/R、风机由数十个模块化的重复插件构成，且为了便于装配，骨架箱体结构设计了较多的安装板，因此该电子设备包含了大量的重复插件和板壳结构。建立包含所有结构细节的分析模型非常耗时耗力，同时对于分析其总体设计方案也是不必要的，因此本文通过以下原则对该机载雷达结构进行了模型简化：

1)天线骨架结构直接决定了系统的主要振动特性，有必要对其进行准确模拟；

2)对于系统振动特性影响较小的电子设备单元采用质量等效，通过合理分配质量使得模型重心与实际匹配；

3)为了拆装简便，结构大量采用螺钉连接，总体方案论证时采用刚性单元对其进行模拟，可描述结构整体振动特性；

4)有限元网格尺寸应满足高频计算要求，同时兼顾计算成本；

5)结构主要为金属铝材料，材料临界阻尼比取0.03。

基于上述模型简化原则，采用ABAQUS有限元软件建立如图1所示的机载雷达结构的有限元模型。

针对不同部件分别采用壳单元、质量单元和刚性单元进行模拟，其中壳单元用以模拟结构中的腔体、肋板等；结构中不参与承力的电子设备采用质量单元进行等效简化；相关部件间的连接方式为刚性连接。整个有限元模型包含139 751个壳单元和40 248个质量单元，共128 252个节点，总重约60 kg，与设计质量相符。

2 基于有效模态质量优选法的随机振动分析技术

2.1 有效模态质量

无阻尼多自由度系统的自由振动方程[10]为

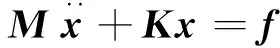
(1)

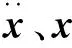
(K-ω2M)φ=0

(2)

式中：ω为系统各阶频率；φ为所对应的各阶振型。第i阶模态在自由度j(j=1, 2, …, 6)上的模态参与因子为

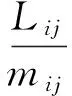
(3)

式中：L=φTMγ，γ为影响矩阵，表示结构基础的单位静位移使各个质点所产生的位移；m=φTMφ，为对角化的模态质量矩阵。第i阶模态在自由度j上的有效模态质量为[11-12]

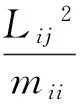
(4)

在平动方向上，各方向所有模态的有效模态质量之和等于系统总质量；在转动方向上，有效模态质量之和等于系统总转动惯量。各阶模态的有效模态质量系数为有效模态质量与系统总质量或系统总转动惯量的比值，即

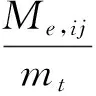
(5)

通常情况下，有效质量大的模态容易被基础激励，而有效质量小的模态不易被基础激励，因此某阶模态的有效模态质量系数直接反映了该阶模态对整个结构贡献的大小。

2.2 优选法

对于包含大量相近局部模态的复杂电子装备，有效识别总体模态和局部模态，并判定每阶模态在相应振动方向上的贡献大小，对于合理制定随机振动分析策略至关重要。为此，本文提出了基于有效模态质量优选法的随机振动分析技术，它以有效模态质量为依据，对复杂系统振动特性进行合理的物理判断和简化，能在大幅减小计算成本的同时保证较高的计算精度。该技术主要包括模态试算、模态优选和随机振动计算3个步骤，其详细分析流程如图2所示。

图2 基于有效模态质量优选法的随机振动分析流程

(1)模态试算

利用建立的有限元模型进行前n阶模态试算，初始值n0=50。通过3个随机振动方向(前后方向、上下方向和左右方向，分别命名为X、Y和Z)上有效模态质量系数的累计判断当前模态分析的阶数是否足够描述系统的随机振动特性，判据为3个方向的累计有效模态质量系数ηX、ηY、ηZ均大于临界系数ηX,C、ηY,C、ηZ,C，即

(6)

如不满足判据条件，则模态阶数n=n+50，重新进行模态试算；如满足判据条件，则结束模态试算，以当前模态分析的各阶模态进行模态优选。关于该判据中的临界系数，下文将对此进行数值考评。

(2)模态优选

对3个随机振动方向(X、Y和Z)分别采用最小有效质量剔除原则进行模态优选，即首先剔除各阶有效模态质量中模态质量最小的模态，而后检查各方向的累计有效模态质量系数是否仍大于临界系数，如满足则继续剔除剩余各阶有效模态质量中模态质量最小的模态，如不满足则保存前一步的优选模态，完成模态优选过程。

(3)随机振动计算

首先根据电子设备的工作平台确定其3个方向(X、Y和Z)的振动功率谱WX、WY和WZ，然后利用指定频率范围的优选模态选择合适的频率计算点数m，并最终利用ABAQUS有限元分析软件的线性摄动算法进行基于基础激励的随机振动计算。

为提高计算效率，上述基于有效模态质量优选法的随机振动分析流程采用ABAQUS Python脚本语言实现自动化处理。

3 参数考评

由上可见，基于有效模态质量优选法的随机振动分析技术包含两个重要参数，累计有效模态质量临界系数ηX,C、ηY,C、ηZ,C和频率计算点数m，其中ηX,C、ηY,C、ηZ,C反映描述复杂电子设备系统所采用的模态数量，m则反映所考察的宽频振动范围内相邻两个优选模态间频率计算点的离散程度。原则上，这两个参数取得越大，数值计算结果越精确，但相应的计算成本也越高，且随着参数的增加而急剧增加。因此，这两个分析参数的合理选取对于复杂电子设备系统随机振动分析的精度和效率将有重要影响，为此本文拟对其进行考评。

本文在机载雷达结构随机振动分析中，采用GJB 150中机载设备的振动试验条件，见图3。由于该机载雷达结构重量大于36 kg，对振动试验量值进行了相应衰减，且将垂直方向定为设备主振方向，其他非主振方向量值为主振方向的0.8倍。

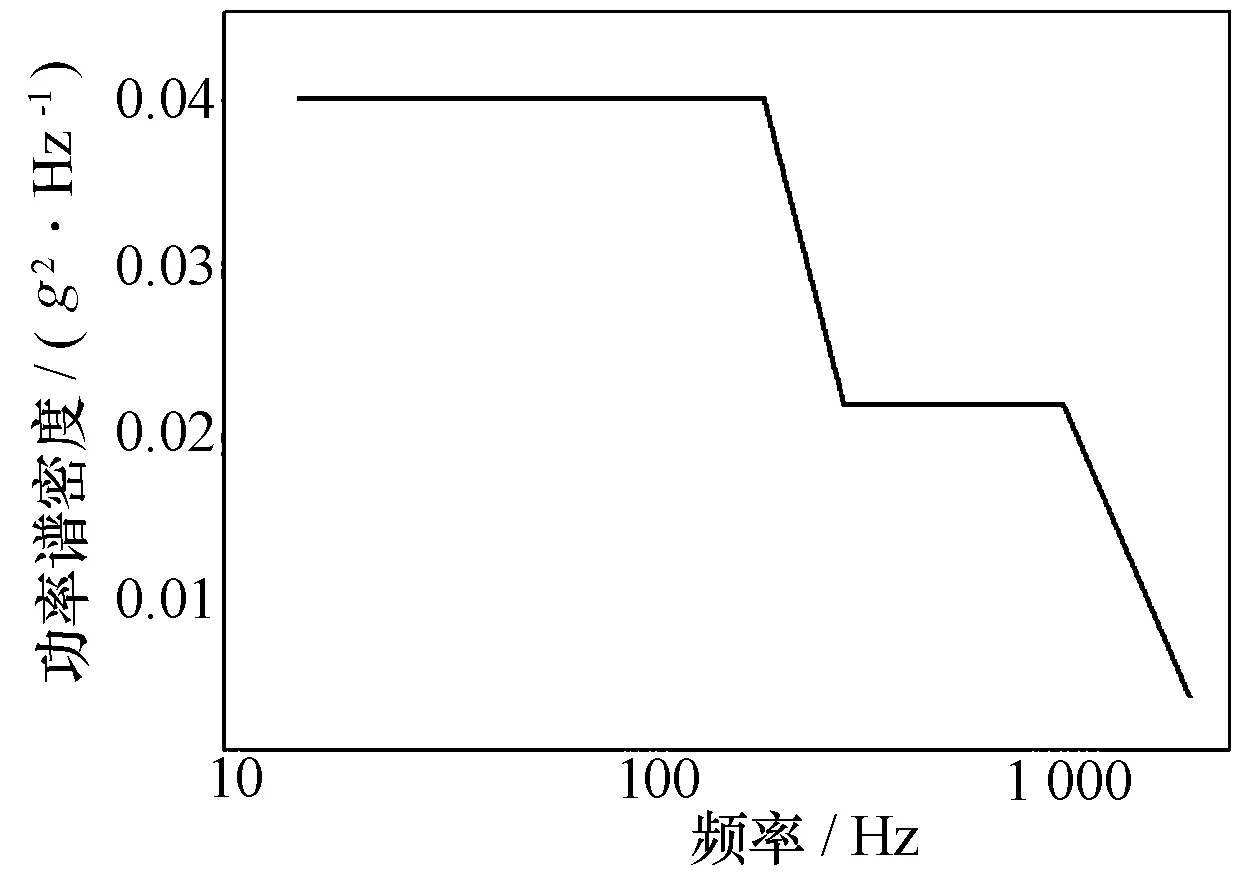
图3 机载雷达结构振动试验条件

3.1 累计有效模态质量系数

图4为计算得到的0～2 000 Hz范围内3个振动方向上的各阶有效模态质量分布情况。由图可见对于所考察的机载雷达结构，各阶模态对结构整体的贡献不尽相同。主要贡献模态虽集中在前50阶内，但在前300阶内仍包含较多有效模态质量较大的模态。盲目地选择前若干阶进行随机振动计算非常浪费计算资源，因此有必要采用优选方法对结构模态进行有效选择。同时从图中还可以看出，同一模态对于3个方向的振动贡献不同，因此在进行不同方向随机振动分析时需要分别进行模态优选。

图4 0～2 000 Hz内X、Y、Z方向有效模态质量分布

为了考察模态优选法中临界系数对计算结果的影响，在3个振动方向上试算了选取不同累计有效模态质量系数临界值时的随机振动响应，如表1所示。此外，为了保持考察参数的一致性，频率计算点数m此时均取为20。

表1 3个振动方向上不同累计有效模态质量系数临界值

图5为计算得到的3个方向随机振动响应中最大均方根Mises等效应力(RMISES)随累计有效模态质量系数临界值的变化关系，可见3个方向上的最大均方根等效应力基本上均随着临界值的逐渐提高而逐渐增加，并于90%附近时趋于稳定。图6为3个方向随机振动计算时间随累计有效模态质量系数临界值的变化关系，可见当累计有效模态质量系数临界值较小时，计算时间基本无较大变化，而随着临界值的进一步增加，计算时间急剧增加。根据图5和图6，综合计算精度和计算效率，可选取临界值为90%作为优选模态的判据。

图5 最大均方根Mises等效应力随累计有效模态质量系数临界值的变化关系

图6 随机振动计算时间随累计有效模态质量系数临界值的变化关系

3.2 频率计算点数

采用5个不同的频率计算点数分别进行Y方向随机振动分析，频率计算点数分别为m=3、m=5、m=10、m=15和m=20。图7和图8分别给出了雷达结构最大均方根等效应力和最大均方根相对位移随频率计算点数的变化关系，可见随着频率计算点数的逐渐增加，最大均方根等效应力和最大均方根相对位移初始时显著减小，而后趋于平缓，m=15和m=20两者计算结果相差已不超过1%。

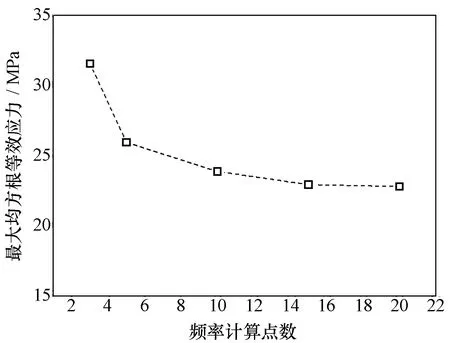
图7 最大均方根等效应力随频率计算点数的变化关系

图8 最大均方根相对位移随频率计算点数的变化关系

图9为随机振动计算时间随频率计算点数的变化关系，可见随机振动计算时间基本上随着频率计算点数的增加而线性增加。综合计算精度和计算效率，可选取m=15进行基于模态优选法的随机振动分析。

图9 随机振动计算时间随频率计算点数的变化关系

4 结果分析

根据上述参数考评结果，采用累计有效模态质量系数临界值为90%、频率计算点数为15进行某机载雷达结构的随机振动分析。

以主振动方向为例，图10、图11和图12分别给出了上下方向随机振动时雷达结构均方根加速度分布(Y向)、均方根位移分布(Y向)以及均方根Mises等效应力分布。由分析结果可以看出：雷达结构均方根加速度和均方根位移较大区域均位于盖板处，最大均方根加速度(Y向)约为5.71g，最大均方根位移(Y向)约为0.98 mm，满足结构刚度设计要求；雷达结构整体应力分布比较均匀，最大均方根Mises等效应力为20.1 MPa，具有较高的安全裕度，结构强度设计比较合理。

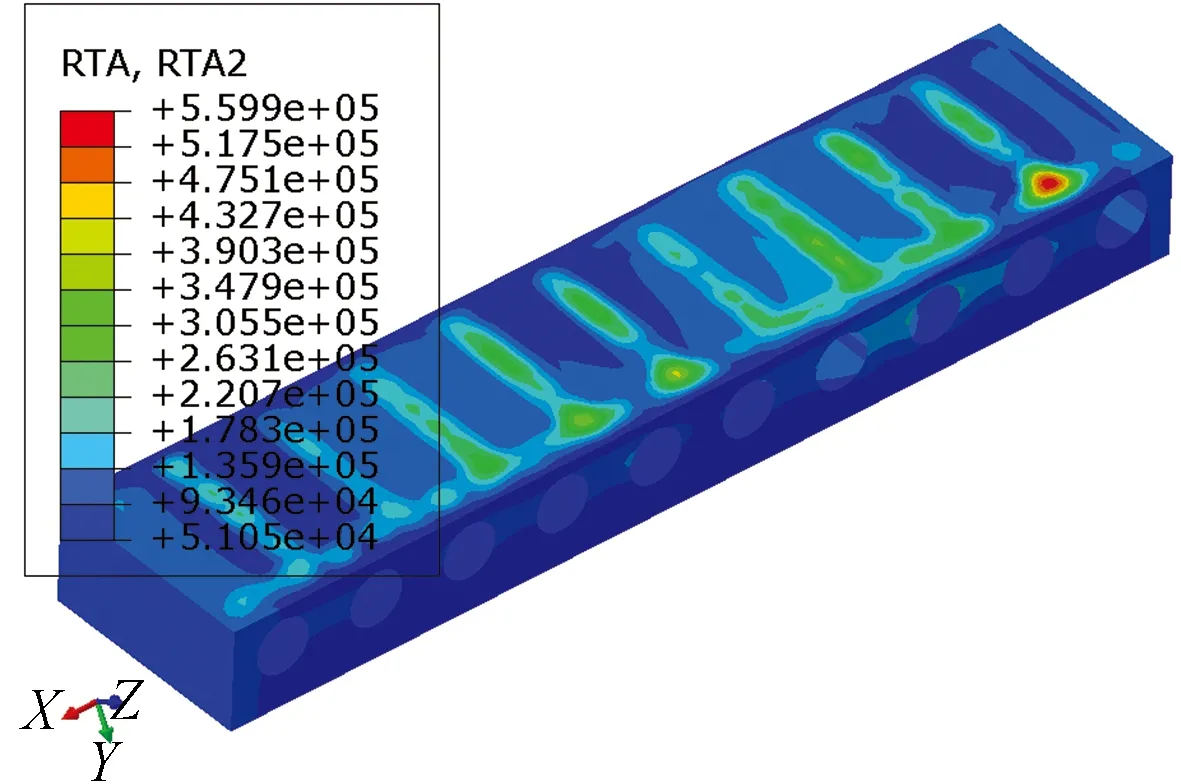
图10 上下方向随机振动时Y向均方根加速度分布

图11 上下方向随机振动时Y向均方根位移分布

图12 Y向随机振动时均方根等效应力分布

图13 特征点分析

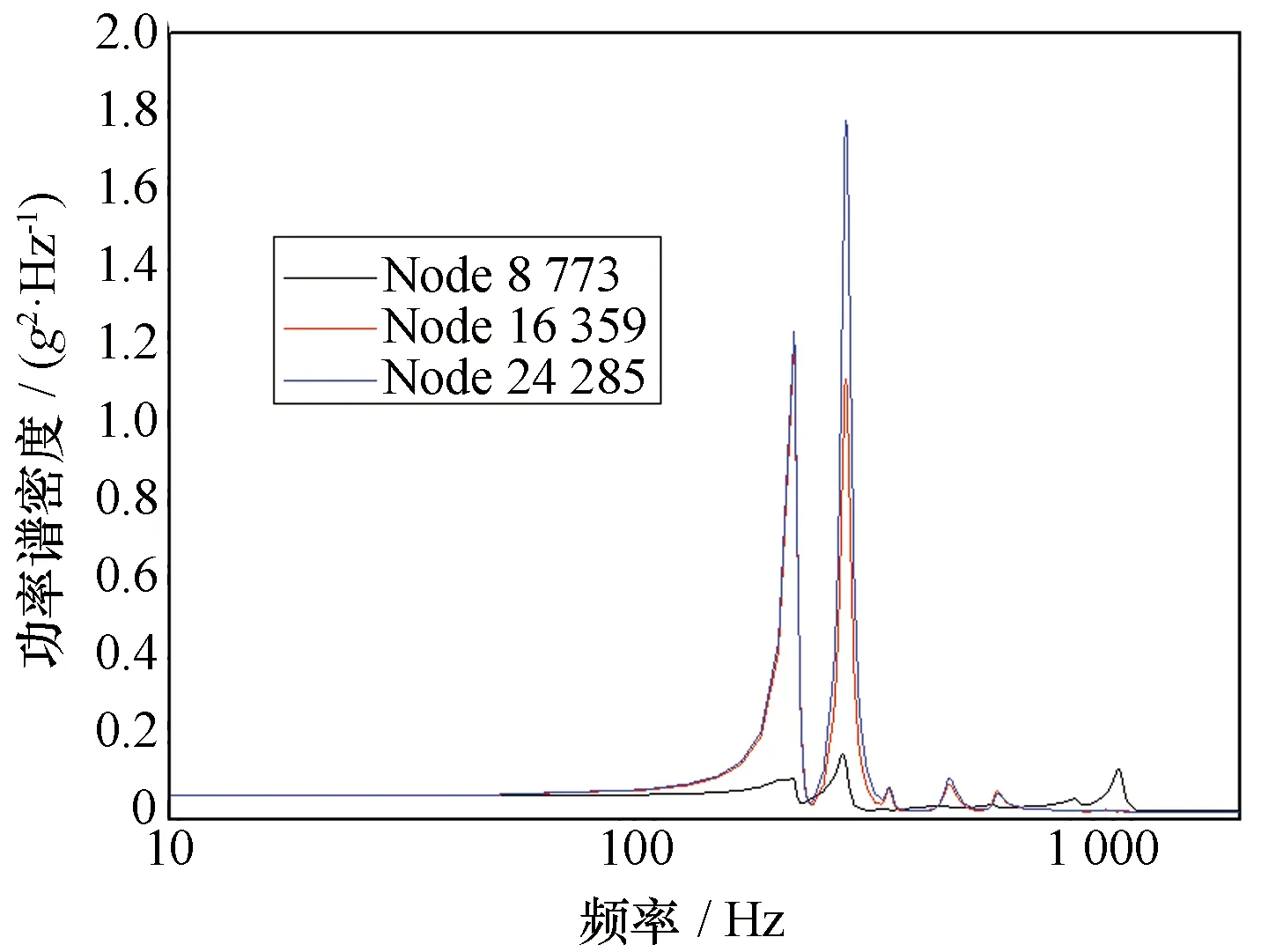
图14 加速度频率响应曲线

图15 位移频率响应曲线

为了考察系统中几个关键位置的随机振动响应，为插件级或元件级结构设计提供载荷输入，本文提取了图13所示的T/R安装板、天线阵面和骨架3个特征点的功率谱密度和均方根位移响应曲线，如图14和图15所示。由分析结果可见，整体上T/R安装板处特征点的功率谱密度较小，骨架特征点的功率谱密度较大；3个特征点的功率谱密度在219 Hz和284 Hz附近出现了较大的峰值，即发生了共振响应；3个特征点的均方根位移响应基本一致，当频率达到130 Hz附近时均趋于稳定。

5 结束语

1)提出一套基于有效模态质量优选法的随机振动分析技术，形成了包括模态试算、模态优选和随机振动计算的分析流程；

2)对累计有效模态质量系数临界值和频率计算点数进行了数值考评，确定选取ηX,C=ηY,C=ηZ,C=90%、m=15时，满足计算精度和计算效率的要求；

3)获得某机载雷达结构随机振动响应，可为结构总体设计方案提供理论基础和设计指导。

[1] STEINBERG D S. Vibration Analysis for Electronic Equipment[M]. 2nd Edition. New York: John Wiley and Sons, 1988: 414-420.

[2] 李春洋, 陈循, 陶俊勇, 等. 基于模态分析的印制电路板振动可靠性研究[J]. 中北大学学报：自然科学版, 2007, 28(2): 156-160.

[3] 刘衍平, 张刘斗, 高新霞. 电子设备机柜随机振动试验的数值模拟[J]. 塑性工程学报, 2007, 14(4): 151-155.

[4] 宋增志. 电子装备综合一体化技术研究[J]. 无线电工程, 2007, 37(7): 41-43.

[5] 胡云. 机载电子设备可靠性与结构一体化设计方法[J].电讯技术, 2012, 52(9): 1532-1536.

[6] 殷雪岩. 随机振动试验技术研究[J]. 北京航空航天大学学报, 1995, 21(4): 119-123.

[7] 石进峰, 吴清文, 郭万存, 等. 基于有效模态质量的有限元建模[J]. 系统仿真学报, 2013, 25(5): 995-998.

[8] PITARRESI J M, PRIMAVERA A A. Comparison of modeling techniques for the vibration analysis of printed circuit cards[J]. ASME Journal of Electronic Packaging, 1992, 114(4): 378-383.

[9] WILSON E L. Three-dimensional Static and Dynamic Analysis of Structures[M]. 3rd Edition. Berkeley: Computers & Structures Inc., 2002: 170-175.

[10] RAO S S. Mechanical Vibrations[M]. 5th Edition. Upper Saddle River, New Jersey: Prentice Hall Inc., 2011.

[11] CLOUGH R W, PENZIEN J. Dynamics of Structures[M]. 3rd Edition. Berkeley: Computers & Structures Inc., 1995: 623-646.

[12] APPEL S. Calculation of Modal Participation Factors and Effective Mass with the Large Mass Approach[R]. Berlin, Heideberg, Germany: Springer, 1992: 1654-1661.

李 钊(1985-)，男，博士，工程师，主要从事雷达结构仿真与测试工作。

王志海(1981-)，男，博士，高级工程师，主要从事雷达结构仿真与优化设计工作。

Random Vibration Analysis of Airborne Radar Based on Modal Mass

LI Zhao，WANG Zhi-hai

(The38thResearchInstituteofCETC,Hefei230088,China)

With the constant development in the direction of integration, modularization and unification of modern electronic devices, reliability analysis of system-level random vibration environments is an important factor in determining the success or failure of overall structure design scheme for aerospace electronic devices under very complex vibration environments. Studies on the random vibration of the structure of an airborne radar system are carried out, and a set of random vibration analysis techniques based on the optimization of effective modal mass are established. By reasonable simplification of complex systems as well as detailed evaluation of relevant parameters of the optimization, system-level random vibration responses are acquired rapidly and effectively. The analysis results can provide theoretical basis and design guidance for overall structure design scheme, and supply load input for plug-in-level or component-level structure design.

electronic device; random vibration; effective mode

2014-11-05

国家科技支撑计划(2011BAH24B05)

TB123；TN959.73

A

1008-5300(2015)01-0001-06