小行星重力场全球及局部球谐系数计算与仿真

郭延宁，李晓宇，马广富，崔祜涛

(1.哈尔滨工业大学控制科学与工程系，150001哈尔滨;2.哈尔滨工业大学深空探测基础研究中心，150001哈尔滨)

近年来，作为深空探测重要组成部分，小行星探测活动从早期的近距离飞越、低空绕轨探测［1］，发展至目前的悬停［2］、表面软着陆和采样返回［3］，对于推动科学技术进步和帮助人类了解宇宙发展等有重要科学意义［4］.受质量小、形状不规则、自旋复杂等因素影响，小行星重力场与传统近球形大行星或天然卫星重力场存在极大差异.因此高精度的重力场建模不仅是研究设计小行星卫星轨道所需要解决的首要问题，也是小行星探测任务的主要科学目标之一.

小行星重力场建模方法的研究已经有一百多年历史，方法众多［5］，目前最为广泛使用的是球谐函数模型［6］与多面体模型［7］.球谐函数模型计算效率高、易于解析表达，可根据各阶次球谐系数计算出小行星非球形引力摄动，便于轨道设计.但在布里渊球域内发散，且存在截断误差.多面体模型可进行重力场的高精度建模，无发散区域，且能提供检验点相对小行星的位置信息，但因其是数值算法，不能给出受摄轨道解析式，计算量大，存在一定的局限性.实际使用的球谐系数大都是由轨道数据解算出来的［8］，而对于还未进行实际探测任务的小行星无法得到精确值.

针对小行星球谐系数的获取问题，大多采用三轴椭球体模型法，计算由小行星简化的椭球体的球谐系数，以此近似代替小行星的球谐系数［9］.可见小行星的形状越不规则，误差将越大.Scheeres［9］和胡维多等［10］以小行星二阶二次重力场为出发点对小行星附近的动力学情况进行了研究，并利用小行星的三个主轴转动惯量唯一确定球谐系数的二阶项，但未给出高阶项结果.张振江等［12］提出一种基于多面体模型的不规则形状小行星重力场球谐系数求取方法，不仅提高了重力场建模的精度，同时可求其高阶系数.但就计算过程中检验点的选取规则、多面体模型的划分形式以及局部重力场建模等问题并未进行讨论.较小行星重力场问题而言，地球的重力场研究已很成熟.众多优秀学者［13-14］先后研究了适于描述地球重力场全球特性的全球模型和能够精确构建局部地区重力场的局部模型.

鉴于此，本文在已有研究基础上进一步研究了小行星重力场球谐系数的计算及优化问题.首先，分析说明了检验点的均匀分布形式和等面划分的均匀多面体模型可以提高全球球谐系数的计算精度.随后，为获得高精度的局部重力场模型，提出局部球谐系数概念，并通过建立新的性能指标检验基于此组系数的球谐函数法在布里渊球域内的可行性，有效拓展了球谐函数法的应用范围.最后，以小行星Eros433为实际算例，计算了全球及局部球谐系数，验证本文方案的有效性和准确性.

1 重力场模型与球谐系数的求取

1.1 重力场模型

1)球谐函数模型.利用球谐函数描述的重力势能函数为［5］

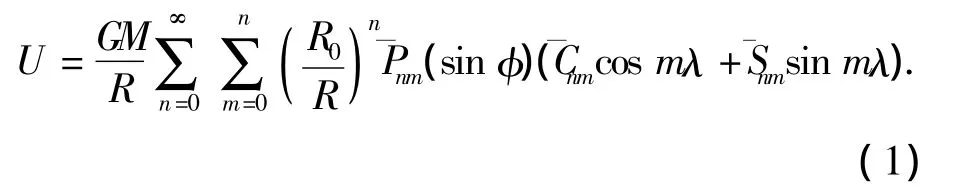
其中:G是万有引力常数;M是小行星质量;R0是布里渊球半径;是标准缔合勒让德多项式;是标准球谐系数;n、m是多项式阶数、次数;R、φ、λ是检验点到中心天体质心的距离、纬度和经度.

将U对位置矢量求一阶偏导数，可得重力加速度为

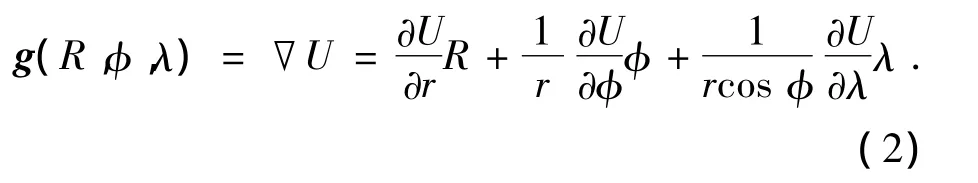
其中:

2)多面体模型.利用多面体模型描述的重力势能函数为［7］

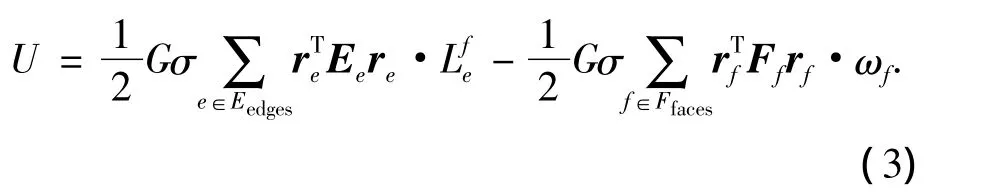
其中Eedges和Ffaces分别表示多面体模型的边集合与面集合.

对应重力加速度函数为

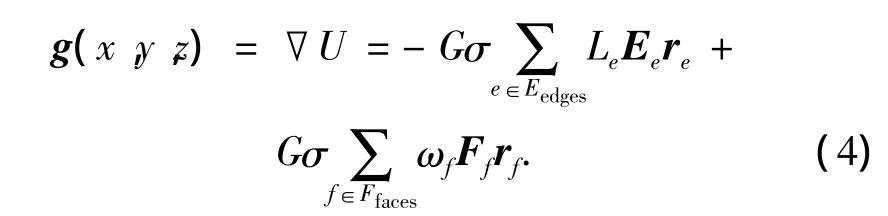
其中:σ为天体密度;e表示边;f表示面，向量是由检验点指向表面任一点的位置矢量;re是由检验点指向多面体边上任一点的位置矢量.

1.2 球谐系数计算方法

对于未探测的星体，在小行星固连坐标系下，通过引入势能值的虚拟观测量，求解由球谐函数描述的势能的拉普拉斯方程即可得到球谐系数.

任给一检验点Ri=(λi，φi，ri)，对于不规则形状小行星利用多面体模型算得该检验点处的势能作为势能虚拟观测量Ui，对于形状规则的、势能可解析表达的小行星，Ui用解析值代替，根据式(1)，则可构造一个以和为变量的方程［12］:

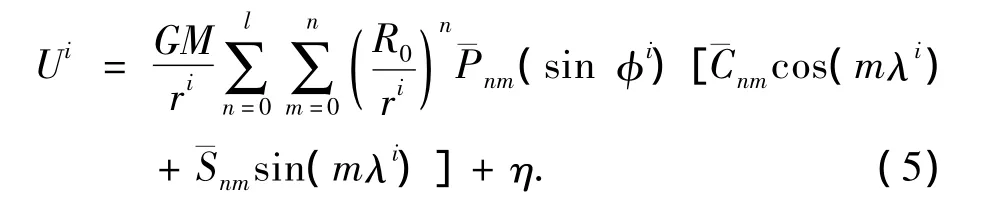
其中方程未知量的个数为l(l+2)(0无意义，为0，00为1).理论上只要在小行星势能场中选取l(l+2)个不同的检验点建立线性方程组，构成Ax=b形式，就可以求解出共l(l+2)个的变量和但由于方程系数存在因子(R0/ri)nnm(sinφi)，使得检验点选取时无法确保方程线性无关.所以在实际计算过程中，通过增加方程个数组成超定方程，再求出此超定方程的最小二乘解来解决上述问题.

2 全球球谐系数

本文将基于小行星全球信息得到的球谐系数称为全球球谐系数，即传统意义上的球谐系数，其流程如图1.因其满足球谐函数的基函数具有整个空间域上的正交性，因此用它来描述的函数刻画的都是全空间上的性质，适用于小行星布里渊球域外任意位置.利用精确的全球球谐系数表示的重力场全球模型可以比较直观地反映出小行星某些全球性特征.

图1 全球球谐系数研究流程

2.1 多面体模型面数的选取

鉴于匀质三轴椭球体重力场具有解析表达且存在高阶球谐系数，以椭球体为例进行分析和验证.

椭球体的球谐系数解析表达式如下［12］:

1)当n、m为所有正整数时，Snm=0;

2)当n或m为奇数时，Cnm=0;

3)当n、m为其他情况时

式中克罗内克符号

取椭球体半长轴a、b、c分别为16、8、6 km，密度为2.7 g/cm3，则布里渊球半径R0为16 km.本文将星体表面用面积大小相当的三角形剖分得到的多面体模型称为均匀多面体模型，上述椭球体多面体模型如图2.分别取面数N为760、20 000和54 000，计算椭球体球谐系数，结果见表1.

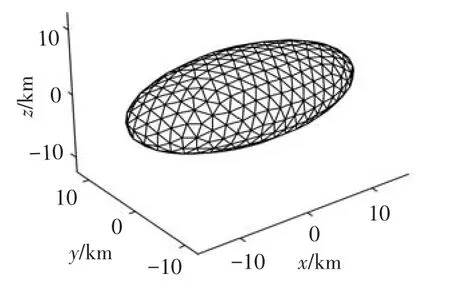
图2 匀质椭球体均匀多面体模型

表1 椭球体不同面数球谐系数计算结果

由表1结果可知，随着多面体模型面数的增加，模型越逼近真实形状，计算得到的球谐系数结果也越精确，但以牺牲计算效率为代价.

2.2 检验点选取方式

大量计算表明，检验点选取方式将直接影响球谐系数的计算精度.图3给出了检验点的四种选取方式，固定相同的检验点个数(总数均为700个)和包络体形状(球体，且半径为20 km)，图中网格交点即为检验点:1)检验点均匀分布在球面上;2)检验点集中z轴两端，对应椭球体南北两极附近;3)检验点集中在x轴两端，对应椭球体长轴两端;4)检验点集中在椭球体北极上空.

采用上述检验点选取方式求解椭球体球谐系数，其中多面体模型面数N为54 000，所有选取方式对应的计算结果见表2.

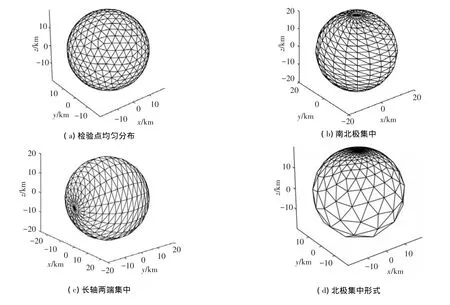
图3 检验点选取方式

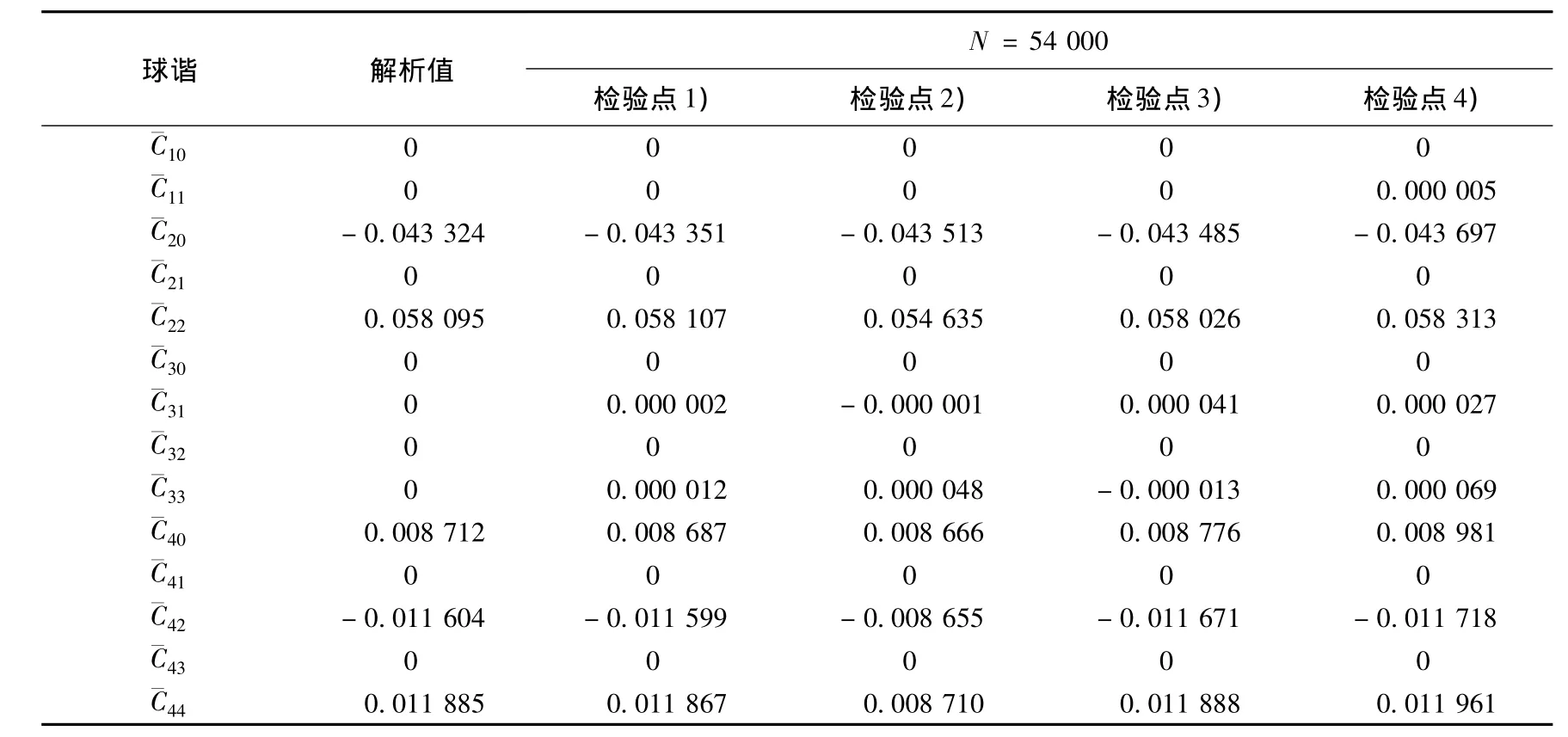
表2 椭球体不同检验选取方式求解椭球体球谐系数

由表2计算结果易知，选取均匀分布的检验点(1)进行计算，可以得到相对其他方式更加精确的结果，各项相对误差更小，全局取点方式优于局部取点方式.

2.3 多面体模型划分形式

下面将椭球体表面由经纬度信息构成的四边形网格结构分割成三角形，由此得到的多面体模型表面各三角形大小不一，这里简称为非均匀多面体模型，如图4所示.为与均匀多面体模型进行比较分析，计算N=54 000的非均匀多面体模型球谐系数，结果见表3.

图4 非均匀多面体模型

由表3可知，均匀多面体模型要优于非均匀多面体模型，前者20、22相对误差仅为0.062 3%、0.020 7%，而 后 者 结 果 分 别 为 0.203 1% 和0.084 3%.非均匀多面体的三角形面积大小不均，位于南北两极的三角形面积极小且相当密集，而在赤道附近，尤其长轴两端处，三角形面积较大，分布稀疏，这就使得在相同面数条件下均匀模型更加精准的逼近小行星不规则形状，进而得到更加精确的重力场模型.不过，理想椭球体仅为一特殊情况，对于实际的小行星而言，如何逼近其真实形状的划分方法并不绝对，如在平坦地区可以采用大三角块，而在崎岖地区建议细化分割.

表3 椭球体不同多面体模型球谐系数计算结果

3 局部球谐系数

针对探测器活动在某一特定空间范围时，特别是在布里渊球域内，全局球谐系数往往不能满足精度和效率的计算需求.因此本文借鉴地球重力场局部模型的概念，通过在特定活动区域集中选取检验点，求取局部球谐系数.引入局部球谐系数不旨在得到更加精确的全球重力场，而是以提高该局部区域重力场计算精度、增强轨道定轨和预报精度为目的.传统的球谐函数法只适用于布里渊球域之外，而局部球谐系数模型可用于任意局部空间，不存在任何局限性.

为验证局部球谐系数模型的性能优势，在探测器活动区域选取轨道，抽取测试点，利用局部球谐系数模型求其势能值，并与真实值进行分析比较.其研究流程如图5所示.

为衡量局部球谐系数对局部活动区域势能场的拟合程度，定义性能指标如下:

其中:N为轨道上测试点的抽取数目是局部球谐系数模型计算得到的测试点势能值;U是测试点的真实势能值，若小行星形状规则，使用其解析解，若小行星形状不规则，利用多面体模型结果近似代替真实值.PI越接近于1，说明结果拟合程度越高.

下面，仍以椭球体为例进行讨论.

图5 局部球谐系数研究流程

3.1 布里渊球域外局部球谐系数

以探测器活动区域集中在椭球体北极上空为例.因椭球体势能场是解析的，此处，以其解析值［5］为式(5)左侧的势能虚拟观测值，并利用图3的(a)、(b)、(c)三种检验点方式，算得球谐系数见表4.为考察局部球谐系数性能，选取椭球体北纬85°，高度25 km处的盘旋轨道(见图6)，分别抽取不同数目的测试点，计算PI，结果见表5.

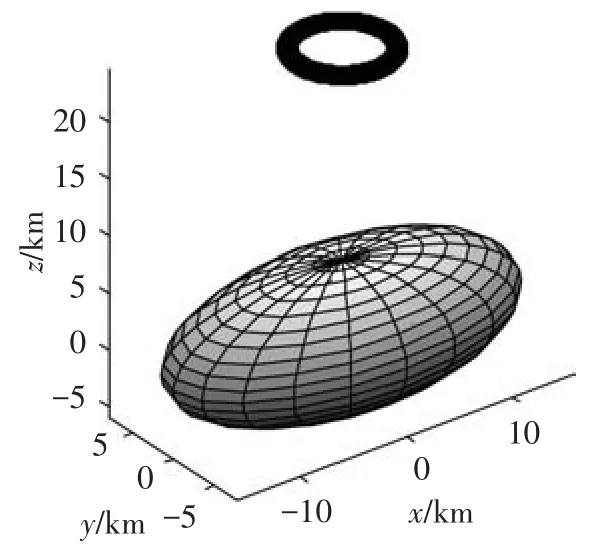
图6 北极上空盘旋轨道

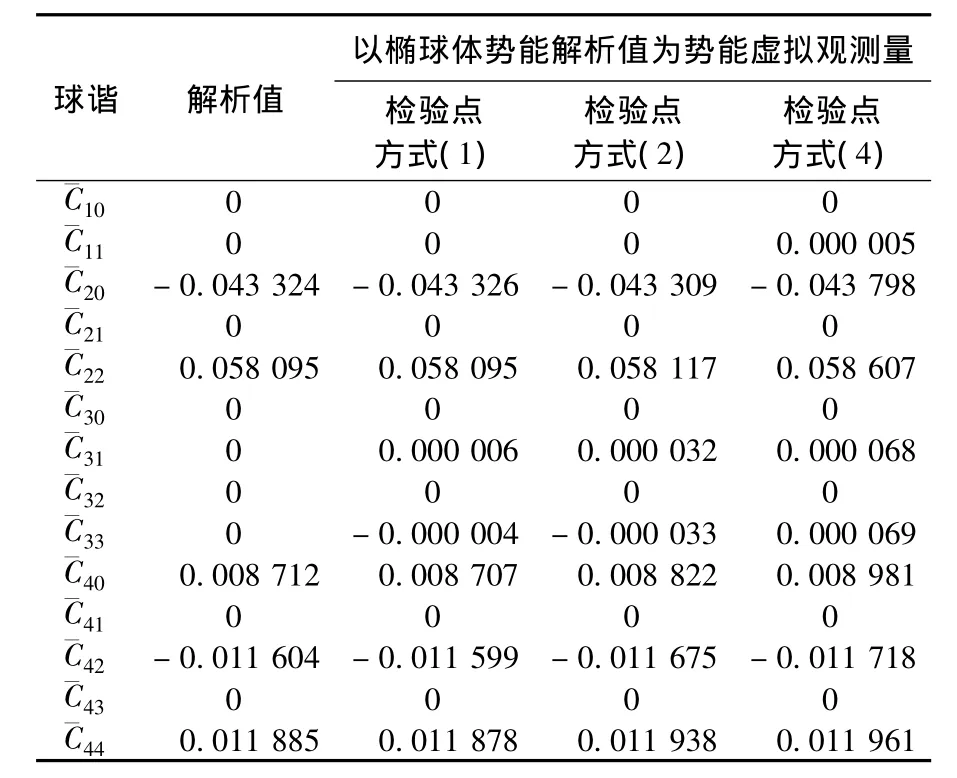
表4 球谐系数计算结果

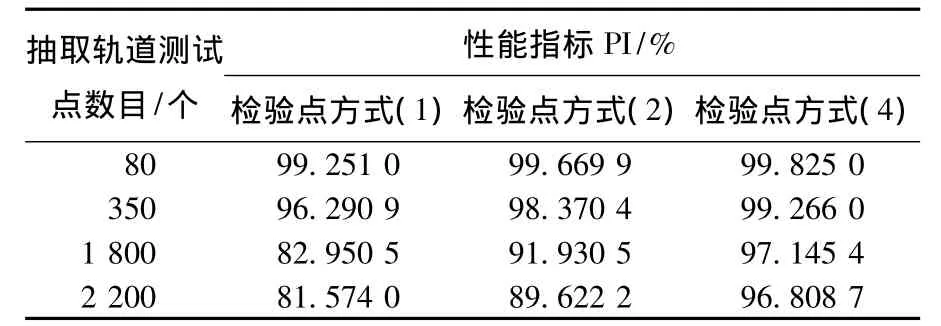
表5 椭球体北极盘旋轨道PI计算结果

由表 4、5结果知，检验点方式(1)、(2)到(4)，检验点逐步集中于椭球体北极，球谐系数与真实值的偏差增大，但对该活动区域的重力场建模精度显著提高.随着测试点的增多，局部球谐系数模型建模偏差积累效应明显比全局球谐模型小的多.针对局部活动区域得到的局部球谐系数模型对该区域的重力场建模精度可以大大提高.

3.2 布里渊球域内局部球谐系数

假设探测器需要在图7所示的近小行星区域进行低轨绕飞以获得到高精度观测数据，高度为10 km，处于布里渊球域内.

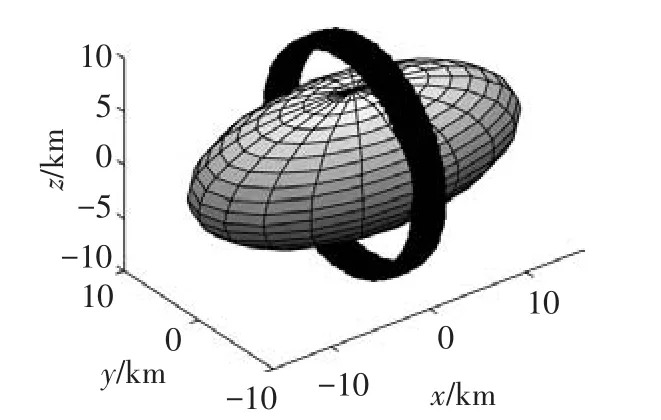
图7 探测器局部活动区域

集中在图7所示的局部活动区域内选取均匀分布形式的检验点，共计700个.求取球谐系数，见表6.选用图8所示的绕飞轨道进行验证.分别利用上述局部球谐系数和由检验点方式(1)得到的全球球谐系数对轨道抽取的测试点计算PI，结果见表7.由结果可知，局部球谐系数模型仍有极高的重力场拟合程度，而全球球谐系数已经发散，无法在该区域使用.

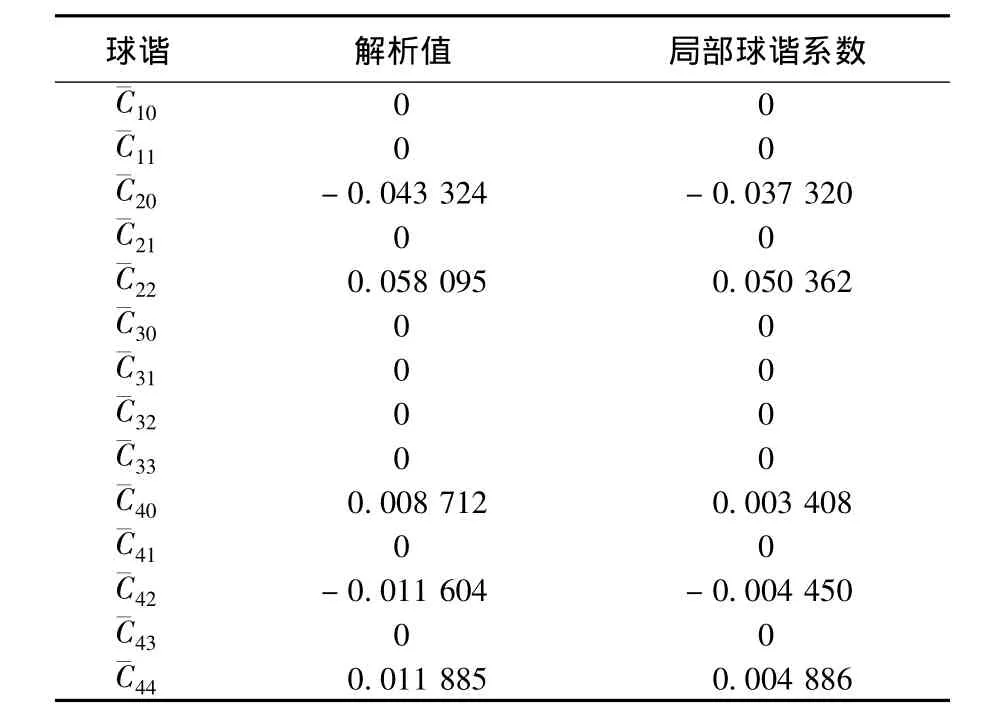
表6 局部球谐系数计算结果

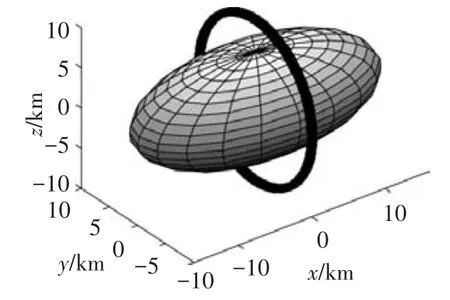
图8 探测器绕飞轨道

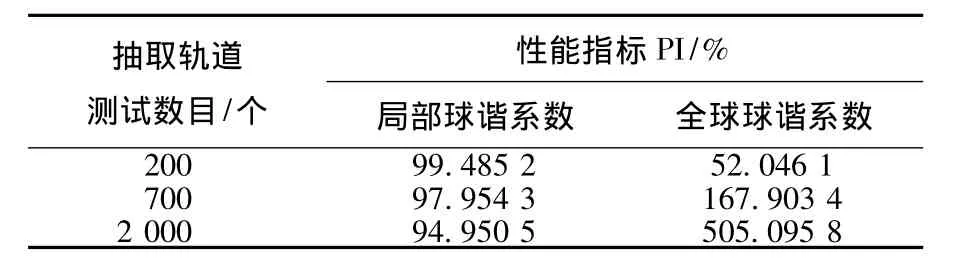
表7 椭球体统飞轨道PⅠ计算结果

4 小行星Eros球谐系数的求取

Eros433小行星于1989年发现，美国国家航空航天局(NASA)的NEAR-Shoemaker探测器对其进行了探测.据NASA公布，其质量(6.690 4±0.003)×1015kg，体积 2 503 ±25 km3，平均密度2.67 ±0.000 3 g·cm-3，大小34.4 ×11.2 ×11.2 km，均匀多面体模型如图9所示［15］.

图9 Eros多面体模型

4.1 全球球谐系数结果

利用本文方法求解其前15阶全球球谐系数，结果见表8.将结果与传统的三轴椭球体法和NEAR-Shoemaker实际环绕探测解算出的球谐系数相比较.计算过程中采用面数N分别为49 152和196 608的两种Eros均匀多面体模型.

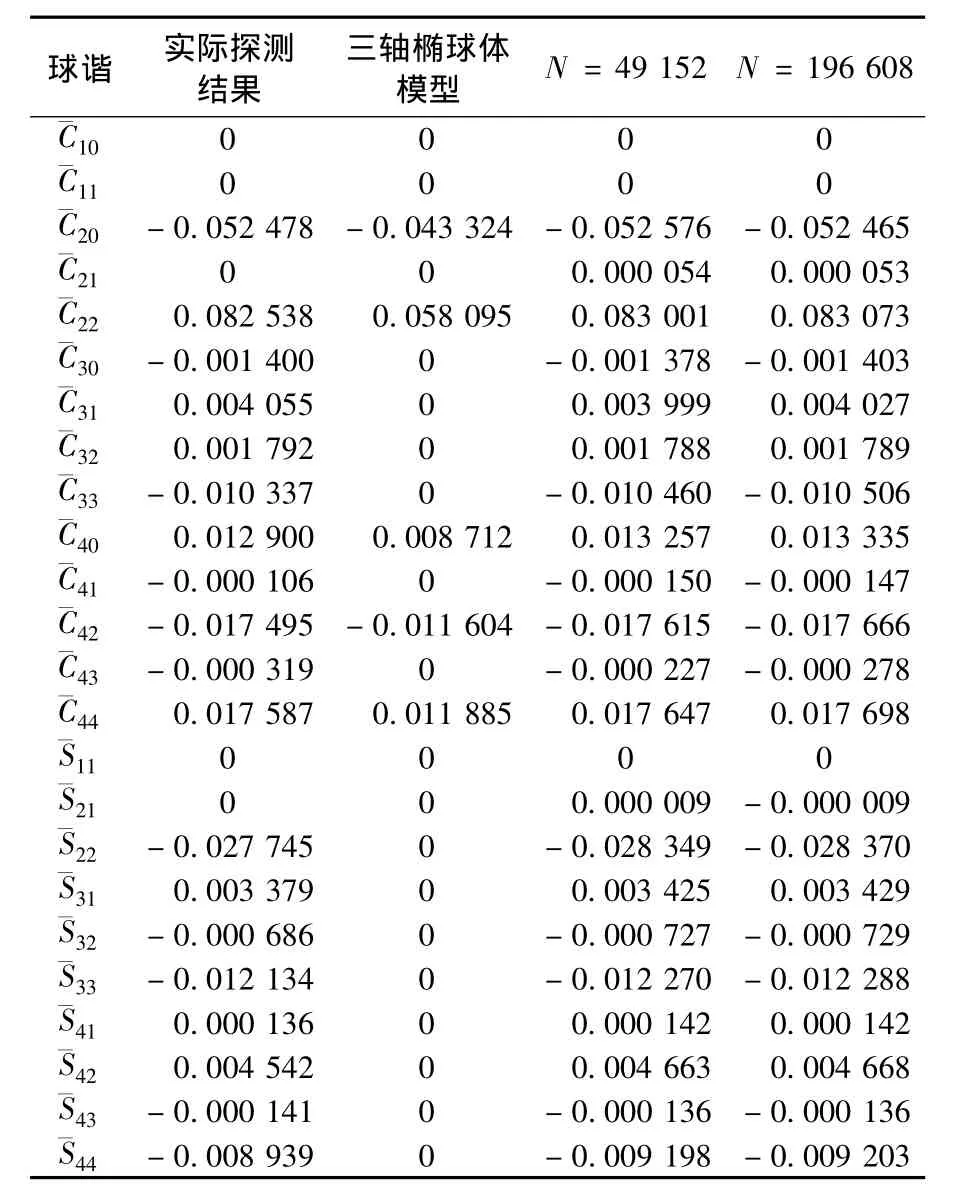
表8 Eros球皆系数求取结果

4.2 局部球谐系数结果

以探测器活动在高度为25 km的Eros北极上空为例，利用图3检验点方式(1)、(2)、(4)，基于Eros多面体模型求解球谐系数，并选取图6所示的轨道进行验证，计算PI，结果见表9.可见，对不规则形状小行星，由探测器局部活动区域得到的局部球谐系数相比全球球谐系数对该区域的重力场拟合程度更高.

以探测器活动在图7所示的局部区域为例，集中在此区域选取检验点，基于Eros多面体模型计算局部球谐系数，利用图3检验点方式(1)求取其全球球谐系数，并选择图8所示的绕飞轨道进行验证，计算PI，结果见表10.可见，基于局部球谐系数的球谐函数法在布里渊球域内针对该局部活动区域仍能保证较高的重力场建模精度.

表9 Eros北极盘旋轨道PI计算结果

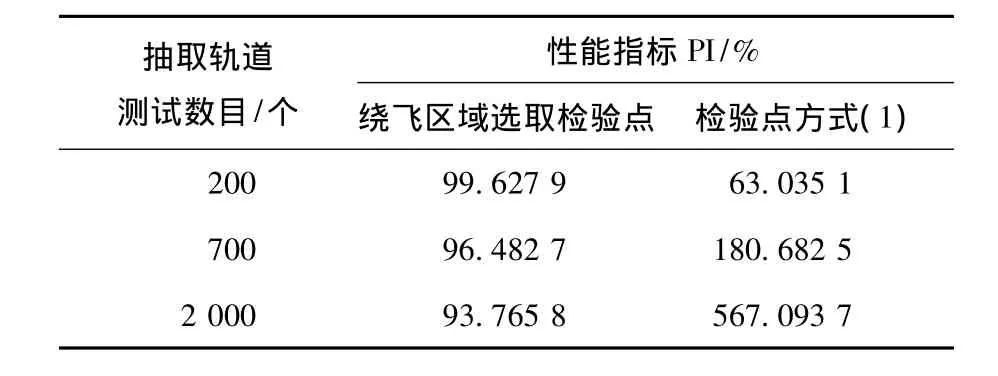
表10 Eros绕飞轨道PI计算结果

5 结语

本文讨论了小行星球重力场球谐系数计算相关问题.通过定性讨论和定量分析，结果表明均匀多面体模型和均匀分布的检验点保证了高精度的全球球谐系数的获得.针对探测器在某一特定区域活动情况，提出局部球谐系数概念，提高了局部区域重力场建模精度，扩展了球谐函数法的应用范围.

重力场模型提供分析、描述和设计地球表面及其外空间一切物体力学行为的先验重力场约束.精细的重力场信息为小行星探测任务的成功提供保障.而到目前为止，小行星重力场描述虽然众多，但都存在一定缺陷.因此，寻找一种以动态观、整体论的方法描述的具有普适意义重力场模型，更加直观地解释分析小行星重力场特性，具有一定的必要性和紧迫性，也将成为未来小行星探测的一大挑战.

［1］ZUBER M T，SMITH D E，CHENG A F，et al.The shape of 433 Eros from the NEAR-Shoemaker laser rangefinder［J］.Science，2000，289(5487):2097-2101.

［2］ BROSCHART S B，SCHEERES D J.Control of hovering spacecraft near small bodies:application to asteroid 25143 Itokawa ［J］.Journal of Guidance，Control，and Dynamics，2005，28(2):343-354.

［3］YANO H，KUBOTA T，MIYAMOTO H，et al.Touchdown of the hayabusa spacecraft at the Muses Sea on Itokawa［J］.Science，2006，312(5778):1350-1353.

［4］徐伟彪，赵海斌.小行星深空探测的科学意义和展望［J］.地球科学进展，2005，20(11):1183-1190.

［5］CASTOTTO S，MUSOTTO S.Methods for computing the potential of an irregular，homogeneous，solid body and its gradient［J］.AIAA Paper，2000，4023:82-96.

［6］KAULA W M.Theory of Satellite Geodesy:Applications ofSatellitesto Geodesy［M］. Mineola:Dover Publications，2000:4-8.

［7］WERNER R A，SCHEERES D J.Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representationsofasteroid 4769 castalia［J］. CelestialMechanicsand Dynamical Astronomy，1997，65(3):313-344.

［8］ PARK R S， WERNER R A， BHASKARAN S.Estimating small-body gravity field from shape model and navigation data［J］.Journal of Guidance，Control，and Dynamics，2010，33(1):212-221.

［9］ SCHEERES D J.Dynamics about uniformly rotating triaxial ellipsoids:applications to asteroids［J］.Icarus，1994，110(2):225-238.

［10］HU W，SCHEERES D J.Numerical determination of stability regions for orbital motion in uniformly rotating second degree and order gravity fields［J］.Planetary and Space Science，2004，52(8):685-692.

［11］SCHEERES D J.Orbit mechanics about asteroids and comets［J］. JournalofGuidance Controland Dynamics，2012，35(3):987.

［12］张振江，崔祜涛，任高峰.不规则形状小行星引力环境建模及球谐系数求取方法［J］.航天器环境工程，2010，27(3):383-388.

［13］宁津生.地球重力场模型及其应用［J］.冶金测绘，1994，3(2):2-6.

［14］LI J C，CHAO D B，NING J S.Spherical cap harmonic expansion for local gravity-field representation ［J］.Manuscripta geodaetica，1995，20(4):265-277.

［15］National Aeronautics and Space Administration.http://sbn.psi.edu/pds/resource/rshape.html.2010-4-20.