考虑安装错位的弧齿锥齿轮小轮齿面再设计

蔡香伟，方宗德，候祥颖

(西北工业大学机电学院，710072西安)

弧齿锥齿轮因具有传动平稳、承载能力强等优点，被广泛应用于航空、车辆及机床的动力系统中.传动过程中两相互啮合的轮齿形成的齿面印痕与齿轮的强度和振动特性密切相关，是传动性能的重要指标.实际工况下，减速器中的箱体、轴承、轴系和齿轮的变形，安装误差、制造误差和随机误差的存在，以及温度、振动等因素的影响，齿面印痕将偏离理想位置(反映为齿轮副的当量安装错位［1］)，这一直是齿轮设计和使用中的重要问题.由于弧齿锥齿轮齿面几何结构复杂，支撑变形也非常复杂，精确地计算和测量十分困难.工程中历来采用经验的方法或多次试加工和调整的方法，所需周期长，效果并不理想［2］.因此，根据齿面印痕的偏移，识别相应的当量安装错位(以下简称安装错位)，将其反馈到齿面再设计中，对于提高齿轮副实际工况下的啮合质量具有重要的工程意义.

国内外学者就安装错位与齿轮副啮合特性(接触印痕和传动误差)的相互关系进行了大量研究.Litvin 等［3］、Simon［4-5］、汪中厚等［6］分析了安装错位作用下齿面印痕的变化;唐进元等［7］综合分析了机床运动误差和安装错位对齿面接触质量的影响;吴训成等［8］用完全解析的方法分析了点接触齿面的接触点位置对安装错位的敏感性问题;苏进展等［9-11］通过齿面修形、差曲面的全曲率优化、印痕敏感性系数的优化等方法改善了弧齿锥齿轮的安装错位敏感性;唐进元等［12-13］考虑初始计算点位置对安装错位敏感性的影响，对预定传动误差曲线的弧齿锥齿轮齿面设计方法进行了改进，降低了安装错位的敏感性;而对于安装错位的识别及错位下的齿面再设计问题，相关研究较少，仅见文献［14］通过载荷变化与印痕移动的近似线性关系计算错位值，并采用基于齿面印痕和传动误差的齿面主动设计方法重新设计齿面几何.由于多种安装错位的组合可能引起相同的印痕偏移，即这一问题存在多解性，但该文献中并未对其进行有效说明.

本文主要研究基于齿面印痕偏移的安装错位识别及错位下的齿面再设计问题.建立了考虑安装错位的弧齿锥齿轮几何接触分析模型，分析了不同错位组合之间的内部联系，说明多解性的产生机理;提取齿面印痕的数值特征，以逼近接触轨迹曲线为优化目标，识别与齿面印痕相匹配的当量安装错位;在局部综合法的基础上，根据当量安装错位重新设计小轮的齿面几何，使齿轮副在实际的安装错位条件下仍具有较好的啮合性能.

1 安装错位与齿面印痕

根据GB11365—1989的规定，弧齿锥齿轮副在实际的安装中，需要考虑的错位因素主要有小轮齿圈轴向位移P、大轮齿圈轴向位移G、齿轮副的轴间距E与轴夹角Σ，如图1所示.

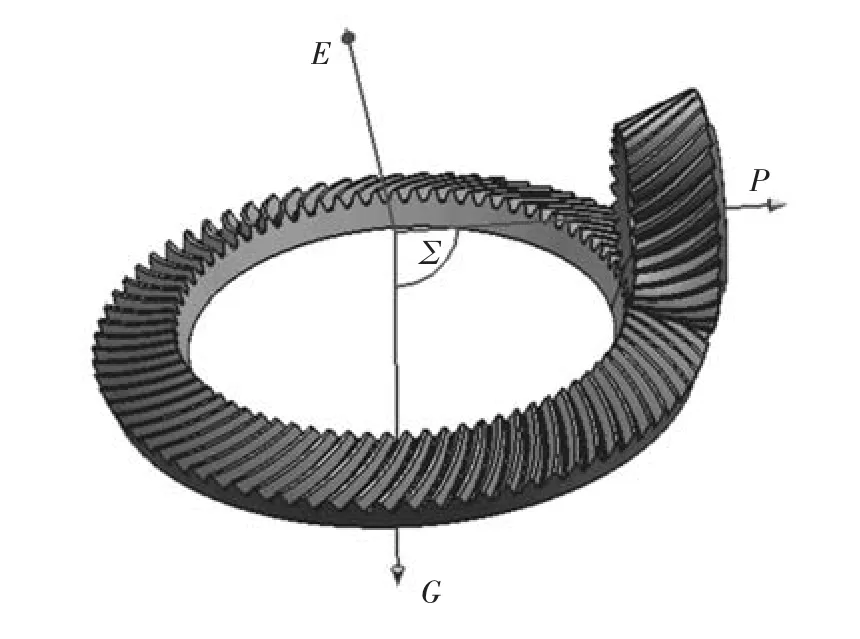
图1 弧齿锥齿轮副的安装错位

1.1 啮合坐标变换与几何接触分析

由图1建立弧齿锥齿轮副的啮合坐标系如图2所示.坐标系S1和S2分别刚性连接在小轮与大轮上，Sh为固定参考坐标系，添加辅助坐标系Sc1以描述安装中的错位，φ1与φ2是小轮与大轮的啮合转角.图中各错位正方向规定如下:小轮轴向错位ΔP为‘+’时移向小轮大端;大轮轴向错位ΔG为‘+’时移向大轮大端;轴间距错位ΔE为‘+’时小轮轴线在大轮轴线下方;轴交角错位ΔΣ为‘+’时轴交角增大.

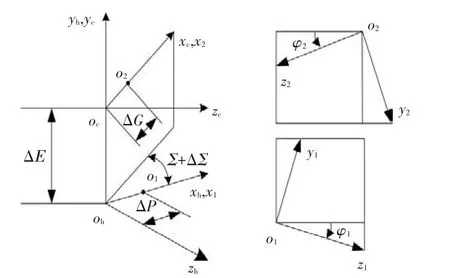
图2 齿轮啮合数学模型

将小轮与大轮的齿面位矢及法矢分别表示在坐标系Sh中:

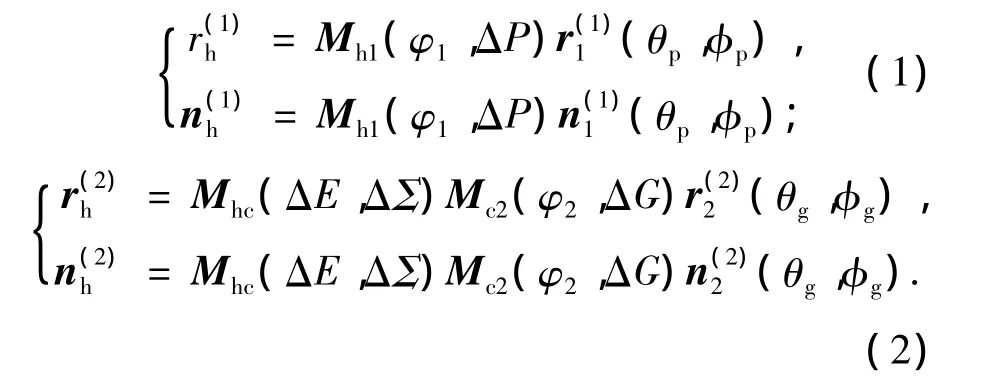
式中:ξi=［θi，φi］(i=p，g)是齿面参数，小轮与大轮的位矢及法矢具体表达式可参考文献［15］;φ1、φ2为小轮与大轮的啮合转角;Mh1、Mc2、Mhc分别是坐标系S1到Sh、S2到Sc、Sc到Sh的齐次变换矩阵，如下所示:

小轮与大轮齿面在固定坐标系Sh中连续相切接触，得到轮齿接触分析(TCA)基本方程为

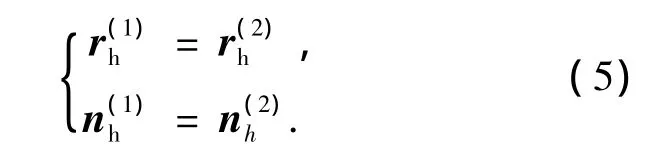
错位向量D= [ΔP，ΔG，ΔE，ΔΣ]已知，由于，式(5)只有5个独立的标量方程，未知量有6个，取小轮啮合转角φ1为输入量，可得齿面上的一个接触点，然后以一定步长改变φ1，继续求解，直至求出的接触点超出齿面的有效边界，即可得到齿面的接触轨迹.在啮合点处，由齿面参数确定两齿面的相对曲率，结合齿面的弹性变形量不大于0.006 35 mm，计算该点处的接触椭圆，而齿面印痕就是由一系列的接触椭圆组成的.

1.2 错位多解性分析

由式(1)、(2)可知，小轮、大轮齿面上的点在固定坐标系中的位置是由齿面参数ξi、安装错位D及各自的啮合转角φ1、φ2确定的，齿面上任意两点的相对位矢

不同的错位组合作用下，啮合的每一瞬时两齿轮在固定坐标系Sh中的绝对坐标是不同的，但相对坐标如果相同，即小轮与大轮齿面上任意两点的相对位矢Δr一致，存在唯一的“空间等效向量”，则齿轮副的啮合状态是等价的，这将产生相同的齿面印痕.

由于“空间等效向量”的唯一性，在进行错位识别时，只需根据实际齿面印痕的偏移确定一组满足“空间等效向量”的当量错位即可，无需精确计算出真实的错位，错位的识别由寻找“真解”转换为寻找“等效解”，避免了从结构、受力等方面分析产生印痕偏移的原因，大大降低了问题的研究难度.

2 安装错位识别

2.1 齿面印痕的数值描述

实际齿面印痕的物理资源为印痕拓片或照片，必须提取其数值特征，才能进行后续处理.图3为齿面印痕参数化示意图，数值特征包括印痕中心坐标、印痕面积、印痕方向角.其中印痕方向角为接触轨迹曲线上进入啮合点与退出啮合点连线与节锥的夹角.从图中可以看出，中心点坐标代表齿面印痕的整体位置，印痕面积反映了轮齿的承载情况，印痕方向角表示啮合点在齿面的运动方向.

图3 齿面印痕参数化表示

2.2 优化模型

有效的算法是保证错位识别精度的关键因素.由于齿面接触轨迹代表了轮齿从进入啮合到退出啮合的完整过程，这里通过对接触轨迹曲线的控制，可以实现高精度的错位识别.

给定一组安装错位D，由几何啮合仿真得到齿面上的接触点拟合的接触轨迹曲线记为ld，ld上离散点的位置矢量与法线矢量分别表示为

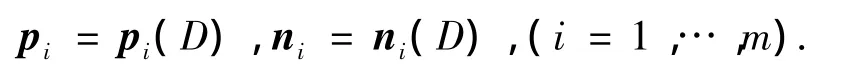
其中m为离散点的数目.

由实际齿面印痕拟合的接触轨迹曲线记为lt，lt与ld的偏差如图4所示，优化的目标是寻求一组安装错位，使得ld逼近于lt.

图4 接触轨迹偏差示意图

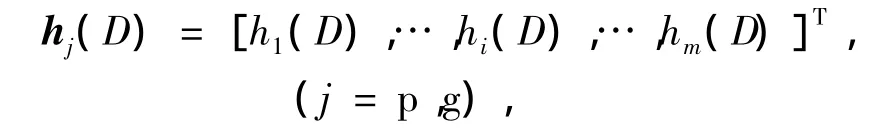
则lt上的离散点可表示如下:

将式(6)代入lt的曲线方程中，求解非线性方程即可计算当前离散点的偏差hi.

以两曲线偏差的平方和最小为目标，建立最小二乘法目标函数模型:

3 安装错位下的齿面再设计

对于识别的安装错位D= ［ΔP，ΔG，ΔE，ΔΣ］，主要应用是将其引入到弧齿锥齿轮小轮齿面的再设计中，通过调整机床参数改变齿面的微观几何，使齿轮副在错位条件下的啮合印痕仍能处于理想的位置.本文在局部综合法［15］的基础上，考虑安装错位的影响，重新设计小轮机床参数.在进行局部综合时，大轮参考点的位矢、法矢及主方向由动坐标系S2到固定坐标系Sh的坐标变换矩阵如式(3)、(4)所示，由固定坐标系Sh到动坐标系S1的坐标变换矩阵为

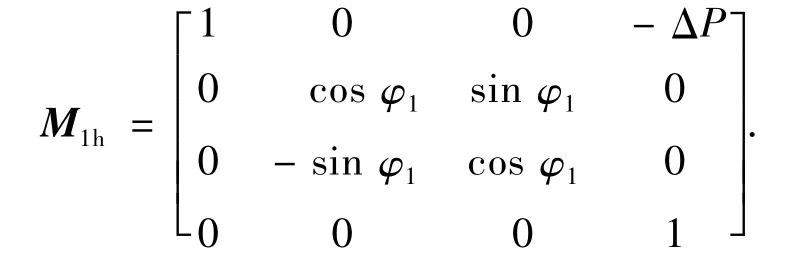
经过以上变换，预置参考点的二阶接触参数:传动比函数的一阶导数m'21、接触轨迹曲线的切线方向η2、接触椭圆长半轴长度a等，根据局部综合法相关公式，即可计算小轮的加工参数.

4 算例

以一对弧齿锥齿轮(大轮展成法加工，小轮变性法加工)为例，验证本文方法.轮坯设计参数见表1，假定大轮凸面与小轮凹面啮合，表2为大轮的机床参数，表3为原始设计的小轮机床参数.

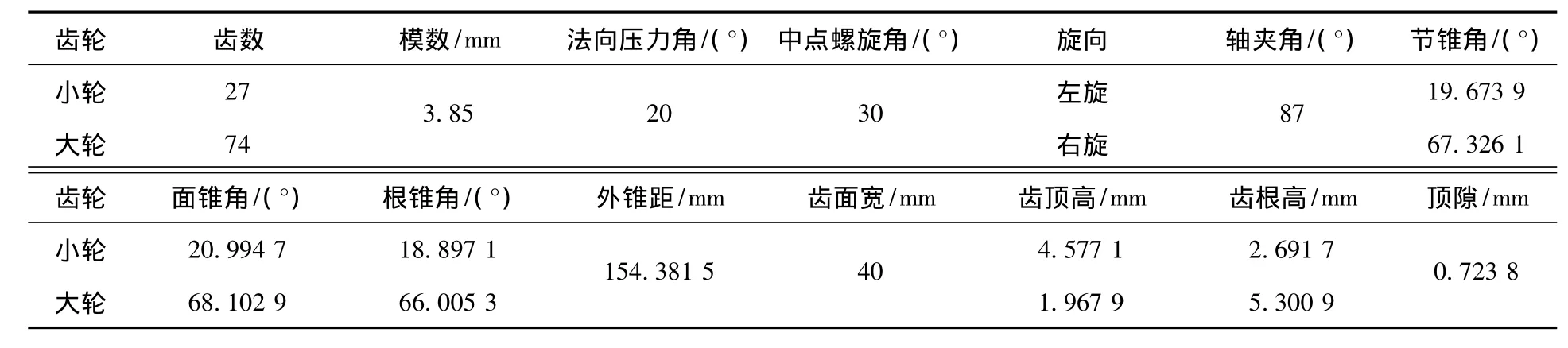
表1 轮坯设计参数

表2 大轮机床参数

表3 小轮原始设计机床参数

齿轮副的标准安装位置为D0，在本文的仿真中作为方法验证，人为拟定错位量Dt作为实际错位(安装错位的真值)，以大轮的轴向位移分量ΔG作为不变量，给定初值为-0.05 mm，优化得到一组当量安装错位De.三组错位的分量见表4.

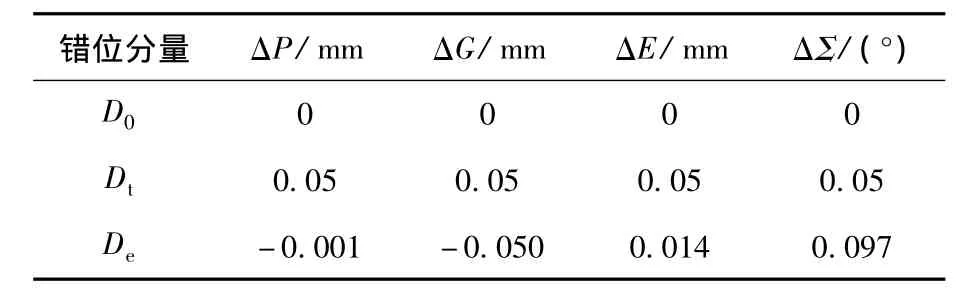
表4 安装错位数值

绘制齿轮副在三组错位下的接触印痕及传动误差如图5、6所示.

通过以上计算可知，对于原始设计的齿轮副，标准安装位置的齿面印痕位于齿宽中部，接触轨迹曲线呈一定角度的倾斜，设计重合度为2.5，传动误差曲线啮合转换点幅值为8″;在实际错位下，齿面印痕的形状改变不大，但印痕中心位置移动明显，齿面印痕向小端偏移，印痕的面积也有一定程度的减小;当量错位下的齿面印痕，其大小、方向、位置均与实际错位下的齿面印痕非常接近，说明错位的识别取得了较高的求解精度.

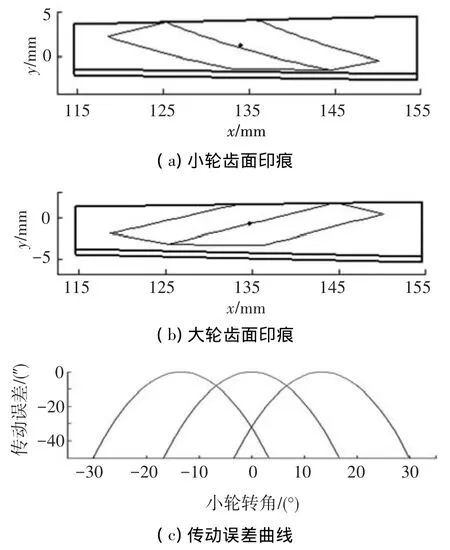
图5 标准安装位置D0的TCA结果

图6 实际错位Dt与当量错位De的TCA结果

表5中序列1～3分别是D0、Dt、De作用下齿面印痕的数值特征.分别基于实际错位Dt与当量错位De进行小轮齿面的重新设计(预置参数m'21、a保持不变，微调η2保证齿轮副的设计重合度，微调大轮参考点在齿高方向的位置保证传动误差曲线的对称性)，得到小轮机床参数记为Mp-Dt、Mp-De，相关数值见表 6，两再设计齿面的偏差如图7所示.

局部综合法通过模拟大轮与小轮在参考点处的啮合确定小轮机床参数，两组安装错位下齿轮副在啮合固定坐标系中的绝对位置不同，这导致了再设计的小轮齿面具有不同的机床参数，如表6;但齿轮副的相对位置基本相同，决定了在大轮齿面点全相同的前提下小轮齿面的微观几何也基本一致，如图7所示，齿面偏差的最大值为1μm.理论上，对于完全等效的不同安装错位组合，采用同种方法再设计小轮机床参数后将得到相同的齿面几何结构，因此，对于工况下的齿面再设计问题，无需精确计算出真实的安装错位.实际应用中，再设计齿面的偏差大小取决于错位识别的精度，而文中所述错位识别算法可以满足工程应用的需要.

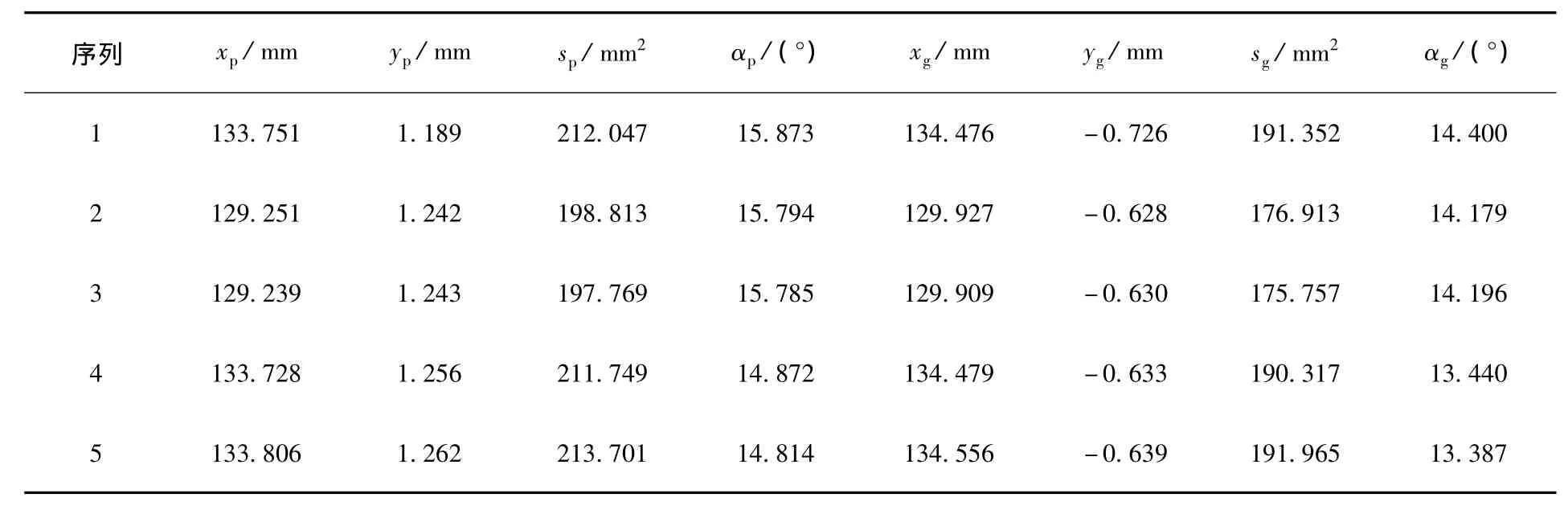
表5 印痕的数值特征

图7 机床参数Mp－De与Mp－Dt的齿面偏差

将Mp-Dt与Mp-De分别在实际安装错位Dt下与大轮啮合，设计重合度为 2.500、2.506，齿面印痕与传动误差如图8所示，印痕的数值特征见表5中序列4～5，与标准安装的原始设计相比，齿轮副的啮合状态基本相同，基于当量安装错位的齿面再设计取得了良好的效果.

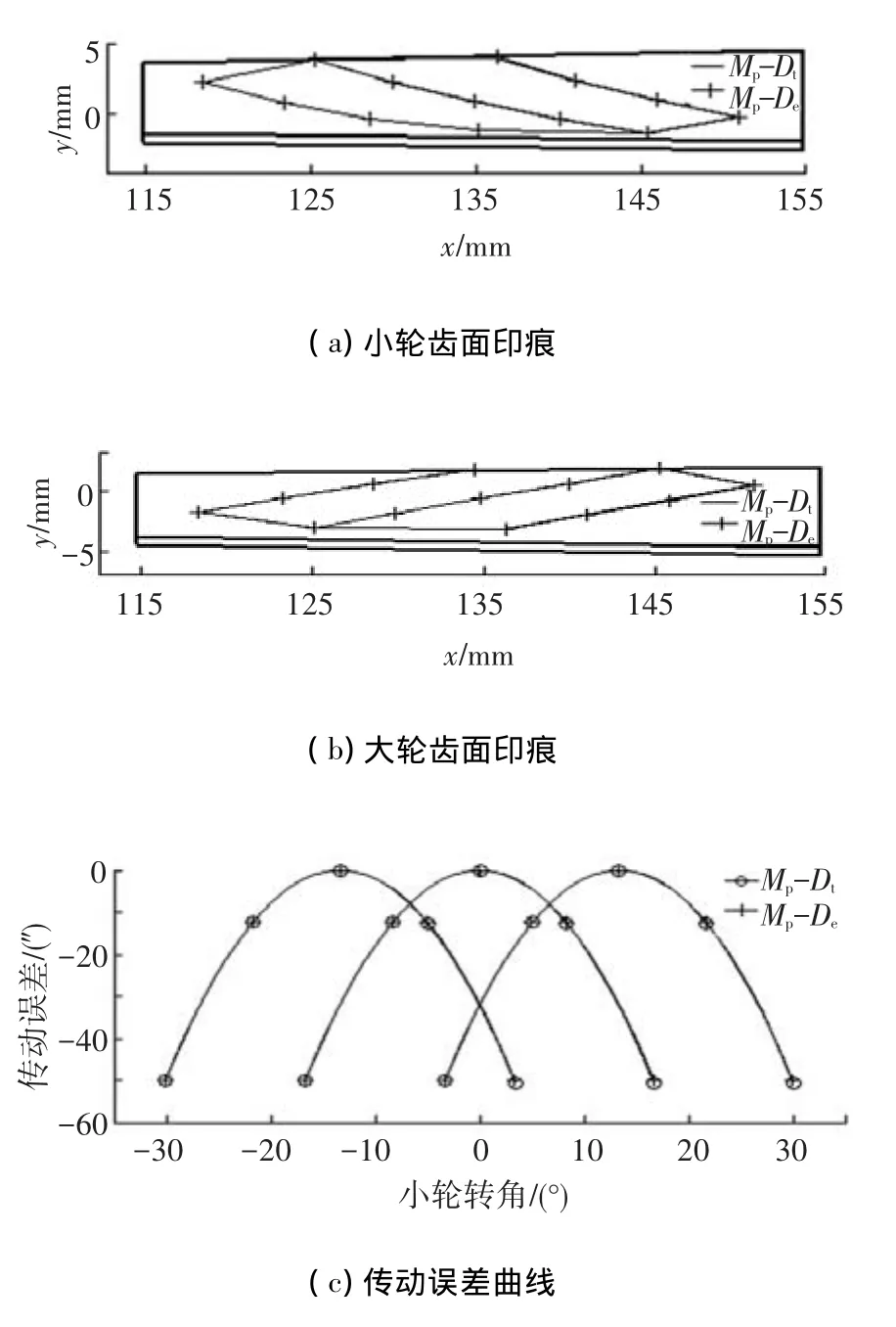
图8 再设计齿面在实际错位Dt下的TCA结果

5 结论

1)不同的安装错位可以导致相同的齿面印痕，但这些错位组合之间存在等价关系，安装错位的识别问题由确定真解转换为计算一组等效解.

2)对于完全等效的两组安装错位，在同样的方法下进行小轮齿面的再设计，将得到不同的机床参数，但这些机床参数加工的小轮齿面具有相同的几何拓扑结构.

3)提取齿面印痕的数字化特征，以逼近齿面接触迹线为目标，通过优化方法可以高精度地识别与齿面印痕匹配的当量安装错位.

4)以一对弧齿锥齿轮副为例，基于局部综合法，分别在实际安装错位与当量安装错位下重新设计小轮齿面，通过比较小轮再设计齿面的差曲面，结合在实际安装错位下的几何接触分析，验证了文中所述方法的正确性.

［1］SIMON V.Optimal machine tool setting for hypoid gear improving load distribution ［J］.ASME Journal of Mechanical Design，2001，123(12):577-582.

［2］齿轮手册编委会.齿轮手册［M］.北京:机械工业出版社，2000.

［3］LITVIN F L，CHEN J.Computerized simulation of transmission errors and shift of bearing contact for face-milled hypoid gear drive［J］.ASME Journal of Mechanical Design，1995，117(6):262-268.

［4］SIMON V.Computer simulation of tooth contact analysis of mismatched spiral bevel gears［J］.Mechanism and Machine Theory，2007，42:365-381.

［5］SIMON V.Influence of tooth errors and misalignments on tooth contact in spiral bevel gears［J］.Mechanism and Machine Theory，2008，43:1253-1267.

［6］汪中厚，余剑，张兴林.安装误差对弧齿锥齿轮齿面接触轨迹影响的分析研究［J］.机械传动，2014，38(2):21-24.

［7］唐进元，卢延峰，周超.有误差的螺旋锥齿轮传动接触分析［J］.机械工程学报，2008，44(7):16-23.

［8］吴训成，毛世民，吴序堂.点接触齿面的安装误差敏感性研究［J］.中国机械工程，2000，11(6):700-703.

［9］苏进展，方宗德.弧齿锥齿轮低敏感性修形［J］.航空动力学报，2012，27(8):1895-1901.

［10］苏进展，方宗德.弧齿锥齿轮误差敏感性优化设计［J］.航空动力学报，2012，27(11):183-189.

［11］苏进展，方宗德.弧齿锥齿轮印痕稳定性优化设计与试验［J］.航空动力学报，2012，27(11):2622-2628.

［12］唐进元，雷国伟，杜晋，等.螺旋锥齿轮安装误差敏感性与容差性研究［J］.航空动力学报，2009，24(8):1878-1885.

［13］唐进元，杜晋.考虑安装误差敏感性的螺旋锥齿轮主动设计方法［J］.中国机械工程，2009，20(10):1197-1201.

［14］方宗德，曹雪梅，张金良.航空弧齿锥齿轮实际工况下的当量错位反求及齿面再设计［J］.中国机械工程，2007，18(24):3001-3005.

［15］LITVIN F L，FUIENTES A.Gear geometry and applied theory［M］.New York:Cambridge University Press，2004.