未知故障下的飞机自适应控制

王常虹，钟佳朋，伊国兴，李清华，奚伯齐

(哈尔滨工业大学空间控制与惯性技术研究中心，150001哈尔滨)

飞行安全一直是研究人员十分关注的问题，每年因飞机故障失控等都会带来巨大的损失.近年来，研究人员对故障状态下的飞行控制已经进行了比较深入的研究.故障状态下的飞机控制是一个十分复杂的问题，例如控制舵面故障可能会影响飞机的机动性能，同时需要非常规的控制策略［1-2］，尽管可预测和可判断的故障可以通过提前预设的控制方案来补偿，但是遇到未知情况下不可预测的故障时则需要控制参数的自适应改变来控制飞机的状态.本文主要研究大型飞机动力学模型在不可预测以及未知故障情况下的飞行控制.主要考虑机体结冰以及控制舵面卡死两种情况.对于机体结冰，文献［3］给出了飞机在结冰情况下的动力学改变情况，主要体现在:1)飞机的升力系数减小;2)零界攻角减小;3)阻力系数增大;4)失速速度增大.通过飞行试验表明［4-5］:一般情况下，飞机在结冰时升力系数减小约5% ～15%，同时阻力系数增加约15% ～50%.机体结冰时，飞机无法保持原来的系统状态，需要相应的调整引擎及控制舵面的输出来调节飞机的姿态与速度保持平稳飞行.

当飞机控制舵面卡死时，如果不能及时保持飞机稳定，极易造成飞机坠毁等严重后果.对于大型飞机，主控制输入主要包括左右引擎、升降舵偏、副翼舵偏以及方向舵偏，当某一个舵面发生故障时，理想情况是通过其他控制输入在功能上的冗余来补偿当前舵面的故障，从而保持飞机当前的平稳飞行状态.在极端情况下，当前飞行状态由于某一舵面故障而成为不稳定且不可控的状态时，要求飞机能够迅速的自适应地达到状态空间上的临近平稳飞行状态.

飞机在实际飞行出现故障时，飞行辅助系统需要一定时间通过在线故障诊断方法或者在线系统辨识方法来定位故障或者辨识发生改变的系统模型.在此之前，飞机的故障是未知的，这就需要控制器能够在未知的故障状态下根据系统输出和状态来自适应的迅速调节控制器增益来保证飞机的平稳飞行.

张爱华等［6］针对航天器执行机构安装偏差及外部干扰提出一种自适应补偿控制策略.Rysdyk等［7］提出一种神经网络控制系统结构，利用逆动态模型实现了飞机的直接自适应控制.Kaneshige等［8］针对商用大型飞机进行大量的仿真，证明了在一定的条件下基于神经网络的飞行控制系统能够对特定的故障进行辨识和定位.Nguyen等［9］提出一种用于保持故障飞机稳定性的直接-间接自适应飞行控制器.Page等［10］对已有的自适应控制规律进行改进并将其应用于F/A-18C飞机上对其进行验证.

传统的比例积分微分(PID)控制方法在飞机系统出现故障时，无法自适应的调整控制器参数及时保证飞机稳定.本文将基于回顾成本的自适应控制方法(retrospective cost adaptive control，RCAC)运用于大型飞机机体结冰和控制舵面卡死两种情况，并对其进行研究.RCAC方法是基于系统输出反馈的自适应控制方法，具有很好的鲁棒性，可以利用较少的系统信息来达到控制目的.文献［11-12］介绍了RCAC算法的基本思想，文献［13-16］介绍了RCAC在飞行器控制等方面的一些应用.相对PID方法，RCAC可以实时的根据飞机系统变化来自适应的调整控制器增益，在飞机系统出现故障时能够迅速的达到稳定飞行目标，同时为系统后续的实时故障诊断以及飞行包络线分析提供保证.NASA-GTM模型是一种通用的双引擎大型飞机模型，模型中的各个动力学系数是通过数值分析与风洞试验获得.这些参数数据被存储成为一些列可查数据库提供给研究人员进行模拟仿真与控制算法设计等研究.本文在完整的非线性NASA-GTM模型上进行仿真，通过调整模型来模拟机体结冰和控制舵面卡死的情况.由于在NASA-GTM这种复杂非线性系统中，舵面卡死或者气动参数变化会产生很大的不确定性，其他的控制器很难解决这种情况，本文采用的RCAC控制方法经过仿真验证可以很好地达到控制效果.

1 自适应控制器设计

1.1 问题提出

将非线性飞机模型在某一平衡点线性化然后离散化得到如下多输入多输出系统:

其中x(k)∈Rn，y(k)∈Rly，z(k)∈Rlz，u(k)∈Rlu，w(k)∈Rlw，k≥0.本文目的是设计一个自适应输出反馈控制器在激励信号w作用下运用尽量少的模型信息使性能指标z最小化.w既可以代表需要执行指令信号，也可以代表需要抑制外部干扰信号.方程(1)～(3)可表示为通过对连续系统采样并保持后得到的一个离散系统.如果D1=0、E0≠0，则控制目标是让输出E1x跟踪指令信号-E0w.如果D1≠0、E0=0，则控制目标是在抑制干扰w.进一步分析，如果D1=［10］，E0=［00］，同时w(k)=［w1(k)Tw2(k)T］T，则控制目标是让输出E1x跟踪指令信号0w2同时抑制干扰w1.最后，如果D1和E0是零矩阵，则系统目标输出稳定，使z收敛至零.

1.2 回顾成本定义

首先定义系统的马尔可夫参数，当i≥1时，

取r为正整数，然后对于所有k≥r，

其中:

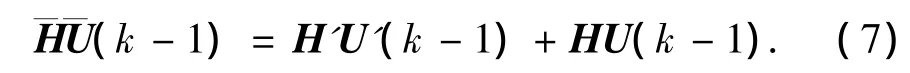
式中:H'∈Rlz×(rlu-lU)，H∈Rlz×lU，U'(k-1)∈Rrlu-lU，U(k-1)∈RlU.然后将方程(6)改写为

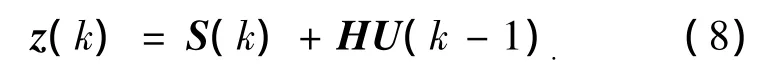
式中S(k)为系统中的未知部分，

接下来，引入一个延时kj(j=1，2，…，s)，且0≤k1≤k2≤…≤ks，方程(8)将改写为

方程(9)变为

方程(7)变为

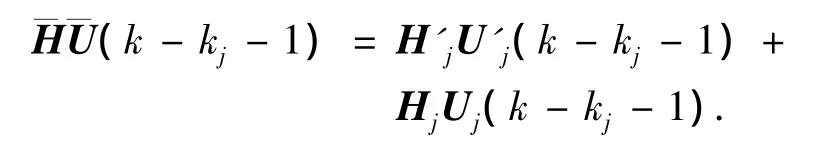
定义扩展性能变量:

由此可以得到

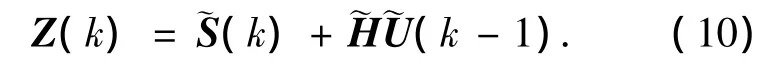
其中:根据(k-1)的排列决定.例如取s=2，k1=1和k2=2，则

下面定义回顾性能变量:

将真实的控制器输出Uj(k-kj-1)由一个重构的控制器输出U*j(k-kj-1)代替，然后得到扩展回顾性能变量为

将方程(10)代入方程(11)得到

最后定义回顾代价方程为

式中:R(k)∈Rslz×slz是一个正定的性能权重矩阵.本文目的是找到一个可以提供比Uj(k-kj-1)更好性能的重构的控制器输出U*j(k-kj-1);然后通过这个重构的控制器输出来更新控制器参数.

1.3 基于自适应调整的代价函数最优化

为了保证方程(13)具有一个全局最小值，将代价函数调整为

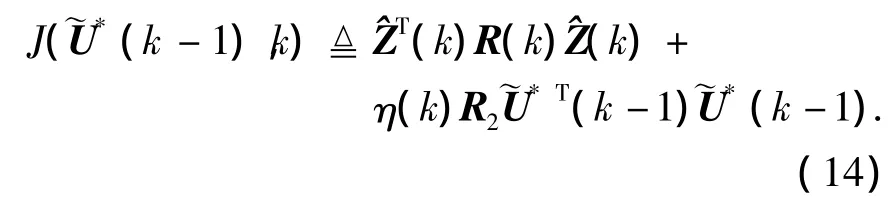
式中:η(k)=η0zT(k)z(k)，η0≥0.将方程(12)代入方程(14)得

式中:

当列满秩或者η(k)＞0时，AE(k)是可求逆的，这种情况下J(*(k-1)，k)具有唯一的全局最小解:

1.4 控制器结构

根据子系统阶数nc，子系统的输出u(k)可写为

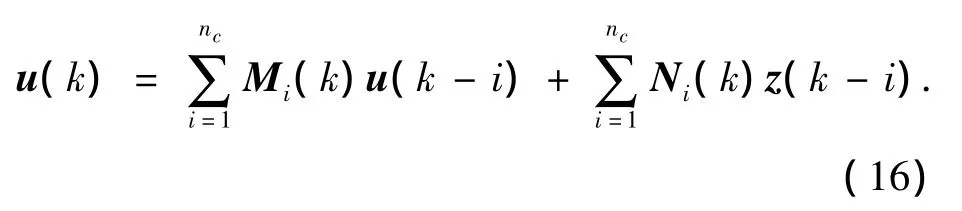
式中:Mi(k)∈Rlu×lu，Ni(k)∈Rlu×lz.控制器的输出式(16)可改写为

其中θ(k)包含控制器所有增益，且

1.5 最小二乘法更新控制器增益

采用递推最小二乘法，并利用φ(k-1)与方程(15)中重构的控制器输出*(k-1)来得到自适应控制器的增益.

取d＞0使*(k-1)包含u*(k-d)，然后选取最小二乘法的指标函数为

式中:φ(k-d)由方程(18)给出，‖·‖2为欧几里德范数，λ(k)∈(0，1］为遗忘因子.

根据最小二乘法的递推可以得到

其中

最终的RCAC控制输入为

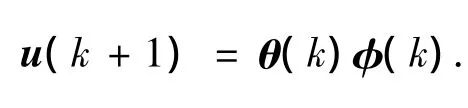
2 机体结冰情况下的自适应控制

本节通过近似模拟飞机机体结冰时的系统参数变化来进行飞机自适应控制研究.仿真目标是运用RCAC来进行空速、高度与航向角的控制，控制框图如图1所示.

图1 RCAC系统结构

图中r为飞机控制指令，包括了空速V、高度h与航向角ψ.仿真中，控制指令是为让系统输出y保持在系统动力学参数因外部原因而变化之前的状态.z代表3个控制命令与系统输出误差信号.RCAC 控制器输出信号包括δe、δa、δr、δLT与δRT，分别代表了升降舵舵偏、副翼舵偏、方向舵舵偏与左右引擎的输出.

基于图1中的控制结构进行仿真.其中的控制指令是要保持最初的平稳飞行高度，航向与空速.在t=500 s时，通过改变升力系数CL与阻力系数CD来近似模拟机体结冰时升力变小且同时阻力变大的状况.仿真中设定的两个系数变化情况为

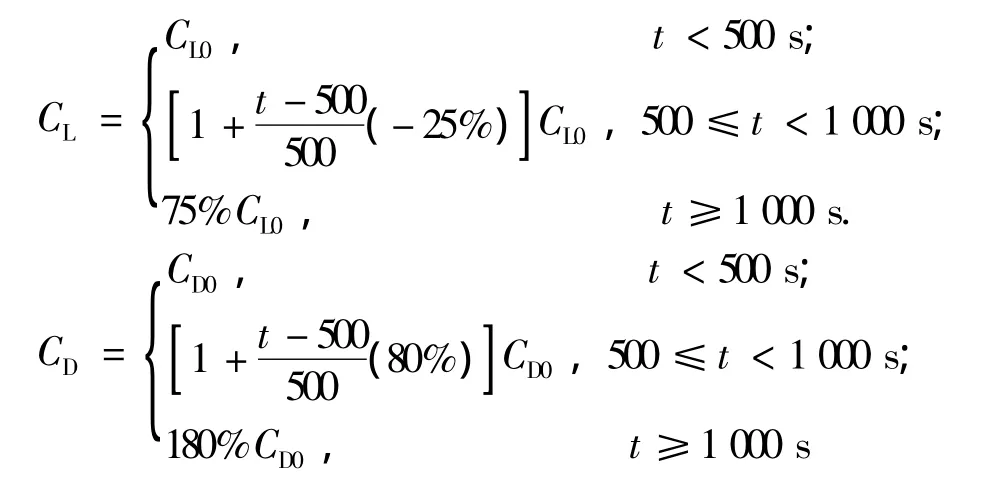
在t=500 s时，飞机的升力系数逐渐减小

25%，同时飞机的阻力系数逐渐增加80%.这里，

CL0与CD0代表当前状态下正常的升力系数与阻力系数，通过实时检索气动力系数数据库得到.

RCAC控制器参数配置为

式中马尔科夫变量H由GTM模型在平稳状态时线性化得到.

以上的控制器参数是根据系统的输入输出通过调试选取［11-13］.在本节中的算法设计中，先通过系统的输入输出以及状态参数得到当前状态的线性化近似模型，然后由该模型得到系统的马尔科夫参数H2和H3，RCAC算法可以只运用极少的系统信息(这里仅仅是H2和H3)来进行算法的设计.实际上，由于RCAC算法极强的鲁棒性，虽然在控制过程中由系统的状态改变会改变系统的马尔科夫参数，但在状态变化不大的情况下，由当前状态线性化得到的马尔科夫参数仍然可以很好地满足系统控制要求，这也验证了由局部线性化设计得到的RCAC算法参数可以适用于NASA-GTM这种复杂的非线性系统中.

图2给出了两个变化的动力学参数，其中由于系统状态(主要是攻角)的改变，CL0与CD0会同时发生变化.图3为系统输出，可以看出在500 s以后，系统仍然可以很好的保持当前的状态.图4给出了部分系统的状态与控制量，RCAC控制器通过引擎输出增长来补偿阻力的增加，然后通过增加攻角来提高升力系数进而保持飞机高度与速度.图2中可以看出由于CL0的增加，CL基本保持了原来的值.由于仿真时控制器增益的初始值全部设为零，所以会产生仿真初始阶段的震荡.图2～图4中开始一段的震荡是控制器在开始自适应调节控制增益时的系统状态过渡过程.图5给出了RCAC控制器增益的变化，可以看出500 s到1 000 s期间，控制器增益由于CL0与CD0而自适应的改变来保持系统输出的稳定.

图2 气动力学参数

图3 GTM模型状态输出

图4 相关的系统状态与系统输入

图5 控制器增益

3 控制舵面卡死情况下的自适应控制

本节主要进行飞机副翼舵面卡死情况下的自适应控制研究.目标的系统输出包括飞机的3个平稳飞行状态量［17］，分别是空速VT、航迹角γ与转弯速度在t=200 s时，飞机副翼舵面逐渐偏转到-2°然后卡死.RCAC控制器参数配置为:

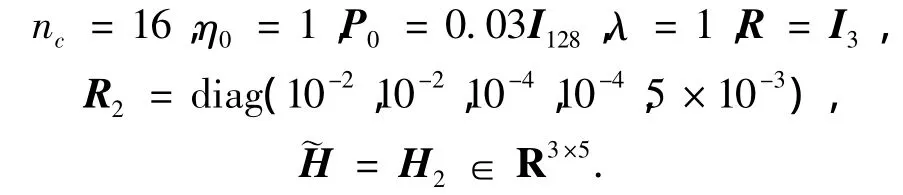
图6为系统平稳状态量输出.可以看出在t=200 s时由于横滚舵面卡死，系统输出状态产生了一些小的波动，但是很快就重新稳定.在t=300 s时，开始给定平稳飞行状态控制指令，使飞机在平稳状态之间过渡，由此可见，在横滚舵面卡死的情况下，飞机依然可以很好的跟踪控制指令.图 7 为飞机的控制量输入，包括δe、δa、δr、δLT与δRT，其中δa由于故障卡死在-2°，无法跟踪给定控制量，但是通过其他4个控制量的调节，使飞机系统故障得到了很好的补偿.在系统仿真的最初阶段，由于控制器增益的初始值为零，在自适应的调节控制器增益过程中，系统的各个变量会产生短暂的震荡.图8给出了RCAC控制器增益的变化，可以看出控制器增益由于横滚舵面的卡死而自适应的改变来保证控制指令的跟踪.

图6 GTM模型状态输出

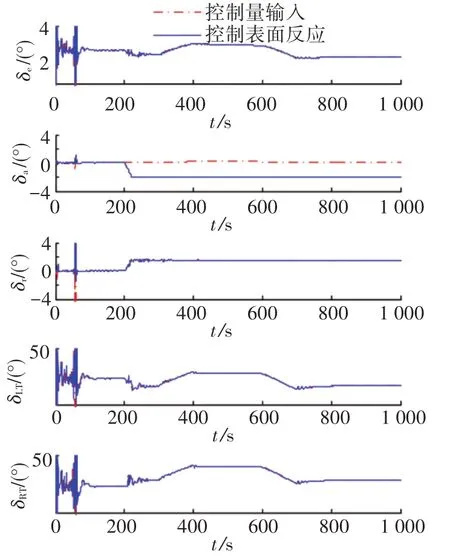
图7 GTM模型控制量输入

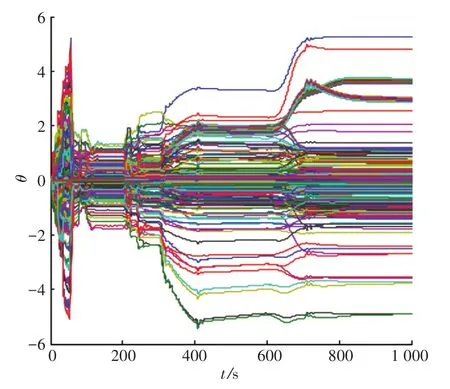
图8 控制器增益

4 结语

基于NASA-GTM通用飞机模型，在未知故障情况下应用回顾成本自适应控制方法(RCAC)对其进行飞行稳定控制.通过近似模拟机体结冰情况下部分飞行动力学参数变化来测试RCAC控制器在此情况下的控制效果.仿真结果表明RCAC能够很好的自适应调节控制器增益来补偿未知的动力学参数改变.当阻力系数增加80%同时升力系数减小了25%的情况下，RCAC控制器通过提高引擎输出和增大飞机攻角来保持飞行高度与速度;当飞机副翼舵面卡死在一定角度时，RCAC可以通过调节其他4个控制量以保证飞机的平稳飞行状态，同时也可以很好跟踪控制指令.

［1］BLANKE M.Diagnosis and fault-tolerant control［M］.Berlin:Springer，2003.

［2］DASGUPTA D，KRISHNA KUMAR K，WONG D，et al.Negative selection algorithm for aircraftfault detection［C］//In Artificial Immune Systems:Proceedings of ICARIS 2004.Berlin:Springer，2004:1-13.

［3］BRAGG M B，HUTCHISON T，OLTMAN R，et al.Effect of ice accretion on aircraft flight dynamics［R］.Reston VA:AIAA，2000.

［4］于庆芳.Y12─Ⅱ型飞机结冰对其飞行特性影响的试飞研究［J］.飞行力学，1995(2):63-70.

［5］李林，王立新，彭小东.结冰对民机飞行性能的影响研究［J］.飞行力学，2004，22(3):12-16.

［6］张爱华，胡庆雷，霍星.过驱动航天器自适应姿态补偿控制及控制分配［J］.哈尔滨工业大学学报，2014，46(1):18-22.

［7］RYSDYK R T，CALISE A J.Fault tolerant flight control via adaptive neural network augmentation［C］//AIAA Guidance，Navigation， and Control Conference and Exhibit.Reston VA:AIAA，1998:1722-1728.

［8］ KANESHIGE J，BULL J，TOTAH J.Generic neural flightcontroland autopilot system ［C］//AIAA Guidance，Navigation，and Control Conference.Reston VA:AIAA，2000:AIAA 2000-4281.

［9］NGUYEN N，KRISHNAKUMAR K，KANESHIGE J，et al.Flight dynamics and hybrid adaptive control of damaged aircraft［J］.Journal of Guidance，Control，and Dynamics，2008，31(3):751-759.

［10］PAGE A B，MELONEY E D，MONACO J F.Flight testing of a retrofit reconfigurable control law architecture using an F/A - 18C ［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston VA:AIAA，2006:AIAA 2006-6052.

［11］HOAGG J B，BERNSTEIN D S.Retrospective cost model reference adaptive control for nonminimum-phase systems ［J］. Journal of Guidance， Control， and Dynamics，2012，35(6):1767-1786.

［12］SANTILLO M A，BERNSTEIN D S.Adaptive control based on retrospective cost optimization［J］.Journal of Guidance，Control，and Dynamics，2010，33(2):289-304.

［13］D'AMATO A M，SUMER D，MITCHELL K，et al.Adaptive output feedback control of the NASA GTM model with unknown nonminimum-phase zeros［C］//AIAA Guidance，Navigation，and Control Conference.Reston VA:AIAA，2011:AIAA 2011-6204.

［14］SOBOLIC F M，BERNSTEIN D S.Aerodynamic-free adaptive control of the NASA generic transport model［C］//AIAA Guidance， Navigation， and Control Conference and Exhibit.Reston VA:AIAA，2013:AIAA 2013-4999.

［15］YU M J，RAHMAN Y，ATKINS E M，et al.Minimal modeling adaptive controlofthe NASA Generic Transport Model with unknown control-surface faults［C］//AIAA Guidance， Navigation， and Control Conference and Exhibit.Reston VA:AIAA，2013:AIAA 2013-4693.

［16］ZHONG J，RAHMAN Y，YAN J，et al.Retrospective cost model refinement for on-line estimation of constant and time-varying flight parameters ［C］//AIAA Guidance， Navigation， and Control Conference and Exhibit.Reston VA:AIAA，2013:AIAA 2013-5193.

［17］YI G，ATKINS E M.Trim state discovery for an adaptive flight planner［C］//Proceedings of the 48th AIAA Aerospace Science Meeting.Reston VA:AIAA，2010:AIAA 2010-416.