树的3-彩虹控制数的上界

梁冰冰，皮晓明，刘焕平

（哈尔滨师范大学数学系，黑龙江 哈尔滨 150025）

树的3-彩虹控制数的上界

梁冰冰，皮晓明，刘焕平

（哈尔滨师范大学数学系，黑龙江 哈尔滨 150025）

对树的3-彩虹控制数进行研究，首先用构造法找到直径较小的树的3-彩虹控制数的上界.再通过分类讨论思想和数学归纳法得到一般的阶n大于等于5的树的3-彩虹控制数的上界.

树；控制数；彩虹控制数

DO I：10.3969/j.issn.1008-5513.2015.02.012

1 引言

1962年，文献［1］首先给出了控制数的数学定义.同时，随着科学技术的进步和实际问题的发展，国内外许多学者开始研究各种类型的控制函数.2005年，文献［2］提出了彩虹控制数的概念.在以后的几年里，一些数学家陆续给出了有关彩虹控制数的相关结论.文献［3］证明了对于任意的正整数k，图的k-彩虹控制数是一个NP完全问题.这说明对于图的k-彩虹控制数的研究是非常困难的.文献［4］给出路和圈的2-彩虹控制数以及Petersen图的2-彩虹控制数的上界.在这基础上，文献［5］给出树的2-彩虹控制数的关于顶点个数的上界和关于最大顶点度的下界，还给出了一般连通图的2-彩虹控制数的关于直径的上界和下界.2014年，文献［6］得到了路、圈、Petersen图的3-彩虹控制数以及一般连通图的3-彩虹控制数的上界.特别地，得到

引理1.1［6］若 n≥5，则

2 预备知识

本文中的图G都是连通的无向简单图.V（G）表示图G的顶点集，E（G）表示图G的边集.设S⊆V（G）,称

给定一个图G和正整数k，图G的k-彩虹控制函数f是指满足下列条件的映射f：V（G）→2｛1，2，··，k｝，使得若顶点v满足f（v）=∅，则

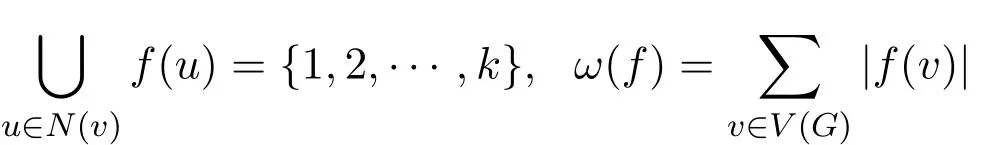
是k-彩虹控制函数f的权.图G的k-彩虹控制数γrk（G）=m in｛ω（f）|f是G的k-彩虹控制函数｝.G的具有权γrk（G）的k-彩虹控制函数称为最小k-彩虹控制函数.与一个一度点相邻的点称为支撑点，与一度点相关联的边称为悬挂边.边的n度细分是从图G中删去一条边uv，并用一条与G中点内部不交的长为n+1的路连接u，v.边的树枝化是把G的一条边一度细分后变成uwv，在w处附着一条悬挂边.边的星化是把G的一条边一度细分后变成uwv，在w处附着至少两条悬挂边，w称为星化点.

图1 A，B，C三种子图

树枝型图是把星图的至少一条边星化，树枝化或一度细分得到的非路的图；星图的中心称为树枝型图的中心，度大于等于4的非中心的支撑点称为树枝型图的次中心.伸长型图是在树枝型图或星图的中心u处至少附着图b、图c两种子图之一的非路的图；树枝型图或星图的中心称为伸长型图的中心，树枝型图的次中心称为伸长型图的次中心.手指型图G是在星图K1，m的一些边上最多2度细分后得到的图G′上，添加顶点集V′和边集E′使每一顶点v∈V′恰与V（G′）−V（K1，m）的一个顶点相邻，在此基础上，再在K1，m的中心u处附着至少一个图1中A型子图得到的非路的图；星图的中心u称为手指型图的中心.

3 主要结果及证明

对星图显然有下面结论成立：

定理3.1 若G是阶n≥4的星图，则γr3（G）=3.

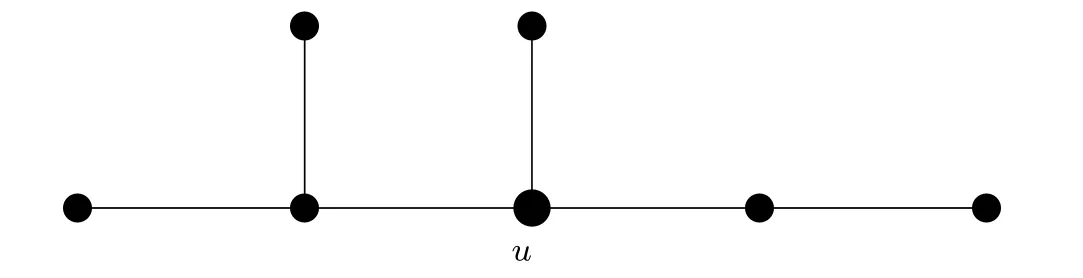
图2 a=0，b=c=d=1

证明 设 G是在星图 K1，m中分别星化，树枝化和一度细分 a,b,c条边后得到的图，令d=m−a−b−c，u是G的中心，则n≥4a+3b+2c+d+1且a+b+c≥1.令X=｛x∈V（G）|x是G的次中心｝，接下来分以下情形讨论.

情形1 d≥3或d=2且b+c≥1.令

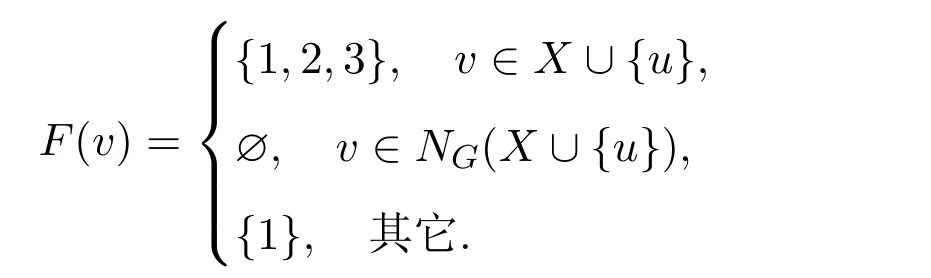
则 F是G的一个3-彩虹控制函数，且ω（F）=3a+2b+c+3，于是

情形2 d=2且b+c=0或d≤1,a=c=1,b=0.令

则F是G的一个3-彩虹控制函数，且ω（F）=3a+2c+d，于是

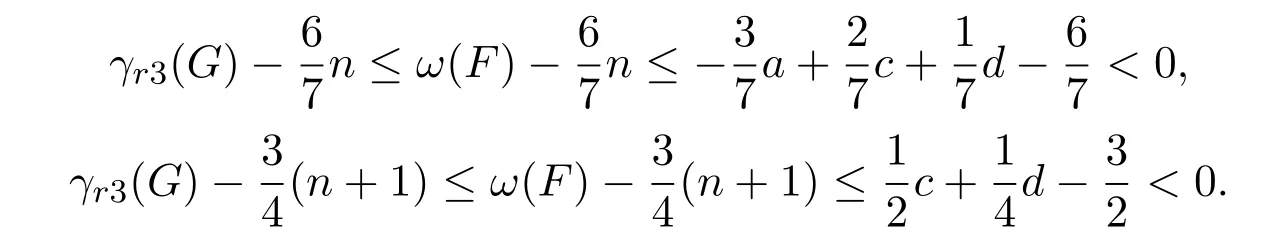
则F是G的一个3-彩虹控制函数，且ω（F）=3a+2b+c+d+2，于是

若两个不等式等号同时成立，则γr3（G）=ω（F）,n=4a+3b+2c+d+1且

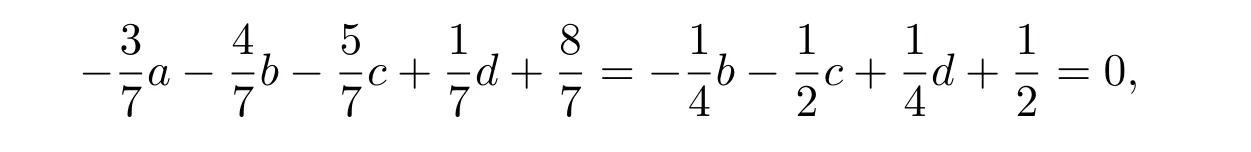
综上所述，当且仅当G是图2所示的图时，上述两个不等式的等号同时成立.

情形4 d≤1,c=0.令

对于任意的v∈N，令

其中p1（v）,p2（v）是v的两个一度邻点.对于其他的点v∈V（G）−N1，令

则F是G的一个3-彩虹控制函数，且ω（F）=3a+2b+d+1，于是

图3 a=c=e=0，b=d=f=1

证明 设G′是在星图K1，m中分别星化，树枝化和一度细分a,c,e条边得到的树枝型图，则G是通过在G′的中心或星图的中心u处分别附着b个B型子图和d个C型子图得到的伸长型图.令f=m−a−c−e，则n≥4（a+b）+3（c+d）+2e+f+1且b+d≥1.接下来分以下情形讨论.令X=｛x∈V（G）|x是G的次中心｝.

情形1 f≥2.令

则F是G的一个3-彩虹控制函数，且ω（F）=3（a+b）+2（c+d）+e+3，于是

情形2 f≤1,d+e≥1.令

则F是G的一个3-彩虹控制函数，且ω（F）=3（a+b）+2（c+d）+e+f+2，于是

若两个不等式等号同时成立，则

综上所述，当且仅当G是图3所示的图时，两个不等式的等号同时成立.

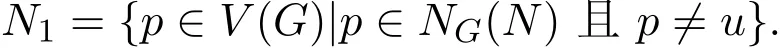
对于任意v∈N，令F（p1（v））=｛2｝,F（p2（v））=｛3｝，其中p1（v）,p2（v）是v的两个非中心的邻点.对于其他的点v∈V（G）−N1，令

则F是G的一个3-彩虹控制函数，且ω（F）=3（a+b）+2c+f+1，于是

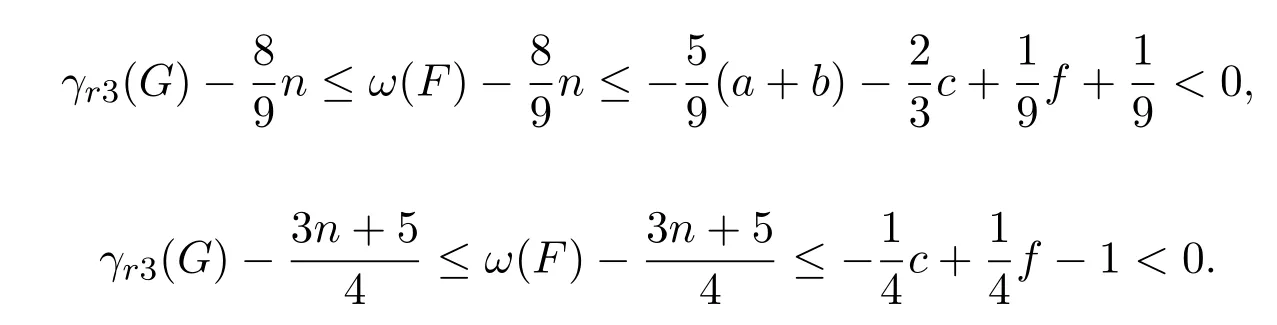
证明 对于手指型图G，删除G的中心u后得到一些子图，把这些子图中的阶大于等于5的树枝型图和阶大于等于4的星图的并记为G1，则由引理3.1和定理3.1知

于是 G2=G−G1只包含图 4中的6种子图，记 G2包含以下6种子图的个数依次为a,b,c,d,e,f，

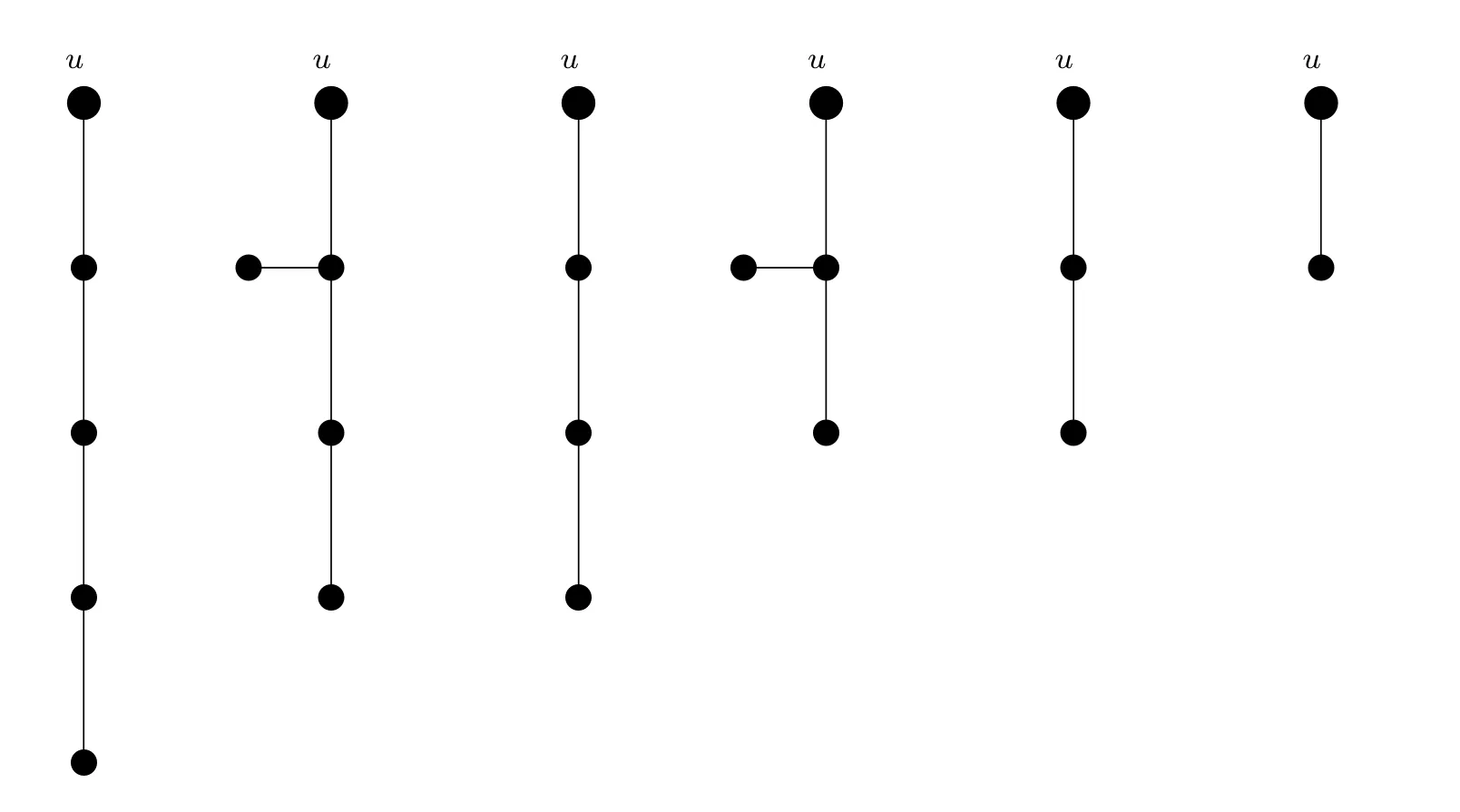
图4 G2的几种子图

则|V（G2）|=n2=4（a+b）+3（c+d）+2e+f+1且a≥1.接下来分以下情形讨论.

情形1 f≥2.令

则F2是G2的一个3-彩虹控制函数，且ω（F2）=3（a+b）+2（c+d）+e+3，于是

情形2 f≤1,e+c≥1.令

则F2是G2的一个3-彩虹控制函数，且ω（F2）=3（a+b）+2（c+d）+e+f+2,于是

若不等式等号成立，则

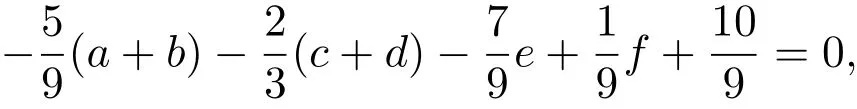
且结合情形2的条件及a≥1得，只能是a=c=f=1,b=d=e=0（如图5）.反过来，设G2是图4所示的图，则G2中除中心u外所有点的度均小于等于2.假设G2的3-彩虹控制数不超过7且是G2的最小3-彩虹控制函数，则必有而其余点在下的值都是一元集，其中v是G2中一个不同于u的顶点，这是不可能的.所以G2的3-彩虹控制数大于等于8.从而设G是n（≥5）阶的3-彩虹控制数为的手指型图，则由引理3.2及上述证明知，G=G2或G是通过在图3和图5的中心之间连边得到的图，但后者显然不是手指型图，所以G=G2.于是当且仅当G是图5所示的图时，不等式的等号成立.

图5 a=c=f=1，b=d=e=0

对于任意v∈N，令F（p1（v））=｛2｝,F（p2（v））=｛3｝，其中p1（v）,p2（v）是v的两个非中心的邻点.对于其他的点v∈V（G2）−N1，令

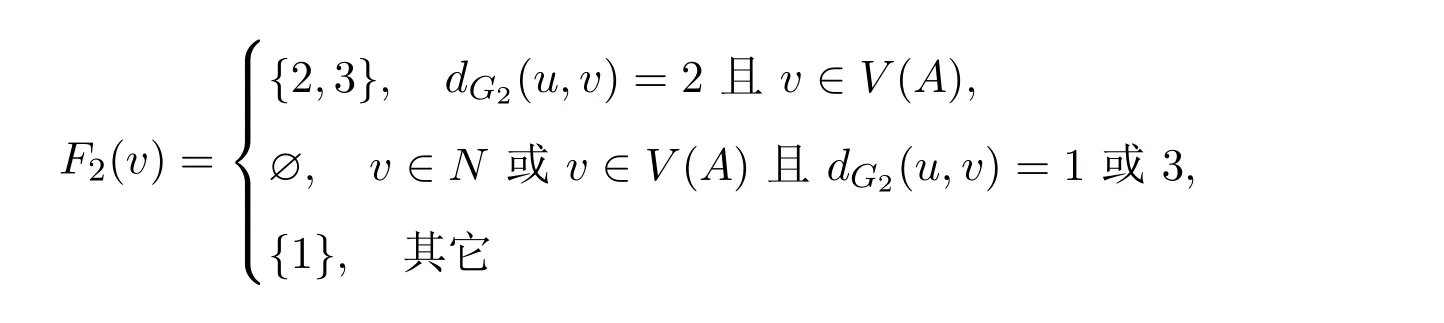
其中A是手指型图G的中心u处附着的图1中的A型子图，则F2是G2的一个3-彩虹控制函数，且ω（F2）=3（a+b）+2d+f+1，于是

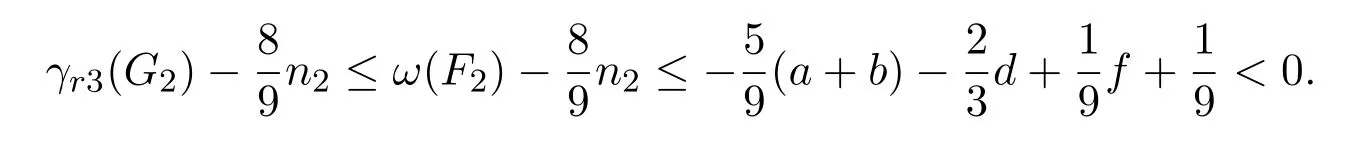
设F1是G1的最小3-彩虹控制函数，定义

则F是G的一个3-彩虹控制函数，且

证明 用归纳法进行证明，先考虑一些直径较小的树.

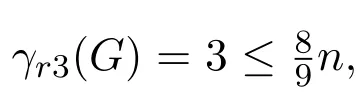
情形2 3≤diam（T）≤4.则T是一个n≥5的路或树枝型图，由引理1.1及推论3.1知，结论成立.

情形 3.1 n1≤4,n2≤4.显然T1或T2中每个顶点的度均不大于3，且T中至少有一个点h的度等于3，令F（h）=｛1,2,3｝,

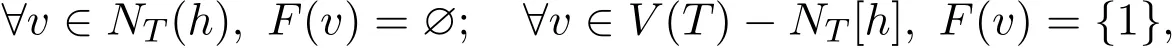
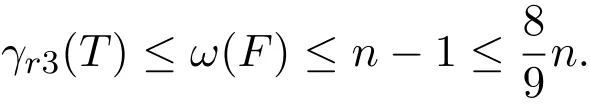
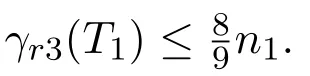
当T2不是一个n2=4的星图时，T是一个以u1为中心的伸长型图，由推论1知，结论成立.

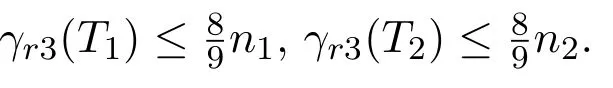
结论成立.

情形 4 6≤diam（T）≤8.选取T的最长路P，使与P的端点相邻的支撑点v的度最大，令v,u,t,x分别是P上依次相邻的顶点，分以下情形讨论.

情形4.2 dT（v）=3且dT（u）＞2.设T−ut的两个连通分支为树T1,T2，令含v的分支为T1，显然T1的阶至少为5，通过与情形4.1类似的讨论得结论成立.

情形 4.3 dT（v）=2.当dT（u）＞3时，通过与情形4.2类似的讨论知结论成立.下设dT（u）≤3.

情形 4.3.1 dT（u）=3.若u不是支撑点，通过与情形4.2类似的讨论知结论成立.设u是支撑点，且T−tx的两个分支是阶分别为n1和n2的树T1和T2，令含t的分支为T1，显然n1≥5.当n2≥5时，由归纳假设，易证结论成立.设n2≤4，则diam（T）≤7.

情形4.3.1.1 dT（t）=2.当diam（T）=6时，若T中除u外的所有顶点的度都小于3，则n=8，令F（u）=｛1,2,3｝,对任意的v∈NT（u）,F（v）=∅，对任意的

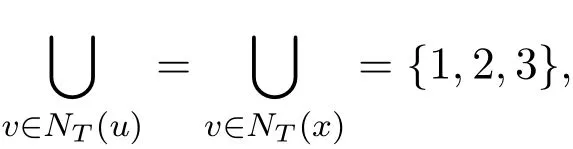
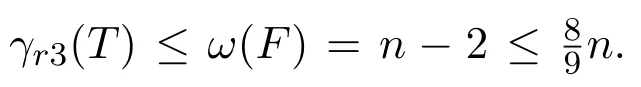
情形4.3.1.2 dT（t）＞2.当diam（T）=6时，由前面的讨论和v的选取及x与u的对称性知，只需讨论dT（x）=2或dT（x）=3且x是支撑点的情形.无论是前者还是后者，T都是一个以t为中心的伸长型图.当diam（T）=7时，T是一个以t为中心的手指型图，由推论3.1知，结论成立.

情形4.3.2 dT（u）=2.由v的选取及前面的讨论知，P上与P的另一端点相邻的点和与之距离为2的点的度均为2，于是只需讨论P上与P的另一端点距离为3和4的点的度的情形.

情形 4.3.2.1 dT（t）＞2.T−tx把T分为阶分别是n1和n2的树T1和T2.令含t的树为T1，则n1≥5.当n2≥5时，由归纳假设易证结论成立；否则diam（T）≤7，此时，T是一个以t为中心的伸长型图或手指型图，由推论3.1知，结论成立.

情形 4.3.2.2 dT（t）=2.当diam（T）=6或7时，T为n=7或8的路，由引理1.1知，结论成立.当diam（T）=8时，若dT（x）=2，T是n=9的路，由引理1.1知，结论成立.若dT（x）≥2，T是一个手指型图，由推论3.1知，结论成立.

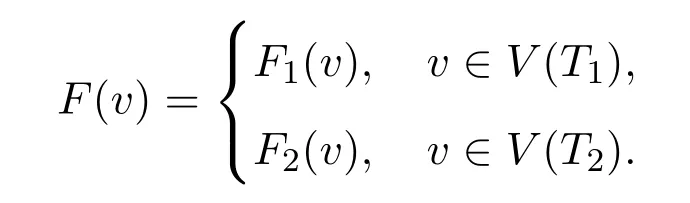
则F是T的一个3-彩虹控制函数，于是

［1］Ore O.Theory of Graphs［M］.USA：Amer.Math.Soc.Colloq.Publ.，1962.

［2］Bre˘sar B，Henning M A，Rall D F.Paired-dom ination of Cartesian products of graphs and rainbow dom ination［J］.Electron.Notes Discrete Math.，2005，22：233-237.

［3］Chang C J，W u J J，Zhu X D.Rainbow dom ination on trees［J］.Discrete App l.M ath.，2010，158：8-12.

［4］Bre˘sar B，Sumenjak T K.On the 2-rainbow dom ination in graphs［J］.Discrete App l.M ath.，2007，155：2394-2400.

［5］Wu Y J，Rad N J.Bounds on the 2-rainbow dom ination number of graphs［J］.G raphs Combin.，2013，29：1125-1133.

［6］Shao ZH，Liang M L，Yin C，et al.On rainbow dom ination numbers ofgraphs［J］.Inf.Sci.，2014，254：225-234.

2010 M SC：05C69

U pper bounds on the 3-rainbow dom ination num ber o f trees

Liang Bingbing，Pi Xiaom ing，Liu Huanping
（School of M athem atical Sciences，Harbin Norm al University，Harbin 150025，China）

This paper studies 3-rainbow dom ination number of trees.First we give an upper bound for the 3-rainbow dom ination number of treesw ith small Geter by the construction method.Second，we give an upper bound on the 3-rainbow dom ination number of trees w ith order n equaling or greater than 5 by induction and the idea of classif cation discussion.

tree，dom ination number，rainbow dom ination number

O157.5

A

1008-5513（2015）02-0210-11

2017-04-02.

黑龙江省教育厅科学技术研究项目（12531203；12521148）；哈尔滨师范大学青年学术骨干项目基金（10XBKQ 08）.

梁冰冰（1989-），硕士生，研究方向：组合数学与图论.

皮晓明（1977-），副教授，硕士生导师，研究方向：图论与组合最优化.