一类具有保护区域的Leslie-Gow er捕食-食饵模型的分歧分析

姜启芳，崔仁浩，刘萍

（哈尔滨师范大学数学科学学院，黑龙江 哈尔滨 150025）

一类具有保护区域的Leslie-Gow er捕食-食饵模型的分歧分析

姜启芳，崔仁浩，刘萍

（哈尔滨师范大学数学科学学院，黑龙江 哈尔滨 150025）

研究了一类Neumann边界条件下带有保护区域的Leslie-Gower捕食-食饵模型，分析稳态系统从半平凡解处发生分歧的条件，得到了分歧方向及分歧值的唯一性，得到了在确定参数范围内，从半平凡解出发的分支解曲线的稳定性.

保护区域；捕食-食饵模型；分歧；唯一性；稳定性

DO I：10.3969/j.issn.1008-5513.2015.02.004

1 引言

捕食-食饵模型是用来描述两物种之间相互作用关系的微分方程模型.最早由美国的化学生物学家Lotka［1］和意大利的数学家Volterra［2］提出.其形式为：

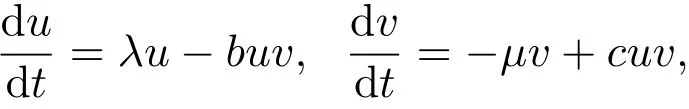
其中λ,µ,b,c＞0.考虑到捕食者捕食食饵的能力是有限的，Solomon［3］和Holling［4］引进了捕食者的响应函数，其中带有Holling II型响应函数的捕食-食饵模型具有如下形式：

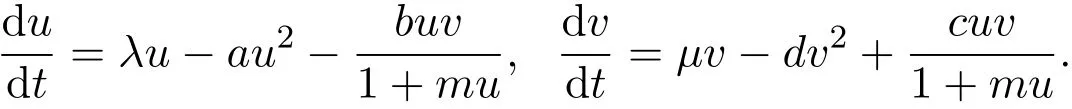
反应扩散系统也被称为扩散种群系统，其形式为：

在捕食-食饵型的反应扩散系统中，为食饵建立一个保护区域是指食饵可以自由进出保护区域，而捕食者只能生活在保护区域以外.文献［5］考虑了保护区域对带有强A llee效应的捕食-食饵型反应扩散系统的影响.文献［6］应用稳态分歧和Hope分歧理论研究了带有Holling II型响应函数的捕食-食饵模型的非常数稳态解和周期解的存在性和稳定性.文献［7］研究了带有Holling II型响应函数的扩散Leslie-Gower捕食-食饵模型的正稳态解的存在性、多解性、唯一性及分歧结构.

继续文献［7］的研究工作，本文研究Neumann边界条件下带有保护区域的Leslie-Gower捕食-食饵模型：

2 预备知识

首先介绍本文的主要工具-著名的Crandall-Rabinow itz单参数分歧定理.

引理 2.1［8］若U是（λ0,u0）∈R×X的一个邻域，F：U→Y是一个二次连续可微映射，对于任何（λ,u0）∈U，F（λ,u0）=0，在（λ0,u0）处F满足

和

其中N（Fu（λ0,u0））=span｛ω0｝.设Z是span｛ω0｝在X中的一个补空间，则F（λ,u）=0的解集在（λ0,u0）附近为一条连续可微的曲线

其中λ（0）=λ0,z（0）=z′（0）=0.进一步地可知，

如果λ′（0）=0,且F在（λ0,u0）附近是三次连续可微的，则

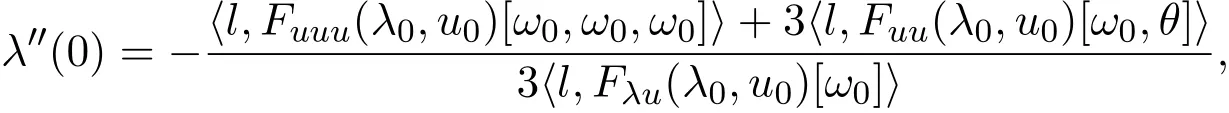
其中θ满足

引理 2.2［9］令F,Z,λ0,ω0如引理2.1定义，且（λ（s）,u（s））是引理2.1定义的解曲线.假设对任意K∈B（X,Y）,µ=0是 Fu（λ0,u0）的K-单特征值.那么存在ε＞0,γ∈C1, γ：（λ0−ε,λ0+ε）→R,µ：（−ε,ε）→R,v：（λ0−ε,λ0+ε）→X,ω：（−ε,ε）→X使得

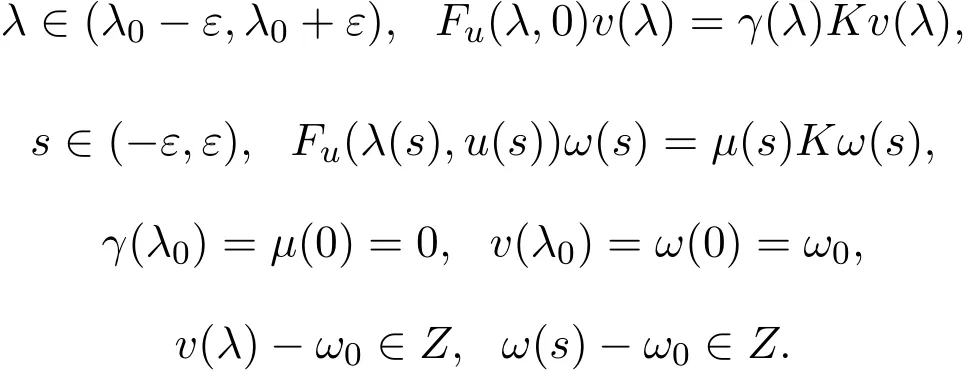
3 从半平凡解出发的分歧

考虑模型（1）的稳态系统：

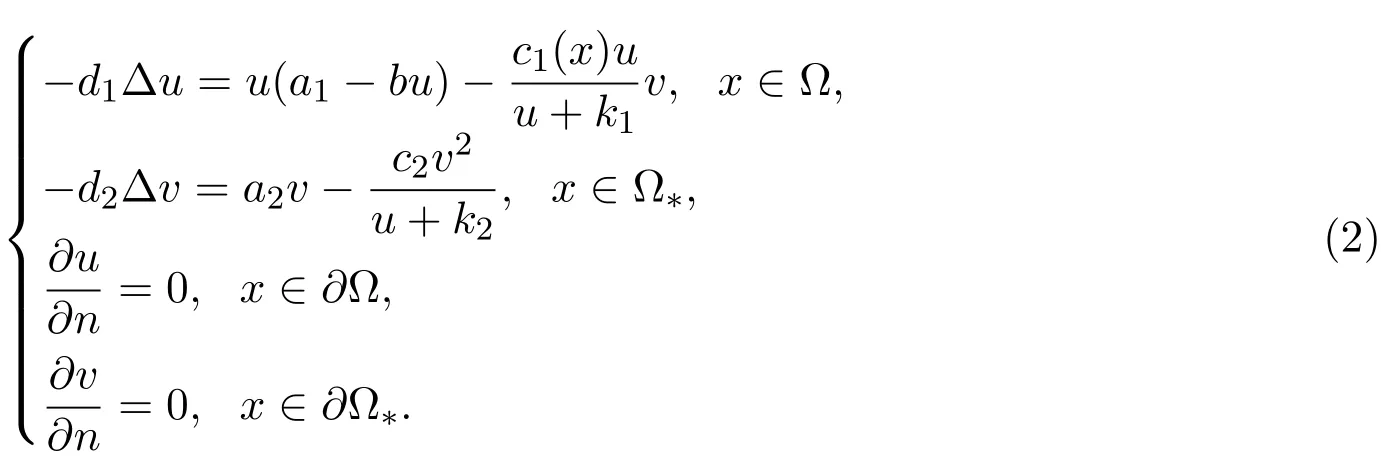
应用引理2.1，以a1为分歧参数，考虑稳态方程组（2）从半平凡解Γ处分支出来正解的解曲线，其中

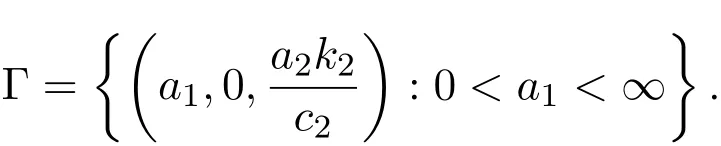
对任意p＞N，定义

以及

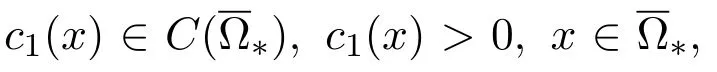
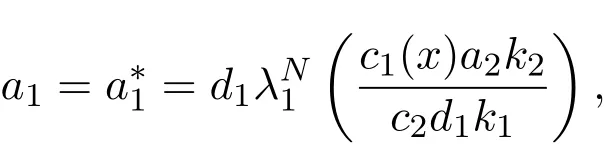
（a1（s）,u（s）,v（s））是关于s的光滑函数，并且满足

其中ϕ＞0是

证明 定义映射F：R×X1×X2→Y1×Y2,

首先给出F在（a1,u,v）处的Frchet导数

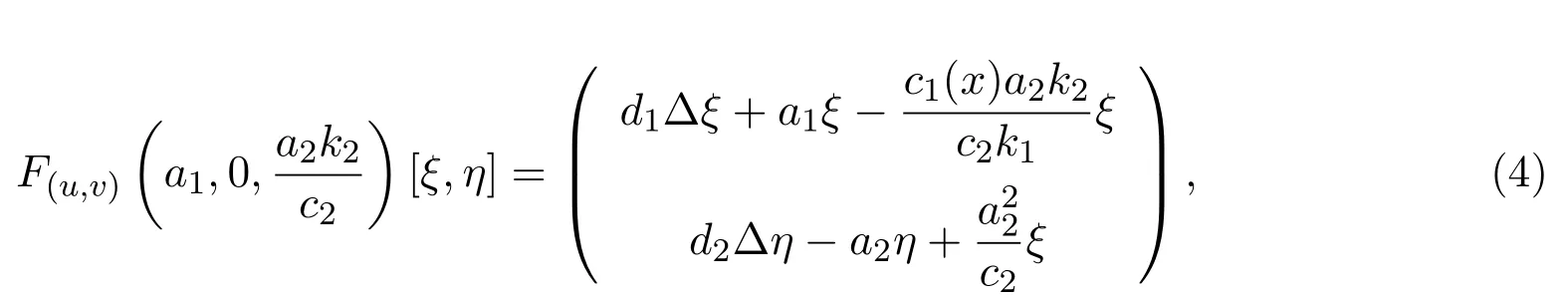
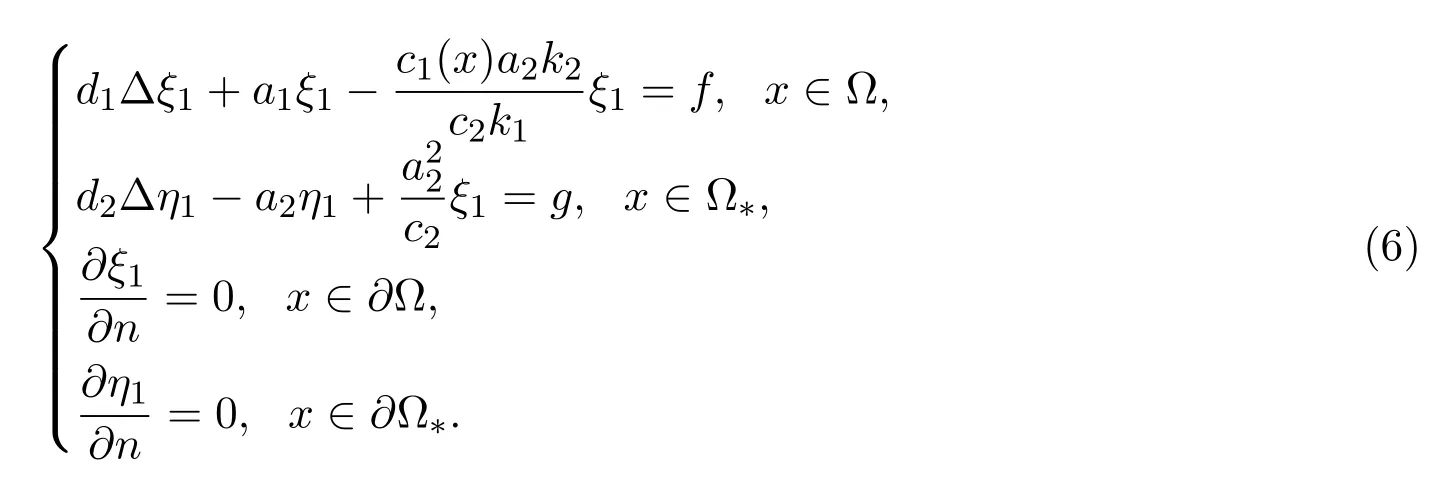
将（5）式的第一个式子乘以ξ1，（6）式的第一个式子乘以ϕ，两式积分相减得到

这样

即

又因为

所以

进一步，有

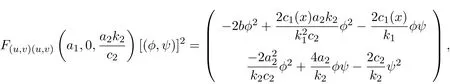
故

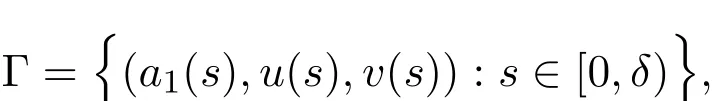
且满足

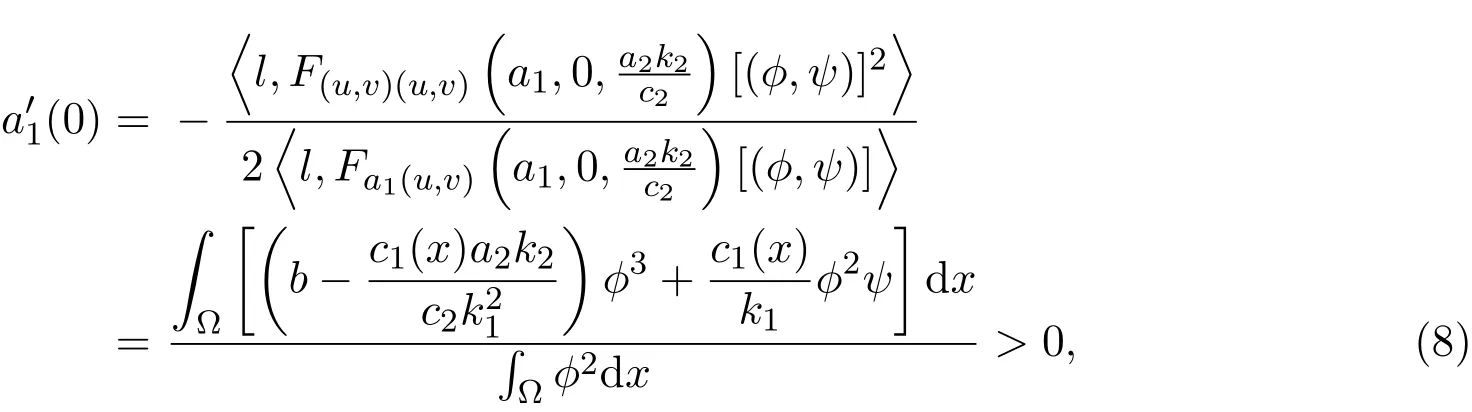
其中l定义为：

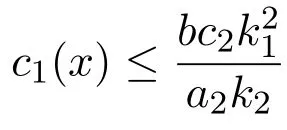
将（a1n,un,vn）代入系统（2）的第一个式子并在等式两端同时除以∥un∥Lp（Ω）.对任意n≥1,有

等价于

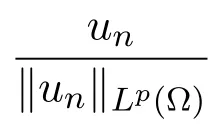
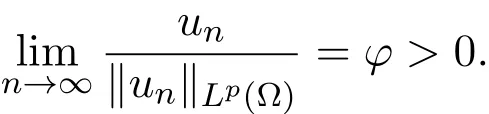
这样，当n→∞时，

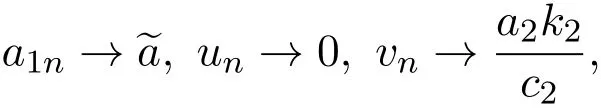
对（10）式两端取极限，则有

等价于

将（5）式的第一个式子乘以φ,（11）式的第一个式子乘以ϕ,两式在Ω上积分相减得

4 分歧解支的稳定性

最后讨论从半平凡解发生分歧解支的稳定性.

证明 令（a1,u,v）=（a1（s）,u（s）,v（s））.那么系统（2）在（u,v）处的线性化可表示为：

其中

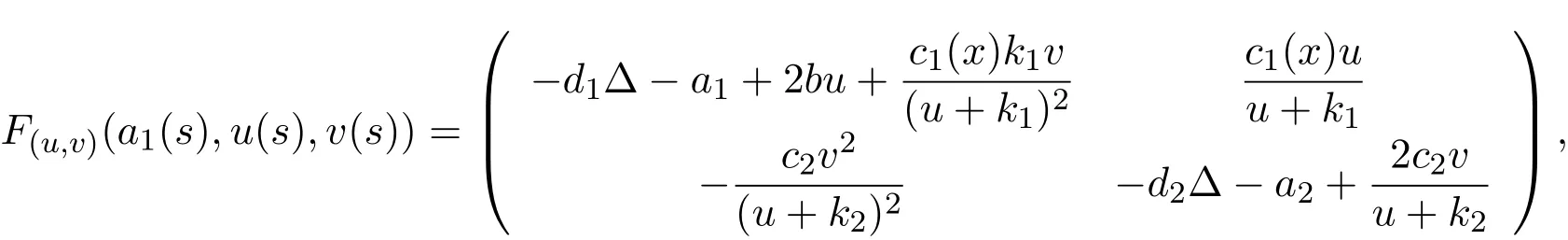
令s→0+,有

由线性算子的小扰动理论［10］，对充分小的s＞0,F（u，v）（a1（s）,u（s）,v（s））有唯一特征值µ（s）,满足当s→0+时，µ（s）→0,F（u，v）（a1（s）,u（s）,v（s））的所有其他特征值的实部是正的.记

对任意s＞0,确定Re（µ）的符号.令（ξ,η）为特征值µ所对应的特征函数，使得当s→0+时，（ξ,η）→（ϕ,ψ）,那么（ξ,η）满足：

将（12）式的第一个式子两端同时乘以u,然后在Ω上积分，得到

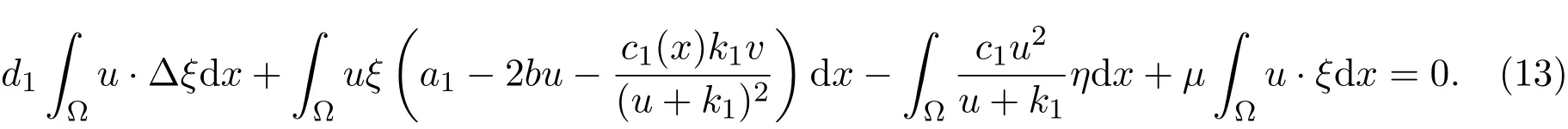
在系统（2）的第一个式子两端乘以ξ,然后在Ω上积分且由（u,v）=（u（s）,v（s）），得到

两式相减得

即

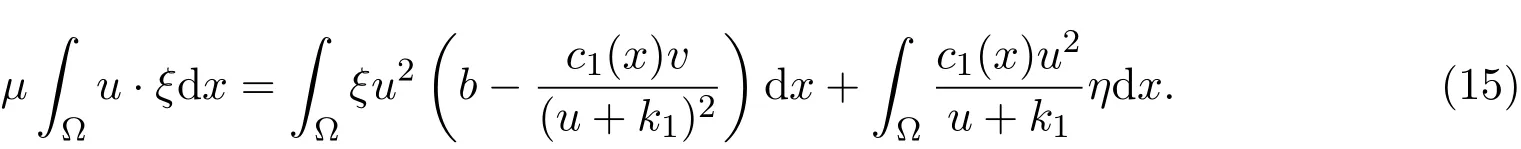
因为当s→0+时，（ξ,η）→（ϕ,ψ）,由（7）式

可得

在（15）式中取实部，同时除以s2,令s→0+,由（8）式，有

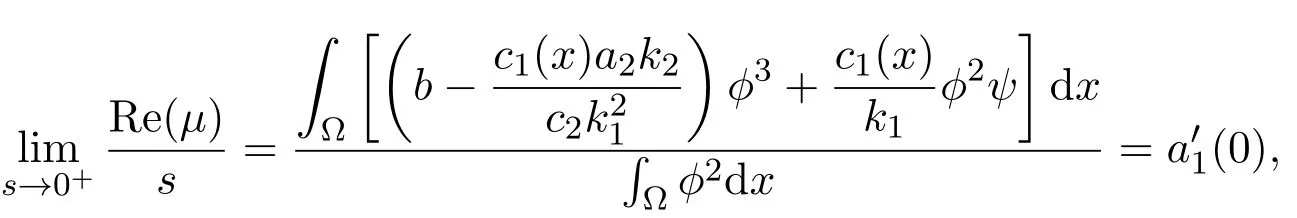
且（u（s）,v（s））是稳定的.

［1］Lotka A J.Analytical note on certain rhythm ic relations in organic system s［J］.Proc.Natl.Acad.Sci.，1920，6：410-415.

［2］Volterra V.Fluctuations in the abundance of species，considered m athem atically［J］.Nature，1926，118：558 -560.

［3］Solom on M E.The natural control of anim al popu lations［J］.J.Anim.Ecol.，1949，18：1-35.

［4］Holling C S.Some characteristics of sim p le types of predation and parasitism［J］.Canadian Entomologist，1959，91：385-398.

［5］CuiR H，Shi JP，Wu B Y.Strong A llee ef ect in a dif usive predator-prey system w ith a protection zone［J］. J.D if erential Equations，2014，256：108-129.

［6］Yi F Q，Wei J J，Shi J P.Bifurcation analysis of a dif usive predator-prey system w ith Holling type-II funcation response［J］.J.Dif erential Equations，2009，246：1944-1977.

［7］Zhou J，Shi JP.The existence，bifurcation and stability of positive stationary solutions of a dif usive Leslie-Gower predator-prey m odelw ith Holling-type II function responses［J］.J.M ath.Anal.App l.，2013，405：618-630.

［8］Crandall M G，Rabinow itz P H.Bifurcation from sim p le eigenvalues［J］.J.Funct.Anal.，1971，8：321-340.

［9］Crandall M G，Rabinow itz P H.Bifurcation，perturbation of sim p le eigenvalues and linearized stability［J］. Aech.Rational M ech.Anal.，1973，52：161-180.

［10］Kato T.Perturbation Theory for Linear Operators［M］.New York：Springer，1996.

2010 M SC：35B32

B ifu rcation analysis in a class of Leslie-Gow er p redator-p rey m odel w ith a p rotection zone

Jiang Qifang，Cui Renhao，Liu Ping
（School of Mathematical Science，Harbin Normal University，Harbin 150025，China）

In this paper，we consider a class of Leslie-Gower predator-prey system w ith p rotection zone for the prey under Neum ann boundary condition.The bifurcation condition and direction from the sem i-trivial solution are analyzed and the uniqueness of the bifurcation value is obtained.Moreover，we show the stability of the positive solutions bifurcating from the sem i-trivial solution under certain conditions.

protection zone，predator-prey m odel，bifurcation，uniqueness，stability

O175.23

A

1008-5513（2015）02-0136-10

2014-11-04.

国家自然科学基金（11401144）；黑龙江省留学归国人员科学基金（LC2013C01）.

姜启芳（1989-），硕士生，研究方向：偏微分方程.

刘萍（1977-），博士，教授，研究方向：偏微分方程.