Filiform李代数Q n的H om-结构

于欢欢，刘文德

（哈尔滨师范大学数学科学学院，黑龙江 哈尔滨 150025）

Filiform李代数Qn的H om-结构

于欢欢，刘文德

（哈尔滨师范大学数学科学学院，黑龙江 哈尔滨 150025）

首先证明了有限维Z-阶化李代数上的一个线性算子是Hom-结构的充分必要条件，即它的每个齐次分支也是Hom-结构.然后计算了特征零代数闭域上一类有限维Z-阶化Filiform李代数Qn的齐次Hom-结构，从而决定了Qn的所有Hom-结构.

Filiform李代数；阶化结构；Hom-结构

DO I：10.3969/j.issn.1008-5513.2015.02.006

1 引言

2006年，文献［1］在研究W itt代数和Virasoro代数的量子形变时，引进了Hom-李代数的概念.粗略地说，Hom-李代数是带有一个斜对称双线性乘法和一个线性算子的代数，并且满足Hom-Jacobi恒等式.Hom-李代数是李理论的一个重要方向，与李代数等重要代数结构有着密切关系.近几年关于Hom-李代数的研究非常活跃.例如：2011年，文献［2］刻画了Hom-代数的同调和形变.2012年，文献［3］给出了Hom-李代数的伴随表示、平凡表示以及它的导子、形变、中心扩张等.

近年来对一类代数Hom-结构的研究也比较活跃.例如：2008年，文献［4］计算了特征零代数闭域上的半单李代数的所有保积Hom-结构.2013年，文献［5］证明了复数域上有限维单李超代数的保积Hom-结构一定是0或者是恒等自同构.2014年，文献［6］刻画了特征零上的8类无限维单的向量场李超代数的Hom-结构，证明了这些单的向量场李超代数的不保积Hom-结构都是纯量，并进一步证明了这些单的向量场李超代数的保积Hom-结构一定是0或者是恒等自同构.同年，文献［7］计算了Filiform李超代数Ln，m的导子和保积Hom-结构.本文计算了一类Filiform李代数的全体Hom-结构.

文献［8］在研究幂零李代数的可约性时引进了Filiform李代数的概念.该文应用李代数的上同调理论证明了Filiform李代数构成的集合是幂零李代数簇的开子簇，这一结果对证明高维幂零李代数簇的可约性起到了至关重要的作用.文献［9］对低维Filiform李代数进行了分类，并给出了复数域上维数小于等于11的Filiform李代数的同构类.文献［10］计算了无限维Filiform李代数L1的1阶、2阶以及3阶伴随模的上同调和非等价形变.文献［11］对自然阶化拟-Filiform李代数进行了分类.文献［12］证明了任意一个n维自然阶化Filiform李代数都同构于Ln或Qn，当n是奇数时，同构于Ln，当n是偶数时，同构于Ln或Qn.本文通过计算特征零代数闭域F上有限维Z-阶化Filiform李代数Qn的齐次Hom-结构，并进一步得到了它的全体Hom-结构.

2 基本概念和性质

定义2.1［1］设（g,［−,−］）是一个李代数，φ：g→g是一个线性算子.若以下Hom-Jacobi等式成立，则称φ为李代数g的Hom-结构.若Hom-结构φ还是李代数同态，则称φ为李代数g的保积Hom-结构.

李代数g上的所有Hom-结构关于线性算子的加法和数乘构成一个向量空间，记作HS（g）.

则称李代数g是Z-阶化的.

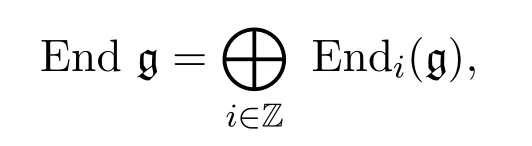
其中

若φ∈Endi（g），则称φ具有Z-次数i，记作|φ|=i.

定理2.1 设g是一个Z-阶化的有限维李代数，则有

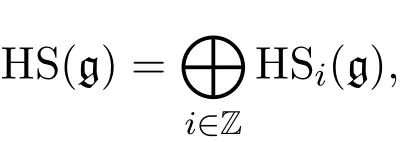
其中HSi（g）=HS（g）∩Endi（g）.

因为

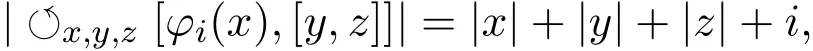
3 Filiform李代数Q n的Hom-结构

若一个n维幂零李代数的幂零指数是n−1，则称此幂零李代数为Filiform李代数.本文将计算一类比较重要的Filiform李代数Qn的Hom-结构.Qn是特征零代数闭域F上的有限维Z-阶化Filiform李代数，并且具有一组基｛X1,X2,···,Xn｝，有如下的方括号运算：

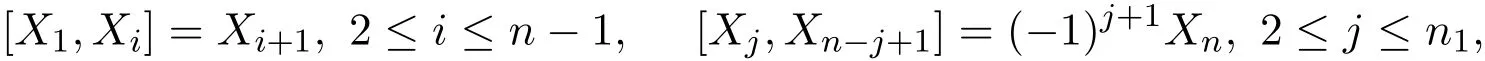
其中n=2n1,n1∈Z，其它基元素的方括号均为0.

设φ是Filiform李代数Qn的一个Hom-结构，它在基｛X1,X2,···,Xn｝下的矩阵为：

引理3.1 HS0（Qn）有一组基为：

证明 对于任意的φ0∈HS0（Qn），φ0在基｛X1,X2,···,Xn｝下的矩阵为：

由Hom-结构定义可知，φ0是Filiform李代数Qn的Hom-结构当且仅当任意基元素均满足（1）式.分如下三种情形进行讨论：

（1）取x,y,z为X1,X2,X3时，由（1）式得a12=0；

（2）取x,y,z为X1,Xi,Xn-i（2≤i≤n1−1）时，由（1）式得

（3）取x,y,z为其它基元素时，（1）式恒成立.所以，HS0（Qn）的一组基为：

引理3.2 HS2k（Qn）（1≤k≤n−2,k∈Z）有一组基如表1所示.

表1 HS2k（Q n）（1≤k≤n-2，k∈Z）的基元素

证明 对任意的φ2k∈HS2k（Qn），φ2k在基｛X1,X2,···,Xn｝下的矩阵为：

由Hom-结构定义可知，φ2k是Filiform李代数Qn的Hom-结构当且仅当任意基元素均满足（1）式.

（1）当1≤k≤n−4且为偶数时，分如下两种情况进行讨论.

（a）取x,y,z为X1,Xi,Xn-i-k（2≤i≤n1−（k+2）/2）时，由（1）式得

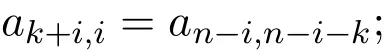
（b）取x,y,z为其它基元素时，（1）式恒成立.此时，HS2k（Qn）的一组基为：

（2）当1≤k≤n−4且为奇数时，分如下两种情况进行讨论：

（a）取x,y,z为X1,Xi,Xn-i-k（2≤i≤n1−（k+1）/2）时，由（1）式得

（b）取x,y,z为其它基元素时，（1）式恒成立.此时，HS2k（Qn）的一组基为：

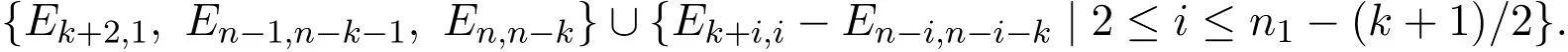
（3）当n−3≤k≤n−2时，取x,y,z为任意基元素（1）式均成立.此时，HS2k（Qn）的一组基为：｛Ek+2，1｝∪｛Ek+i，i|2≤i≤n−k｝.

（4）当k≥n−1时，φ2k=0.

引理3.3 HS-2k（Qn）（1≤k≤n−4,k∈Z）有一组基如表2所示.

表2 HS-2k（Q n）（1≤k≤n-4，k∈Z）的基元素

证明 对任意的φ-2k∈HS-2k（Qn），φ-2k在基｛X1,X2,···,Xn｝下的矩阵为：

由Hom-结构定义可知，φ-2k是Filiform李代数Qn的Hom-结构当且仅当任意基元素均满足（1）式.

（1）当k=1时，分如下四种情况进行讨论：

（a）取x,y,z为X1,X2,X3时，由（1）式得a13=0；

（b）取x,y,z为X1,X2,Xn-1时，由（1）式得an-2，n-1=0；

（c）取x,y,z为X1,Xi,Xn-i+1（3≤i≤n1）时，由（1）式得

（d）取x,y,z为其它基元素时，（1）式恒成立.所以，HS-2（Qn）的一组基为：

（2）当2≤k≤n−4且为偶数时，分如下四种情况进行讨论：

（a）取x,y,z为X1,X2,Xk+2时，由（1）式得a1，k+2=0；

（b）取x,y,z为X1,Xi,Xn-i+k（2≤i≤k+1）时，由（1）式得an-i，n-i+k=0；

（c）取x,y,z为X1,Xi,Xn-i+k（k+2≤i≤n1+（k−2）/2）时，由（1）式得

（d）取x,y,z为其它基元素时，（1）式恒成立.所以HS-2k（Qn）的一组基为：

｛E n1+k/2，n1-k/2｝∪｛E i-k，i+E n-i，n-i+k|k+2≤i≤n1+（k−2）/2｝.

（3）当2≤k≤n−4且为奇数时，分如下四种情况进行讨论：

（a）取x,y,z为X1,X2,Xk+2时，由（1）式得a1，k+2=0；

（b）取x,y,z为X1,Xi,Xn-i+k（2≤i≤k+1）时，由（1）式得

（c）取x,y,z为X1,Xi,Xn-i+k（k+2≤i≤n1+（k−1）/2）时，由（1）式得

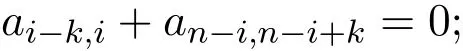
（d）取x,y,z为其它基元素时，（1）式恒成立.所以，HS-2k（Qn）的一组基为：

（4）当k≥n−3时，φ-2k=0.

定理3.1 域F上的有限维Z-阶化Filiform李代数Qn的全体Hom-结构

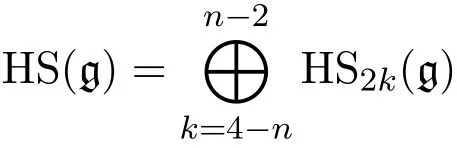
有如表3所示的一组基.

表3 HS（g）的基元素

证明 由定理2.1可知，HS（Qn）中的任意元素都可以写成齐次Hom-结构的线性组合.再由引理3.1-引理3.3可知，HS（Qn）的所有齐次分支HS2k（Qn）的基元素如上表所示，显然它们都是线性无关的，故上表所示元素的全体构成了HS（Qn）的一组基.

［1］Haryw ig J，Larsson D，Silvestrov S.Deform ations of Lie algebras usingσ-derivations［J］.J.A lgebra，2006，295：314-361.

［2］Amm ar F，Ejbehi Z，M akhlou f A.Cohom ology and deform ations of Hom-algebras［J］.J.Lie Theory，2011，21：813-836.

［3］Sheng Y.Representations of Hom-Lie algebras［J］.J.A lgebra，2012，15（6）：1081-1098.

［4］Jin Q，Li X.Hom-structures on sem i-sim p le Lie algebras［J］.J.A lgebra，2008，319：1398-1408.

［5］Cao B，Luo L.Hom-Lie superalgebra stuctures on fnite-dim ensional sim p le Lie superalgebras［J］.J.Lie Theory，2013，23：1115-1128.

［6］Yuan J，Sun L，Liu W.Hom-Lie superalgebra structures on in fnite-dim ensional sim p le Lie superalgebras of vector f elds［J］.J.Geom.Phys.，2014，84：1-7.

［7］焦阳，刘文德.Filiform李超代数Ln,m的导子和保积Hom-结构［J］.纯粹数学与应用数学，2014，30（5）：534-542.

［10］Fialow skiA.An exam p le of form aldeform ationsof Lie algebra［J］.K luwer Academ ic Pub lishers，1998，130：375-401.

［12］Vergne M.Cohom ologie des algbres de Lie nilpotentes.App lication`a l′tude de la vari`etdes algbres de Lie nilpotentes［J］.Bull.Soc.France，1970，98：81-116.

2010 M SC：17B05

The H om-structu res on Filiform Lie algeb ras Qn

Yu Huanhuan，Liu Wende

（Departm ent of M athem atics，Harbin Norm al University，Heilongjiang 150025，China）

In this paper，we prove that a linear operator on a f nite-dim ensional Z-graded Lie algebra is a Hom-structure if and only if its homogeneous com ponents are Hom-structures.We also com pute homogeneous Hom-structures on a fnite dim ensional Z-graded Filiform Lie algebra Qnover an algebraically closed f eld of characteristic zero.As a consequence，we determ ine all the Hom-structures on Qn.

Filiform Lie algebra，graded structure，Hom-structure

O 151.2

A

1008-5513（2015）02-0156-08

2014-12-23.

国家自然科学基金（11171055，11471090）；黑龙江省杰出青年基金（JC201004）.

于欢欢（1990-），女，硕士生，研究方向：李代数与李超代数.

刘文德（1965-），博士，教授，研究方向：李代数与李超代数.