非齐次树上非齐次马氏链的若干强大数定律

金少华，任梦，孙赛赛，韩瑞泽

（河北工业大学理学院，天津 300401）

非齐次树上非齐次马氏链的若干强大数定律

金少华，任梦，孙赛赛，韩瑞泽

（河北工业大学理学院，天津 300401）

通过构造适当的非负鞅，将Doob鞅收敛定理应用于几乎处处收敛的研究，给出了一类非齐次树上m重连续状态非齐次马氏链的若干强大数定律，推广了相关结果.

非齐次树；鞅；马氏链；强大数定律

DO I：10.3969/j.issn.1008-5513.2015.02.001

1 引言

树指标随机过程已成为近年发展起来的概率论的研究方向之一.强大数定律一直是国际概率论界研究的中心课题之一.文献［1］给出了Bethe树上非齐次马尔科夫随机场的一类强偏差定理.文献［2］给出了一类非齐次树上连续状态马氏泛函的若干强大数定律.文献［3］给出了非齐次树上马氏信源的一类Shannon-M cM illan定理.文献［4］研究了Cayley树指标有限状态非齐次Markov链的强大数定律和渐近均分割性（AEP）.文献［5］首先给出了在可列状态空间取值的二叉树上分枝马氏链定义的离散形式，然后建立了二叉树上分枝马氏链的若干强极限定理，最后研究了二叉树上有限状态分枝马氏链的强大数定理.文献［6］研究了m根Cayley树指标m阶有限状态非齐次M arkov链的一些极限性质.本文通过构造适当的非负鞅，将Doob鞅收敛定理应用于几乎处处收敛的研究，给出了一类m重连续状态非齐次马氏链的若干强大数定律.

2 定义

设T是一个具有根顶点o的无限树，｛Nn,n≥1｝是一列正整数集，如果第n（n≥0）层上的每个顶点均与第n+1层上的Nn+1个顶点相邻，则称T为广义Bethe树或广义Cayley树.特别地，若对非负整数集N，用模m的同余关系对其分类得到模m的剩余类，

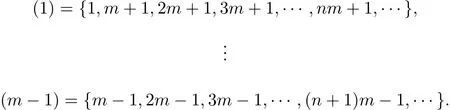
当n∈（i）时，令Nn+1=αi（αi均为正整数且不同时为1），i=0,1,2,···,m−1，就得到了一类特殊的非齐次树Tα0，α1，··，αm-1.

以下恒以T表示树Tα0，α1，··，αm-1，以Ln表示第n（n≥0）层上所有顶点的子图，Tn表示含有从顶点o到第n层上所有顶点的子图.S（t）表示顶点t的所有子代的子图.

是｛Xσ,σ∈T｝的初始分布，并有正则条件概率族：

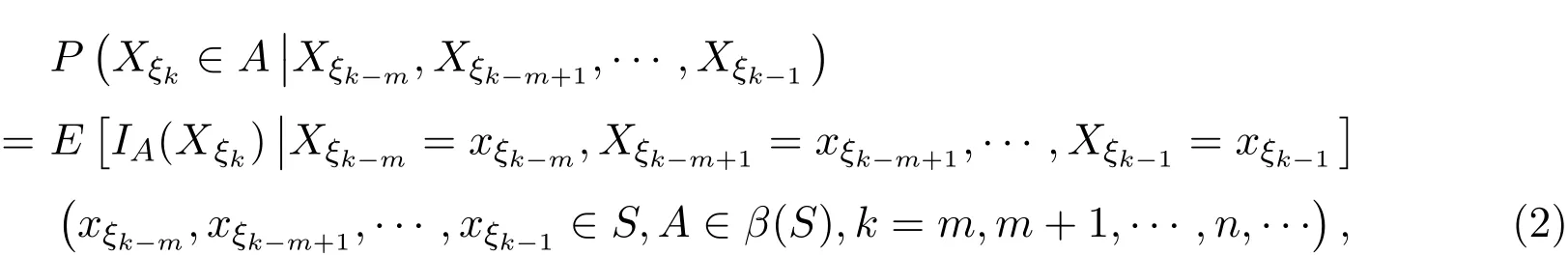
则称｛Xσ,σ∈T｝为具有初始分布（1）与正则条件概率族（2）的在S上取值的连续状态树指标m重非齐次马尔可夫链.若

则

令

也即

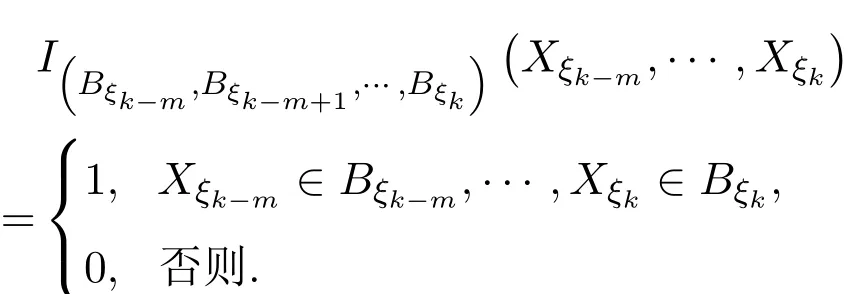
由定义2.1知，上述树T上的m重非齐次马尔可夫链的联合分布密度为：

设Q为F上的另一概率测度，设｛Xσ,σ∈T｝在Q下的联合分布密度为：

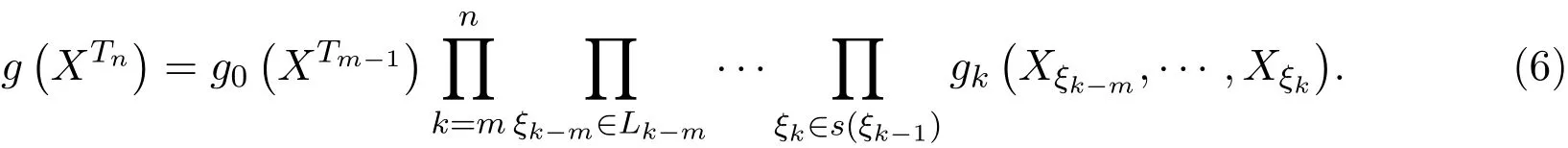
令

称rn（ω）为似然比，其中ω为样本点.令

（约定ln 0=−∞），r（ω）称为渐近对数似然比.易知，如果

则r（ω）≡0.故r（ω）可以作为n→∞时，｛Xσ,σ∈T｝在P测度下的联合分布密度f(XTn)与Q测度下的联合分布密度g(XTn)之间偏差的一种度量，r（ω）越小，偏差越小.

3 主要结果及证明

引理 3.1 设｛Xσ,σ∈T｝为如前定义的树T上的m重连续状态非齐次马尔可夫链.设

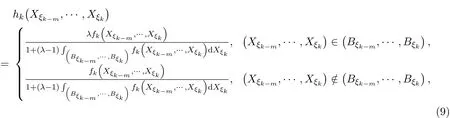
设

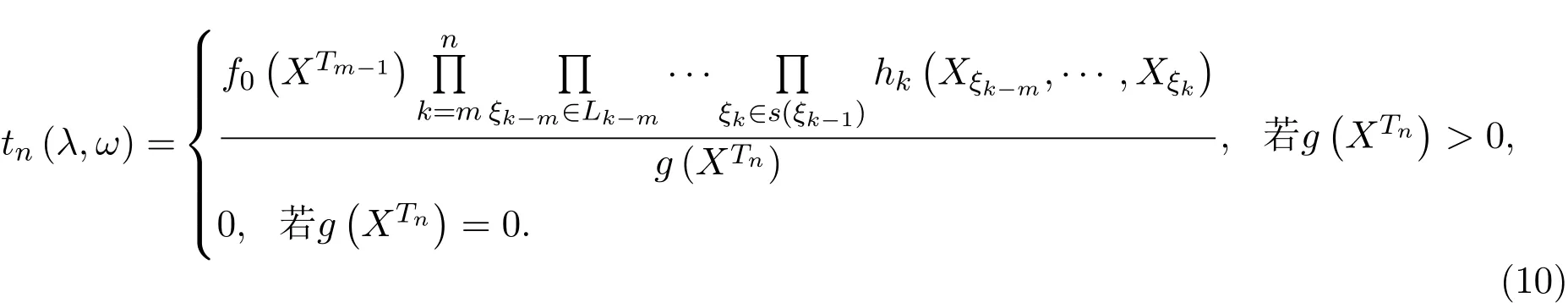
则{tn（λ,ω）,σ(XTn),n≥1}在测度Q下是一非负鞅.

证明 由

又因为

令

则

（13）式成为

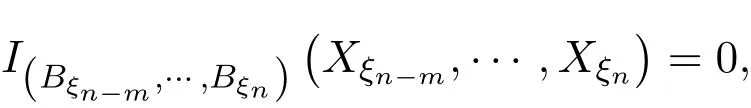
（13）式成为

故

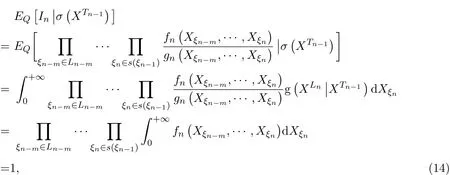
因此

定理 3.1 设 ｛Xσ,σ∈T｝为如前定义的树 T上的 m重连续状态非齐次马尔可夫链，rn（ω）和r（ω）均如前定义.设

则当0≤c≤1时，有

证明 由引理3.1及Doob鞅收敛定理知，存在A（λ）∈F，P（A（λ））=1，使得

由（9）式，有

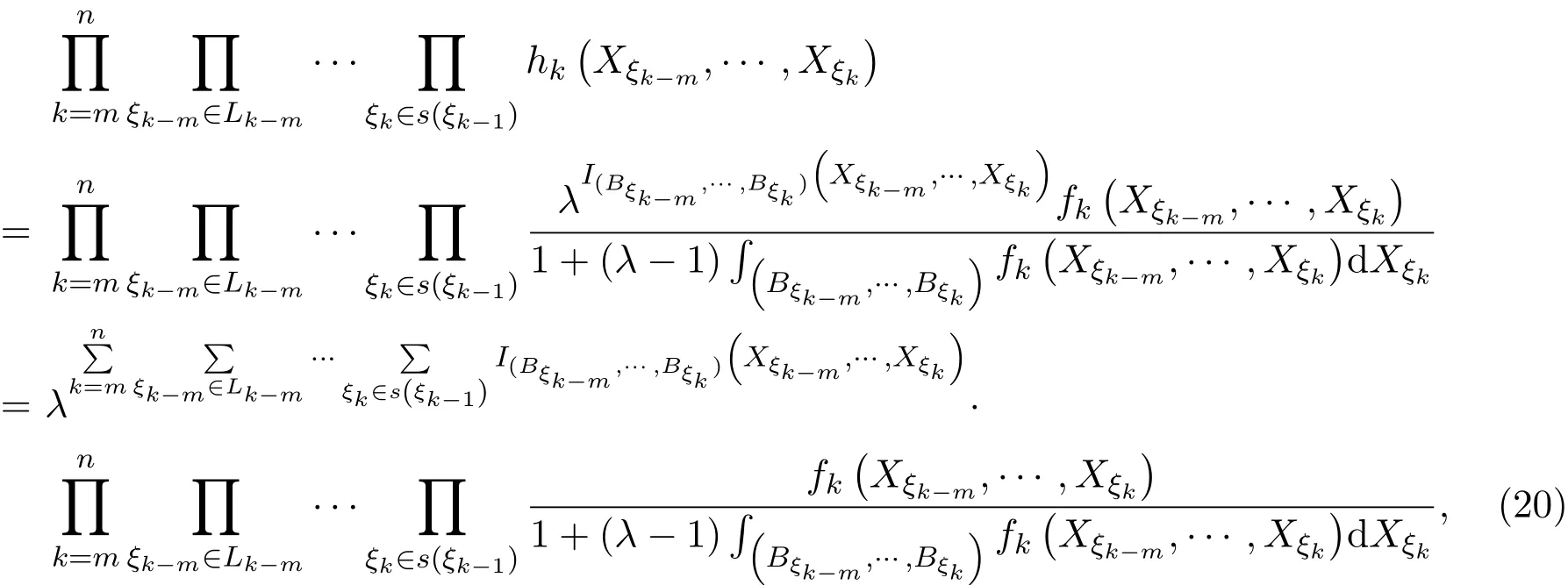
由（10）式、（19）式与（20）式，有

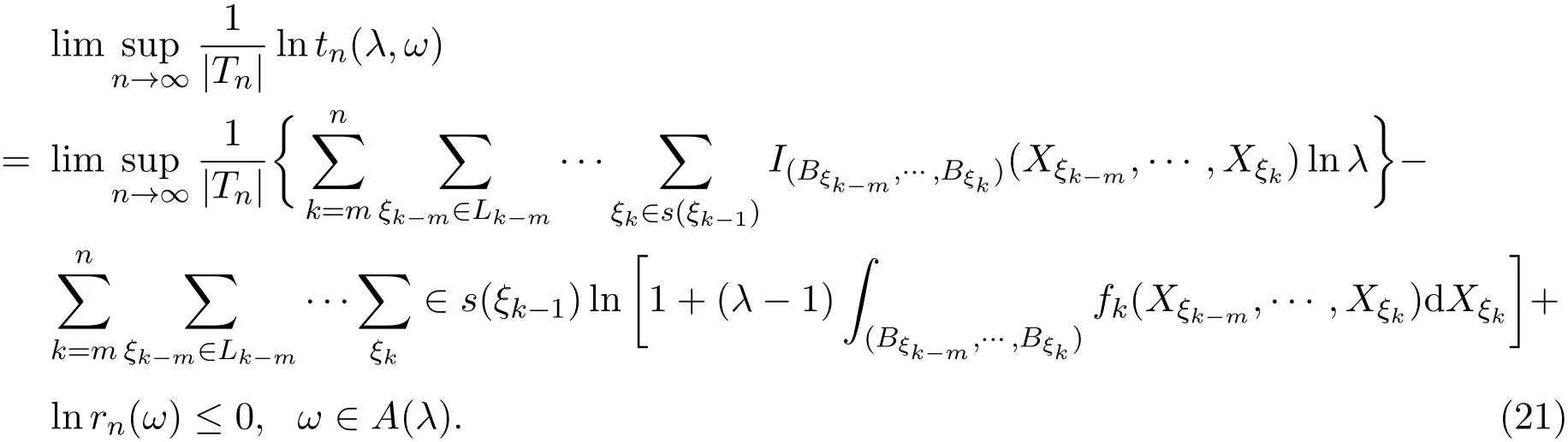
取λ＞1，将（21）式两端同除以lnλ，有

由（8）式与（22）式，有

由（16）式与（23）式，有

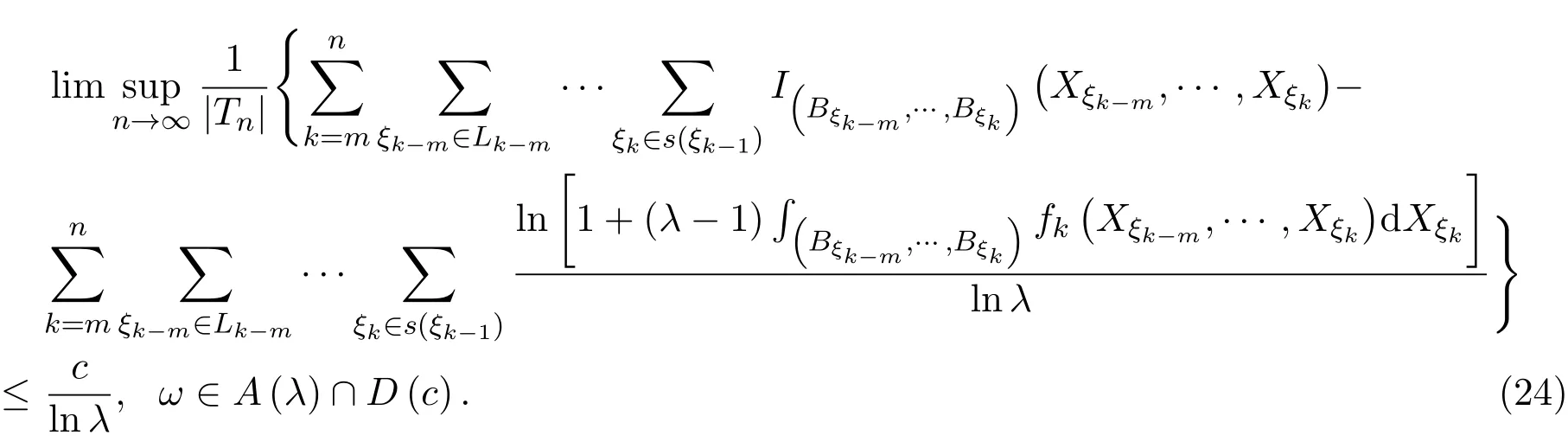
由（15）式、（24）式及上极限的性质，可得

与不等式

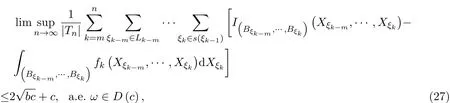
因为P（A∗）=1，故由（27）式及（28）式知（17）式成立.

当0＜λ＜1时，将（21）式两端同除以lnλ，有

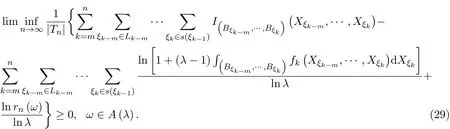
由（8）式、（16）式与（29）式，有

由（15）式、（30）式与下极限的性质，有

及不等式

则

又因为P（A∗）=1，则由（33）式及（34）式知（18）式成立.

在A1,···,Am+1中出现的次数，即

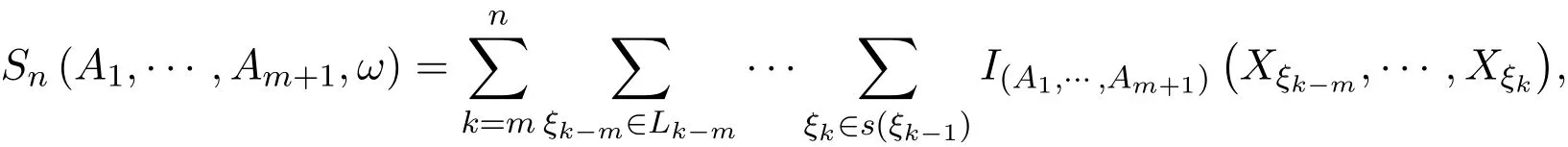
则

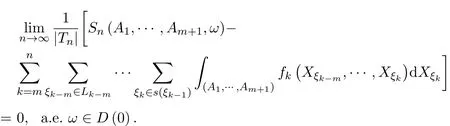
证明 在定理3.1中，令

即得推论3.1成立.

［1］Yang W G.A class of deviation theorem s for the random felds associated w ith non-homogeneous Markov chains indexed by a Bethe tree［J］.Stochastic Analysis and App lications，2012，30（2）：220-237.

［2］金少华，王东，王永生，等.关于树上连续状态马氏泛函的一类强偏差定理［J］.数学的实践与认识，2014，44（1）：212 -217.

［3］金少华，卢芳，陈秀引，等.非齐次树上马氏信源的一类Shannon-M cM illan定理［J］.纯粹数学与应用数学，2014，30（4）：331-340.

［4］Dong Y，Yang W G，Bai J F.The strong law of large numbers and the Shannon-M cM illan theorem for non-homogeneous Markov chains indexed by a Cayley tree［J］.Statist Probab.Lett.，2011，81：1883-1890.

［5］党慧，杨卫国，高荣，等.二叉树上分枝马氏链的强大数定理［J］.纯粹数学与应用数学，2013，29（5）：529-535.

［6］Shi Z Y，Yang W G.Som e lim it p roperties for them-th-order non-hom ogeneous M arkov chains indexed by an m rooted Cayley tree［J］.Statist Probab.Lett.，2010，80（15）：1223-1233.

2010 M SC：60B12

A class o f strong law s o f large num bers of non-hom ogeneous M arkov chain on a non-hom ogeneous tree

Jin Shaohua，Ren Meng，Sun Saisai，Han Ruize
（College of Science，Hebei University of Technology，Tian jin 300401，China）

In this paper，through constructing a non-negative martingale and app llying Doob′s martingale convergence theorem to the research of a.e.convergence，a class of strong law s of large numbers ofm-ordered continuous state non-hom ogeneous M arkov chain on a non-hom ogeneous tree are given.We prom ote the relative resu lts.

non-hom ogeneous tree，m artingale，M arkov chain，strong law of large numbers

O 211.4

A

1008-5513（2015）02-0111-11

2014-10-29.

河北省高等学校科学技术研究重点项目（ZD 2014051）.

金少华（1965-），博士，教授，研究方向：概率极限理论.