强阻尼非线性波动方程的解半群存在吸收集

班爱玲

强阻尼非线性波动方程的解半群存在吸收集

班爱玲

（池州学院数学与计算机学院，安徽池州247000）

无穷维动力学统在非线性科学中极为重要，而波动方程是一类重要的无穷维动力系统，本文讨论具有临界增长指数的强阻尼非线性波动方程的解所确定的解半群存在有界吸收集.

强阻尼；波动方程；吸收集

DOI：10.13420/j.cnki.jczu.2015.06.005

1　引言

设Ω是R3中的一个有界开子集，且边界∂Ω充分光滑，考虑下面波动方程的初边值问题：

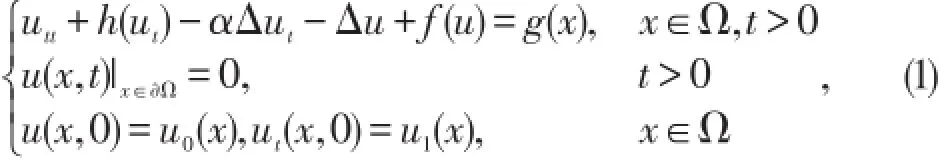
其中u=u（x，t）是Ω×［0，+∞）上的一个实值函数，α＞0称为强阻尼系数，h∈C′（R；R），g（x）∈L2（Ω），非线性项f∈C′（R；R）具有临界增长指数，且f（0）=0.

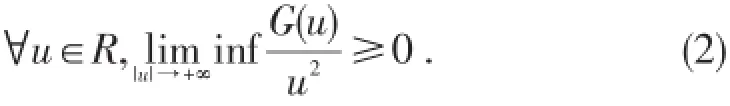
存在常数c1＞0，∀u∈R，使得

本文主要讨论系统（1）的解所确定的解半群存在一个有界吸收集.

2　预备知识

由文献［1］中的结果知，在（2）-（4）的条件下，系统（1）存在唯一的连续解u（t），满足对，系统（1）定义了一族解映射且是E上的一个连续算子半群.

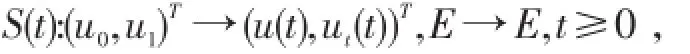
3　有界吸收集的存在性

为了下面问题研究带来方便，在E中定义一种加权内积和范数，

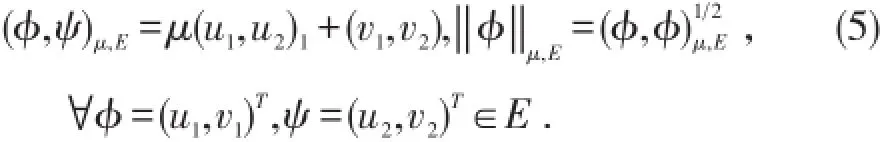
选取

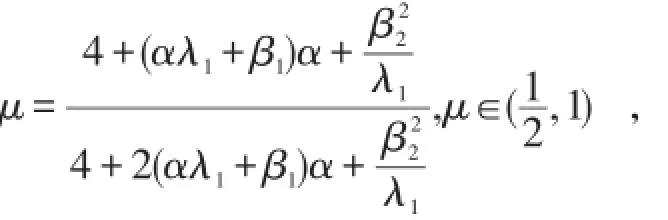
其中β1，β2是两个正常数，满足

设φ=（u，v）T，v=ut+εu，其中

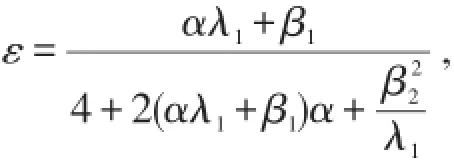
则系统（1）可以化为以下初值问题：

其中

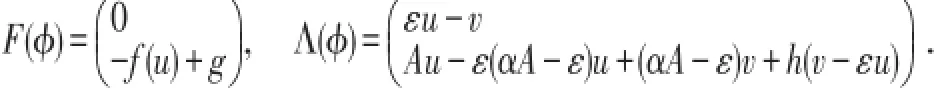
引理［3］对∀φ=（u，v）T∈E，有

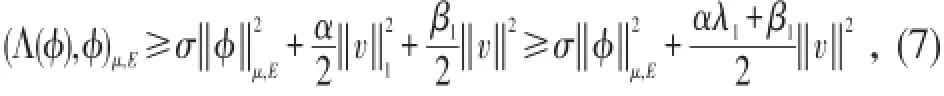
其中

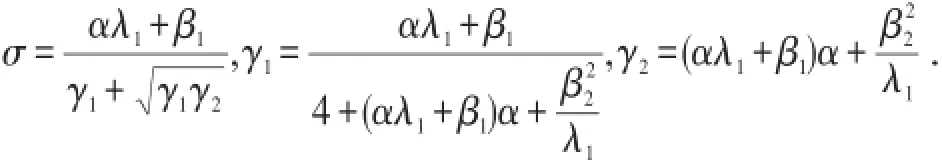
定理存在一个正常数r0＞0，对于E中的任意有界集B，存在T0（B）＞0，使得对于φ（0）∈B，系统（6）的解φ（t）=（u（t），v（t）T，满足：证明：设，用φ=（u，v）T与方程（6）两边作内积（·，·）μ，E得，

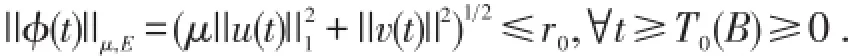
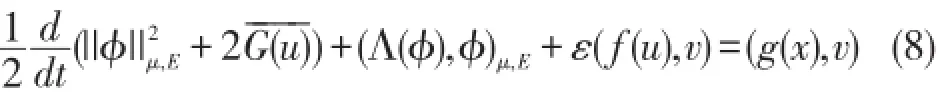
由条件（2），（3）得，

存在两个正常数l1，l2≥0，使得

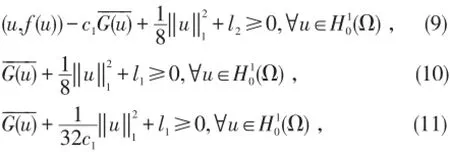
由（7），（9），（11）得，

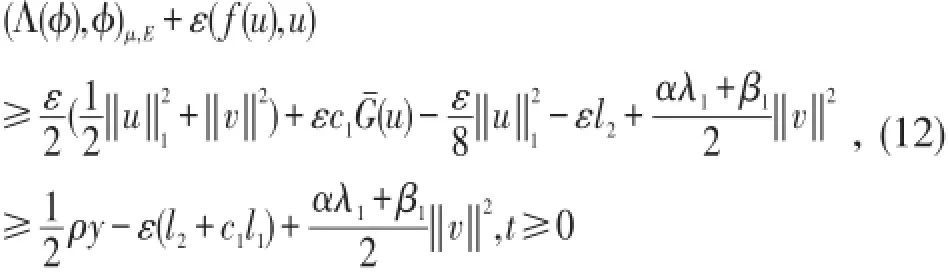
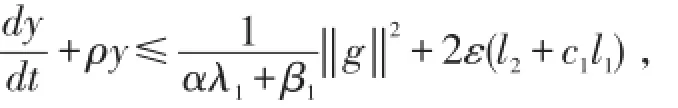
由Gronwall不等式得，

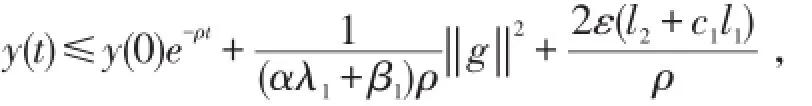
因此，有

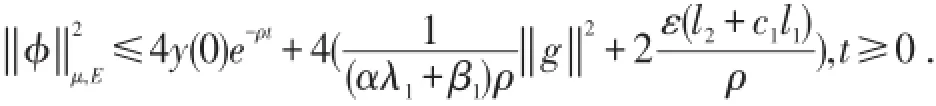
由（4）知，存在正常数c3，使得

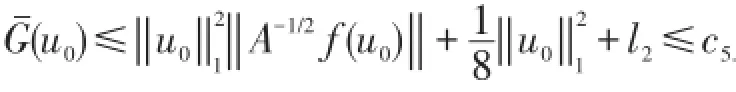
因此，存在c6=c6（r），使得

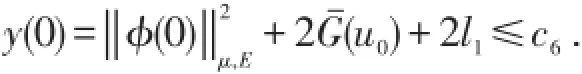
因而系统（6）的解φ（t）=（u（t），v（t）T，φ（0）∈B满足：

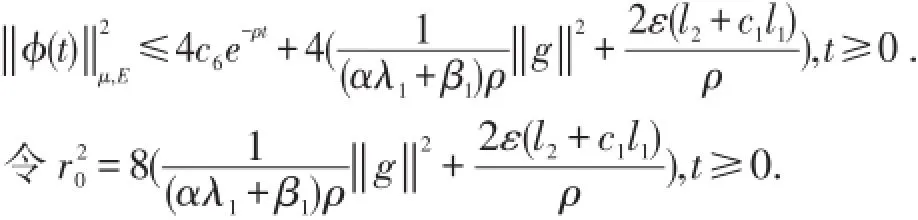
定理得证.

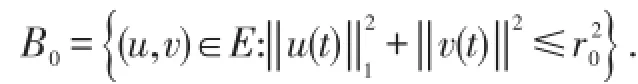
［1］Carvalho A N and Cholewa J W.Local well posedness for strongly damped wave equation with critical nonlinearities［J］.Bull. Austral.Math.Soc.，2002，66：443-463.

［2］Temam.R，Infinite-dimensional Dynamical Systema in Mechanics and Physics［M］//Appl.Math.Sciences 6.2nd Edition.New York：Springer-Verlag，1997.

［3］Zhou S F.Global attractor for strongly damped nonlinear wave equations［J］.Functional Differential Equations，1999（6）：451-470.

［责任编辑：桂传友］

O175

A

1674-1102（2015）06-0017-02

2015-03-23

池州学院自然科学研究项目（2013ZRZ006）。

班爱玲（1982-），女，安徽巢湖人，池州学院数学与计算机学院讲师，研究方向为微分方程与动力系统。