基于子带谱熵的二阶CMN语音识别鲁棒性研究

谢杨梅，吕　钊

基于子带谱熵的二阶CMN语音识别鲁棒性研究

谢杨梅1，吕钊2

（1.池州学院数学与计算机学院，安徽池州247000；2.安徽大学计算智能与信号处理教育部重点实验室，安徽合肥230039）

在自动语音识别系统（ASR）中鲁棒性是一个至关重要的问题，为了抑制训练和测试环境的失配，降低背景噪声和信道传输对语音信号的影响，文章提出了一种基于子带谱熵的二阶CMN语音识别算法。该算法利用子带谱熵在低信噪比下对语音信号进行端点检测具有较高稳健性的特点，将带噪语音分割为背景噪声段和语音信号段，为抑制噪声和信道对语音识别系统的干扰，采用在不同的区间去除各自的倒谱平均值来实现。仿真实验结果表明，该算法克服了传统CMN算法不能处理环境噪声及传输信道对语音信号所产生的非线性畸变的缺点，有效提高了语音识别系统的鲁棒性。

子带谱熵；二阶倒谱平均归正；语音识别；鲁棒性

DOI：10.13420/j.cnki.jczu.2015.06.008

1　引言

在安静的实验环境下，语音识别系统已经达到了很高的识别水平，但在真实环境下，总是伴有噪声和信道的干扰。因此，必然会引起系统性能的下降［1-3］。为了改善语音识别系统的鲁棒性，Atal提出在句子中减去长时的倒谱均值的方法以去除信道的影响，将每一帧信号的倒谱系数都减去畸变语音信号倒谱参数的平均值，是目前采用比较多的一种算法，也被认为是一种标准的信道特征补偿算法［4］。但在实际操作中，信道及噪声对语音信号产生的往往是非线性畸变，传统的倒谱归正算法不能取得理想的去噪效果。因此文章提出了一种基于子带谱熵的二阶倒谱平均归正（Band-partitioning spectral Entropy Two Levels-Cepatral Mean Normalization，简写为BETL-CMN）算法，即利用子带谱熵算法在低信噪比环境下具有较高端点检测正确率的特点，实现了对语音信号和背景噪声的分段处理，通过在不同语音段上去除各自的倒谱平均值来补偿信道的影响。

2　倒谱平均归正（CMN）

倒谱平均归正是一种常用的特征增强方法［5］，其过程如下：

给定一个语音信号y（m），对其进行分帧处理后，进行短时分析可计算出倒谱特征，从而获得T个倒谱向量序列，这些矢量的平均y¯为：

倒谱平均归正方法是将每个yt矢量都减去y¯，从而获得归正后的倒谱矢量yˆt，即：

假设信号y（n）为源信号x（m）在滤波器h（m）上的响应输出。矢量h表示倒谱域上滤波器影响，则每个元素h 可表示为：

式（3）中，B表示美尔频带的个数，||H（ωk）表示h（m）在第k个频带的频率响应幅值。

我们知道，对两个时域卷积信号进行傅里叶变换后，其运算关系将会由卷积变为乘性，再通过对数运算后可变成加性运算，即：

因此样本的平均值y¯为：

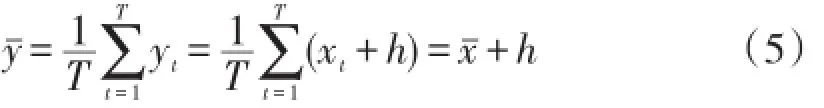
考虑式（2）、（4）和式（5），其归正的倒谱为：

通过上述分析可以看出，倒谱平均归正算法在计算发音均值时难以有效区分有声段与无声段，并且当系统中噪声与信道干扰不能被近似成为线性模型时，其有效性将会受到较大影响。为了解决这一问题，基于子带谱熵的二阶倒谱归正（BETLCMN）算法被提出了。

3　BETL-CMN算法分析

3.1噪声及信道对语音信号倒谱的影响

通常，在功率谱域，信道和噪声对纯净语音分别具有如下的乘性和加性影响

此处k=1，2，…，K，末尾的交叉项的均值为零，因为语音x和噪声n是相互统计独立的。虽然对每帧来说，该项都不为零，但是如果我们在一定频带范围内对它求和（例如计算美尔三角滤波器组输出能量），它的值通常比较小。所以对于美尔滤波器组输出能量，语音、噪声和信道之间的关系近似为

对上式两边同时取对数得到失真的语音对数功率谱的形式

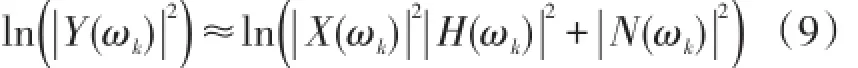
从上式中可以看出，如果在加性噪声较小的情况下，可以采用常规的CMN方法在倒谱域上抑制信道畸变对带噪语音信号的影响。然而，在噪声不能忽略的情况下，该方法在去噪时性能则表现得不尽如人意。

3.2二级CMN方法

为了处理由于信道传输及噪声对语音信号产生的非线性畸变，有人提出采用二级CMN方法［2］，对非线性通道畸变进行分段线性处理，即先将语音信号分为语音和背景两部分，并分别计算每部分倒谱矢量的平均值x¯b和x¯s，然后按式（10）计算每一帧补偿后的倒谱系数xˆt：

3.3基于子带谱熵的信号端点检测

为了实现将带噪语音划分为语音和背景两部分，首先对带噪语音信号进行分帧与加窗处理，帧重叠率为50%，在此基础上，对每帧信号进行傅里叶变换，得到每帧信号频率分量的能量谱，我们定义每个频率分量归一化谱概率密度函数为：

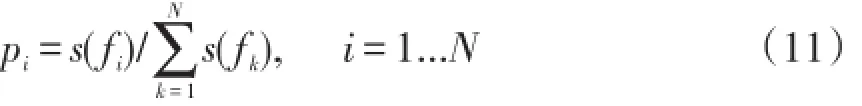
上式中s（fi）表示频率分量fi的谱能量，pi为对应的概率密度，N为傅里叶变换点数，i为待分析的某段语音帧。

因此，谱熵［6-8］被定义为：

式中H（l）是l帧语音信号的谱熵。从谱熵的性质［3，4］可知，H（l）不是谱的能量而是基于谱的能量变化，所以谱熵参数在不同水平噪声环境下具有一定的稳健性。为了进一步提高端点检测的稳健性，克服噪声对每一谱点幅值的干扰，我们将一帧分成若干个子带，再对每一子带求谱熵，即：

式中X（k，l）表示l帧语音k阶频点的幅度谱，Nb是每一帧的子带数（如：Nb=32），Eb（m，l）表示第m子带的子带能量。因此，更新后子带能量的概率为：

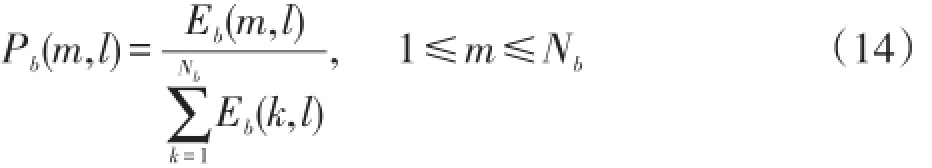
故子带谱熵［6］Hb（l）最终定义为：

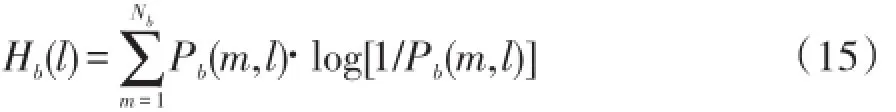
4　仿真实验与结果分析

实验采用单通道对语音信号进行采样，采样率为8KHz，采样精度为16bit，实验噪声来自于NOISEX-92数据库。实验中，我们将原始纯净语音与噪声信号按式（16）在不同信噪比下进行混合。

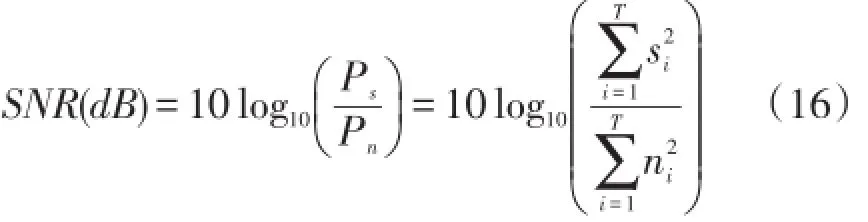
式中Ps和Pn分别表示语音信号的功率与噪声信号的功率，si和ni分别为语音和噪声信号的幅度，T是测试语音的长度。

4.1端点检测实验

实验语音采样率为8KHz，帧长设置为32ms（256个样本点），帧移为16ms（128个样本点），其内容包含来自100个讲话者的10个阿拉伯数字。图1和图2分别显示了纯净语音及SNR=-5dB时，使用子带谱熵的方法进行端点检测的波形图，红线代表语音信号的起点与终点。

图1纯净语音信号波形及使用子带谱熵进行端点检测波形

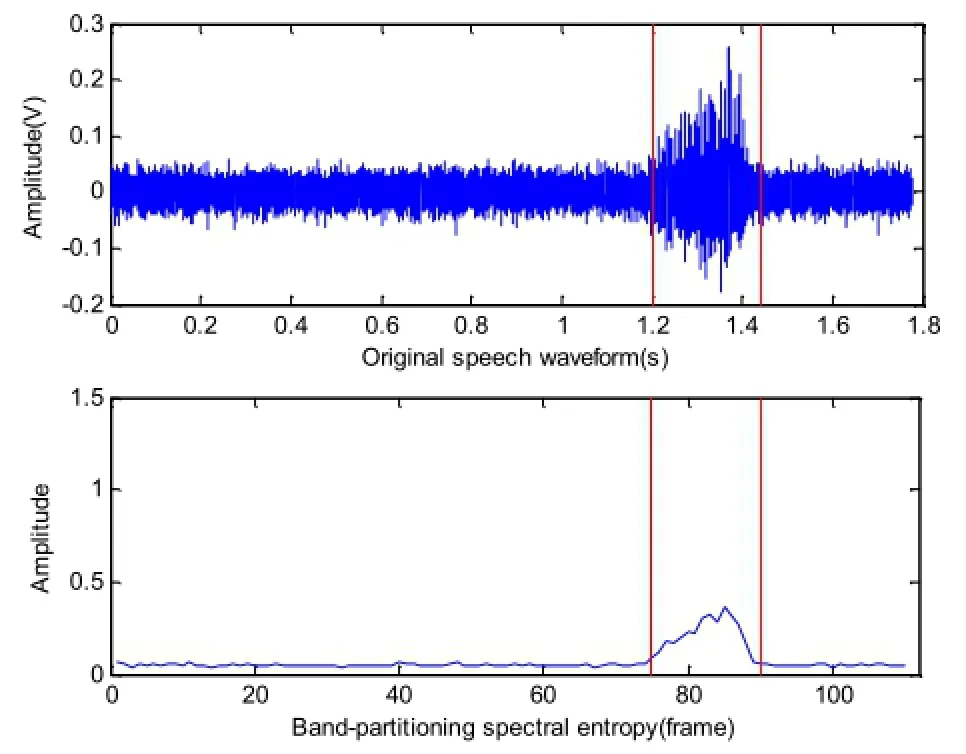
图2带噪语音波形（SNR=0dB）及使用子带谱熵进行端点检测波形

从图中可以看出，子带谱熵的方法不仅可以较好地实现对纯净语音信号的端点检测，而且在低信噪比环境下，由于谱熵是基于谱的能量变化而不是谱的能量，避免了噪声与信道所带来的对谱的能量的干扰，实现了低信噪比环境下端点检测较高的鲁棒性。

表1中ZCR/AMP表示采用传统能量/过零率算法；BSE（Band-partitioning Spectral Entropy）表示采用子带谱熵算法。上表描述了在-5dB，0dB，5dB与10dB四种信噪比较环境下，分别使用ZCR/AMP与BSE进行端点检测的实验结果。可以看出，子带谱熵的端点检测算法对不同噪声不同信噪比的情况下对系统识别相比较传统的能量/过零率算法都有明显地提高，如对于SNR=20dB的白噪声，应用传统的能量/过零率算法（ZCR/AMP）端点检测正确率为95.6%，随着信噪比的逐步降低，其检测率也随之下降，当SNR=0dB时，识别正确率降为82.5%。利用子带谱熵（BSE）算法，在SNR=20dB识别率为99.6%，较ZCR/AMP算法提高了4%，当SNR=0dB时，识别率仍保持89.9%，较ZCR/AMP算法提高了7.4%。通过计算不同噪声环境下端点检测正确率的平均值可以看出，BSE算法相比较ZCR/AMP算法，在对语音信号起点的检测上，其正确率提高约6.4%，而在终点的检测上正确率提高更大，约为10.1%。

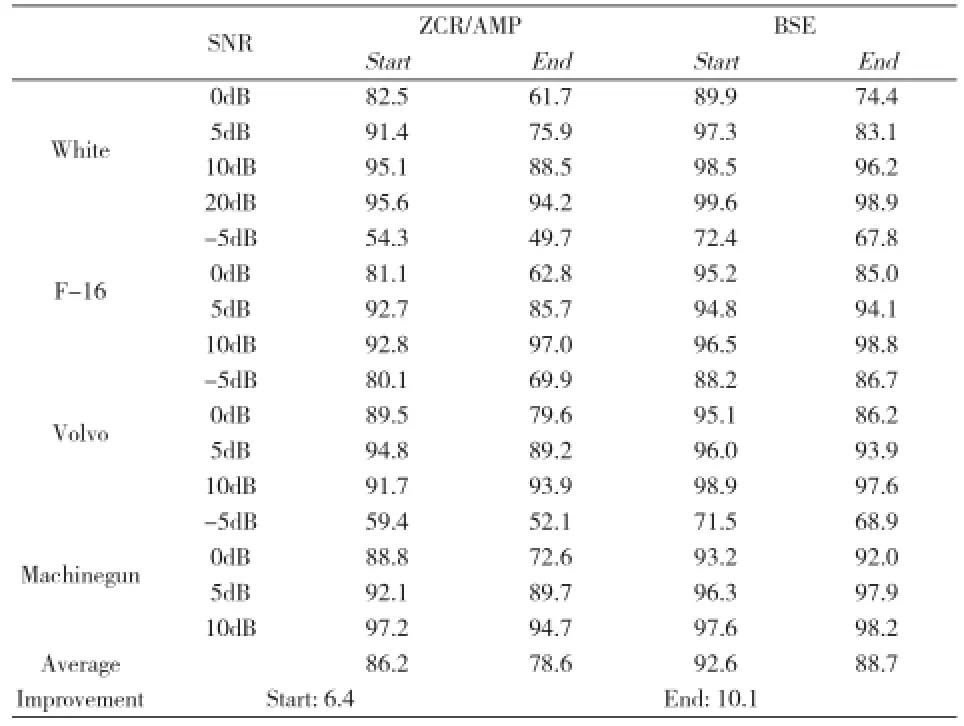
表1　语音信号端点检测正确率

传统的ZCR/AMP算法相比较BSE算法在信噪比降低时正确率下降，其原因可归结于仅使用能量与过零率难以有效区分原始语音信号的清音与摩擦音，这将导致基于ZCR/AMP方法的端点检测性能下降。而BSE算法由于计算的是基于谱能量的变化量，而不是谱能量，所以可以较好地区分出语音信号的起始点与终止点。

4.2语音识别实验

实验中所使用的语音数据库采样率为8KHz，包含来自100个讲话者的10个阿拉伯数字与10个中文单词所构成的连续语音段。其中90位讲话者用来训练非特定人语音识别模版，10位讲话者用来进行测试。为了提取MFCC特征参数，帧长同样取为32ms（256个样本点），帧移为16ms（128个样本点），并对原始语音信号进行系数为0.97的预加重和汉明窗化，以提取静态倒谱12特征参数基础上与一阶差分系数，共24维特征参数。设置最大迭代次数为Nmax=40次，结束迭代概率门限Error=5e-6。在语音库训练都收敛后，建立了10个采用自左向右的连续HMM模型参数，其中训练的状态数为6，高斯混合数是3。图3至图6分别代表了不同噪声环境下的语音识别准确率，其中，baseline表示原始带噪语音信号直接送入识别器所获取的识别精度；CMN表示采用普通倒谱归正算法时，语音识别器在识别精度；EZTL-CMN（Energy Zero-crossing Two Levels CMN）表示采用基于传统能量/过零率算法进行端点检测的二阶倒谱归正算法；BETL-CMN表示采用基于子带谱熵的二阶倒谱归正算法。

图3　白噪声下的识别精度

从实验结果中可以看出，由于CMN算法采用了对增强后语音失真和剩余噪声的补偿策略，从而改善了语音系统的识别性能，因此与基本识别系统相比，采用CMN算法的系统性能无论在何种噪声环境下都明显优于基本识别系统；基于能量/过零率的倒谱归正（EZTL-CMN）算法虽然考虑到了语音信号的非线性畸变，但是通过表1的实验结果可以看出，该算法在低信噪比环境下对语音信号的端点检测正确率不高，从而直接导致了语音识别系统正确率没有明显提高。而采用本文提出的基于子带谱熵的二阶倒谱归正算法（BETL-CMN），其语音识别性能要优于前面几种算法，并且性能的提升的程度取决于噪声的类型。比如对于白噪声、汽车噪声或飞机发动机噪声，BETL-CMN算法相比较基线系统平均提升了约40%（以SNR=5dB为例），尤其是在白噪声情况下，其识别率提升更大，从21.0%提升到79.2%，提升了58.2%，这是因为这一类噪声相对均匀地分布在整个频带上，在语音段内减去其倒谱均值后能较好地保留了原始语音信息；而对于机枪噪声，其系统提升率相对较少（仅为8.1%），原因可能是这类噪声的能量主要集中在部分频谱上，因此从频域分析来看，对语音信号形成不均匀干扰，所以在语音段内进行倒谱规正后，有可能会影响到语音信号的原始信息，从而导致识别率下降。

5　结语

图5　汽车噪声下的识别精度

为了抑制信道及噪声对语音信号产生的非线性畸变，文章提出了基于子带谱熵的二阶倒谱归正算法（BETL-CMN），该算法能在不同信噪比，尤其是在低信噪比环境下准确进行端点检测，实现语音信号与背景噪声的有效区分，然后使用传统的CMN算法对背景噪声信号进行信道补偿，以降低非线性信道畸变对语音识别系统的影响。仿真结果表明，BETL-CMN算法由于采用了分段线性模型处理方法，因此对语音信号的非线性畸变具有较好的去噪效果，同时相比较传统的CMN算法及基于能量/过零率的二阶CMN算法，语音识别系统鲁棒性得以大幅度的提升。

图6　机枪噪声下的识别精度

［1］Gerkmann T，Krawczyk-Becker M and Le Roux J.Phase processing for single-channel speech enhancement［J］.IEEE Signal Processing Magazine，2015，32（2）：55-66.

［2］何勇军，韩纪庆.语音识别中带宽失配的补偿研究［J］.计算机学报，2011，34（9）：1629-1637.

［3］夏乐乐，孙永荣，王勇.基于自适应噪声估计的语音增强技术［J］.计算机工程与应用，2014，50（23）：225-228.

［4］Atal BS.Effectiveness of linear prediction characteristics of the speech wave for automatic speaker identification and verification［J］.J Acoust Soc Am，1974，55（6）：1304-1312.

［5］Yamamoto K，Jabloun F，einhard K，et al.Robust endpoint detection for speech recognition based on discriminative feature extraction［C］//IEEE Proceedings ICASSP，2006.

［6］Wu BF and Wang KC.Robust endpoint detection algorithm based on the adaptive band-partitioning spectral entropy in adverse environments［J］.IEEE Transaction on speech and audio processing，2005，13（5）：762-775.

［7］侯周国，钱盛友，姚畅.短时域语音端点检测中谱熵算法的改进［J］.计算机工程与应用，2006，42（21）：55-56.

［8］Misra H，Martigny S，Ikbal S，et al.Multi-resolution spectral entropy feature for robust ASR［C］//IEEE Proceedings ICASSP，2005.

［责任编辑：桂传友］

TN912

A

1674-1102（2015）06-0023-04

2015-09-24

安徽高校省级优秀青年人才基金项目（2011SQRL162）；池州学院自然科学科研项目（2010ZR010）。

谢杨梅（1979-），女，安徽池州人，池州学院数学与计算机学院讲师，硕士，研究方向为智能信息处理，吕钊（1979-），男，安徽宿州人，安徽大学计算机科学与技术学院副教授，博士，研究方向为智能信息处理与人机交互技术。