某类解析函数的Fekete-Szego¨不等式

宋　园，郭　栋

某类解析函数的Fekete-Szego¨不等式

宋园，郭栋

（滁州职业技术学院基础部，安徽滁州239000）

研究了正规化解析函数H的子类N（β，λ，α）的Fekete-Szego¨不等式，对于任意的f（z）=z+a2z2+a3z3+···∈N（β，λ，α）及任意的复参数μ，应用正实部函数的，得到了的精确上界.

N（β，λ，α）函数；从属；Fekete-Szego¨不等式

DOI：10.13420/j.cnki.jczu.2015.06.006

1　引言

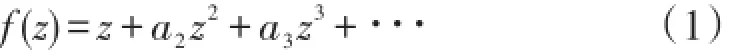
设f（z）和F（z）都在U内解析.若存在U内满足||ω（z）≤||z的解析函数ω（z），使得f（z）≡F（ω（z），则称f（z）从属于F（z），记作f（z）≺F（ω（z）.

于1933年证明了如下结果Fekete和Szego¨［1］。

定理A设f（z）∈S，f（z）由（1）式给出，0≤μ＜1则

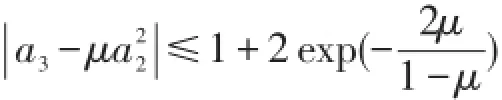
且对每个μ等号都成立.

定义：令0＜λ＜1，β∈C，α＜1，定义

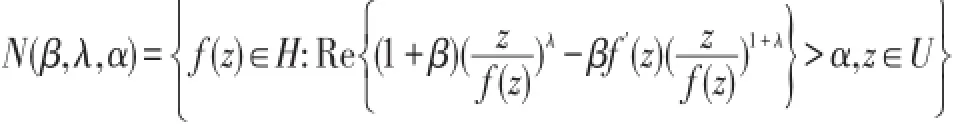
其中的幂指数取主值。

此函数类是文献［2］中引入的解析函数类，显然N（-1，λ，0）是文献［3］中讨论的non-Bazileviv函数类.

一些作者［4-7］对于S或H的某些子类讨论了它们的Fekete-Szego¨问题。文献［6］研究了N（β，λ，α）的Fekete-Szego¨不等式，本文用不同于文献［6］的方法研究N（β，λ，α）的Fekete-Szego¨问题，该结果包含了文献［3］中的一些结论.

为了导出我们的主要结果，我们需要如下引理。

引理1.1［7］如果p（z）=1+c1z+c2z2+···是内具有正实部的解析函数，则对任意的复数ν，有.等号在函数或者时成立.

引理1.2［8］如果p（z）=1+c1z+c2z2+···是内具有正实部的解析函数，则对任意的实数ν，有

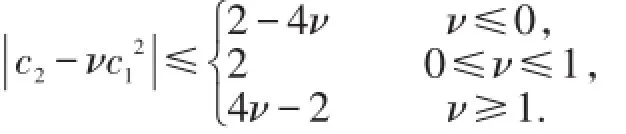
2　主要结果及证明

定理2.1设f（z）由（1）式给出，f（z）∈N（β，λ，α），μ为复数，则

且对所有的μ等号都能成立.

证明：因为f（z）∈N（β，λ，α），所以存在p（z）=1+p1z+p2z2+···∈P，使得

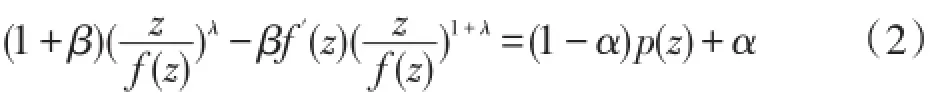
将f（z），p（z）的幂级数展开式代入（2）式，并比较恒等式两边的z和z2两项的系数，可得

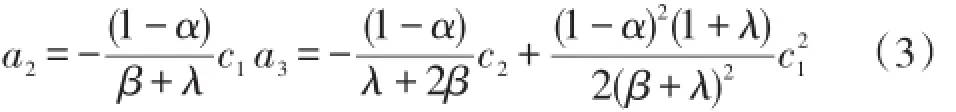
所以

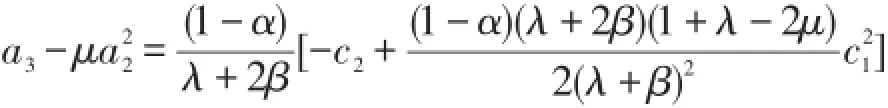
因此：

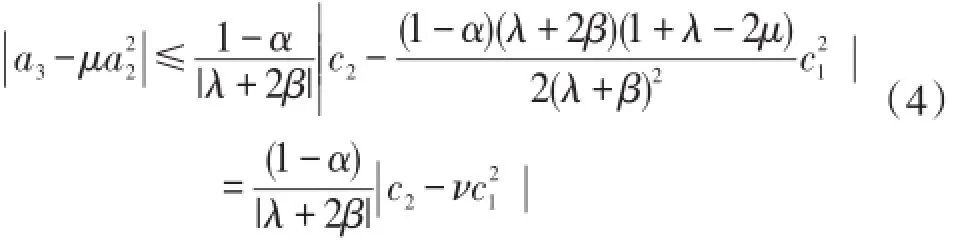
1.1可得定理2.1，

（1）λ≠0时相应的极值函数为：

（2）λ=0时相应的极值函数满足：

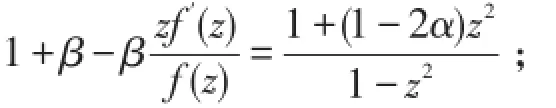
注释：定理1.1就是文［6］中的定理1，不过证明方法简单多了.

由式（4）及引理1.2我们可得下面的定理2.2：定理2.2设f（z）由（1）式给出，f（z）∈N（β，λ，α），β≥0，μ为实数则

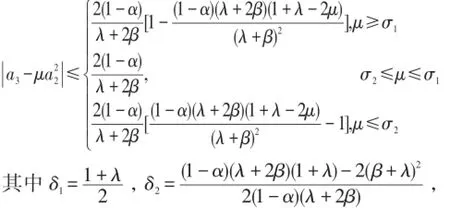
且对所有的μ等号都能成立。

类似于定理2.1的证明，我们可得下面的定理2.3。

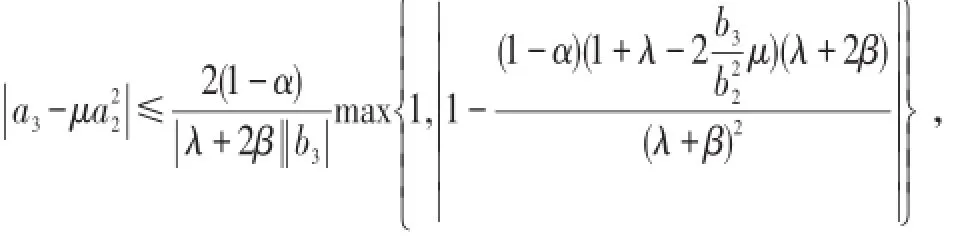
且对所有的μ等号都能成立.

由于Dn（f）=（f∗g）（z）∈N（β，λ，α），其中b2=n，b3=n（n+1）则由定理2.3可得：

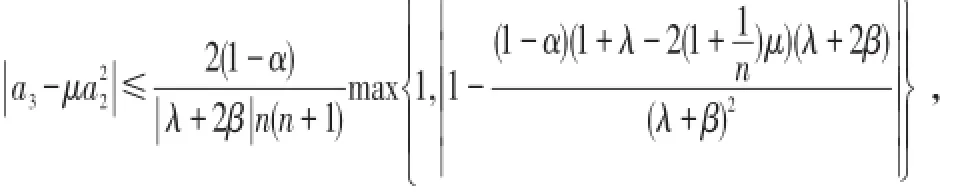
且对所有的μ等号都能成立。

［1］Fekete M，SzegO¨G.Eine Bermerkung uberungerade schlichte funktionen［J］.J London Math Soc，1933，（8）：85-89.

［2］Wang Zhigang，Liao Mao xin.On certain generalized class of non-bazilevicˇfunctions［J］.Mathematica Academiae Paedagogicae Nyiregyhaziensis.2005，21：147-154.

［3］Nikola Tuneski，Maslina Darus.Fekete-szego¨functional for nonbazilevCˇfunctions［J］.Acta Mathematica Academiae Paedagogicae Nyiregyhaziensis.2002（18）：63-65.

［4］郭栋，刘名生.关于解析函数类的Fekete-Szego¨问题［J］.华南师范大学学报：自然科学版，2007（2）：33-38.

［5］郭栋，李宗涛，杨家稳.一类解析函数类的Fekete-Szego¨问题［J］.华南师范大学学报：自然科学版，2012，44（4）：32-34.

［6］郭栋，李宗涛.某类解析函数的Fekete-Szego¨不等式［J］.江汉大学学报：自然科学版，2012，40（1）：8-9.

［7］Ravichandran V，Metin Bolcal，Yasar Polatoglu，Sen A.Certain subclasses of starlike and convex functions of complex order［J］. Hacettepe Journal of Mathematics and Statistics，2005，34：9-15.

［8］周从会.γ-星函数类的Fekete-Szego¨不等式［J］.安徽理工大学学报：自然科学版2010，30（2）：75-78.

［责任编辑：桂传友］

O174

A

1674-1102（2015）06-0019-02

2015-01-23

安徽高校自然科学重点研究项目（KJ2015A372）。

宋园（1982-），女，安徽滁州人，滁州职业技术学院基础部讲师，硕士，主要研究方向为矩阵理论。