一类奇异摄动反应扩散方程数值模拟中的参数估计

包小兵，陈振荣

一类奇异摄动反应扩散方程数值模拟中的参数估计

包小兵，陈振荣

（池州学院数学与计算机学院，安徽池州247000）

针对一类奇异摄动反应扩散方程，使用Shishkin网格方法进行求解，其中的网格过渡点参数较难确定，使用粒子群（PSO）算法估计存在计算速度慢的缺点，提出了基于差分进化（DE）算法的过渡点参数估计。通过具体的数值实验，结果表明：与PSO算法相比，计算精度相当，计算速度明显提高，说明所提方法的可行性与有效性。

奇异摄动反应扩散方程；Shishkin网格；粒子群算法；差分进化算法

DOI：10.13420/j.cnki.jczu.2015.06.007

本文考虑如下的奇异摄动反应扩散方程：

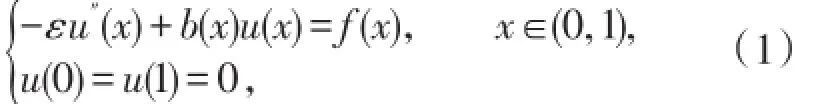
其中0＜ε＜＜1，函数b（x）和f（x）是充分光滑的，且b（x）≥β＞0。众所周知，当ε→0时，问题（1）的精确解在区间［0，1］的两端存在边界层。

对于奇异摄动问题（1），一些常用的数值方法很难得到理想的数值结果。因此，Shishkin网格方法和Bakhalov网格方法，越来越被广泛地用来数值求解上述奇异摄动反应扩散方程（1），见文［1-3］。

众所周知，差分进化算法［5］（简称DE）它已被广泛应用到各种参数估计的求解，见文［6-9］。考虑到差分进化算法具有较快的收敛速度，本文在文［4］的基础上，利用DE算法对Shishkin网格参数进行优化计算，并与粒子群算法的计算结果进行比较和分析。

1　Shishkin网格的构造与离散格式的建立

为了建立问题（1）的迎风差分格式，首先构造出Shishkin网格。

设Shishkin网格过渡点为：

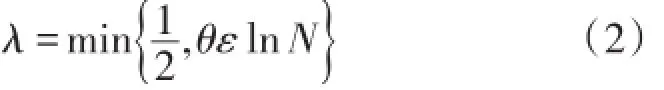
其中N为对网格的剖分数，且为4的倍数，θ为待确定的参数，我们首先将区间分成三个子区间］，然后对区间进行等分，分别对区间进行

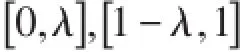
N 4等分，则网格可记为：

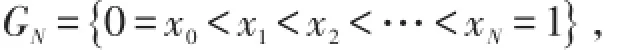
其网格步长为：

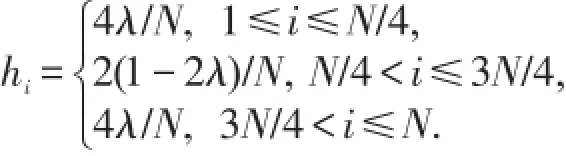
基于以上网格GN，可建立如下迎风差分格式

其中Ui为u（xi）的近似解，

2　基于差分进化算法的Shishkin网格参数估计

由区间［0，1］上的N+1个点构成网格GN

再对网格GN加密一倍得到网格G2N：

我们知道，微分方程数值解的误差可用如下式子来表示

其中‖‖·为向量范数。然而，一般情况下，微分方程的精确解U*很难得到，故常用

来估计误差，其中UN（θ）为问题（1）在网格GN下的数值解，U2N（θ）为问题（1）在网格G2N下的数值解。

显然，参数θ的取值将影响到EN的大小，为使其尽可能小，构造如下的目标函数：

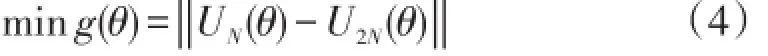
本文将使用DE算法估计出（4）式中的参数θ，然后求解方程组（3），得到问题（1）的数值解。

3　数值实验与结果分析

考虑奇异摄动反应扩散方程：

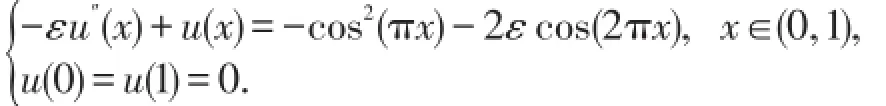
为了验证差分进化算法数值求解这类问题的优点，在相同条件下与基本粒子群算法［4］进行比较。差分进化算法的参数设置为：种群规模为40，交叉因子为0.5，交叉概率为0.1，最大迭代次数为40次。粒子群算法的参数设置为：学习因子c1=c2=1.2，粒子数为50，最大迭代次数为40次。

下面，我们分别使用PSO算法和DE算法估计参数θ，计算结果如表1、表2所示。

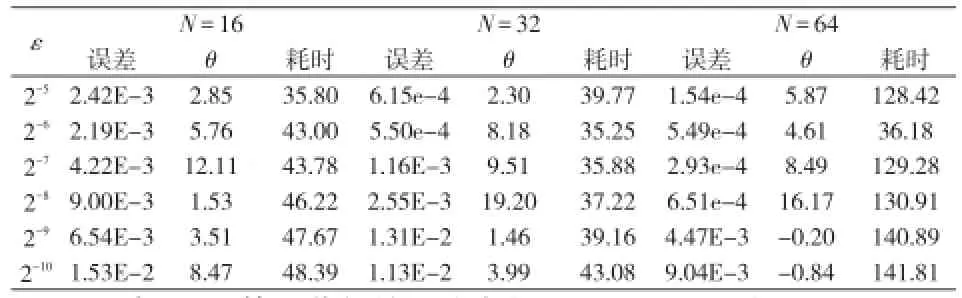
表1　PSO算法获得的网格参数、误差及耗时（单位：s）

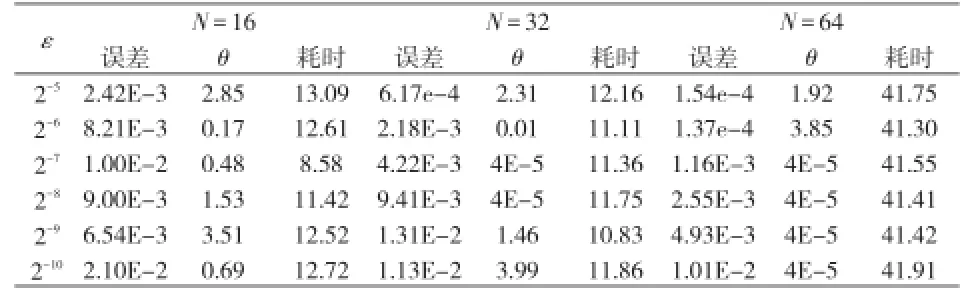
表2　 DE算法获得的网格参数、误差及耗时（单位：s）

实验表明，使用DE算法估计参数θ与使用PSO算法估计参数θ的误差相当，但计算速度明显较高。可以看出，N=16，ε=2-5、2-8、2-9时，误差和参数θ的值几乎相等，但计算耗时差异较大，由此可知本方法性能和效果较优。图1给出了N=16，ε=2-9时，PSO算法和DE算法的迭代曲线。

4　结论

对于奇异摄动问题的数值方法，目前以层适应网格方法的应用最为普遍，其中Shishkin网格方法因为结构简单而备受关注。对于奇异摄动反应扩散方程的Shishkin网格方法，本文在文［4］的基础上，提出了奇异摄动问题数值模拟中参数估计的差分进化算法，并与基本粒子群算法进行了比较，数值结果表明差分进化算法的计算效率明显优于基本粒子群算法。

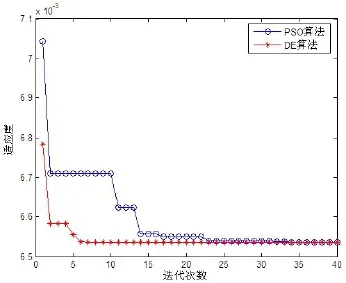
图1　N=16，ε=2-9时的迭代曲线

［1］Miller J J H，O'Riordan E，Shishkin G I.Fitted numerical methods for singularly perturbed problems［M］.Singapore：World Scientific，1996.

［2］Kumar K.High order compact finite difference scheme for singu-larly perturbed reaction diffusion problems on a new mesh of Shishkin type［J］.Journal of Optimization Theory and Applications，2009，143（1）：123-147.

［3］Lin T，Radojev G，Zarin H.Approximation of singularly perturbed reaction-diffusion problems by quadratic C1splines［J］.Numerical Algorithm，2012，61（1）：35-55.

［4］刘利斌，欧阳艾嘉.奇异摄动反应扩散方程数值模拟的粒子群优化算法［J］.计算机应用，2014，34（4）：1080-1082，1093.

［5］Srorn R，Price，K.Differential evolution：a simple and efficient adaptive scheme for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11（4）：341-359.

［6］王钧炎，黄德先.基于混合差分进化算法的混沌系数参数估计［J］.物理学报，2008，57（5）：2755-2760.

［7］王海伦，余世明，郑秀莲.自适应差分进化算法及其在参数估计中的应用［J］.计算机工程，2012，38（5）：202-204.

［8］熊伟丽，陈敏芳，张乾，等.基于改进差分进行算法的非线性系统模型参数辨识［J］.计算机应用研究，2014，31（1）：124-127.

［9］朱大艺，陈少清，欧忠辉.差异演化算法在土壤分形维数估计中的应用［J］.土壤通报，2013，44（5）：1081-1085.

［责任编辑：桂传友］

TP18

A

1674-1102（2015）06-0021-02

2015-03-02

池州学院自然科学研究项目（2014ZR005）；安徽省大学生创新项目（AH201411306088）；全国大学生创新创业训练计划项目（201511306034）。

包小兵（1981-），男，安徽庐江人，池州学院数学与计算机学院讲师，硕士，研究方向为智能计算。