基于连续差联合阵列的非等距线阵无模糊波束形成方法

黄 岩廖桂生 李 军 李 婕

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

基于连续差联合阵列的非等距线阵无模糊波束形成方法

黄 岩*廖桂生 李 军 李 婕

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

该文针对非等距线阵波束形成产生栅瓣的问题，提出一种基于连续差联合阵列的非等距线阵无模糊波束形成方法。该方法基于连续差联合阵列对非等距线阵进行阵形优化分析，利用连续差联合阵列与连续波程差一一对应的特性，扩展得到非等距线阵Toeplitz化的协方差矩阵。根据线性约束最小方差（LCMV）准则，可以直接利用该协方差矩阵得到稳健自适应波束形成。由于重构的协方差矩阵与相同孔径等距线阵的协方差矩阵相似，不会产生相位模糊，避免了波束形成栅瓣的影响。大量的仿真实验证明了该文方法的稳健性能。

信号处理；差联合阵列；非等距线阵；无模糊波束形成

1 引言

波束形成方法一直是阵列信号处理研究的热点问题，对期望目标方向功率增强的同时自适应抑制干扰方向的波束一直是雷达的目标和期望。阵列信号波束形成分为发射波束形成和接收波束形成，发射波束形成通过数字信号加权来形成波束指向并确认目标的方位范围［1-3］，而接收波束形成则在接收端形成虚拟波束，可以积累多次快拍并利用超分辨方法捕获目标的精确方位［4-8］。

对于等距线阵来说，如果阵元间距小于半波长，则协方差矩阵中产生的波程差变化范围就不会超出2π，即不会产生2π相位模糊。而N个阵元的等距线阵可用的空间自由度为 N-1，即最多可以抑制的干扰数为 N-1。在阵元数固定的情况下，实际情况中，为了节约天线成本，现在逐渐考虑利用稀疏布阵的非等距线阵来扩展阵列孔径，提高可用自由度。然而，由于阵列稀疏布阵，阵元间距可能会大于半波长，这时形成协方差矩阵中产生的波程差变化范围会超出2π，产生2π相位模糊，由此会带来严重的栅瓣现象，导致目标方向能量无法聚集和栅瓣干扰能量较强等问题的出现。同时接收的信号有效快拍数较少，快拍数也极大地限制了接收波束形成的效果。原有的文献提出一些非等距线阵的阵形设计来避免相位模糊，文献［9］提出一种联合阵列的思想，其中差联合阵列（difference coarray）表示所有阵元相对位置之差所构成的集合；文献［10］在差联合阵列的基础上提出一种二级嵌套阵列，可以满足差联合阵列是连续的；而最小冗余阵列（MinimumRedundancy Array， MRA）的提出实际上是利用最少的阵元数得到一定长度的连续差联合阵列［11，12］。针对基于连续差联合阵列的非等距线阵，很多学者提出一些波束形成方法：文献［13］提出利用插值方法弥补缺少的阵元位置将非等距线阵转化成等距线阵，可以利用得到的等距线阵作波束形成，但是该插值方法采用最小二乘拟合时对欠定方程求解会产生误差；文献［10］提出一种基于Khatri-Rao（KR）子空间［14］的空间平滑方法，将非等距线阵的协方差矩阵向量化后，利用空间平滑方法重构信号的协方差矩阵，然而该方法只能利用非等距线阵阵元的部分信息。

为了解决上述问题，本文对非等距线阵的阵形进行优化设计并提出适用于非等距线阵的无模糊接收波束形成方法，该方法在低快拍下也有较好的波束形成效果。实际上，差联合阵列中的各个元素一一对应于协方差矩阵中能够得到的所有波程差。考虑若非等距线阵的差联合阵列是连续的，则可得到连续的波程差，就相当于得到了同等孔径等距线阵的波程差。理想情况下协方差矩阵具有Toeplitz的性质，利用得到的连续波程差可以得到扩展的非等距线阵协方差矩阵。根据线性约束最小方差（LCMV）准则，可以直接利用该协方差矩阵作最小方差无畸变响应（MVDR）自适应接收波束形成器。在实际阵列信号处理时，一般可以得到的有效快拍数较少，由于本文方法扩展的协方差矩阵具有 Toeplitz结构，故在低快拍下也能有较好的性能，大量的仿真实验验证了本文方法在低快拍条件下的有效性和稳健性。

2 信号模型

假设N个阵元的非等距线阵作为接收阵列，定义第1个阵元为参考阵元，则所有阵元的相对位置为如图1所示。假设有K个远场窄带信号分别从入射到该接收阵列。若信号的波长为λ，则第 k个信号对应的接收信号导向矢量为则接收信号导向矢量矩阵可以表示为

图1 非等距线阵示意图

假设第k个目标的反射系数为 βk，在1个脉冲重复周期（PRT）内，接收阵列得到的回波信号为

3 非等距线阵无模糊波束形成方法

首先介绍差联合阵列的概念并分析本文无模糊波束形成方法的基础。定义如下集合：其中Ar表示接收阵元的位置集合，集合D表示接收阵列中所有阵元位置之差构成的集合。由于集合 D中会有很多相同的位置差，定义集合D中所有不相同的元素构成的集合为Du，该集合即为差联合阵列（difference coarray）［9］。集合Du中的du元素在集合D中出现的次数定义为权重系数wd（du）。

差联合阵列表示了该阵列所有阵元位置差值的集合，实际上差联合阵列一一对应于该阵列可以得到的所有波程差。对于一个M阵元的等距线阵，假设其阵元间距为 d = λ/2，由式（5）可得，其协方差矩阵可以近似表示为

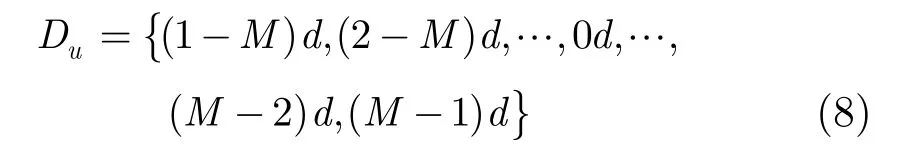
由此可见，波程差和差联合阵列是一一对应关系。若非等距线阵阵元间的相对位置能得到如式（8）所示的连续差联合阵列，则该非等距线阵的协方差矩阵中的元素就可以恢复得到表示2M - 1个不同波程差的元素，从而扩展非等距线阵的协方差矩阵。所以，非等距线阵的差联合阵列必须是连续的，该条件是本文无模糊波束形成方法的基础。实际上，该基础也是设计最小冗余阵列的约束条件。最小冗余阵列的设计原理是利用最少的阵元得到给定长度的连续差联合阵列，即求解以下优化问题：其中，L表示给定连续差联合阵列的最大值，最小冗余阵为式（9）条件下的最优非等距线阵。举个例子，假设非等距线阵阵元间的最小间距为 d = λ/2，其余阵元间距均为最小间距的整数倍。5个阵元的最小冗余阵相对阵元位置分别为｛0d，2d，5d， 8d，9d｝，根据式（8），其差联合阵列为｛-9d，-8d ，…， 0d ，…，8d，9d｝，差联合阵列的权重系数如图2所示。

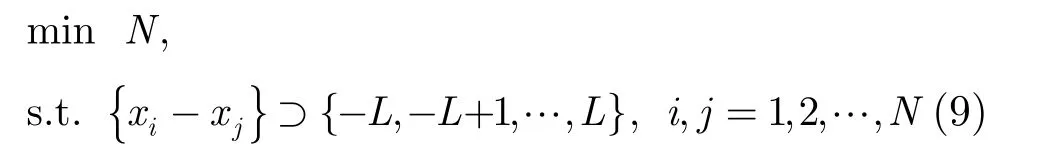
根据上述分析，本文提出一种基于连续差联合阵列的无模糊波束形成方法，其具体步骤如下：若M=xN+1，非等距线阵阵元间的相对位置能得到如式（8）所示的连续差联合阵列，则非等距线阵协方差矩阵中的元素实际上对应于式（7）中等距线阵协方差矩阵的相关元素，则可得：

对于 5个阵元的最小冗余阵，根据式（10）可得其未扩展的协方差矩阵 RYY为

图2 5个阵元最小冗余阵的差联合阵列示意图

由于M=xN+1，则非等距线阵与等距线阵的孔径相同（例如，5个阵元的最小冗余阵最后一个阵元的位置为x5=9d，则M=10）；同时式（10）中得到了该孔径下所有波程差对应的元素，那么式（10）的协方差矩阵可以扩展为一个像 RULA一样的M × M维协方差矩阵：

因为非等距线阵的差联合阵列是连续的，即能得到式（7）中全部2M - 1个波程差，则在R︿YY中每个对角线至少有1个非零元素存在，而对角线上非零元素的个数等于上文定义的权重系数 wd（du）。故YY可以被填满成一个如下Toeplitz矩阵：

其中，由于快拍数和信噪比的影响，式（11）中协方差矩阵同一波程差对角线上的非零元素不是全都相等的；Ri（du）表示对应于波程差 R（du）对角线上的第i个非零元素，这些非零元素就是扩展未填充协方差矩阵YY中的非零元素。由于故是一个正定Toeplitz矩阵。同时是一个满秩协方差矩阵，根据线性约束最小方差（LCMV）准则，故可以利用该协方差矩阵进行有效的约束作稳健 MVDR波束形成器。假设目标方向为 θ0，则MVDR波束形成器可以用下面的优化问题表示：

则式（14）中MVDR最优权向量［15］可以表示为

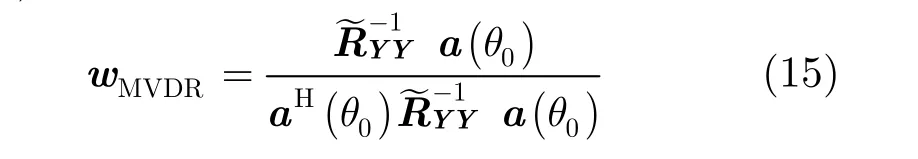
根据以上分析，就可以根据满秩协方差矩阵得到无模糊的MVDR波束形成。以上本文提出的波束形成方法与文献［7］中的基于KR子空间的空间平滑方法应用基础是相同的，但是对样本的利用上有以下不同：文献［7］中的空间平滑方法是将协方差矩阵向量化，得到差联合阵列的导向矢量再作空间平滑重构信号协方差矩阵，该方法实质上只利用了式（11）协方差矩阵对角线上的一个非零元素（即差联合阵列每个位置的一个元素），这样会损失一部分样本信息，样本冗余越多则误差越大；而本文提出的方法可以充分利用波程差对角线上的所有元素（如式（11），式（12）所示），即利用非等距线阵所能提供的全部样本信息，并且由于是一个正定Toeplitz矩阵，则波束形成在低样本采样数下仍然能得到较好的效果。

实际上，对具有连续差联合阵列的非等距线阵，若不进行Toeplitz预处理，则可利用的自由度仅为实际阵元数目；为了扩展其可用的自由度，本文基于连续差联合阵列（difference coarray）与连续波程差一一对应的原理，将原有的协方差矩阵扩展成满秩协方差矩阵，理论上扩展后的协方差矩阵等同于相同孔径等距线阵的协方差矩阵，因此，利用扩展的自由度可以抑制比阵元数多的干扰方向。本文所提方法与等距线阵中Toeplitz化的不同之处在于，等距线阵的Toeplitz化只会影响零陷深度和旁瓣高度，提高波束形成稳健性，并没有扩展自由度。下一节将对比给出具体的仿真结果。

4 波束形成仿真实验

根据以上分析，本文仿真实验采用5个阵元的最小冗余阵列作为仿真的非等距线阵，阵元位置分别位于｛0d，2d，5d，8d，9d｝，则其差联合阵列的示意图如图2所示。由图2可以看出，该最小冗余阵列的差联合阵列为与阵元位置位于的等距线阵的差联合阵列相同，故本部分仿真实验对5个阵元最小冗余阵和10个阵元等距线阵作对比来验证本文波束形成方法的正确性。

4.1 本文方法的波束形成

利用第2节的阵列模型，对上述5个阵元的最小冗余阵作波束形成，假设期望目标方向为10°， 5个非相干干扰方向分别为信噪比和干噪比均为10 dB。在快拍数为1000的情况下，根据式（14）和式（15）作波束形成如图3所示。从图3中可以看出，由于阵元间距超过半波长，带来了严重的栅瓣影响。虽然在干扰方向形成较深的零陷，但是期望目标方向受到严重干扰，这样就不利于约束期望信号方向并形成较好的波束指向。

同样采用5个阵元的最小冗余阵，干扰与期望目标方向不变，则在快拍数为1000的情况下，利用本文方法作波束形成如图4所示。从图4中可以看出，由于对最小冗余阵的协方差矩阵做了 Toeplitz预处理，波程差不会产生2π相位模糊，波束的功率在期望信号方向得到很好地聚集，其余的旁瓣也都在-10 dB以下，没有产生栅瓣现象。并且充分利用了最小冗余阵扩展的空间自由度，在干扰方向形成很深的零陷，很好地抑制了5个干扰方向。

4.2 与相同孔径等距线阵作对比

采用与 4.1节中相同的阵列模型，为了更好地验证本文所提方法可以扩展自由度，增加为9个干扰方向 -5 5°，- 40°，-25°，-10°，0°，20°，35°，50°，65°，期望方向为10°，信噪比和干噪比均为10 dB。为了更好地分析本文所提波束形成方法的效果，将最小冗余阵（MRA）与同等孔径的等距线阵（ULA）作对比，对角加载5 dB，其波束形成如图5所示。最小冗余阵采用本文提出的方法，等距线阵采用上文所述的适用于等距线阵的Toeplitz方法。从图5中可以看出，由于孔径相同，经过本文方法处理的波束形成主瓣宽度与等距线阵基本相同；同时由于在本文方法预处理中，将协方差矩阵扩展并Toeplitz化，虽然只有5个阵元但是能够很好地抑制9个干扰方向；理论上，理想情况下相同孔径的两种阵列在满足空间不模糊时，其波束方向图相同。因此，对于孔径相同的最小冗余阵与等距线阵来说，其波束方向图应该是基本一致的，但是由于两种阵列的协方差矩阵Toeplitz化后的噪声统计略有差异，导致波束方向图的旁瓣互有高低。

为了说明本文方法在低快拍下也有很好的波束形成效果，在快拍数为100的情况下，同样对角加载5 dB，对比分析最小冗余阵与等距线阵的波束形成效果如图6所示。从图6可以看出，由于两种阵列在协方差矩阵的构建中都采用了 Toeplitz的方法，虽然快拍数下降，但是仍然能够在干扰方向形成较深的零陷，实现干扰抑制。因此，本文所提方法能够利用更少的阵元数达到相同孔径 ULA所达到的性能。

图3 对最小冗余阵直接做波束形成结果

图4 应用本文方法后最小 冗余阵波束形成结果

图5 相同孔径最小冗余 阵和等距线阵对比

4.3 与文献［10］中空间平滑方法对比

根据上文分析，本部分对本文方法与文献［10］中基于KR子空间的空间平滑方法进行对比分析。期望方向，干扰方向及信号模型与4.1节仿真相同。用5个阵元的最小冗余阵作为接收阵列，在快拍数为1000的情况下，对角加载5 dB，得到两种方法的波束形成如图7所示。从图7中可以看出，本文方法和空间平滑方法都能很好地在期望方向形成波束主瓣，且主瓣宽度基本相同，但是空间平滑方法在某些干扰方向未能形成较深的零陷，干扰抑制能力会减弱。同样对比在低快拍下两种方法的效果，快拍数为100时两种方法的对比图如图8所示。从图8中可以看出，本文方法在低快拍下虽然旁瓣升高，但仍能较好地在期望方向形成波束指向，而空间平滑方法则形成了很高的栅瓣，因此，本文方法在低快拍条件下更加稳健。

4.4 同等阵元数最小冗余阵与等距线阵对比

在阵元数固定的前提下，非等距线阵扩展了孔径，获得了更多的空间自由度。采用 4.1节中的信号模型，在快拍数为1000的情况下，对角加载5 dB，对比5个阵元的最小冗余阵和5个阵元的等距线阵波束形成如图9所示。从图9中可以看出，最小冗余阵扩展了孔径，故其主瓣较窄；同时扩展了空间自由度，利用5个阵元很好地抑制7个干扰，而等距线阵则不能做到，这充分体现了非等距线阵在阵元数固定条件下的优势。

4.5 输出信干噪比

图6 低快拍下最小冗余阵和等距线阵对比

图7 本文方法与空间 平滑方法对比

图8 低快拍下本文方法与 空间平滑方法对比

图9 相同阵元数最小冗余阵与等距线阵对比

图10 输出信干噪比随输入信噪比和快拍数的变化

为了验证本文波束形成方法的有效性，采用4.1节中的信号模型，通过200次蒙特卡罗实验对比本文方法和空间平滑方法的输出信干噪比，同时用相同孔径的等距线阵和最优情况作对比，所有结果均对角加载5 dB。固定快拍数为1000，输入信噪比由-15 dB变化到30 dB，则输出信干噪比随输入信噪比的变化如图 10（a）所示。同样固定输入信噪比为10 dB，快拍数从100变化到1000，可得输出信干噪比随快拍数的变化如图10（b）所示。从图10可以看出，经过200次的蒙特卡洛实验，本文方法与最优情况更为接近，整体稳健性能要优于其他两种情况。另由图10（a）可以看出，空间平滑方法随着输入信噪比的升高，输出信干噪比下降了，这是因为产生了严重的信号相消现象，而本文方法受此影响较小。从图10（b）可以看出，在低快拍数下，如4.3节中所述，空间平滑方法在低信噪比下的效果较差，故曲线位于最下方，而本文方法则能在低快拍下较好地工作。

5 结论

本文提出了一种基于连续差联合阵列的非等距线阵接收波束形成方法，能够避免由非等距线阵阵元间距超过半波长导致的相位模糊问题，波束形成不会受到栅瓣影响，能够在期望方向形成较好的主瓣波束。本文方法与已有的基于KR子空间的空间平滑方法相比，能够在低快拍条件下得到有效的波束方向图，这对于快拍数有限情况下的稳健波束形成具有实际意义。同时在阵元数固定的情况下，由非等距线阵带来的孔径扩大，能够获得更多的空间自由度，对干扰的抑制和减小主瓣宽度有很大优势，对于天线稀疏布阵波束综合也有借鉴意义。

［1］ 徐艳红， 史小卫， 许京伟， 等. 基于响应矢量优化的共形阵列稳健波束形成［J］. 电子与信息学报， 2014， 36（9）: 2220-2226. Xu Yan-hong， Shi Xiao-wei， Xu Jing-wei， Li Ping， et al.. Robust Beamforming Based on Response Vector Optimization for Conformal Array［J］. Journal of Electronics & Information Technology， 2014， 36（9）: 2220-2226.

［2］ 杨涛， 苏涛， 何学辉. 基于波束域导向矢量估计的稳健自适应波束形成方法［J］. 电子与信息学报， 2013， 35（11）: 2758-2763. Yang Tao， Su Tao， He Xue-hui， et al.. Robust Adaptive Beamforming Based on Beamspace Steering Vector Estimation ［J］. Journal of Electronics & Information Technology， 2013， 35（11）: 2758-2763.

［3］ 杨志伟， 贺顺， 廖桂生， 等. 子空间重构的一类自适应波束形成算法［J］. 电子与信息学报， 2012， 34（5）: 1115-1119. Yang Zhi-wei， He Shun， Liao Gui-sheng， et al.. Adaptive Beam-forming Algorithm with Subspace Reconstructing［J］. Journal of Electronics & Information Technology， 2012， 34（5）: 1115-1119.

［4］ Wang X， Aboutanios E， Trinkle M， et al.. Reconfigurable adaptive array beamforming by antenna selection［J］. IEEE Transactions on Signal Processing， 2014， 62（9）: 2385-2396.

［5］ Wang X， Aboutanios E， and Amin M G. Thinned array beampattern synthesis by iterative soft-thresholding-based optimization algorithms［J］. IEEE Transactions on Antennas and Propagation， 2014， 62（12）: 6102-6113.

［6］ Friedlander B. On transmit beamforming for MIMO radar［J］. IEEE Transactions on Aerospace and Electronic Systems， 2012， 48（10）: 3376-3388.

［7］ Hua G and Abeysekera S S. MIMO radar transmit beampattern design with ripple and transition band control［J］. IEEE Transactions on Signal Processing， 2013， 61（11）: 2963-2974.

［8］ Tang Y， Ma X， Sheng W， et al.. Transmit beamforming for DOA estimation based on Cramer-Rao bound optimization in subarray MIMO radar［J］. Signal Processing， 2014， 101（2）: 42-51.

［9］ Hoctor R T and Kassam S A. The unifying role of the coarray in aperture synthesis for coherent and incoherent and imaging［J］. Proceedings of the IEEE， 1990， 12（10）: 735-752.

［10］ Pal P and Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom［J］. IEEE Transactions on Signal Processing， 2010， 58（8）: 4167-4181.

［11］ Moffet A. Minimum-redundancy linear arrays［J］. IEEE Transactions on Antennas and Propagation， 1968， 16（8）: 172-175.

［12］ Kischner A， Siart U， Guetlein J， et al.. A design-algorithm for MIMO radar antenna setups with minimum redundancy［C］. 2013 IEEE International Conference on Microwaves，Communications， Antennas and Electronics Systems（COMCAS 2013）， Tel Aviv， Israel， 2013: 1-5.

［13］ Friedlander B and Weiss A J. Detection finding using spatial smoothing with interpolated arrays［J］. IEEE Transactions on Aerospace and Electronic Systems， 1992， 28（8）: 574-587.

［14］ Ma W K， Hsieh T H， and Chi C Y. DOA estimation of quasi-stationary signals via Khatri-Rao subspace［C］. Proceedings of International Conference on Acoustics， Speech，and Signal Processing （ICASSP）， Taipei， 2009: 2165-2168.

［15］ Capon J. High-resolution frequency-wavenumber spectrum analysis［J］. Proceedings of the IEEE， 1969， 57（8）: 1408-1418.

黄 岩： 男，1991年生，博士，研究方向为阵列信号处理、动目标检测、SAR成像及运动目标参数估计.

廖桂生： 男，1963年生，教授，博士生导师，主要研究方向为阵列信号处理、动目标检测、空时自适应处理.

李 军： 男，1973年生，副教授，硕士生导师，主要研究方向为双基MIMO技术、阵列信号处理、空时自适应处理.

李 婕： 女，1992年生，博士，研究方向为阵列信号处理.

Non-ambiguity Beamforming of Nonuniform Linear Array Based on Consecutive Difference Coarray

Huang Yan Liao Gui-sheng Li Jun Li Jie
（National Laboratory of Radar Signal Processing， Xidian University， Xi’an 710071，China）

As the beamforming of Nonuniform Linear Array （NLA） may occur grating lobes phenomenon， a beamforming method is proposed for working on the NLA with consecutive difference coarray. Firstly， this method analyzes the array optimization of the NLA based on consecutive difference coarray. Additionally， it can be concluded that the consecutive difference coarray is corresponding to the consecutive wavepath difference， which is applied to reconstruct the Toeplitz covariance matrix of the NLA. According to the Least Constraint Mean Variance （LCMV） rule， the reconstructed covariance matrix can directly be used for robust adaptive beamforming. Due to the similarity between the reconstructed covariance matrix and the covariance matrix of Uniform Linear Array （ULA） with the same aperture， the phase ambiguity will not happen and the grating lobes phenomenon will not occur. Extensive simulations show the robust effectiveness of the proposed method.

Signal processing； Difference coarray； Nonuniform linear array； Non-ambiguity beamforming

TN911.7

A

1009-5896（2015）12-2891-07

10.11999/JEIT150321

2015-03-17；改回日期：2015-08-21；网络出版：2015-11-01

*通信作者：黄岩 yellowstone0636@hotmail.com