基于谱逼近的瞬态极化雷达最优波形设计

赵宜楠 姜智卓 李风从 冯 翔 周志权

（哈尔滨工业大学电子与信息工程学院 哈尔滨 150001）

基于谱逼近的瞬态极化雷达最优波形设计

赵宜楠 姜智卓 李风从 冯 翔 周志权*

（哈尔滨工业大学电子与信息工程学院 哈尔滨 150001）

针对瞬态极化雷达（IPR）两路极化波形相关度较高而导致的目标极化参数估计误差大的问题，该文提出纯相位谱逼近算法（POSAA）来设计具有低相关水平的波形对。首先，以积分旁瓣电平准则构建目标函数；然后利用相关与谱的傅里叶变换对关系，基于谱逼近的思想，推导了目标函数的频域表示；最后获得目标函数的梯度和Hess矩阵，并采用信赖域方法优化求解目标函数以获得理想波形。仿真结果表明优化后的波形对具有极低的相关水平，且利用该优化波形获得的目标参数误差远小于当前常见波形。

瞬态极化雷达；波形设计；旁瓣抑制；功率谱拟合；相位编码

1 引言

随着雷达环境的日趋复杂，设计具有低相关旁瓣的波形正受到越来越多学者的关注［1-4］。在通信和雷达领域，要求发射波形在自相关主瓣附近具有低的旁瓣，同时要求在特定区间上具有极低的互相关幅值［5］，这样不仅减少了雷达场景中距离向分布的各散射体之间的距离旁瓣干扰［6］；而且确保了在接收端，匹配滤波器可以准确地将目标距离单元的信号解调出来，同时抑制其他距离单元的反射信号［7，8］。

文献［9］提出一种循环迭代算法来设计低距离旁瓣的稀疏频谱波形，使其满足最小化功率谱密度均方差和距离旁瓣的要求，文献［10］利用模拟退火算法，面向正交组网雷达设计具有良好自相关和互相关特性的正交波形。在目前的研究中，瞬态极化雷达常采用近似全局正交波形，例如频移脉冲矢量波形［11］和正负线性调频波形［12］，但这些波形的距离旁瓣较高，会引起距离遮蔽效应，且波形正交性的限制使得极化参数估计性能不高。本文将瞬态极化雷达看作具有2个发射端和2个接收端的多输入多输出（MIMO）雷达，所以设计MIMO雷达正交波形的方法同样可用于瞬态极化雷达的波形设计。例如，当指定波形个数为 2时，文献［13］提出的 Multi-WeCAN算法即可为瞬态极化雷达的两个极化通道设计正交波形。然而，作为一种MIMO雷达波形设计算法，Multi-WeCAN必须有能力设计包含任意数量的波形集合，这使它无法针对瞬态极化雷达这样的应用作特殊的优化，因此运行效率和设计效果并不理想。

本文从另一个角度出发，根据波形的非周期相关函数与谱的傅里叶变换对的关系，面向瞬态极化雷达提出了一种纯相位谱逼近算法（Phase Only Spectral Approximation Algorithm， POSAA）来设计局部正交波形对。该方法优化两个波形，分别构造它们的自相关和互相关函数，然后使用子空间信赖域算法求解。瞬态极化雷达采用这种波形可以更好地抑制目标附近的距离旁瓣干扰，同时极化参数估计更为准确。在瞬态极化雷达的应用背景下，与Multi-WeCAN算法相比，该算法不仅具有更好的运算效率，而且设计的波形具有更低的相关水平。

2 问题建模

瞬态极化雷达系统由水平和垂直极化通道构成，发射波形的基带离散形式分别用 s1和 s2表示，系统框架如图1所示。

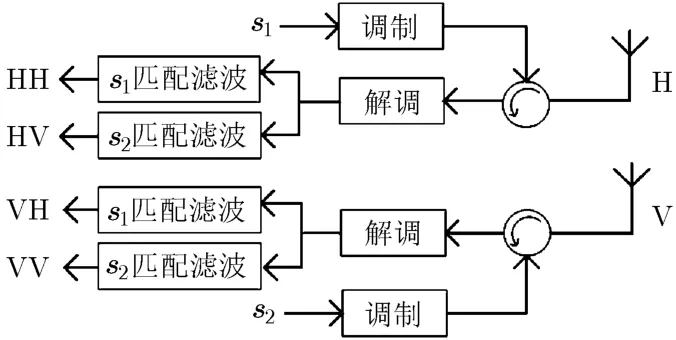
图1 瞬态极化雷达天线收发系统

当波形 s1和 s2具有较好的相关特性，即低的相关幅值时，距离旁瓣干扰和极化通道间的干扰可以大大降低。为描述对应的数学模型，引入如下的定义：

距离单元q内目标的极化散射矩阵为

序列在延迟n处的非周期相关函数表示为

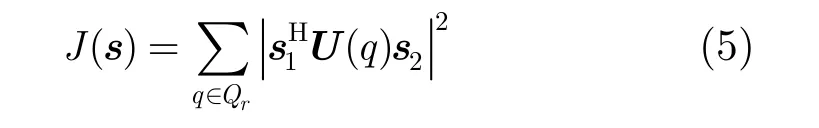
为了最大化利用发射机功率，在雷达发射机中要求发射的波形为恒模［14］，则波形优化问题表示如式（6）所示。

由目标函数式（5）的形式可以看出，为了对相关进行优化，需要计算大量数据的乘法和加法。为了提高运行效率，减少计算冗余，这里引入谱逼近算法（Spectral Approximation Algorithm， SAA）的思想，利用相关函数与谱的傅里叶变换对关系，将时域的设计目标转化为频域的设计目标。为了方便描述，首先定义如式（7）所示的蒙版向量：

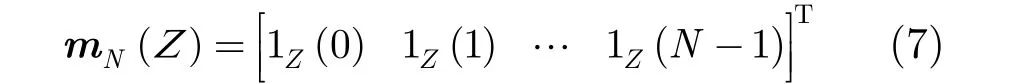
式（5）所示的目标函数可以等价为

其中N为信号波形的码长，运算符Diag将指定的向量构造为对角阵，定义如下：

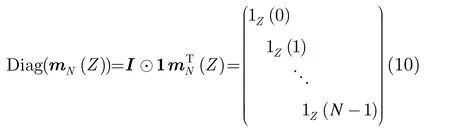
其中 rn在式（2）中定义，利用相关与谱的傅里叶变换关系，该函数可定义如式（12）：

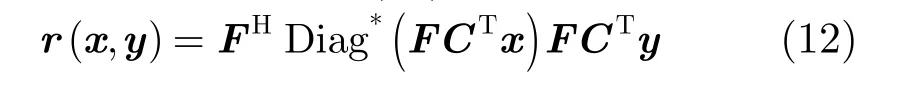
将函数 r （·，·）通过 DFT实现的定义式（12）代入目标函数得

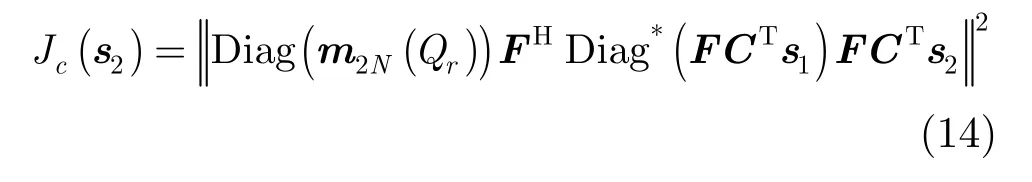
由范数的性质可知， infJc（s2）= 0，而方程 Jc（s2）= infJc（s2）在频域中的解集合可以表示为

式（15）包含的意义可以表达为：让 s2的频谱去逼近矩阵零空间中的一个向量，可以减小目标函数 Jc的值。如果不考虑任何约束条件的话，这是一个基本的子空间投影问题，可以用奇异值分解进行求解。然而，对于实际应用而言，雷达系统常常要求发射波形具有恒模特性［14］，而恒模约束使原本的线性空间投影问题变成了非凸的非线性优化问题，其数学形式如式（16）所示：

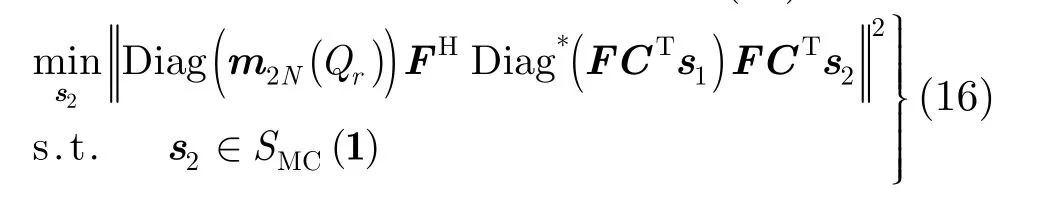
集值函数 SMC（·）定义为

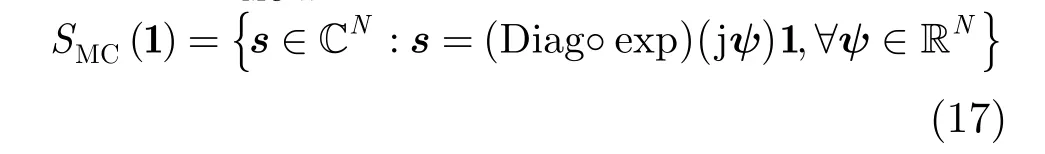
3 波形设计

由于约束条件的非线性特性，式（16）的求解非常困难。这里引入黎曼优化的概念，将波形的码元相位作为优化变量，提出名为纯相位谱逼近（POSAA）的方法。该方法利用相关和谱的傅里叶变换关系，将对波形的优化转化为对相位的优化，最后利用信赖域的思想进行求解。与 Multi-WeCAN相比，因面向对象不同进而算法的自由度提高，设计的波形在特定区间具有更低的相关水平。对于前者，其实质是2N - 1个矩阵的逼近问题，也就是 3维数组的逼近问题，不仅计算复杂度大，而且难于应用1维波形设计所适用的矩阵分析理论；而对于后者，设计的算法将3维数组的逼近问题转化为向量的逼近问题，且将时域的优化问题映射到频域利用FFT进行运算，大大提高了运算效率。

同时本文提出了串行思想设计波形，把瞬态极化雷达的波形设计分为两个步骤：第1步设计 s1满足理想的自相关要求，第2步设计 s2满足理想的自相关和互相关要求。这样可以避免由于并行处理、同时优化带来的高复杂度、高计算量的问题。

定义基带发射信号的波形矩阵为

则恒模序列 s1和 s2可以表达为［15］：

下面对算法进行推导。

3.1设计第1个波形满足自相关要求

当 s1=s2时，由式（16），式（19）得到第1个目标函数为

其中

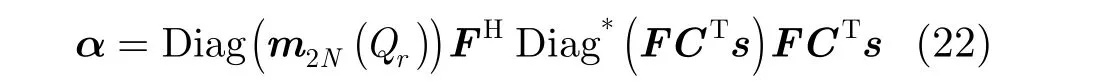
这里采用子空间信赖域的近似求解方法［16］求解这个问题，信赖域思想就是在φ的邻域，利用一阶导函数和二阶导函数即Hess矩阵，将目标函数用一个更简单的二阶函数去逼近，以此最小化目标函数。

由链式法则

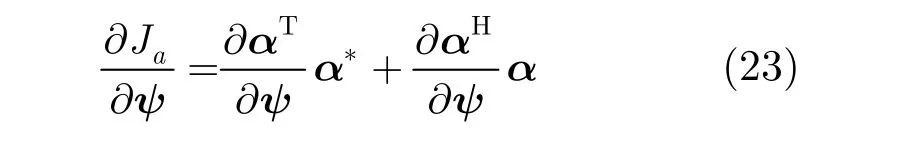
其中

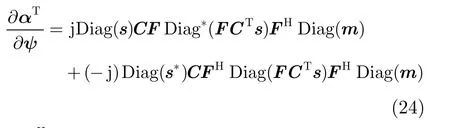
若令

则3.2 设计第 2个波形的自相关和两个波形间的互相关

当 s1确定后，由式（16），式（19）得到第2个目标函数为

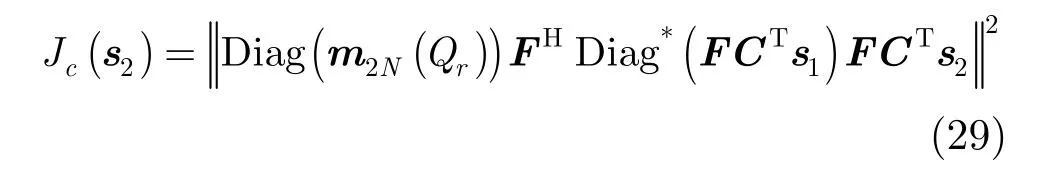
为了描述方便，记

则目标函数可化简为

可以导出：

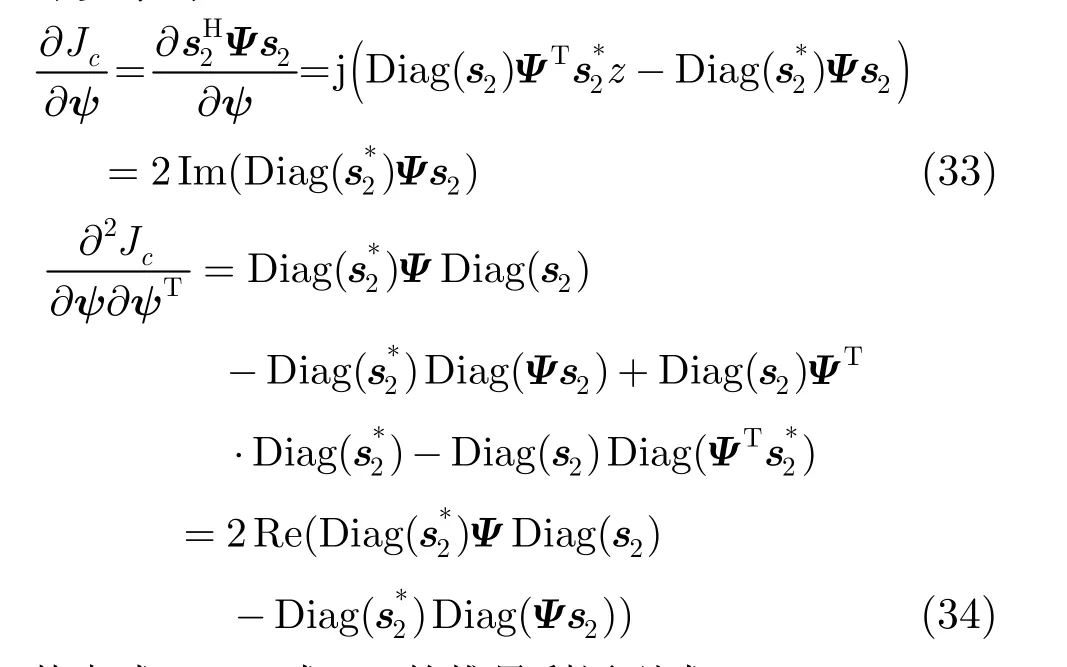
其中式（33），式（34）的推导利用到式（35）：

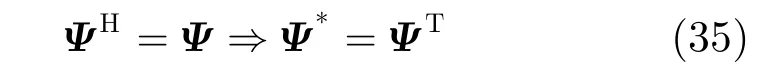
3.3 波形设计算法

由上面的分析和推导，可以得到如下的波形设计步骤：

步骤 1 设定 Qr，根据式（16）建立目标函数；

步骤 2 生成随机初始点；

步骤 3 由式（28）得到自相关目标函数的梯度矩阵，根据文献［16］提出的信赖域问题的近似解法进行求解，优化 s1满足理想自相关；

步骤 4 由式（33），式（34）分别得到互相关目标函数的梯度和Hess矩阵，优化 s2使其同时满足 s1和 s2的互相关以及 s2的自相关；

步骤 5 将求解得到的码元相位向量代入式（19），得到瞬态极化雷达两个发射通道的波形向量。3.4 极化散射矩阵的估计

瞬态极化雷达很重要的一个特点就是利用两路尽可能正交的极化信号，通过同时发射，全极化同时接收，实现在一个脉冲周期内估计出目标的极化散射矩阵的 4个元素［17］；而分时极化雷达由于交替发射两路极化信号，同时用两个极化通道对目标回波进行相参接收，所以至少需要两个脉冲周期才能完整估计出目标的极化散射矩阵；除此之外，面对运动姿态变化导致的散射特性随时间变化较快的目标，分时极化雷达很可能造成距离模糊，影响测量精度［18］。所以极化散射矩阵的估计是衡量雷达性能的关键元素。

瞬态极化雷达的回波可以表示为［19］

其中 Y =［y （1），y （2）］T∈C2×N， a为回波幅度，∑为极化散射矩阵，由式（1）定义，S为瞬态极化雷达的波形矩阵，由式（18）定义，W ∈C2×N为白噪声分量。

其中

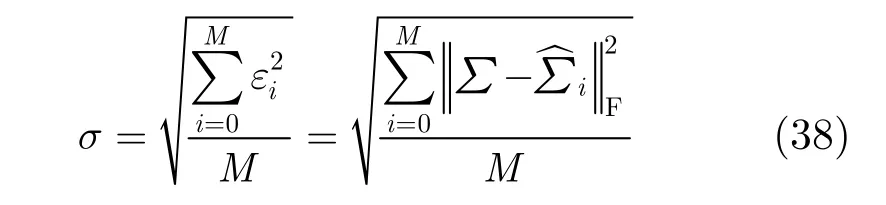
4 仿真分析与应用实例

仿真 1为了检验旁瓣抑制效果，设置以自相关序列的0延迟处为中心，1～40的相关区间为抑制区间，序列长度设置为256，设置Multi-WeCAN算法只设计两个波形。

图2（a）， 2（b）展示了本文算法POSAA设计的波形和Multi-WeCAN算法设计的波形的自相关，本文设计的两个波形在设定抑制的距离区间达到了-2 00 dB 的效果，极大的减少了雷达场景中距离向分布的各散射体之间的距离旁瓣干扰；而 Multi-WeCAN算法设计的波形自相关只达到了 -50 dB的效果。

图2（c）表示了本算法设计的波形对和 Multi-WeCAN算法设计的波形对的互相关，在抑制区间，本文设计的两个波形互相关达到 - 180 dB ，极大减少了瞬态极化雷达中不同极化通道间的相互干扰，且在接收端通过匹配滤波可以准确地得到所需要的目标信息；而Multi-WeCAN算法设计的波形对，在所要抑制的区间仅仅达到 -4 0 dB的效果。

图2 POSAA算法和Multi-WeCAN算法设计的具有单个凹口波形的各极化通道相关水平对比

表1展示了Multi-WeCAN算法和POSAA算法分别设计不同长度波形的耗时，由表中数据可以看出POSAA算法在计算量和运算效率上的优势。

表1 Multi -WeCAN与POSAA设计波形的运算时间（s）

仿真2为不失一般性，选择10～30和100～120同时作为抑制区间，其它参数设置同上，算法性能如图3所示。

可以看出，对于瞬态极化雷达，在此设置区间，本文提出的算法也要优于Multi-WeCAN算法。

仿真 3为了验证瞬态极化雷达可以利用更短的时间获得与分时极化雷达相同甚至更准确的目标信息，这里仿真了两种雷达体制利用上述设计的波形估计目标极化散射矩阵的性能，以及瞬态极化雷达分别利用本文设计的波形，Multi-WeCAN算法设计的波形和斜率相反的线性调频波形估计目标的极化散射矩阵的性能。

图4表示了利用式（38）在不同信噪比下分别做100次蒙特卡洛仿真，采用POSAA算法设计的波形，瞬态极化雷达和分时极化雷达对极化散射矩阵的均方误差对比。图中可以看出，两者对于极化散射矩阵的估计能力相当；但是由于瞬态极化雷达只用发射一个脉冲就可以获得目标的极化散射矩阵，对于散射特征随时间变化快的目标，具有良好的适应性。

图5展示了不同信噪比下分别做100次蒙特卡洛仿真，瞬态极化雷达分别采用POSAA算法设计的波形，Multi-WeCAN算法设计的波形和斜率相反的线性调频波形，由式（38），对目标极化散射矩阵的均方误差进行对比。由发射波形不同引起的极化散射矩阵的均方误差可知：POSAA算法设计的波形优于其余两种波形。

5 结束语

图3 POSAA算法和Multi-WeCAN算法设计的具有多个凹口波形的各极化通道相关水平对比

本文提出了一种波形设计算法 POSAA，该算法可以在特定区间产生具有极低相关旁瓣的波形。这类波形有效地避免了瞬态极化雷达距离旁瓣干扰和极化通道间的干扰，同时对于距离旁瓣遮蔽和多路径效应也有良好的抑制效果。POSAA基于功率谱拟合的思想，通过FFT进行运算，利用信赖域算法求解，提高了运算效率和相关水平的抑制效果。计算机仿真表明，在瞬态极化雷达的背景下，POSAA算法设计的波形相关水平能稳定保持在-1 70 dB 以下，远低于文献［13］提出的 Multi-WeCAN算法设计的波形；另外在对目标的极化散射矩阵估计和运算速度上，POSAA算法设计的波形都要优于Multi-WeCAN算法设计的波形。

图4 瞬态极化雷达和分时极化雷达在不同信噪比下对极化散射矩阵的估计误差对比

图5 瞬态极化雷达利用不同波形对 极化散射矩阵的估计误差对比

［1］ Tang B， Tang J， and Peng Y N. Waveform optimization for MIMO radar in colored noise: further results for estimation-oriented criteria［J］. IEEE Transactions on Signal Processing， 2012， 60（3）: 1517-1522.

［2］ 王旭， 纠博， 周生华， 等. 基于脉冲串编码的MIMO雷达距离旁瓣抑制方法 ［J］. 电子与信息学报， 2012， 34（12）: 2948-2953. Wang Xu， Jiu Bo， Zhou Sheng-hua， et al.. Range sidelobes suppression for MIMO radar with pulse train coding［J］. Journal of Electronics & Information Technology， 2012，34（12）: 2948-2953.

［3］ Li J， Stoica P， and Zheng X Y. Signal synthesis and receiver design for MIMO radar imaging［J］. IEEE Transactions on Signal Processing， 2008， 56（8）: 3959-3968.

［4］ 周宇， 张林让， 赵珊珊. 组网雷达低自相关旁瓣和互相关干扰的稀疏频谱波形设计方法 ［J］. 电子与信息学报， 2014， 36（6）: 1394-1399. Zhou Yu， Zhang Lin-rang， and Zhao Shan-shan. Sparse frequency waveforms design with low correlation sidelobes for Netted Radar［J］. Journal of Electronics & Information Technology， 2014， 36（6）: 1394-1399.

［5］ He H， Stoica P， and Li J. Unimodular sequence sets with good correlations for MIMO radar［C］. Proceedings of the IEEE Radar Conference， Pasadena， CA， USA， 2009: 1-6.

［6］ 李风从， 赵宜楠， 乔晓林. 抑制特定区间距离旁瓣的恒模波形设计方法［J］. 电子与信息学报， 2013， 35（3）: 532-536. Li Feng-cong， Zhao Yi-nan， and Qiao Xiao-lin. Designing phase coded waveforms with zero autocorrelation zone［J］. Journal of Electronics & Information Technology， 2013， 35（3）: 532-536.

［7］ Stoica P， He H， and Li J. New algorithms for designing unimodular sequences with good correlation properties［J］. IEEE Transactions on Signal Processing， 2009， 57（4）: 1415-1425.

［8］ Fuhrmann D R and San A G. Transmit beamforming for MIMO radar systems using signal cross-correlation［J］. IEEE Transactions on Aerospace and Electronic Systems， 2008，44（1）: 171-186.

［9］ 庄珊娜， 贺亚鹏， 朱晓华. 低距离旁瓣稀疏频谱波形相位编码设计［J］. 电子与信息学报， 2012， 34（5）: 1088-1095. Zhuang Shan-na， He Ya-peng， and Zhu Xiao-hua. Phase coding for sparse frequency waveform with low range sidelobes［J］. Journal of Electronics & Information Technology，2012， 34（5）: 1088-1095.

［10］ Deng H. Polyphase code design for Orthogonal Netted Radar systems［J］. IEEE Transactions on Signal Processing， 2004，52（11）: 3126-3135.

［11］ 戴幻尧， 刘勇， 周波， 等. 极化雷达测量体制研究进展［J］. 现代雷达， 2014， 36（1）: 1-5. Dai Huan-yao， Liu Yong， Zhou Bo， et al.. Development study of polarimetric radar system［J］. Modern Radar， 2014， 36（1）: 1-5.

［12］ 常宇亮， 王雪松， 李永祯， 等. 极化测量雷达的信号选择与处理［J］. 中国科学（F辑:信息科学）. 2009， 39（12）: 1296-1304. Chang Yu-liang， Wang Xue-song， Li Yong-zhen， et al.. Signal choice and processing of polarization radar［J］. Science in China （Series F）， 2009， 39（12）: 1296-1304.

［13］ He H， Stoica P， and Li J. Designing unimodular sequence sets with good correlations-including an application to MIMO radar［J］. IEEE Transactions on Signal Processing， 2009，57（11）: 4391-4405.

［14］ Wang Y C， Wang X， Liu H W， et al.. On the design of constant modulus probing signals for MIMO radar［J］. IEEETransactions on Signal Processing， 2012， 60（8）: 4432-4438.

［15］ Li F C， Zhao Y N， and Qiao X L. A waveform design method for suppressing range sidelobes in desired intervals［J］. Signal Processing， 2014， 96， Part B: 203-211.

［16］ Byrd R H， Schnabel R B， and Shultz G A. Approximate solution of the trust region problem by minimization over two-dimensional subspaces［J］. Mathematical Programming，1988， 40（1-3）: 247-263.

［17］ Giuli D， Fossi M， and Facheris L. Radar target scattering matrix measurement through orthogonal signals［J］. IEE Proceedings F， Radar and Signal Processing， 1993， 140（4）: 233-242.

［18］ 王雪松， 李永祯， 戴幻尧， 等. 瞬态极化雷达系统及实验研究［J］. 科学通报， 2010， 55（10）: 937-944. Wang Xue-song， Li Yong-zhen， Dai Huan-yao， et al.. Research on instantaneous polarization radar system and external experiment［J］. Chinesee Science Bulletin， 2010，55（10）: 937-944.

［19］ 赵宜楠， 庞晓宇， 王军， 等. 严重拖尾杂波中距离扩展目标的自适应极化检测［J］. 哈尔滨工业大学学报， 2014， 46（4）: 70-74. Zhao Yi-nan， Pang Xiao-yu， Wang Jun， et al.. Adaptive polarimetric detection of range spread targets in heavy-tailed compound-Gaussian clutter［J］. Journal of Harbin Institute of Technology， 2014， 46（4）: 70-74.

赵宜楠： 男，1977年生，教授，博士生导师，研究方向为雷达统计信号处理、自适应波形设计.

姜智卓： 男，1994年生，硕士生，研究方向为自适应信号处理、雷达统计信号处理.

李风从： 男，1985年生，工程师，研究方向为自适应信号处理、雷达统计信号处理、自适应极化检测器.

冯 翔： 男，1988年生，博士生，研究方向为认知雷达、雷达信号处理.

周志权： 男，1973年生，教授，博士生导师，研究方向为信号与信息处理.

Optimal Waveform Design for Instantaneous Polarization Radar via Spectral Approximation

Zhao Yi-nan Jiang Zhi-zhuo Li Feng-cong Feng Xiang Zhou Zhi-quan
（School of Electronics and Information Engineering， Harbin Institute of Technology， Harbin 150001， China）

To reduce estimation error caused by high correlation level of two transmitted waveforms， a novel method is proposed to design a couple of waveforms with low correlation level， named Phase Only Spectral Approximation Algorithm （POSAA）. Firstly， the object function is constructed under the rule of minimizing the integrated sidelobe level. Secondly， the object function is derived in frequency domain based on spectral approximation， according to the relationship between correlation sequences and the power spectral density of waveforms. Finally， the object function is optimized by trust region algorithm using its gradient and Hessian matrix. The numerical simulations have demonstrated that the designed waveforms posses a good correlation level，and the error of received target polarization information using this waveform is much less than others.

Instantaneous Polarization Radar （IPR）； Waveform design； Sidelobe suppression； Spectral approximation； Phased-coded

The National Natural Science Foundation of China （61371181）

TN958

A

1009-5896（2015）12-2964-07

10.11999/JEIT150299

2015-03-11；改回日期：2015-08-12；网络出版：2015-10-16

*通信作者：周志权 zzq@hitwh.edu.cn

国家自然科学基金（61371181）