基于同质像素预选择的极化SAR图像非局部均值滤波

杨学志陈 靖周 芳郎文辉郑 鑫李国强（合肥工业大学计算机与信息学院 合肥 230009）（光电控制技术重点实验室 洛阳 471009）

基于同质像素预选择的极化SAR图像非局部均值滤波

杨学志*①②陈 靖①周 芳①郎文辉①郑 鑫②李国强②
①（合肥工业大学计算机与信息学院 合肥 230009）②（光电控制技术重点实验室 洛阳 471009）

该文针对在极化合成孔径雷达（PolSAR）图像相干斑抑制过程中结构特征和极化散射特性保持的难题，提出一种基于同质像素预选择的非局部均值滤波算法（NLM-HPP）。该算法结合像素统计特性和极化散射机制选择滤波同质像素，并引入结构损失函数提高非局部均值（NLM）算法中像素间相似性度量的准确性，最后用改进的相似性度量对同质像素的协方差矩阵进行加权平均，实现对PolSAR图像的相干斑抑制。对真实PolSAR数据进行的实验结果表明，与现有的Refined Lee滤波、基于散射模型的滤波方法和两种非局部均值滤波相比，此方法在有效滤除相干斑点的同时能更好地保持PolSAR图像的结构信息和极化信息。

极化合成孔径雷达；非局部均值；结构保持；极化信息；同质像素预选择

1 引言

极化合成孔径雷达具有全天时，全天候的工作特征，相比于合成孔径雷达（SAR）能提供更丰富的地物目标信息。相干斑是SAR成像系统固有的原理性缺陷，它的存在影响了图像质量，并且给极化分割，极化分类，目标识别等极化数据后续处理带来困难［1］，因此相干斑抑制是PolSAR图像预处理的关键问题之一［2］。

PolSAR图像滤波方法可以归纳为两步：（1）选择一组特性相似的像素即同质像素，（2）根据同质像素估计中心像素。参与滤波的像素间特性越相似则滤波后PolSAR图像结构信息和极化信息保持效果越好，因此有效地选择同质像素参与滤波是关键问题。同质像素间的相似性主要表现在统计特性相似和极化散射特性相似两方面。像素的统计特性包括均值、方差。极化散射特性相似即具有类似的散射机制（体散射、二次散射、面散射）［3］。早期的一些滤波算法主要依据像素统计特性相似来寻找同质像素，如Refined Lee滤波［4］通过匹配边缘方向窗来确定同质像素，引入边缘结构特征，能减小边缘细节的损失，但是此方法滤波时只能使用图像局部特征，因此在结构信息保持上存在不足。

非局部均值滤波将同质像素的搜寻范围扩展到了非局部区域，具有更强的结构信息保持能力。主要滤波算法有Liu等人基于PPB算法［5］的概率形式提出的PolSAR图像的非局部均值DSM（NLDSM）滤波算法［6］和Chen等人［7］提出的Pretest（NLPretest）滤波算法。前者在最大后验概率框架下实现的相似性度量将相干斑噪声和无噪信号分开处理，不仅能抑制相干斑噪声，而且也能较好地保持图像细节。NLPretest滤波算法根据Wishart分布推导出相似性度量公式并设计了加速算法，取得了较好的降斑效果。然而这两种非局部均值滤波算法都没能有效地选择同质像素，NLDSM滤波算法在滤波前没有进行同质像素选择，NLPretest滤波算法利用了基于Wishart分布的预测验方法选择同质像素，但该方法也仅从像素统计特性角度进行选择，得到的像素不一定具有相似的散射机制。

以上滤波方法在选择同质像素时都忽略了像素的散射机制，会导致散射特性不同的像素混入同质区域，进而影响滤波后极化信息的保持。Lee等人［8］利用改进的sigma滤波器选择具有相似散射机制的邻域像素作为同质像素，较好地保持了极化散射特性。该方法与基于散射模型（Scattering-Mode-Based，SMB）的滤波方法［3］从像素极化散射特性方面选择同质像素。然而这两类方法与Refined Lee滤波方法一样，都属于局部滤波方法。

因此，本文提出一种基于同质像素预选择的非局部均值（Non Local Means based on Homogeneous Pixels Preselection， NLM-HPP）滤波算法。该方法引入边缘方向窗和sigma预选择，结合像素的统计特性和极化散射特性两个方面来选择同质像素，并且在降噪过程和结构特征间建立反馈作用机制，减少了结构信息的损失。NLM-HPP滤波算法的优势表现在以下两个方面：

（1）在极化总功率图（SPAN图）上提取边缘结构信息，根据计算的最大梯度选取方向窗，使用sigma范围在方向窗内选择具有类似散射机制的像素，从统计特性和极化散射特性两个层面提高同质像素选择的准确性，构造的滤波同质区域具有更好的散射匀质性。相比NLDSM滤波算法具有更强的结构信息和极化信息的保持能力。

（2）在 SPAN图上计算基于结构相似性指数（SSIM）［9］的结构损失函数，利用结构损失函数改进非局部均值算法中块的相似性度量，得到新的滤波权重。在降噪过程中引入了图像结构特征，能获得更好的结构信息保持效果。

本文结构安排如下：第2节介绍PolSAR图像的非局部均值滤波算法，第3节详细阐述了基于同质像素预选择的非局部均值滤波算法，第4节进行实验并分析结果，第5节是总结部分。

2 PolSAR图像非局部均值滤波算法

2005年，文献［10，11］提出了非局部均值滤波算法，该算法相比于局部滤波算法能利用更大范围的信息进行相似性估计，而且用基于块的相似性代替传统基于单个像素的相似性，取得了较好的滤波效果。因此被广泛应用于数字图像的去噪领域，随后被推广到SAR图像和PolSAR图像的相干斑抑制研究中［12，13］。非局部均值算法的滤波一般分为两步实现，（1）使用相似性度量准则给滤波像素分配对应的权重，（2）依据权重从滤波像素集合中估计中心像素的值。对于非局部均值算法在PolSAR图像的降斑应用，将NLDSM滤波算法作为特例进行阐述，滤波形式为

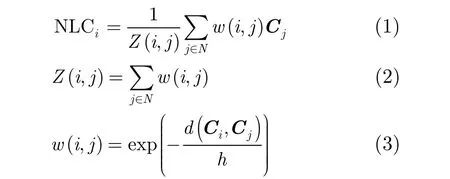
其中NLCi是像素i滤波后的协方差矩阵，Z（i，j）是归一化函数，N是以像素i为中心的搜索窗中像素的集合，Cj是搜索窗中的参与滤波的邻域像素j的协方差矩阵，w（i，j）是滤波权重，h是控制平滑程度的参数。d（Ci，Cj）是两个协方差矩阵间距离函数，描述像素间的相似性。NLPretest滤波用Wishart距离描述相似距离d（Ci，Cj），针对PolSAR图像的PPB滤波［14］用对称 Kullback Leibler（KL）距离［15］描述d（Ci，Cj），本文提出的非局部均值滤波与NLDSM滤波中d（Ci，Cj）都采用最大后验概率形式表示。

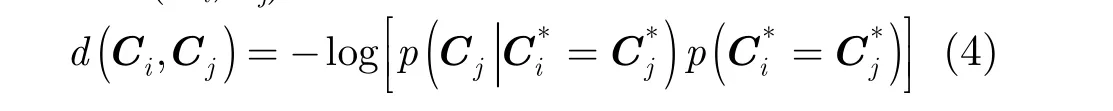
非局部均值滤波算法第2步使用的估计方法目前主要有加权平均估计（Weighted Sample Mean Estimator， WSME）、加权最大似然估计（Weighted Maximum Likelihood Estimator， WMLE）和最小均方误差（Minimum Mean Square Error， MMSE）估计［16］。NLPretest滤波和 NLDSM 滤波采用WSME，Deledalle等人提出的 PPB滤波［5］采用WMLE。NLM-HPP滤波与NLDSM滤波一致，估计方法为WSME。

NLM-HPP滤波中权重w（i，j）可以由式（3）和式（4）得到

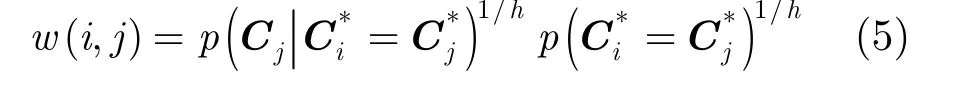
3 基于同质像素预选择的非局部均值滤波算法

PolSAR图像滤波算法在抑制相干斑的同时应当尽量避免PolSAR图像分辨率、结构信息和极化信息3方面的损失［8］。PolSAR图像中边缘、纹理等结构信息是图像解译的关键因素，直接影响PolSAR数据后续处理，选择具有相似极化散射机制的像素参与滤波能增强算法对极化信息的保持能力。从统计特性和极化散射特性两个方面选择与中心像素相似的同质像素，并且在滤波过程与结构特征之间建立反馈作用机制，能很好地提升NLDSM等非局部均值滤波对PolSAR图像结构信息和极化信息的保持能力。

图1是NLM-HPP滤波算法的过程图，从图1

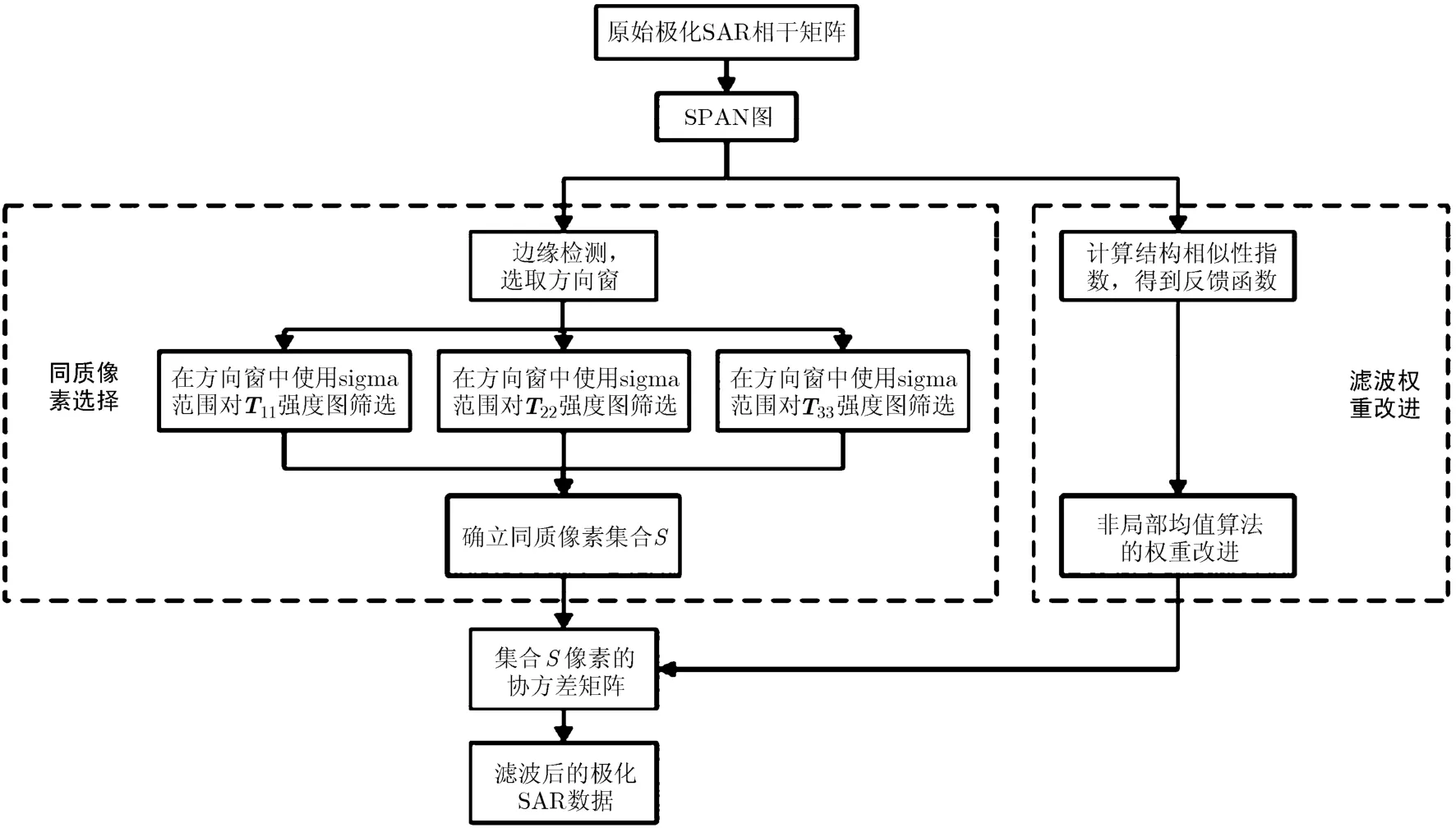
图1 NLM-HPP算法滤波过程

步骤1 在SPAN图上选取K×K的矩形窗（该窗尺寸与滤波时的搜索窗尺寸一致），将K×K的窗可以看出，本算法由两部分组成。第1部分在SPAN图上提取边缘特征，利用边缘检测结果选取方向窗，然后在方向窗中通过sigma范围选择像素构成滤波同质像素集合S。第2部分在SPAN图上计算结构相似性指数SSIM，并基于SSIM得到结构损失函数对非局部均值算法的权重进行改进。本节余下部分将详细从这两个方面阐述算法的实现过程。

3.1 同质像素的选择

NLM-HPP滤波算法将统计特性选择和散射特性选择结合，弥补了从统计特性或极化散射特性一方面选择同质区域不准确的缺陷。算法首先采用将设计好的模板与SPAN图进行匹配的边缘检测方法来选取方向窗，其次引入sigma范围作为散射一致性判断，去除方向窗中与中心像素散射机制不一致的像素，构成滤波同质区域，具体步骤如下：口划分成9个3×3的子窗（可以重叠）。计算每个子窗均值，形成一个3×3的均值窗。

步骤2 将3×3均值窗与如图2所示的4个边缘梯度模板卷积得到4个梯度值，根据最大梯度值确定边缘方向。每个边缘梯度模板对应图3（a）～3（h）中每列的2个边缘方向窗，计算3×3均值窗中中心点与边缘方向上相邻位置的像素均值差的绝对值，选择绝对值更大的方向窗作为滤波搜索窗。本文中K取5作为实例，其他尺寸的搜索窗口可以用类似方式选取。

步骤3 首先从原始PolSAR数据提取相干矩阵对角线元素T11， T22和T33的强度图，在强度图上选择矩形相似窗，并使用MMSE滤波［4］在相似窗中估计先验值T11m， T22m和T33m，其次将先验值Tkkm与sigma范围（I1， I2）相乘得到sigma强度范围（TkkmI1，TkkmI2）。文献［17］给出了不同视数下PolSAR强度图像的sigma范围（I1， I2）的计算公式。

步骤 4 通过建立的 sigma强度范围（TkkmI1，TkkmI2）对步骤2中确立的边缘方向窗内像素进行筛选，最终只有T11， T22和T33对应的3幅强度图像的强度值都符合sigma强度范围的像素才被选中，构成参与滤波的同质像素集合S。

3.2 NLM算法的权重改进

现有的NLM算法［6，7］在滤波过程中缺乏与结构特征必要的关联，无法感知滤波时结构信息的损失。因此NLM-HPP滤波算法引入SSIM建立结构损失的评价标准即结构损失函数，通过结构损失函数反馈作用于滤波权重来减少结构信息损失。首先在SPAN图上计算结构相似性指数SSIM。

ui和 σi分别为滤波搜索窗中以像素点 i为中心的相似窗Pi中像素的均值和方差，uj和 σj分别是以邻域像素j为中心的相似窗Pj中像素的均值和方差。σij表示相似窗Pi和Pj中像素的协方差，a和b是为了防止出现零除的特殊情况而设定的常数。

d（Ci，Cj）值越接近于零，表示两个像素越相似。而SSIM的取值范围为［-1，1］，当SSIM的绝对值越大时，则两个像素的相似程度越高。为了与相似性度量 d（Ci，Cj）的单调性一致，定义结构损失反馈函数R（i，j）

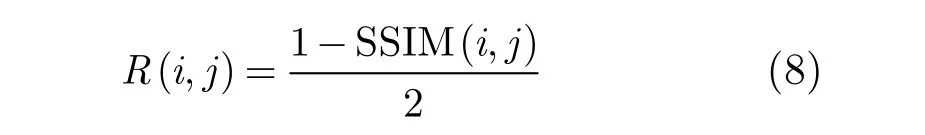
NLM-HPP滤波算法从迭代滤波的结果中得到结构损失函数R（i，j），将结构损失反馈函数R（i，j）与权重w（i，j）n相乘，修正后的权重wnew（i，j）n为

图2 4种边缘梯度模板

图3 8种边缘方向窗口

3.3 NLM-HPP滤波算法的实现过程

仅从统计特性或极化散射特性并不能有效地选择参与滤波的同质像素，为此，本文提出的NLM-HPP滤波算法将统计特性选择和散射特性选择两者结合，提高对同质区域选择的准确性，从而增强了算法对结构信息和极化信息的保持能力，并引入SSIM在每次滤波结果和相应结构特征损失间建立反馈作用机制，以迭代方式逐步去除相干斑噪声，减少了滤波过程中结构信息的损失。NLM-HPP滤波算法的滤波形式为

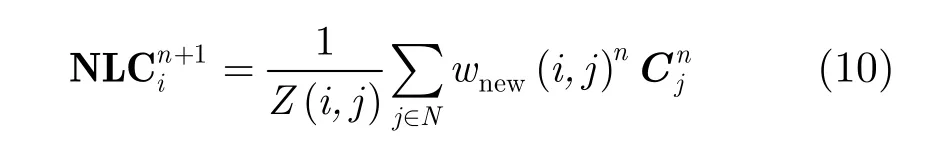
wnew（i，j）n是在滤波搜索窗N中，通过式（9）计算得到的第 n次迭代后的权重值。是像素点i第 n+1次迭代滤波后得到的协方差矩阵，Cjn是搜索窗中的参与滤波的邻域像素j第n次滤波后的协方差矩阵。通过流程图和上文分析，NLM-HPP滤波算法的实现步骤如下：

步骤1 在SPAN图上根据边缘检测结果获得边缘方向窗，用MMSE滤波估计原始极化数据的相干矩阵对角线元素的先验值Tkkm，建立sigma范围（TkkmI1，TkkmI2），在确立的方向搜索窗中选择 T11，T22和T333幅强度图像的强度值都在sigma范围中的像素构成滤波同质像素集合S。

步骤 2 在 SPAN图上计算结构相似性指数SSIM（i，j），代入式（8）得到结构损失反馈函数R（i，j）。利用反馈函数 R（i，j）对滤波权重 w（i，j）n进行改进得到修正后的权重wnew（i，j）n，使用式（10）对集合S中像素进行第1次迭代滤波。

步骤 3 根据上一次迭代滤波的结果获得新的SPAN图，由SPAN图得到新的反馈函数Rnew（i，j），使用反馈函数 Rnew（i，j）重新计算权重，之后代入式（10）对集合S中像素进行下一次迭代滤波。

4 实验结果与分析

本文对3组真实PolSAR数据进行实验。实验数据1是AIRSAR系统获取的L波段San Francisco海湾极化图像，图像视数是4视，分辨率为10 m×10 m，大小为300×300像素。实验数据2是AIRSAR系统获取的Flevoland地区的PolSAR图像，尺寸为300×300像素，以平坦区域为主。实验数据3是CONVAIR系统获取的Ottawa地区的PolSAR图像，尺寸为222×342像素。对比实验实现了Refined Lee滤波，基于散射模型（Scattering-Mode-Based，SMB）的滤波方法，NLPretest滤波和NLDSM滤波等算法。为了增加比较结果可信度，滤波参数使用相应文章中的推荐参数，Refined Lee滤波的搜索窗尺寸为7×7， SMB滤波的搜索窗尺寸为9×9，地物散射类型分为15类。NLPretest滤波、NLDSM滤波和NLM-HPP滤波均选择15×15的搜索窗和3×3的相似窗。对于NLM-HPP算法，迭代次数t的值是实验时根据滤波性能最终确定的，本文中迭代次数t为3次。

4.1 相干斑抑制效果

相干斑抑制效果可以从主观视觉判断和客观量化指标两方面评价。首先评价主观视觉效果，本文将滤波前后的PolSAR数据生成的伪彩色合成图像进行对比，其结果如图4所示。

表1 基于SPAN图的ENL值

图4（a）是原始图像，从左到右分别是 San Francisco图像，Flevoland图像和Ottawa图像。图4（b）～图4（f）是由5种滤波算法处理后的图像。图4（b）的Refined Lee滤波能去除3组实验图像中大部分噪声但是出现了边缘模糊现象和块效应。图 4（c）的SMB滤波能较好地保持图像的结构和地物散射特性，但是对相干斑的抑制能力不足，滤波后图像存在明显的残留噪声。从图 4（d）可以看出 NLPretest滤波对细节丰富的San Francisco和Ottawa图像的平滑效果很好，同时San Francisco图像中森林和城市区域的纹理结构也被平滑，然而对于平坦区域多的Flevoland图像NLPretest滤波没有有效去除相干斑。NLDSM滤波结果（图4（e））与NLPretest滤波相比，图像中细节信息丰富的区域例如原始图像标记的区域 2和区域 5的结构特征保持更好。采用NLM-HPP滤波算法处理后的图像（图4（f））滤波程度与NLPretest滤波接近，但是在结构信息保持方面比NLDSM滤波和NLPretest滤波更好，从San Francisco图像中海洋区域的强点目标保持效果和森林城市区域纹理细节保留程度可以看出。

验证算法相干斑抑制性能的客观评价标准使用等效视数（ENL）［18］。ENL能很好地度量相干斑抑制程度，ENL越大表示滤波后残留的相干斑噪声越少，得到图像越平滑。本文对3组PolSAR数据都进行了实验，得出表1原始图像和各算法去噪后图像的ENL值。 由于Flevoland图像有大块的平坦区域，因此相比实验数据1和3，实验数据2所测得ENL值能更好地验证算法的降斑能力。从表1可以看出，本文提出的NLM-HPP滤波算法能取得较大的ENL数值，这与图4所呈现的视觉效果一致。原因是该算法在选择同质像素时，除了采用边缘结构检测方法确定方向窗口外，还引入sigma范围判别像素极化散射特性是否一致，如此则使参与滤波像素与中心像素的特性更接近。因此NLM-HPP滤波算法能够在相干斑抑制和图像细节保持两者间取得较好折中，滤波结果中没有出现边缘模糊和过度平滑现象。4.2 结构信息保持效果

经过不同滤波算法滤波后，将滤波结果图与滤波前图像相比得到比值图［19］。理想比值图是只含有噪声的图像，图像中噪声分布越均匀，包含的纹理结构越少，则表明算法的结构特征保持能力越强。实验数据1的图像中边缘、纹理等细节信息丰富，并且图中有海洋、森林和城市3类区分明显的地物类型。所以本文只对实验数据1进行比值图实验，结果如图5所示。

从图 5可以明显看出 NLDSM 滤波和NLM-HPP滤波得到的比值图比其他两种算法包含更少的结构。NLM-HPP滤波与NLDSM滤波相比，比值图中噪声分布接近，反映两者的去噪能力相当，但是NLDSM滤波比值图中城市区域纹理更明显，说明去噪过程中NLDSM滤波损失的纹理更多，因此NLM-HPP滤波有更好的结构保持能力。

图4 滤波前后的伪彩色合成图

图5 不同滤波算法得到的比值图

PolSAR图像中边缘属于重要的结构信息，因此本文定量比较了滤波后图像边缘的保持效果来客观评价滤波算法对结构信息的保持能力。传统边缘保持指数（EPI）［20］能反映滤波前后图像边缘变化的程度，常用来衡量滤波算法对边缘的保持能力。SAR图像斑点属于乘性噪声，与EPI相比，EPD_ROA对受到乘性噪声干扰的边缘具有更好的鲁棒性［21］。本文选用这两种指标综合评价。EPI和EPD_ROA的值越接近1表明算法的边缘细节保持效果越好。

表2 不同区域滤波后的EPI值

表2中的区域1至区域5是分别选自图4（a）中3幅图像的结构细节丰富区域。可以看出在区域1， 2，4和5， NLM-HPP滤波取得的EPI值最大。在区域3 NLM-HPP滤波的EPI值比SMB滤波和NLPretest滤波小。表3中EPD_ROA（H）和EPD_ROA（V）是对实验数据1的标记区域1和区域2分别沿水平方向和垂直方向计算的 EPD_ROA值。结果显示NLM-HPP滤波的EPD_ROA值最高，从以上两个客观指标的结果可以看出NLM-HPP滤波对边缘结构的保持能力优于其他4类算法。原因是NLM-HPP滤波通过方向窗提取边缘结构特征，并在滤波过程中建立基于SSIM的结构损失反馈机制。因此在图像结构细节丰富区域，NLM-HPP滤波能取得更高的EPI和EPD_ROA值，在去除相干斑噪声的同时能达到较好的结构信息保持效果。

4.3 极化信息保持效果

PolSAR图像的极化信息能粗略地反映地物结构，但是结构信息的保持并不等同于极化信息保持。本文算法的改进点之一就是在确立的方向窗口中选择具有相似散射机制的同质像素参与滤波，从而提高滤波同质区的散射匀质性，尽量避免在去除斑点后破坏图像的极化信息。为了验证算法的极化信息保持能力，以极化熵值H为横轴，平均角Alpha为纵轴绘制散点在H-Alpha平面的分布图［22］。

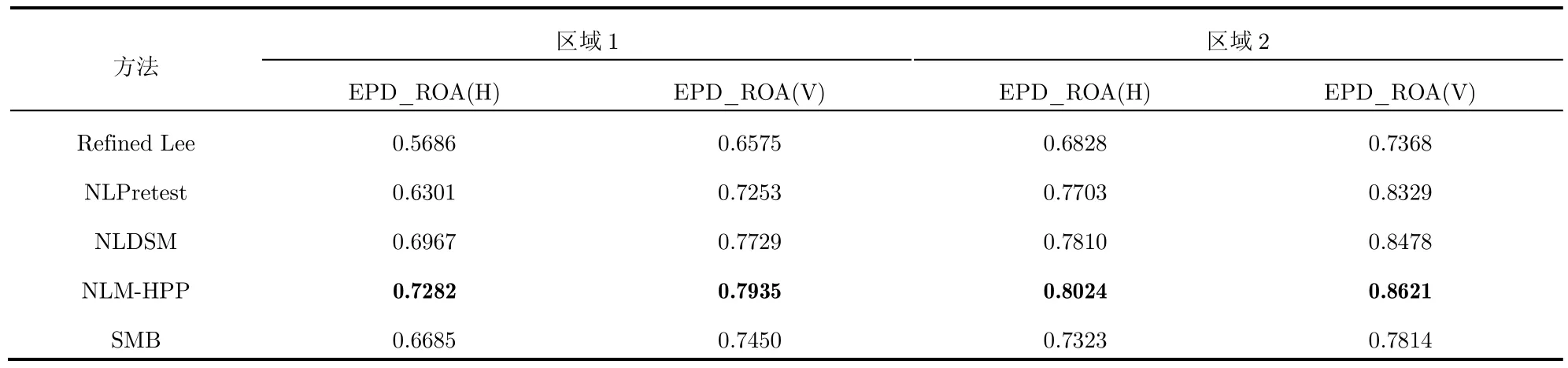
表3 不同滤波算法取得的EPD_ROA值

为观察滤波对H-Alpha参数分布影响，画出图6（a）中被标记成红色区域的H-Alpha平面图，即海洋、森林、城市区域的H-Alpha平面图。在滤波前受到相干斑噪声影响，导致原始数据图 6（b）中的 3类散射点在H-Alpha平面分布扩散。图6（c）-图6（g）是不同滤波方法处理后的H-Alpha散点分布图，滤波后3类散射点比原始数据的散射点更集中。在海洋区域，经过 NLDSM滤波、NLPretest滤波和NLM-HPP滤波处理后的散射点比Refined Lee滤波和SMB滤波处理后的散射点更加聚集，并且三者的散点聚集程度相当，表明这3种非局部均值滤波在海洋区域的平滑能力接近，并且都优于Refined Lee滤波和SMB滤波。森林区域的散射点的散射类型以高散射熵的植被散射为主，滤波后应当主要分布在散射图的高散射熵区域，NLM-HPP滤波很好地实现了这点。由于NLM-HPP算法在滤波前通过sigma范围选择具有类似散射机制的同质像素，保持了城市区域像素固有的不同散射特性，因此 NLM-HPP滤波得到的城市区域散点比其他滤波分布得更加随机。通过对极化散射特性保持效果的分析，可以看出 NLM-HPP滤波的相干斑噪声抑制能力接近NLDSM， NLPretest滤波，但是能更好地保持像素的散射机制。

通过相干斑抑制效果、结构信息保持和极化信息保持3方面分析，可以得出结论：相比Refined Lee，SMB， NLDSM和NLPretest 4种滤波算法，NLMHPP滤波算法在去除相干斑同时，具有更强的PolSAR图像结构信息和极化信息保持能力。

5 结束语

本文提出了一种改进的PolSAR图像非局部均值相干斑抑制算法（NLM-HPP）。该算法首先从像素的统计特性和极化散射特性两个方面来选择同质像素，解决了PolSAR图像滤波中同质像素的有效选择这一难题，提高了算法对图像结构信息和极化信息的保持能力，其次在相干斑降噪过程和结构特征间建立了反馈作用机制，进一步减少由于滤波导致的图像结构信息的损失。对PolSAR图像进行的实验结果表明，NLM-HPP滤波算法在有效降斑的同时能较好地保持PolSAR图像的结构信息和极化信息，有利于 PolSAR数据的后续处理。然而当PolSAR图像中相干斑噪声严重时，同质像素的选取会受到影响。因此下一步将研究如何减少相干斑噪声对同质像素选择的影响，从而提高同质像素选择的准确性。

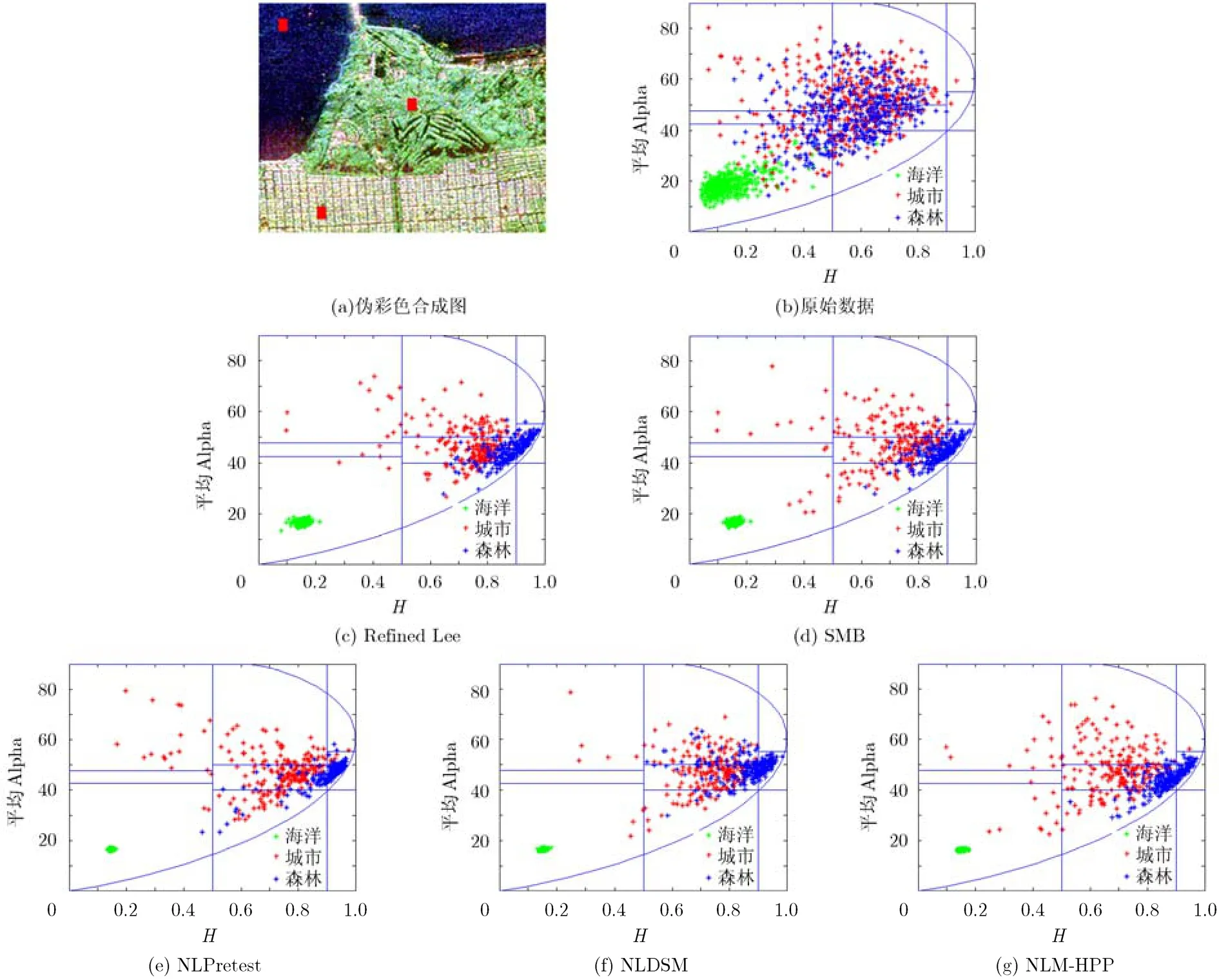
图6 海洋、森林和城市区域的H-Alpha散点分布图

［1］ Alonso-González A， López-Martínez C， and Salembier P. Filtering and segmentation of polarimetric SAR data based on binary partition trees［J］. IEEE Transactions on Geoscience and Remote Sensing， 2012， 50（2）: 593-605.

［2］ 周晓光， 匡纲要， 万建伟. 多极化 SAR图像斑点抑制综述［J］.中国图象图形学报， 2008， 13（3）: 377-385. Zhou Xiao-guang， Kuang Gang-yao， and Wan Jian-wei. A review of polarimetric SAR speckle reduction［J］. Journal of Image and Graphics， 2008， 13（3）: 377-385.

［3］ Lee J S， Grunes M R， Schuler D L， et al.. Scatteringmodel-based speckle filtering of polarimetric SAR data［J］. IEEE Transactions on Geoscience and Remote Sensing， 2006，44（1）: 176-187.

［4］ Lee J S， Grunes M R， and De Grandi G. Polarimetric SAR speckle filtering and its implication for classification［J］. IEEE Transactions on Geoscience and Remote Sensing， 1999， 37（5）: 2363-2373.

［5］ Deledalle C A， Denis L， and Tupin F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights［J］. IEEE Transactions on Image Processing， 2009，18（12）: 2661-2672.

［6］ Liu G and Zhong H. Nonlocal means filter for polarimetric SAR data despeckling based on discriminative similarity measure［J］. IEEE Geoscience and Remote Sensing Letters，2014， 11（2）: 514-518.

［7］ Chen J， Chen Y， An W， et al.. Nonlocal filtering for polarimetric SAR data: A pretest approach［J］. IEEE Transactions on Geoscience and Remote Sensing， 2011， 49（5）: 1744-1754.

［8］ Lee J S， Ainsworth T L， Wang Y， et al.. Polarimetric SAR speckle filtering and the extended sigma filter［J］. IEEE Transactions on Geoscience and Remote Sensing， 2015， 53（3）: 1150-1160.

［9］ 易子麟， 尹东， 胡安洲， 等. 基于非局部均值滤波的SAR图像去噪［J］. 电子与信息学报， 2012， 34（4）: 950-955. Yi Z L， Yin D， Hu A Z， et al.. SAR image despeckling based on non-local means filter［J］. Journal of Electronics and Information Technology， 2012， 34（4）: 950-955.

［10］ Buades A， Coll B， and Morel J M. A non-local algorithm for image denoising［C］. IEEE Computer Society Conference on Computer Vision and Pattern Recognition， San Diego， USA，2005， 2: 60-65.

［11］ 钟莹， 杨学志， 唐益明， 等. 采用结构自适应块匹配的非局部均值去噪算法［J］. 电子与信息学报， 2013， 35（12）: 2908-2915. Zhong Y， Yang X Z， Tang Y M， et al.. Non-local means denoising derived from structure-adapted block matching［J］. Journal of Electronics & Information Technology， 2013，35（12）: 2908-2915.

［12］ Torres L， Sant'Anna S J S， da Costa Freitas C， et al.. Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means［J］. Pattern Recognition， 2014，47（1）: 141-157.

［13］ Zhong H， Zhang J， and Liu G. Robust polarimetric SAR despeckling based on nonlocal means and distributed Lee filter［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（7）: 4198-4210.

［14］ Deledalle C A， Tupin F， and Denis L. Polarimetric SAR estimation based on non-local means［C］. IEEE International on Geoscience and Remote Sensing Symposium， Hawaii， USA，2010: 2515-2518.

［15］ D'Hondt O， Guillaso S， and Hellwich O. Iterative bilateral filtering of polarimetric SAR data［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2013， 6（3）: 1628-1639.

［16］ Deledalle C A， Denis L， Poggi G， et al.. Exploiting patch similarity for SAR image processing: the nonlocal paradigm［J］. IEEE Signal Processing Magazine， 2014， 31（4）: 69-78.

［17］ Lee J S， Wen J H， Ainsworth T L， et al.. Improved sigma filter for speckle filtering of SAR imagery［J］. IEEE Transactions on Geoscience and Remote Sensing， 2009， 47（1）: 691-707.

［18］ Dellepiane S G and Angiati E. Quality assessment of despeckled SAR images［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2014，7（2）: 691-70.

［19］ Hebar M， Gleich D， and Cucej Z. Autobinomial model for SAR image despeckling and information extraction［J］. IEEE Transactions on Geoscience and Remote Sensing， 2009， 47（8）: 2818-2835.

［20］ Ding Z， Zeng T， Dong F， et al.. An improved PolSAR image speckle reduction algorithm based on structural judgment and hybrid four-component polarimetric decomposition［J］. IEEE Transactions on Geoscience and Remote Sensing， 2013，51（8）: 4438-4449.

［21］ Feng H， Hou B， and Gong M. SAR image despeckling based on local homogeneous-region segmentation by using pixel-relativity measurement［J］. IEEE Transactions on Geoscience and Remote Sensing， 2011， 49（7）: 2724-2737.

［22］ Lee J S， Grunes M R， Pottier E， et al.. Unsupervised terrain classification preserving polarimetric scattering characteristics［J］. IEEE Transactions on Geoscience and Remote Sensing， 2004， 42（4）: 722-731.

杨学志： 男，1970年生，教授，博士生导师，研究方向为图像处理、模式识别及合成孔径雷达图像解译.

陈 靖： 男，1993年生，硕士生，研究方向为极化合成孔径雷达图像处理.

周 芳： 女，1987年生，讲师，研究方向为图像处理、模式识别及合成孔径雷达图像解译.

郎文辉： 男，1965年生，副教授，硕士生导师，研究方向为图像处理、模式识别及合成孔径雷达图像解译.

Polarimetric SAR Image Despeckling Using Non Local Means Filter Based on Homogeneous Pixels Preselection

Yang Xue-zhi①②Chen Jing①Zhou Fang①Lang Wen-hui①Zheng Xin②Li Guo-qiang②
①（School of Computer and Information， Hefei University of Technology， Hefei 230009， China）②（Science and Technology on Electro-optic Control Laboratory， Luoyang 471009， China）

A Non Local Means （NLM） filtering based on Homogeneous Pixels Preselection （NLM-HPP） is proposed to solve the problem of preserving structural feature and polarimetric scattering properties in speckle reduction of Polarimetric SAR （PolSAR） images. Firstly， this method combines statistical property and polarimetric scattering mechanism to select homogeneous pixels in the filtering process. Secondly， the loss function of structure is introduced to improve the accuracy of similarity measure between pixels in NLM method. Finally， it averages the covariance matrices of homogeneous pixels with the weights according to the refined similarity measure， inducing efficient reduction of the speckle in PolSAR images. The implementation results on real PolSAR images， compared with the Refined Lee filter， Scattering-Model-Based speckle filter and two kinds of Non Local Means filter，demonstrate that the proposed method can reduce speckle effectively， and further retain structural information and polarimetric information in PolSAR images.

Polarimetric SAR （PolSAR）； Non Local Means （NLM）； Structure preserving； Polarimetric information；Homogeneous pixels preselection

s: The National Natural Science Foundation of China （61371154， 41076120， 61271381， 61102154）； The Jointly funded Project for Aerospace Science Foundation and Key Laboratory of Photoelectric Control Technology （201301P4007）；The Fundameutal Research Fund for the Central Universities of China （2012HGCX0001）

TP751

A

1009-5896（2015）12-2991-09

10.11999/JEIT150314

2015-03-17；改回日期：2015-08-28；网络出版：2015-11-01

*通信作者：杨学志 hfut.cv@gmail.com

国家自然科学基金（61371154， 41076120， 61271381，61102154），光电控制技术重点实验室和航空科学基金联合资助项目（201301P4007）和中央高校基本科研业务费专项（2012HGCX0001）