雷达目标角度跟踪环路滤波器设计新方法

蒋兵兵 盛卫星张仁李 韩玉兵

（南京理工大学电子工程与光电技术学院 南京 210094）

雷达目标角度跟踪环路滤波器设计新方法

蒋兵兵 盛卫星*张仁李 韩玉兵

（南京理工大学电子工程与光电技术学院 南京 210094）

角度跟踪环路在机载雷达对目标的距离、速度、角度3维联合跟踪中起着至关重要的作用。该文分析指出传统采用卡尔曼滤波算法形成角度跟踪环路对机动目标角度进行跟踪时跟踪精度低，角跟踪误差收敛速度慢的缺点，提出弯曲度检测跟踪环路滤波器（Bend Degree Tracking Loop Filter， BDTLF）设计方法，其利用弯曲度检测角度曲线拐点，自适应地调节环路滤波器环路等效噪声带宽，并以此来控制角度跟踪环路。此算法加快了角跟踪误差的收敛速度，减轻了拐点处的角度滤波扰动，保持了滤波性能的连续性。计算机仿真结果验证了该文方法相比于卡尔曼滤波算法、粒子滤波算法、 α - β -γ滤波算法及恒定系数环路滤波器方法，对弱机动目标角度跟踪具有更加出色的性能。

角度跟踪；弱机动目标；环路滤波器；拐点检测

1 引言

机载雷达对机动目标的跟踪［1-12］，包括单目标跟踪（Single Target Tracking， STT）与多目标跟踪（Multiple Target Tracking， MTT），一直是比较重要的课题，也是当今研究目标跟踪工作进展的难点。对于线性系统，目前最常用的目标跟踪算法包括最小二乘滤波（least square filtering），卡尔曼滤波（Kalman filtering）以及交互式多模型（interacting multiple model），其中应用最多的就是卡尔曼滤波。自从1961年，Kalman提出卡尔曼滤波算法后，针对目标跟踪，学者们提出了适用于诸如白噪声加速度模型（Constant Velocity， CV）， Wiener加速度模型（Constant Acceleration， CA）、一阶时间相关模型（singer）和“当前”统计模型（Current Statistical， CS）等目标运动模型的基于卡尔曼滤波的距离、速度、角度跟踪算法。

就目标角度跟踪算法及角度跟踪环路建模而言，任波等人［1］为了提高目标跟踪的准确性和可靠性，采用纯角度跟踪模型和非线性预测滤波算法相结合的方法来确定跟踪目标的实际位置。Al-Emadi等人［2］提出了一种利用同步信号参考与振荡信号的角度跟踪技术的测量转换器，可以很简单地在基本模拟电子电路中实现，而且表现出优异的跟踪性能。赵严冰等人［3］从单脉冲雷达导引头半实物仿真出发，对包括测角单元与天线伺服单元的角度跟踪环路建模，在噪声干扰、欺骗干扰的场景下，进行了仿真实验，并重点介绍了此仿真工程实现的关键技术。孙迎丰等人［4］通过计算目标几何中心，提出了基于目标几何中心的角信息处理方法，不仅有效抑制角闪烁，而且具有更好的跟踪准确性和稳定性。朱莹等人［5］利用状态空间法仿真了噪声干扰环境下雷达角度跟踪时滞伺服系统，并对其效能进行了评估。郭宁等人［6］考虑到目标机动性特点，设计了基于“当前”机动模型的自适应椭球滤波算法，改善了光电跟踪系统的角度跟踪性能。倪震明等人［7］在对防空导弹导引头的建模仿真中，利用和差比幅测角与卡尔曼滤波（Kalman filtering）结合得到角度跟踪模型，并通过仿真验证了有效性。Hou等人［8］利用位置已知的传感器阵列，提出了一种基于扩展卡尔曼滤波以及粒子滤波的角度跟踪算法，利用每个时间步长中的单个快拍计算得到角度值。Zhang等人［9］利用融合的红外与雷达传感器测量数据，提出了用粒子滤波（particle filtering）算法对当前状态的后验均值进行估计的角度跟踪算法。Blanding等人［10］研究了对电子对抗中进入干扰区或其他遮挡区的目标进行角度跟踪的问题，他们用修正的角度测量协方差联合测量似然函数得到了更加准确的协方差矩阵测量方法，并在多个仿真算例的角度跟踪中验证了其优异的性能。Seifer［11］研究了纯噪声或噪声加干扰的环境中单脉冲雷达的角度跟踪性能。

角度跟踪环路的任务是精确地确定目标相对于所选坐标系的位置（角度）、目标的角度变化率并保持天线波束对准目标，它是决定距离、速度、角度3维联合跟踪环路性能以及能否持续跟踪目标的关键，所以提高机载雷达角度跟踪环路的性能十分有意义。

我们知道，卡尔曼滤波跟踪算法的状态方程是对目标运动状态的建模，其状态转移矩阵是决定能否精确跟踪目标的关键。一般情况下，由于无法预知目标的运动模型，采用卡尔曼滤波跟踪算法的机载数字阵列雷达在跟踪初始阶段，无法快速达到收敛状态，而且跟踪精度有限，有时甚至会出现滤波发散情况，徐景硕等人［13］提出了强跟踪滤波算法来避免这样的情况。另一方面，进入到目标跟踪末段，即机载雷达与目标接近时，从数字阵列雷达上看到的目标角度位置变化加快，基于传统卡尔曼滤波的角度跟踪算法跟踪精度大大降低，甚至无法完成对目标的跟踪。

若数字阵列雷达在搜索到目标并在转入对目标跟踪阶段时，能够快速建立角度跟踪环路，并且在当前相参处理间隔（Coherent Processing Interval，CPI）的信号处理结束后，除了完成对回波信号中角度信息的测量，又精确地预估到下个CPI所接收目标回波中携带的俯仰角、方位角信息，以此来调整天线波束指向，接收下个CPI的目标回波并进行后续的信号处理，那么从整个目标跟踪阶段来看，这样的角度跟踪环路能在很短的时间内达到收敛状态，实现对目标角度的精确跟踪。

本文采用数字阵列雷达中成熟的单脉冲测角技术［14］联合高精度测量与信号检测中常用的环路滤波器［15］设计角度跟踪环路。与采用卡尔曼滤波的角度跟踪环路相比，此方法的角度跟踪误差收敛速度更快，均方根误差也更小，但当目标弱机动，出现运动方向拐弯，即从雷达上看到目标角度曲线上出现拐点时，上述方法会在拐点发生段出现滤波扰动，破坏了滤波连续性。

由于拐点处的环路等效噪声带宽与目标稳定运动时的带宽不同，对机动目标角度跟踪的算法必须要对拐点段作调整。在弱机动目标的拐点发生段内，其角度位置的变化范围小，变化速率低，调小环路滤波器的环路等效噪声带宽，平稳地渡过拐点段，可以降低跟踪滤波性能扰动。故本文提出基于弯曲度检测的跟踪环路滤波器 （Bend Degree Tracking Loop Filter， BDTLF）设计方法，此方法在上述角度跟踪环路中增加对目标机动段角度曲线拐点的检测，一旦检测到拐点，则调小环路滤波器的环路等效噪声带宽，控制跟踪精度，若干个CPI后，对稳定运动的目标使用之前的环路等效噪声带宽，保持角度跟踪环路滤波连续性，具体框图如图1所示。

2 信号模型

数字阵列雷达的前端为相控阵，阵元数目为960，分为16个子阵，具体分布情况如图2所示。图3为机载雷达目标相对运动的示意图。

2.1 阵元级的发射信号与回波信号模型

阵元级发射脉冲多普勒信号模型如式（1）所示。

阵元级回波信号模型如式（2）所示。

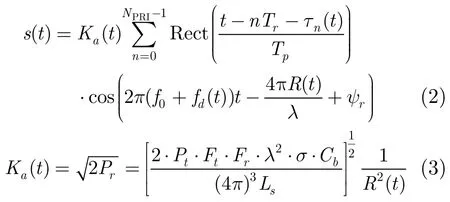
图1 基于拐点检测的角度跟踪环路

图2 子阵分布情况

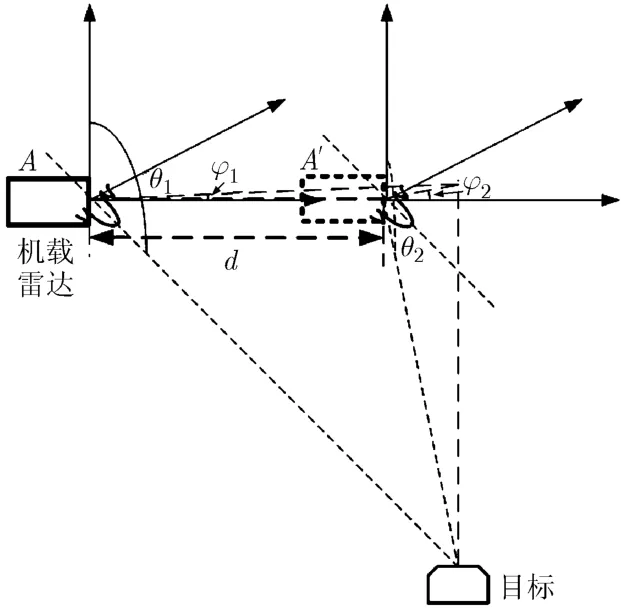
图3 机载雷达与目标运动示意图

Ft为发射方向图沿两者连线方向的增益， Fr为接收增益；σ为目标RCS值； Cb为大气衰减因子；为损失因子；λ为雷达工作波长；为脉冲发射初始时刻的斜距， v（ t）为相对径向速度）；为径向多普勒频率；为每个采样时刻对应的斜距。2.2 接收机噪声信号模型

噪声信号为带限高斯白噪声，假定其在每个阵元后端的接收机处引入，噪声带宽与接收机带宽相等。用高斯白噪声通过带限滤波器，来模拟子阵级的噪声信号。

2.3 子阵接收信号模型

子阵接收的信号由子阵内所有阵元接收信号组成，而阵元级的接收信号包含阵元回波信号与接收机噪声两个部分，设总阵元个数为N，第p个阵元的坐标为θ为俯仰角，φ为方位角，则当前波束指向下的阵列流形向量如式（4）所示。

相比于满阵条件下的接收信号模型，子阵接收信号模型中多一个子阵转换矩阵 Ts，如式（5）所示。

其中T为子阵形成矩阵，其构造方式为：设共有K个子阵，则T为一个N × K的矩阵，其每列对应一个子阵，若某个阵元在此子阵内，则对应元素置1，否则置0。故子阵接收信号为

3 基于弯曲度检测的跟踪环路滤波器设计

调节环路滤波器的等效噪声带宽可以控制环路跟踪精度及收敛快慢。在弱机动目标发生运动转向时段内的角度变化特性与目标稳定运动时的角度变化特性有区别，故其等效环路噪声带宽与目标稳定运动时是不同的。对于采用单脉冲测角技术和环路滤波器建立角度跟踪环路的机载数字阵列雷达，若其能在阵面视角方向的目标开始出现机动时检测到目标运动发生转向，并同时改变环路滤波器的等效噪声带宽，控制跟踪精度，至若干个CPI后目标运动稳定，重新使用之前的环路噪声带宽，这样就可以避免由于未对目标运动特性考虑而带来的滤波扰动，减小整个跟踪周期内角度误差的波动，得到更好的角度跟踪环路性能。对于弱机动目标的拐点发生段，可以通过调小环路滤波器的环路噪声带宽来平稳渡过。

图像处理中常采用弯曲度来判断出现拐点的像素位置［16］。通过类比的思想，本文提出了基于弯曲度检测跟踪环路滤波器设计算法（BDTLF）：计算角度变化曲线上每个点对应的弯曲度，并检测变化曲线中是否出现拐点，调整拐点处的等效环路噪声带宽，提高角度跟踪环路性能。下面是BDTLF算法的具体说明。

算法步骤：

步骤1 取点。设取点的邻域半径为r，记本次角度值为 θn（n ＞ 2r，n ∈ N+），按邻域半径往前取前两个角度值为 θn-r， θn-2r，由此得到要处理的 3个坐标，横坐标为角度值对应的CPI号，纵坐标为角度值，如式（7）所示。

步骤 3 计算这3个坐标对应的弯曲度，其值如式（9）所示［16］。

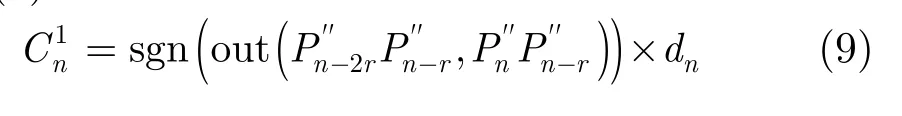
步骤 5 在后续的 NT个 CPI中使用拐点位置对应的环路等效噪声带宽进行角度跟踪；

步骤 6 NT个CPI后，使用目标稳定运动时对应的环路等效噪声带宽进行角度跟踪。

对于环路等效噪声带宽的选取，按照工程经验，应满足 BL≤ 0.1Rb，其中，BL为环路等效噪声带宽，Rb为送入环路滤波器待滤波信号的数据率。目标稳定运动时的环路等效噪声带宽按照此规则来确定，记为 BLm，取为 Rb的2% ～ 6%，拐点位置用小的环路等效噪声带宽来控制滤波精度，记为 BLc，取为BLm的0.4 ～ 0.6倍。

图4，图5所示为邻域半径 r= 2时，一些典型的曲线（加噪的半圆周、三角波和正弦波）以及真实俯仰角与方位角变化轨迹的拐点检测结果。检测结果中虽然出现了对少许非拐点位置的误判，但虚假拐点都靠近真实拐点，验证了基于弯曲度拐点检测算法的检测性能。

4 计算机仿真

图4 不同加噪曲线的拐点检测结果

图5 仿真场景中角度变化曲线的拐点检测结果

表1 仿真参数

在本文的角度跟踪环路中，系统对各路子阵回波信号进行下变频，数模转换，滤波以及抽取等处理后，得到窄带数据。再对窄带信号作数字波束形成（Digital Beam Forming， DBF）处理，形成和波束、俯仰维差波束、方位维差波束，接着用这3个波束作和差比幅单脉冲测角。得到测角误差电平后，将其按快拍依次送入环路滤波器，并将环路滤波器对最后一个快拍的输出作为本个CPI的角度跟踪环路输出值，以此来控制下个CPI天线阵面的波束指向以及DBF所需的期望信号角度，实现闭环。

文献［7］中使用的角度跟踪环路与该文类似，它利用速度波门内一段回波信号得到速度门内的和通道信号、差通道信号，之后将两者的实部取出求和，确定角误差信号，这一步骤类似和差比幅测角。在得到角误差信号后，利用基于Singer模型的机动目标卡尔曼滤波跟踪算法对角度进行跟踪。文献［9］中利用粒子滤波算法实现对机动目标的角度跟踪，此方法可以推广应用到本文的机载数字阵列雷达平台。另外，考虑到 α - β -γ滤波算法在雷达角度跟踪环路中的应用也很多，也将其推广到本文的平台中。

图6 计算机仿真场景示意图

定义第k个CPI角度滤波值与第k+1个CPI角度真实值的差值为第k个CPI的角度跟踪误差，即

图7给出了本文设计的角度跟踪环路BDTLF算法，文献［7］中采用卡尔曼滤波角度跟踪环路，文献［9］中的粒子滤波算法及常用的 α - β -γ滤波算法应用到本文雷达平台上的性能对比。

文献［7］中基于Singer模型的卡尔曼滤波算法仿真参数为：文献［9］中粒子滤波算法中使用的粒子数为量测噪声协方差矩阵状态噪声协方差矩阵-γ滤波算法中从图 7可以看出，在角度跟踪初始阶段，5种方法都有较好的跟踪精度。随着跟踪状态的进行，其它3种方法由于其状态转移矩阵与目标真实运动轨迹模型之间的偏差变大，滤波效果也随之变差；然而，采用恒定LF（Loop Filter）系数的角度跟踪环路在角度跟踪过程中，跟踪误差稳步减小，并逐渐达到收敛的状态，虽然在部分位置出现滤波偏差突变的情况，但仍能够收敛。另一方面， BDTLF能更快地进入收敛状态，而且精度也相对较高。在方位角跟踪曲线中，第142个CPI出现拐点，恒定LF系数作用下的角度跟踪环路的滤波性能出现扰动，而 BDTLF则表现出较好的跟踪连续性以及稳定性。

表2为5中方法分别在俯仰维、方位维的角度跟踪均方根误差对比情况。对于弱机动目标的角度跟踪，使用环路滤波的跟踪环路的跟踪性能要优于采用卡尔曼滤波的角度跟踪环路，其不仅能够保证滤波误差的收敛，而且跟踪均方根误差也更小。恒定 LF系数角度跟踪环路的跟踪均方根误差为卡尔曼滤波的13%左右，角度跟踪性能显著提高。本文提出的基于弯曲度检测的跟踪环路设计算法BDTLF相比于恒定LF系数作用下的角度跟踪环路性能更好。其次，运用BDTLF算法，使得跟踪误差收敛更快，并且跟踪均方根误差减小为使用恒定LF系数的40%左右，为卡尔曼滤波算法的5%左右，较好地提升了跟踪环路的性能。

表2 5种方法在两个维度角度跟踪均方根误差比较（rad）

图8给出BDTLF算法的拐点检测性能。可以看出，BDTLF算法能够检测出真实的拐点，但也会发生误判，但错误概率在能接受的范围内。另一方面，在BDTLF发生检测错误时，得到虚假拐点的位置靠近真实拐点，对角度跟踪性能的破坏较小，可以论证BDTLF具有较好的拐点检测性能，而且从其得到的角度跟踪误差性能上能够看出：BDTLF适用于机载雷达对弱机动目标的角度跟踪。

最后，再讨论关于BDTLF中拐点位置对应的等效环路噪声带宽使用CPI数的确定问题。图9为BDTLF中在不同的邻域半径以及不同的拐点位置对应的等效环路噪声带宽作用CPI数条件下得到的角度跟踪环路的滤波标准差，颜色深的方块对应的标准差小。可以看出，当邻域半径为 r= 2，拐点位置对应的环路滤波系数作用的CPI数为3～6时，俯仰角与方位角的角度跟踪均方根误差都比较小，本

作为典型值仿真。

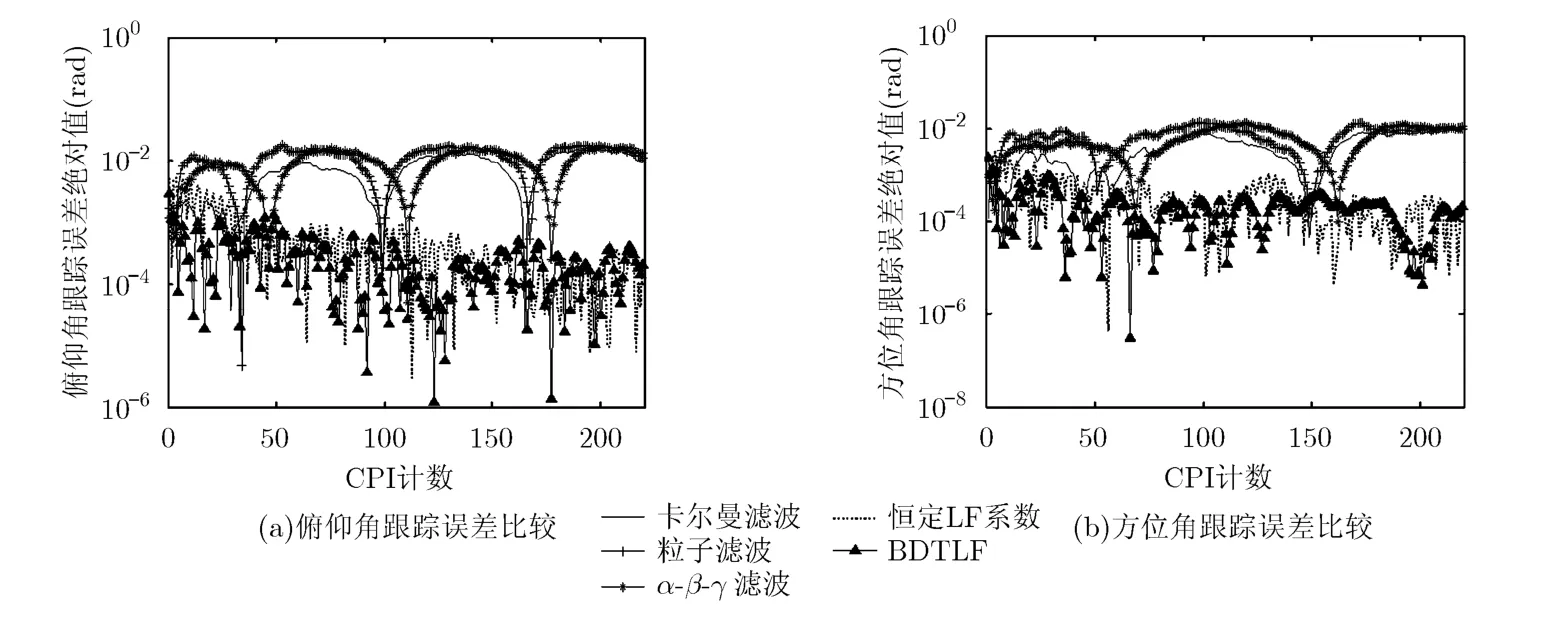
图7 角度跟踪环路性能比较

图8 BDTLF对俯仰角、方位角的拐点实测结果

图9 BDTLF对俯仰角、方位角的滤波标准差

5 结束语

本文提出了一种新的机载数字阵列雷达对弱机动目标的角度跟踪算法：基于弯曲度检测的跟踪环路滤波器（BDTLF）设计，可以对目标角度变化曲线上的拐点进行检测，自适应地调节环路滤波器的环路噪声带宽，加快了角度跟踪环路的收敛速度，并且抑制了目标角度在拐点处发生滤波扰动，保持了滤波性能的连续性与稳定性。计算机仿真结果验证了BDTLF算法对雷达目标角度变化曲线拐点检测性能。通过与其它算法对比，在机载数字阵列雷达平台上对弱机动目标角度跟踪时，BDTLF算法得到的角误差收敛性能更加出色。

［1］ 任波， 闫向远. 纯角度跟踪非线性预测滤波算法研究［J］. 弹箭

与制导学报， 2014， 34（2）: 6-8.Ren Bo and Yan Xiang-yuan. Bearing-only tracking nonlinearprediction filter algorithm research［J］. Journal of Projectiles，Rockets， Missiles and Guidance， 2014， 34（2）: 6-8.

［2］ Al-Emadi N， Ben-Brahim L， and Benammar M. A new tracking technique for mechanical angle measurement［J］. Measurement， 2014， 54（8）: 58-64.

［3］ 赵严冰， 陈正宁. 单脉冲雷达导引头角度跟踪环路半实物仿真［J］. 现代防御技术， 2014， 42（6）: 146-152. Zhao Yan-bing and Chen Zheng-ning. Hardware-in-loop simulation of angle tracking loop for monopulse radar seeker［J］. Modern Defense Technology， 2014， 42（6）: 146-152.

［4］ 孙迎丰， 刘旭东， 张磊， 等. 基于目标几何中心的高分辨雷达角跟踪方法［J］. 中国电子科学研究院学报， 2014， 18（2）: 194-198. Sun Ying-feng， Liu Xu-dong， Zhang Lei， et al.. Angular tracking method based on the geometric center of target in high resolution radar［J］. Journal of CAEIT， 2014， 18（2）: 194-198.

［5］ 朱莹， 王金广， 高其娜， 等. 噪声干扰下雷达角度跟踪时滞伺服系统仿真［J］. 系统仿真学报， 2014， 26（8）: 1814-1819. Zhu Ying， Wang Jin-guang， Gao Qi-na， et al.. Noise jam on angle tracking radar delay servo system simulation［J］.Journal of System Simulation， 2014， 26（8）: 1814-1819.

［6］ 郭宁， 吕俊伟， 邓江生. 光电跟踪系统纯角度滤波器的设计［J］.光学精密工程， 2013， 21（7）: 1818-1824. Guo Ning， Lü Jun-wei， and Deng Jiang-sheng. Design of filter only by angle information in opto-electronic tracking system［J］. Optics and Precision Engineering， 2013， 21（7）: 1818-1824.

［7］ 倪震明， 陈长海， 刘俊. 防空导弹导引头建模与仿真［J］. 现代电子技术， 2012， 35（17）: 25-29. Ni Zhen-ming， Chen Chang-hai， and Liu Jun. Modeling and simulation of air-defense missile seeker［J］. Modern Electronics Technique， 2012， 35（17）: 25-29.

［8］ Hou S Y， Hung H S， and Kao T S. Extended Kalman particle filter angle tracking （EKPF-AT） algorithm for tracking multiple targets［C］. 2010 IEEE International Conference on System Science and Engineering （ICSSE）， Taipei， 2010: 216-220.

［9］ Zhang G， Liang J， Zhao H， et al.. Sequential Monte Carlo implementation for infrared/radar maneuvering target tracking［C］. The WCICA 2006 IEEE Sixth World Congress on Intelligent Control and Automation， Dalian， 2006: 5066-5069.

［10］ Blanding W R， Koch W， and Nickel U. Adaptive phasedarray tracking in ECM using negative information［J］. IEEE Transactions on Aerospace and Electronic Systems， 2009，45（1）: 152-166.

［11］ Seifer A D. Monopulse-radar angle tracking in noise or noise jamming［J］. IEEE Transactions on Aerospace and Electronic Systems， 1992， 28（3）: 622-638.

［12］ Sword C K， Simaan M， and Kamen E W. Multiple target angle tracking using sensor array outputs［J］. IEEE Transactions on Aerospace and Electronic Systems， 1990，26（2）: 367-373.

［13］ 徐景硕， 秦永元， 顾冬晴. 控制 Kalman 滤波器发散的方法研究［J］. 弹箭与制导学报， 2004， 24（1）: 249-252. Xu Jing-shuo， Qin Yong-yuan， and Gu Dong-qing. Research on schemes for restraining Kalman filter divergence［J］. Journal of Projectiles， Rockets， Missiles and Guidance， 2004，24（1）: 249-252.

［14］ 刘宏伟， 张守宏. 平面阵线性约束自适应单脉冲测角算法［J］.电子与信息学报， 2001， 23（3）: 275-279. Liu Hong-wei and Zhang Shou-hong. Linearly constrained adaptive monopulse estimation algorithm for planar array［J］. Journal of Electronics & Information Technology， 2001， 23（3）: 275-279.

［15］ Chung B， Chien C， Samueli H， et al.. Performance analysis of an all-digital BPSK direct-sequence spread-spectrum IF receiver architecture［J］. IEEE Journal on Selected Areas in Communications， 1993， 11（7）: 1096-1107.

［16］ 廖文志， 皮佑国. 基于双重弯曲度积的图像拐点检测术［J］. 华南理工大学学报（自然科学版）， 2010， 38（2）: 132-136. Liao Wen-zhi and Pi You-guo. Corner detection of image based on product of two bending degrees［J］. Journal of South China University of Technology （Natural Science Edition），2010， 38（2）: 132-136.

蒋兵兵： 男，1990年生，博士生，研究方向为雷达信号处理，目标跟踪技术.

盛卫星： 男，1966年生，教授，博士生导师，主要研究方向为数字波束形成、智能天线、电磁散射模型以及图像处理.

张仁李： 男，1986年生，讲师，硕士生导师，主要研究方向为雷达信号处理、恒虚警检测、杂波检测与杂波抑制.

韩玉兵： 男，1971年生，副教授，博士生导师，主要研究方向为阵列信号处理、视频图像处理.

A Novel Design Method of Radar Target Angle Tracking Loop Filter

Jiang Bing-bing Sheng Wei-xing Zhang Ren-li Han Yu-bing
（School of Electronic and Optical Engineering， Nanjing University of Science and Technology， Nanjing 210094， China）

The angle tracking loop in airborne radar facing to a maneuvering target plays a vital role in the joint 3D-tracking of range， velocity and angle. This paper analyses the disadvantage of the conventional Kalman filter algorithm employed to track a maneuvering target’s angle， which are a low tracking precision and a slow convergence rate of angle tracking error. In order to solve these problems， a novel angle tracking algorithm called Bend Degree Tracking Loop Filter （BDTLF） is put forward to detect the corners in target’s angle curve by bend degree detection and adjust the loop noise bandwidth adaptively to control angle tracking loop. The proposed algorithm accelerates the convergence rate in angle tracking loop， lightens the filtering disturbance around target’s angle curve corners， and keeps the continuity of filtering performance. The computer simulation results demonstrate that compared with the angle tracking loop using Kalman filtering algorithm， particle filtering algorithm， α - β -γ filtering algorithm or a constant coefficient loop filter， this novel method has a more satisfying performance in angle tracking of weakly maneuvering targets.

Angle tracking； Weakly maneuvering target； Loop filter； Corner detection

The National Natural Science Foundation of China （61401207）

TN953.5

A

1009-5896（2015）12-2948-08

10.11999/JEIT150389

2015-04-02；改回日期：2015-07-08；网络出版：2015-08-27

*通信作者：盛卫星 shengwx@njust.edu.cn

国家自然科学基金（61401207）