基于空谱联合的多假设预测高光谱图像压缩感知重构算法

王 丽 冯 燕

（西北工业大学电子信息学院 西安 710129）

基于空谱联合的多假设预测高光谱图像压缩感知重构算法

王 丽 冯 燕*

（西北工业大学电子信息学院 西安 710129）

为充分利用高光谱图像的空间相关性和谱间相关性，该文提出一种基于空谱联合的多假设预测压缩感知重构算法。将高光谱图像分组为参考波段图像和非参考波段图像，参考波段图像利用光滑Landweber投影算法重构，对于非参考波段图像，引入空谱联合的多假设预测模型，提高重构精度。非参考波段图像中每个图像块的预测值不仅来自非参考波段图像未经预测的初始重构值的相邻图像块，而且来自参考波段重构图像相应位置及其邻近的图像块，利用预测值得到测量域中的残差，然后对残差进行重构并对预测值进行修正，此残差比原图像更稀疏，且算法采用迭代方式提高重构图像的精度。借助Tikhonov正则化方法求解多假设预测的权重系数，并基于结构相似性判断是否改变多假设预测搜索窗口大小，最后利用交叉验证计算重构算法终止迭代的判据参数。实验结果表明，所提算法优于仅利用空间相关性或谱间相关性进行预测和不预测的重构算法，其重构图像的峰值信噪比提高2 dB以上。

高光谱图像；压缩感知；空谱联合的多假设预测；Tikhonov正则化；结构相似性

1 引言

高光谱图像既含有地物的空间分布信息，又能对每个像元提取一条连续光谱曲线，故其在特征分类［1］、目标探测［2］、农业监测［3，4］等方面应用广泛。但高光谱图像数据量大，给传输和存储都带来较大的困难，一般采用预测、变换、矢量量化等压缩技术达到减少数据量的目的。随着人们对信息需求量的急剧增加，寻找有效的数据压缩和重构算法对高光谱遥感技术的发展十分重要。

压缩感知理论（Compressed Sensing， CS）［5，6］指出：对于稀疏或可压缩信号，可通过远低于奈奎斯特速率进行采样，仍能精确恢复出原始信号。该理论将采样与压缩过程结合，直接采集数据的信息特性，已成功应用于医学成像［7］、传感器网络［8］、视频图像［9］以及波达方向估计［10，11］等领域。高光谱图像同时存在空间冗余和谱间冗余，其图像具备可压缩性［12］，利用 CS理论进行采样后，需从少量的观测值通过求解优化问题恢复出原始图像，因此重构算法对实现高光谱压缩感知有重要影响。

高光谱图像的每个波段图像可采用已有的2维压缩感知重构算法进行重构，如以基追踪算法［13］、梯度投影稀疏重构算法［14］为代表的凸优化算法，以贝叶斯算法为代表的统计优化算法［15］和以匹配追踪算法为代表的贪婪算法［16］，或重构每个像元向量的主成分分析算法［17］等。为降低采样复杂度，分块压缩感知（Block Compressed Sensing， BCS）［18］在采样端将图像分块测量，并利用光滑 Landweber投影（Smoothed Projected Landweber， SPL）算法高效高精度地恢复原始图像。为利用高光谱图像的谱间相关性，出现了基于谱间相关性提高重构精度的算法，如文献［19］提出的多目标贝叶斯压缩感知方法，以及针对CASSI成像光谱仪的重构算法［20，21］。更多利用谱间相关性的算法则是基于谱间预测，如文献［22］提出的基于谱间预测和联合优化的高光谱压缩感知重构算法及基于谱间最佳线性预测的改进算法［23］。得到波段图像预测值的方法包括针对视频图像的运动估计和运动补偿［24］及自回归模型［25］，针对高光谱图像的双向预测［26］等。文献［27］还提出了针对视频图像和静止图像的多假设预测方法，文献［28］将其应用于高光谱图像，但仅利用了高光谱图像光谱向量的空间相关性。

本文提出一种基于空谱联合的多假设预测高光谱图像压缩感知重构算法，在采样端，将高光谱图像进行分组处理，每组图像包括参考波段图像和非参考波段图像，对各个波段图像采用分块压缩感知采样来获取测量值。在重构端，采用SPL算法得到参考波段图像的重构值和非参考波段图像的初始重构值。为充分利用波段图像相邻块的空间相关性及相邻波段图像的谱间相关性，以恢复的参考波段图像和非参考波段图像为基础，采用空谱联合的多假设预测模型得到非参考波段图像的预测值，计算预测残差及其对应的测量值，通过重构残差来修正预测值，以此得到非参考波段图像的重构值，算法采用迭代方式提高重构精度。实验结果表明，所提算法优于仅利用空间相关性或谱间相关性进行预测的重构算法和不预测的重构算法。

2 高光谱图像分块压缩感知测量及重构

2.1 压缩感知理论

压缩感知理论的本质是将采样与压缩相结合，利用信号稀疏表示的先验知识，采用少量非自适应线性测量的方式即可获取原信号足够的信息，如N维信号可以通过少量的M(M ≪ N)个测量值以高概率进行恢复。在该理论框架下，采样速率不取决于信号的带宽，而取决于信号中信息的结构和内容。对于一个实值的长度为N的1维离散信号x，可用一组正交基向量对其进行稀疏分解，即经过某组正交基或紧框架Ψ的变换后，其变换系数是稀疏的：

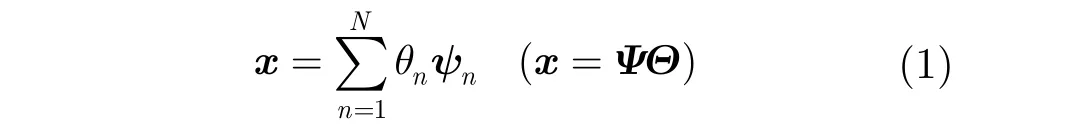
若变换系数 θn支撑域的势小于等于K，则称信号为K-项稀疏信号。若系数遵循指数规律，除了少数几个大系数幅值较大外，其余系数迅速衰减至0，则称信号为可压缩信号。

对稀疏信号x进行线性测量，测量值为

数据重构时，需从M个测量值恢复长度为N的原始信号，由于M ≪ N，直接由y求解x相当于求解欠定方程组，但在信号稀疏或可压缩的前提下，上述问题可转化为求解最小l0范数问题：

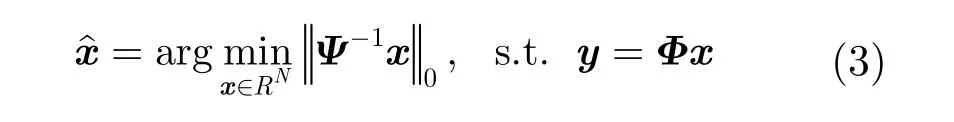
然而l0优化是一个 NP难问题，求解该问题的典型算法是基追踪算法，将 l0优化转化为l1优化问题，即

2.2 分块压缩感知测量及重构

对于高光谱图像来说，因图像尺寸很大，存储测量矩阵会增加内存负担，且重构非常耗时。为降低计算复杂度，采用分块压缩感知测量以减少测量矩阵的内存。在分块压缩感知中，将大小为 N1×N2的波段图像分成互不重叠的大小为B × B的块，每个图像块的测量矩阵为 φB，对于第 l个图像块 xl，，其测量值为

对于整幅图像来说，其测量矩阵为块对角矩阵：

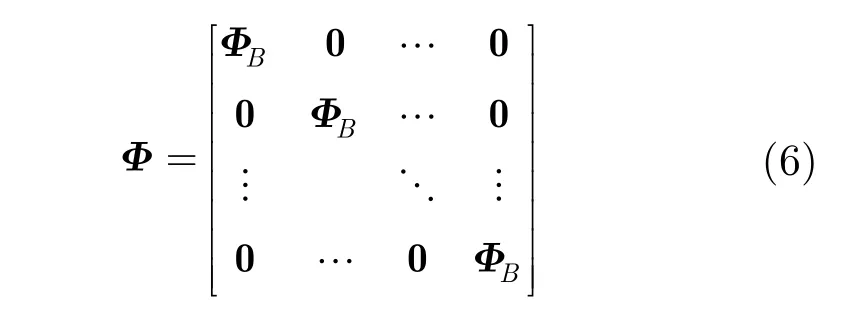
虽然利用追踪类算法能有效处理线性投影的重构问题，但计算复杂度较高，因此出现了基于投影的技术，称为PL（Projected Landweber）方法［29］。此类方法主要通过交替投影和阈值去噪来实现信号的逼近，其迭代过程从某个初始近似值开始，第 m+1次迭代过程为

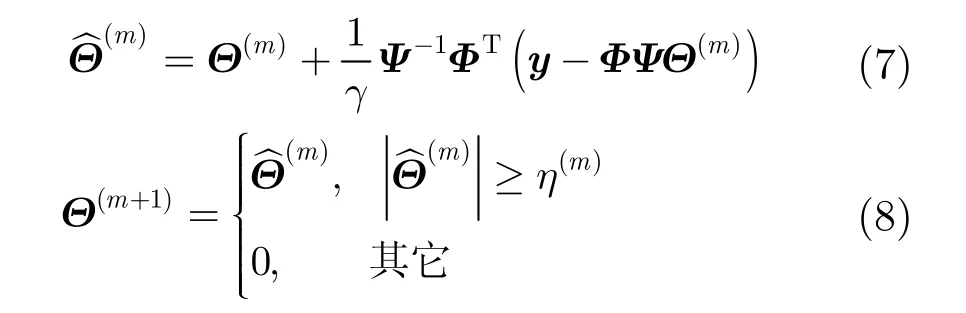
其中，Ψ为稀疏分解矩阵，φ为测量矩阵，y是图像x的随机测量值，Θ为图像x的稀疏表示形式，γ为尺度因子，取值为 φTφ的最大特征值， η（m）是每次迭代设置的阈值，m为迭代次数。该方法不仅能降低算法复杂度，且能增加其他优化准则，有利于进行相关处理。当利用 PL方法对每个图像块单独重构时，由于没有考虑图像块之间的相关性，重构结果出现块效应，可利用维纳滤波器来平滑块效应［30］。

3 基于空谱联合的多假设预测重构算法

高光谱图像的每个波段图像可采用 BCS_SPL算法进行采样和重构，但高光谱图像同时具有空间和谱间相关性，可利用空间和谱间相关性提高重构精度，为此本文提出基于空谱联合的多假设预测重构算法（Spatial-Spectral MultiHypothesis Prediction BCS_SPL， SS_MH_BCS_SPL）。图1为SS_MH_ BCS_SPL算法框图，在采样端，将高光谱图像进行均匀波段分组，分组大小为Q，分组序号为k，每个波段图像组包括一个参考波段图像 xk，ref和多个非参考波段图像 xk，j（j = 2，3，…， Q ），此处的 xk，j是对应波段图像的向量化表示，图中仅给出一个分组的示意，其他分组与之相同。为降低采样端的计算复杂度，对每个波段图像进行独立分块压缩感知采样，不进行预测集合选择及处理。在重构端，首先采用 SPL算法得到参考波段图像重构值 xˆk，ref和非参考波段图像的初始重构值 xˆk0，j。其次，利用SS_MH_BCS_SPL算法重构非参考波段图像，算法以迭代方式进行。在第i次迭代时，利用参考波段图像的重构值 xˆk，ref和非参考波段图像的重构值xˆik-，j1，借助空谱联合的多假设预测模型获取非参考波段图像的预测值j，并采用相同的测量矩阵得到预测值的测量值，在此基础上获取预测测量值和原始测量值之间的差值，利用SPL算法对残差进行重构，最后利用残差重构值对预测值进行修正，得到非参考波段图像的重构值j（j = 2，3，…， Q ）。满足迭代终止条件后，算法结束。

3.1 多假设预测

为提高非参考波段图像的重构精度，利用参考波段图像对非参考波段图像进行预测，然后进行预测残差重构。算法的基本思想是：如果预测值与原图像很接近，则预测残差将比原图像更稀疏，可利用重构残差去修正预测值。其关键是找到原图像的预测值，然后对预测值和原图像之间的残差进行测量和重构，得到残差重构值后，对预测值进行修正，并通过迭代方式提高重构精度。该算法可行的原因在于：假设x~是x的预测值，则满足 x~ ≈x，预测残差为利用测量矩阵φ得到残差的测量值为则原图像的重构为：其中，Rc（·）表示某种CS重构算法。

若预测过程足够精确，则残差Δx应比原图像x更稀疏，因此由Δy进行重构得到Δx，应比直接从原始测量值y恢复x更有效。为得到稀疏度更高的残差，需要获取与原图像x较为接近的预测值，即优化式（9）所示问题：

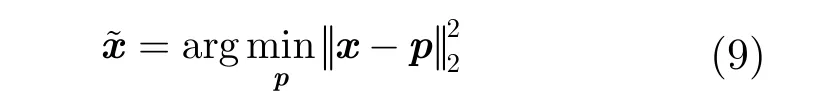
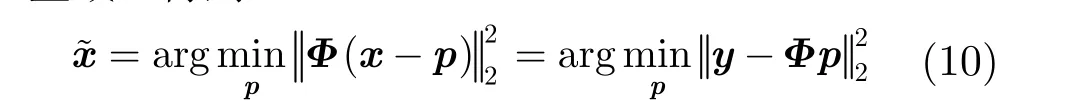
Johnson-Lindenstrauss （JL）引理［31］表明：利用服从一定分布的随机投影可将N维欧式空间中任意包含N个点的集合映射到M维的欧式子空间，若满足且0 ＜ ε＜ 1，则该映射能以很高的概率保持原空间中任何两点的距离变化任意小。因此，式（10）与式（9）的解应是一致的。

对于高光谱图像，每个图像块进行预测的目标是寻找式（10）的最优解，将预测值表示为候选集中所有预测的线性组合，即其中，下标k表示组号，j表示波段图像号，l表示图像块号， xk，j，l表示当前图像块， Hk，j，l表示由所有候选集中的预测图像块组成的矩阵，其每一列为不同候选预测图像块的向量化表示，则将图像块 xk，j，l的多假设预测过程转化为求解线性组合中系数权重的问题，即

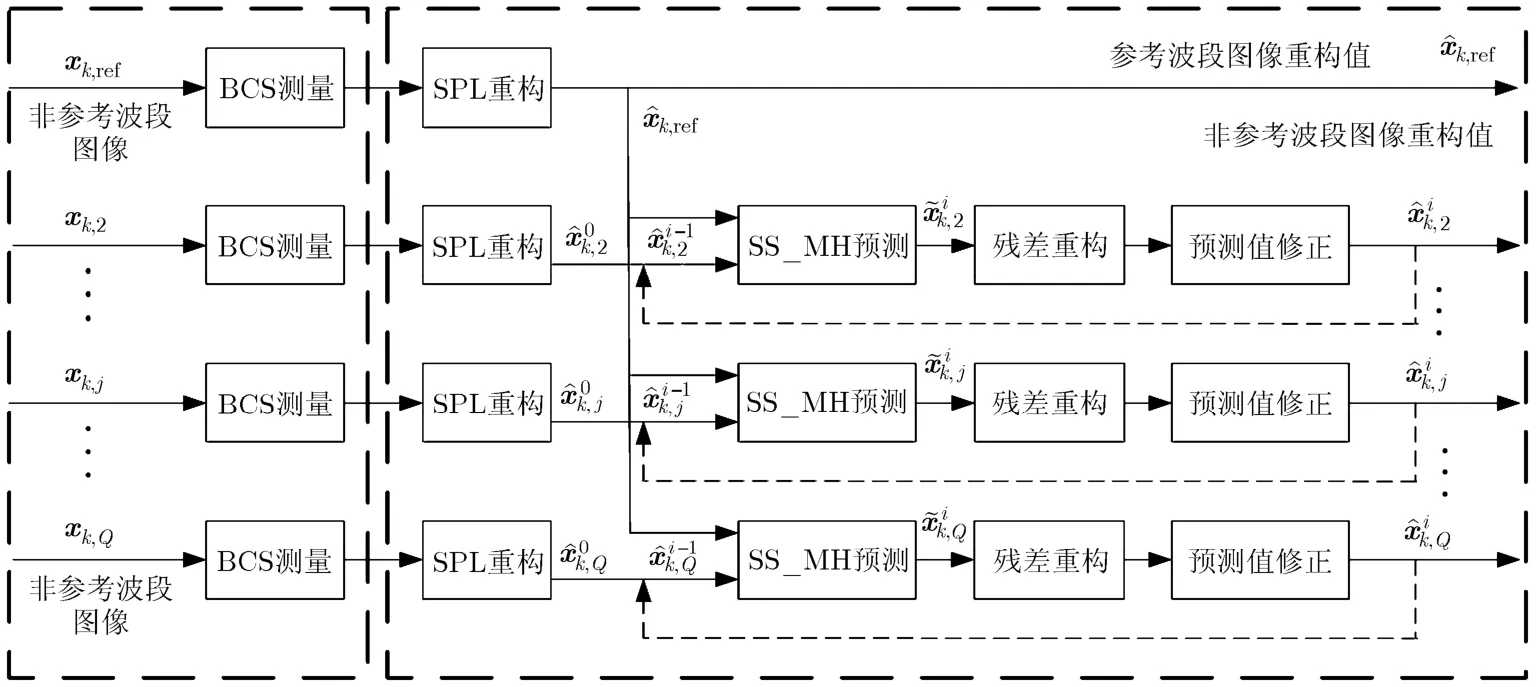
图1 SS_MH_BCS_SPL算法框图

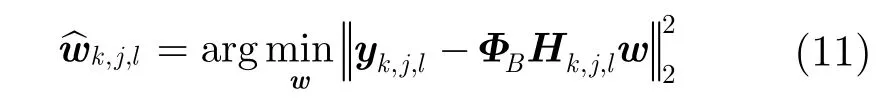
因此，实现多假设预测的关键是找到原始图像的预测候选集 P（xca），从而形成多假设预测矩阵Hk，j，l，求解权重系数后，获取预测值。获取预测值后，预测候选集和权重系数并不需要保留，可节省计算机的内存空间。

3.2 空谱联合的多假设预测模型

对于高光谱图像的每个波段图像来说，某一像素与其相邻像素具有相似性，不同图像块之间存在冗余信息，可利用目标像素的邻近像素对其进行预测，即利用空间相关性完成预测，预测残差应具有空间上的稀疏性。同时，高光谱图像是在连续光谱波段上对同一地物进行成像，相邻波段图像上的像素是同一地物对不同波段的反射，则同一空间位置的像素在不同波段的像素值之间具备相似性，波段越接近，相邻波段图像的谱间相关性越强，存在冗余信息较多，因此可利用相邻波段像素对目标像素进行预测，即利用谱间相关性完成预测，得到的残差应具备谱间稀疏性。利用高光谱图像的空间相关性和谱间相关性，引入空谱联合的多假设预测模型。

在高光谱图像分块压缩感知中，对图像块 xk，j，l进行预测时，由于不同图像块之间具有空间相关性，因此可用邻近图像块对当前图像块进行预测。对来说，其候选集中的预测值由其初始重构值中与 xk，j，l相邻的图像块组成。图像 xk，j的分块大小为B × B，选定搜索窗大小为b，则搜索在以当前图像块的中心为原点，以（B + 2b）/2为半径的图像方块内进行。当前图像块的预测候选集p（xca）由该搜索窗内每个大小为B × B的图像块组成，多假设预测图像块的形成过程如图2所示，每个图像块的列向量化表示组成预测矩阵。此处利用了图像的空间相关性，故所形成的预测矩阵标记为

因高光谱图像的光谱分辨率高，具有谱间相关性，因此，参考波段重构图像 xˆk，ref也能对非参考波段图像进行预测。当前图像块 xk，j，l的预测候选集由中与 xk，j，l相应位置及其邻近的图像块组成，搜索过程亦如图2所示，只是此处的搜索窗是在参考波段图像的重构值内。此处的预测矩阵利用了不同波段图像的谱间相关性，故预测矩阵标记为由于参考波段的重构图像具有一定的误差，会产生重构误差传递的影响，因此，在进行多假设预测时，不仅考虑参考波段的重构图像，而且考虑非参考波段的重构图像，两者结合组成候选预测集，可得到更精确的预测权重系数，从而降低单一预测集所带来的误差传递的影响。

同时利用空间和谱间相关性进行预测，得到空谱联合的多假设预测矩阵表示为

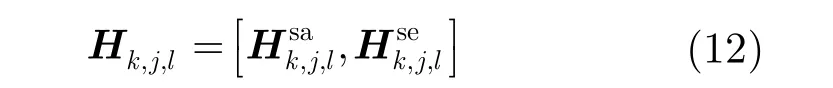
利用Tikhonov正则化方法［32］求解式（11）得到权重系数，为式（11）加入惩罚项，得到

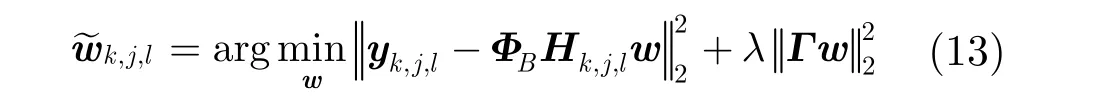
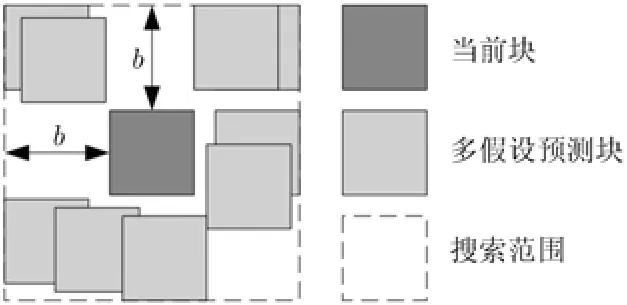
图2 多假设预测过程

其中，λ为拉格朗日因子，文中选择 λ= 0.0625，矩阵Γ是 Tikhonov矩阵，包含的先验信息是：与目标图像块越相似的图像块，其权重系数就越大，反之其权重系数就越小。Γ矩阵对角线上的值定义为：是矩阵的第d列， d= 1，2，…， D ，D是当前图像块 xk，j，l的候选预测集合中所有预测图像块的个数。

求解当前图像块的预测权重系数：

3.3 空谱联合的多假设预测重构算法

为充分利用高光谱图像的空间相关性和谱间相关性，本文提出空谱联合的多假设预测重构算法。将高光谱图像分组为参考波段图像和非参考波段图像，参考波段图像利用BCS_SPL算法进行重构。而非参考波段图像的基于空谱联合的多假设预测重构算法的主要过程为：（1）利用SPL算法得到非参考波段的初始重构图像（2）利用参考波段的重构图像和非参考波段的重构图像对非参考波段图像进行多假设预测，得到预测值， （3）对预测值采样，）与原图像的测量值进行求差，得到残差测量值（5）利用 SPL算法重构残差，（6）利用重构残差值对预测值进行修正，得到重构值

为保证重构图像的精度，算法中的多假设预测和残差重构需迭代进行。多假设预测搜索窗大小是否改变利用结构相似性（Structural SIMilarity，SSIM）［27］进行判定，同时利用交叉验证［28］计算重构算法终止迭代的判据参数。具体来说，每个波段图像的测量值 yk，j中需有3个测量值作为监测算法效果的测试集其他测量值用于重构。例如，采样率为0.1，分块大小为32时，测量矩阵应为 φB∈则用于重构的测量矩阵为而测试集的测量矩阵为即因此，利用测试集的测量矩阵得到残差在测量域中的值为

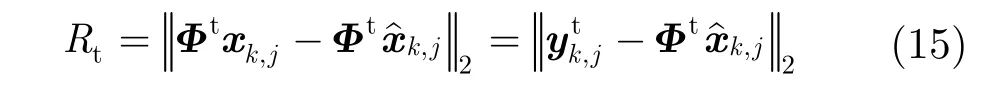
综上，算法SS_MH_BCS_SPL总结如表1所示（注：文中给出完整分组图像的重构过程，对于未能完全分组的图像，其计算方法与之相同）。

表1 SS_MH_BCS_SPL算法

4 实验结果与分析

选择4组高光谱图像进行实验。前两组数据来自AVIRIS的Cuprite矿区的Cuprite1和Cuprite2场景（http://aviris.jpl.nasa.gov），数据集共有 224个波段，波长范围为400～2500 nm，空间分辨率为20 m，图像大小为512×512。实验中，将波段图像大小截取为 256×256，同时，去除水汽吸收波段，可用波段数为188。第3组数据是由AVIRIS测得的Indiana西北部的植被地区Indian Pines，图像大小为145×145，波段数为220，波长范围为400～2500 nm。实验分块大小选择为 B= 32，为保证完整分块，将图像裁剪为128×128，且去除了20个水汽吸收波段。最后一组数据是由 ROSIS测得的意大利的Pavia大学地区Pavia University，数据包含115个波段，波长范围为 430～860 nm，空间分辨率高达1.3 m。为保证数据分块的完整性，数据裁剪至256×256，并去除12个含噪波段。4组高光谱数据第50个波段的原始图像如图3所示。

利用 SS_MH_BCS_SPL算法、不预测的BCS_SPL算法［30］、仅利用空间相关性进行预测的spatial_MH_BCS_SPL算法［27］以及仅利用谱间相关性进行预测的spectral_MH_BCS_SPL算法对4组高光谱图像进行压缩感知测量和重构，并利用重构图像的峰值信噪比（Peak Signal-to-Noise Rate，PSNR）来衡量算法性能。在采样端，4种算法均是单独对每个波段图像进行BCS采样，但在重构端，BCS_SPL算法对每个波段图像利用SPL算法进行重构；spatial_MH_BCS_SPL算法和 spectral_ MH_BCS_SPL算法分别利用空间相关性和谱间相关性对每个波段图像进行多假设预测，然后利用SPL算法进行预测残差重构。SS_MH_ BCS_SPL算法则在重构端同时利用空间和谱间相关性，完成每个非参考波段图像的多假设预测，最后采用SPL算法进行预测残差重构。

在采样过程中，BCS_SPL算法、spatial_MH_ BCS_SPL算法以及spectral_MH_BCS_SPL算法对每个波段图像的采样率均相同，而SS_MH_BCS_ SPL算法需将高光谱图像进行分组处理，并设定参考波段图像的采样率高于非参考波段图像，以充分利用参考波段图像的重构值提供精确的预测信息。因此，为保证算法比较的公平性，需保持平均采样率相同。假定平均采样率为S，参考波段图像的采样率为 Sref，非参考波段图像的采样率为 Snon-ref，将ΔS 作为采样率调节因子，即

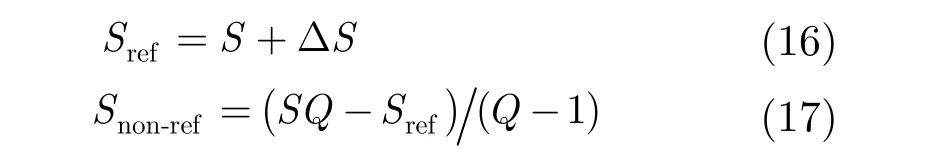
实验中选定分组大小为 Q= 8，平均采样率S取值范围为0.1～0.5，采样率调节因子 ΔS 的取值范围为 0.1～0.5，间隔均为 0.1。根据式（16）和式（17）计算得到的 Sref和 Snon-ref如表2所示。

从表2中可以看出，当 ΔS 增至0.5，平均采样率为0.5时，参考波段图像的采样率已等于1，此时图像已无法实现压缩；而当 ΔS 增至0.5，平均采样率为 0.1时，非参考波段图像的采样率较低，得到的初始重构图像精度也较低，无法提供精确的预测信息。综合上述两种情况，故下文讨论的 ΔS 的范围是0.1～0.4。

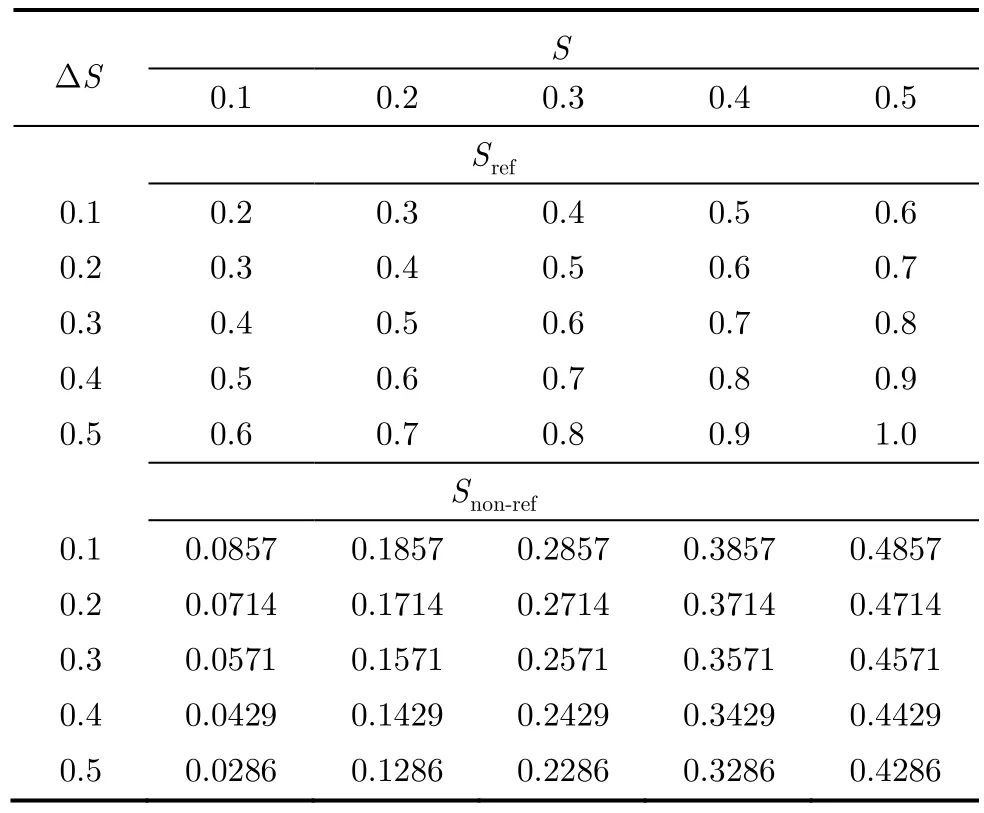
表2 不同调节因子 ΔS 下，参考波段图像和非参考波段图像的采样率

图3 4组高光谱数据的第50个波段的原始图像

利用算法SS_MH_BCS_SPL进行压缩感知测量和重构，其中多假设预测的搜索初始窗大小设定为b= 6，结构相似性的判定阈值设定为 τ= 0.0001。表3给出了不同高光谱重构图像的峰值信噪比，其中每组采样率下PSNR的最高值用黑体表示。当平均采样率较低如 S= 0.1时，4组图像的PSNR随着ΔS 的增大而下降，这是由于，此时非参考波段图像的采样率太低，利用SPL得到的重构图像的精度太低，导致最终的重构精度下降。而在平均采样率升高时，重构图像的PSNR随着 ΔS 的增大而增加。这是因为，随着参考波段图像采样率的增加，其重构精度提高，为非参考波段图像提供的预测信息更加准确，同时非参考波段图像的采样率也有所增加，其初始重构图像的精度也相对增加，两者的联合最终提高了非参考波段图像的重构精度。由于算法在ΔS = 0.4时的重构精度最高，故下文中的 SS_ MH_BCS_SPL算法均指 ΔS = 0.4的情况。

表3 不同调节因子 ΔS 下，算法SS_MH_BCS_SPL重构图像的平均峰值信噪比

利用不同算法对4组高光谱图像进行压缩感知重构，不同平均采样率下重构图像的PSNR曲线对比如图4～图7所示。从图中可以看出，单独利用空间相关性或谱间相关性进行预测的 spatial_ MH_BCS_SPL算法和spectral_MH_BCS_SPL算法均优于每个波段图像单独重构的BCS_SPL算法，但其PSNR提高的范围有限，最高可达1 dB左右。算法SS_MH_BCS_SPL不仅利用每个波段相邻图像块之间的空间相关性，而且利用不同波段图像之间的谱间相关性，算法性能最优。特别是对Cuprite2场景来说，无论是利用空间相关性还是谱间相关性均无法显著提高重构图像的精度，而算法SS_MH_BCS_SPL却能在高采样率下提高其重构图像的PSNR，提高幅度在2 dB以上，进一步证明了该算法的优越性。在低采样率下，所提算法优势不明显，原因在于此时非参考波段图像自身的采样率非常低，其初始重构值的精度太低，无法提供准确的预测信息，仅利用参考波段图像的重构值所能得到的预测信息并不精确，因此最终的重构精度不如预期的精度高，但仍优于不预测和单独利用空间或谱间相关性进行预测的重构算法。

平均采样率 S= 0.2下，采用 4种算法得到的Cuprite2场景的第50个波段（该波段图像为非参考波段图像）的重构图像如图8所示。从图中可以看出，利用BCS_SPL算法、spatial_MH_BCS_SPL算法和spectral_MH_BCS_SPL算法所得的重构图像精度较低，而SS_MH_BCS_SPL算法不仅利用图像的空间相关性，而且利用了相邻波段图像之间的谱间相关性，得到的重构图像PSNR较高，说明联合空间相关性和谱间相关性的预测方法有益于高光谱重构图像精度的提高。

图4 不同算法得到的Cuprite1场景重构图像的PSNR

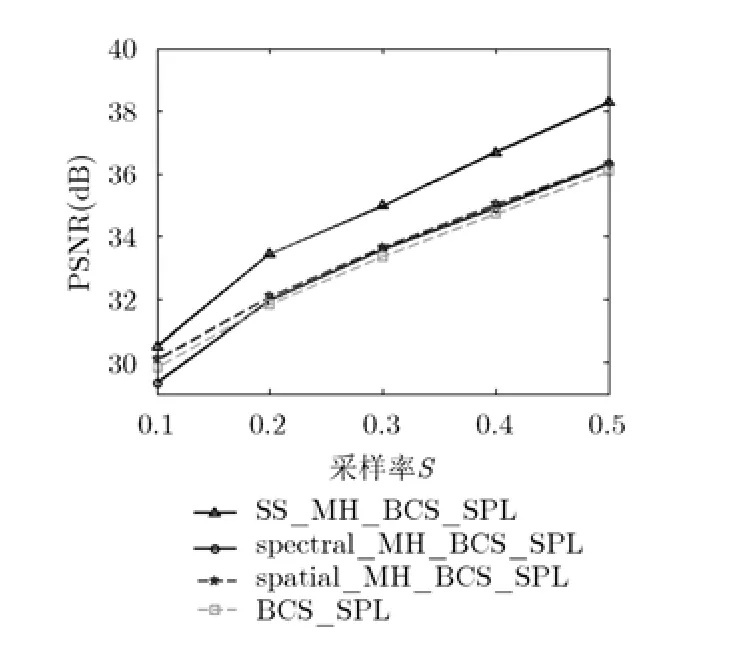
图5 不同算法得到的Cuprite2 场景重构图像的PSNR

图6 不同算法得到的Indian Pines场景重构图像的PSNR

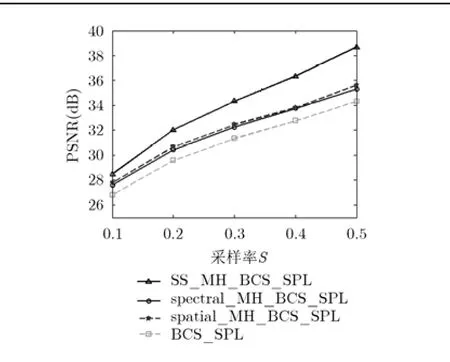
图7 不同算法得到的Pavia University 场景重构图像的PSNR

图8 不同算法在平均采样率为 S= 0.2下得到的Cuprite2场景的重构图像对比

5 结束语

本文针对如何利用高光谱图像的空间和谱间相关性提高压缩感知重构图像的精度问题，提出基于空谱联合的多假设预测压缩感知重构算法。利用参考波段图像和非参考波段图像的重构值，引入空谱联合的多假设预测模型，完成对非参考波段图像的多假设预测，并利用重构的预测残差修正预测值，通过迭代方式提高重构精度。实验结果表明，所提重构算法优于仅利用空间相关性或谱间相关性进行预测的重构算法和不预测的重构算法，在平均采样率一定时，其重构图像的精度最高。

［1］ Heras D B， Argüello F， and Quesada-Barriuso P. Exploring ELM-based spatial-spectral classification of hyperspectral images［J］. International Journal of Remote Sensing， 2014，35（2）: 401-423.

［2］ Zhao C， Li X， Ren J， et al.. Improved sparse representation using adaptive spatial support for effective target detection in hyperspectral imagery［J］. International Journal of Remote Sensing， 2013， 34（24）: 8669-8684.

［3］ Tan C， Samanta A， Jin X， et al.. Using hyperspectral vegetation indices to estimate the fraction of photosynthetically active radiation absorbed by corn canopies［J］. International Journal of Remote Sensing， 2013，34（24）: 8789-8802.

［4］ Xie X， Li Y， Li R， et al.. Hyperspectral characteristics and growth monitoring of rice （Oryza sativa） under asymmetric warming［J］. International Journal of Remote Sensing， 2013，34（23）: 8449-8462.

［5］ Donoho D. Compressed sensing［J］. IEEE Transactions on Information Theory， 2006， 52（4）: 1289-1306.

［6］ Candès E， Romberg J， and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information［J］. IEEE Transactions on Information Theory， 2006， 52（2）: 489-509.

［7］ Provost J and Lesage F. The application of compressed sensing for photo-acoustic tomography［J］. IEEE Transactions on Medical Imaging， 2009， 28（4）: 585-594.

［8］ Riccardo M， Giorao Q， Michele R， et al.. A Bayesian analysis of compressive sensing data recovery in wireless sensor networks［C］. International Conference on Ultra Modern Telecommunications&Workshops， St. Petersburg， 2009: 1-6.［9］ Shu X and Ahuja N. Imaging via three-dimensional compressive sampling［C］. Paper presented at the International Conference on Computer Vision （ICCV），Barcelona， ES， 2011: 439-446.

［10］ 沈志博， 董春曦， 黄龙， 等. 基于压缩感知的宽频段二维DOA估计算法［J］. 电子与信息学报， 2014， 36（12）: 2935-2941. Shen Zhi-bo， Dong Chun-xi， Huang Long， et al.. Broadband 2-D DOA estimation based on compressed sensing［J］. Journal of Electronics & Information Technology， 2014， 36（12）: 2935-2941.

［11］ 王军， 闫锋刚， 马文洁， 等. 基于Laplace先验的Bayes压缩感知波达方向估计［J］. 电子与信息学报， 2015， 37（4）: 817-823. Wang Jun， Yan Feng-gang， Ma Wen-jie， et al.. Direction-of-arrival estimation using Laplace prior based on bayes compressive sensing［J］. Journal of Electronics & Information Technology， 2015， 37（4）: 817-823.

［12］ Yin J， Sun J， and Jia X. Sparse analysis based on generalized Gaussian model for spectrum recovery with compressed sensing theory［J］. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing， 2015， 8（6）: 2752-2759.

［13］ Candès E and Tao T. Decoding by linear programming［J］. IEEE Transactions on Information Theory， 2005， 51（12）: 4203-4215.

［14］ Figueiredo M， Nowak R D， and Wright S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems［J］. IEEE Journal of Selected Topics in Signal Processing， 2007， 1（4）: 586-598.

［15］ Baron S， Sarvoham R， and Baraniuk R G. Bayesian compressive sensing via belief propagation［J］. IEEE Transactions on Signal Processing， 2010， 58（1）: 269-280.

［16］ Mallat S G and Zhang Z. Matching pursuits with timefrequency dictionaries［J］. IEEE Transactions on Signal Processing， 1993， 41（12）: 3397-3415.

［17］ Fowler J E. Compressive-projection principal component analysis［J］. IEEE Transactions on Image Processing， 2009，18（10）: 2230-2242.

［18］ Gan L. Block Compressed sensing of natural images［C］. 15th International Conference on Digital Signal Processing，Cardiff， Wales， UK， 2007: 403-406.

［19］ Ji S， Dunson D， and Carin L. Multitask compressive sensing［J］. IEEE Transaction on Signal Processing， 2009，57（1）: 92-106.

［20］ Claudia V C， Henry A， and Gonzalo R A. Fast lapped block reconstructions in compressive spectral imaging［J］. Applied Optics， 2013， 52（10）: D32-45.

［21］ Henry A， Hoover R， Wu Y， et al.. Higher-order computational model for coded aperture spectral imaging［J］. Applied Optics，2013， 52（10）: D12-21.

［22］ 刘海英， 吴成柯， 吕沛， 等. 基于谱间预测和联合优化的高光谱压缩感知图像重构［J］. 电子与信息学报， 2011， 33（9）: 2248-2252. Liu Hai-ying， Wu Cheng-ke， Lü Pei， et al.. Compressed hyperspectral image sensing reconstruction based on interband prediction and joint optimization［J］. Journal of Electronics & Information Technology， 2011， 33（9）: 2248-2252.

［23］ 刘海英， 李云松， 吴成柯， 等. 一种高重构质量低复杂度的高光谱图像压缩感知［J］. 西安电子科技大学学报（自然科学版），2011， 38（3）: 37-41. Liu Hai-ying， Li Yun-song， Wu Cheng-ke， et al.. Compressed hyperspectral image sensing based on interband prediction［J］. Journal of Xidian University （Natural Science）， 2011， 38（3）: 37-41.

［24］ Mun S and Fowler J E. Residual reconstruction for blocked-based compressed sensing of video［C］. Paper presented at the Data Compression Conference （DCC），Snowbird， UT， 2011: 183-192.

［25］ 李然， 干宗良， 崔子冠， 等. 联合时空特征的视频分块压缩感知重构［J］. 电子与信息学报， 2014， 36（2）: 285-292. Li Ran， Gan Zong-liang， Cui Zi-guan， et al.. Block compressed sensing reconstruction of video combined with temporal-spatial characteristics［J］. Journal of Electronics & Information Technology， 2014， 36（2）: 285-292.

［26］ 贾应彪， 冯燕， 袁晓玲， 等. 高光谱图像分块压缩感知采样及谱间预测重构［J］. 应用科学学报， 2014， 32（3）: 281-286. Jia Ying-biao， Feng Yan， Yuan Xiao-ling， et al.. Block compressed sensing sampling and reconstruction using spectral prediction for hyperspectral images［J］. Journal of Applied Science， 2014， 32（3）: 281-286.

［27］ Chen C， Tramel E W， and Fowler J E. Compressed-sensing recovery of images and video using multihypothesis predictions［C］. Proceedings of the 45th Asilomar Conference on Signals， Systems， and Computers， Pacific Grove， CA， 2011: 1193-1198.

［28］ Chen C， Li W， Tramel E W， et al.. Reconstruction of hyperspectral imagery from random projections using multihypothesis prediction［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（1）: 365-374.

［29］ Fowler J E， Mun S， and Tramel E W. Block-based compressed sensing of images and video［J］. Foundations and Trends in Signal Processing， 2012， 4（4）: 297-416.

［30］ Mun S and Fowler J E. Block compressed sensing of images using directional transforms［C］. Paper presented at the International Conference on Image Processing （ICIP）， Cairo，EG， 2009: 3021-3024.

［31］ Johnson W B and Lindenstrauss J. Extensions of Lipschitz mappings into a Hilbert space［J］. Contemporary Mathematics，1984， 26（1）: 189-206.

［32］ Tikhonov A N and Arsenin V Y. Solutions of Ill-posed Problems［M］. Washington， DC， USA: V. H. Winston & Sons，1977: 45-87.

王 丽： 女，1987年生，博士生，研究方向为压缩感知、高光谱图像处理与优化算法设计.

冯 燕： 女，1963年生，教授，博士生导师，研究方向为高光谱数据分析、数据压缩、神经网络和压缩感知及其应用等.

Compressed Sensing Reconstruction of Hyperspectral Images Based on Spatial-spectral Multihypothesis Prediction

Wang Li Feng Yan
（Department of Electronics Engineering， Northwestern Polytechnical University， Xi’an 710129， China）

Compressed Sensing （CS） reconstruction of hyperspectral images driven by spatial-spectral multihypothesis prediction is proposed in order to take full advantage of spatial and spectral correlation of hyperspectral images. The hyperspectral images are grouped into reference band images and non-reference band images， and the reference band images are reconstructed by Smoothed Projected Landweber （SPL） algorithm. For the non-reference band images， the spatial-spectral multihypothesis prediction model is introduced to improve the reconstruction accuracy. Multihypothesis predictions drawn for an image block of non-reference band image are made not only from spatially surrounding image blocks within an initial non-predicted reconstruction of non-reference band image， but also from the corresponding position and neighboring image blocks within the reconstruction of reference band image. The resulting predictions are used to generate residuals in the projection domain， and the residuals are reconstructed to revise the prediction values. The residuals being typically more compressible than the original images and the iterative execution mode lead to improved reconstruction quality. Tikhonov regularization is utilized to solve the weight coefficients of multihypothesis prediction and structural similarity is used as a criterion to decide whether to change the search window size or not. Cross validation is presented to compute the criterion parameter of iteration termination. Experimental results demonstrate that the proposed algorithm outperforms alternative strategies only using spatial correlation or spectral correlation to predict or not employing prediction and the peak signal-to-noise ratio of its reconstructed images is increased by more than 2 dB.

Hyperspectral image； Compressed Sensing （CS）； Spatial-spectral multihypothesis prediction； Tikhonov regularization； Structural similarity

s: The National Natural Science Foundation of China （61071171）； The Doctorate Foundation of Northwestern Polytechnical University （CX201424）

TP751

A

1009-5896（2015）12-3000-09

10.11999/JEIT150480

2015-04-28；改回日期：2015-08-21；网络出版：2015-11-01

*通信作者：冯燕 sycfy@nwpu.edu.cn

国家自然科学基金（61071171）和西北工业大学博士论文创新基金（CX201424）