c-可补子群对有限群结构的影响
潘 虹, 周 强
(信阳师范学院 数学与信息科学学院, 河南 信阳 464000)
0 引言
利用子群的可补性来研究有限群的结构已经有很多结果.例如,利用某些特殊子群的可补性质可得到有限群的可解性[1-4].最近Ballester-Bolinches和Guo[5]证得了具有初等交换Sylow子群的所有有限超可解群所在的群类恰好就是每个极小子群都可补的所有有限群所在的群类.
本文在文献[5]的基础上,利用子群c-可补的概念及性质,在较弱的条件下讨论群的幂零性.用符号Gp来表示G的Sylowp-子群,除此之外,本文中所采用的其他记号都是标准的,所涉及的群都是有限群.
1 预备知识
定义1[6]设G为有限群,H≤G,称H在G中c-可补,如果存在G的一个子群K使得G=HK且H∩K≤HG,其中HG=∩g∈GHg为包含在H中的G的最大正规子群.
引理1[6]设G为有限群,则
(1)如果H在G中c-可补且H≤K≤G,那么H在K中c-可补.

(3)令π是一个素数集合.设N为G的一个正规π′子群且H为G的一个π子群.如果H在G中c-可补,那么HN/N在G/N中c-可补.而且若N正规化H,那么反之也成立.
引理2[7]设G为内幂零群,则
(1)G的阶为pαqβ且p≠q;

(3) 若P为Abel群,则P为初等Abel群;
(4) 当p≠2时,expP=p;当p=2时,expP≤4, 其中expP表示群P的指数;
(5)c∈P为P的生成元的充要条件是c与a不可换;
(6)Z(G)=Φ(G)=Φ(P)×Φ(Q).
引理3[8]设G是内超可解群,则G有如下结构:
(1) 存在正规子群P∈Sylp(G),使得G=P×M,P/Φ(P)是G/Φ(P)的极小正规子群;
(2) 若p>2,则expP=p;若p=2,则expP≤4且p2/|G|;
(3) 存在c∈PΦ(P),使〈c〉不正规于G;
(4) 若P为Abel群,则Φ(P)=1;
(5) 若P非交换,则Φ(P)=Z(P)=P′;
(6)G为Sylow塔群或G为幂零群.
2 主要结果
定理1 如果群G的每一素数阶子群在Z(G)中,且G的4阶循环子群在G中c-可补,则G为幂零群.
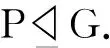
注1 本定理用G的4阶循环子群的c-可补性代替G的4阶子群的c-正规性推广了文献[6]中的定理1,因为c-正规子群一定是c-可补子群,但反之不一定成立.

证明假设定理不真,选取G为极小阶反例.
(1)定理条件是子群遗传的.
事实上,设H (2)素数p只能等于2. 若不然,p>2,由引理2(4)知,expP=p,从而由条件知P∩N≤Z(G).又由引理2及条件知G/P∩N≅/G×G/N幂零,从而G/Z(G)为幂零群,G为幂零群,矛盾.故素数p只能等于2. (3)导出矛盾. i) 当N=G时,由定理1知G为幂零群,矛盾.同样当N=1时,由条件得G为幂零群,也矛盾. 定理3 如果群G的每个素数阶子群在Z(G)中,且G的4阶循环子群在G中c-可补,则G为幂零群. 证明假设定理不真,选取G为极小阶反例. 1) 定理条件是子群遗传的. 事实上,对G的任意真子群H,K为H的p阶子群,则K≤Z(G)∩H≤Z(H).由引理1(1)知H的子群在H中c-可补.所以H满足定理条件,由G的取法知,H为幂零群,故G为内幂零群,即G=PQ,这里P和Q满足引理2的条件. 2) 素数p只能等于2,从而G=2αqβ. 若不然,p>2,则由引理3(4)知expP=p,由条件知P≤Z(G).由文献[3]中定理VI.2知Z(G)幂零.从而G=PQ=Z(G)幂零,矛盾. 3)G为超可解群. 若不然,必为内超可解群.我们断定:对任意的a∈PΦ(P)有|a|=4.事实上,若存在a∈PΦ(P)使|a|=2,设〈x〉为G的Sylowq-子群,令 M=〈a,ax,…,aqb-1〉≤P, 由引理3(1)知P/Φ(P)是G/Φ(P)的极小正规子群,从而P=MΦ(P)=M.因为axqi∈Z(G),1≤i≤b,所以P≤Z(G),于是由G/P为幂零群知,G/Z(G)为幂零群,从而G为幂零群,矛盾.这样对任意的x∈PΦ(P),|x|=4,由条件〈x〉在G中c-可补,同样由定理1的证明〈x〉≤NG(Q),又Z(G)=Φ(G)=Φ(P)×Φ(Q),故对x∈Φ(P),则x∈Z(G),从而x∈NG(Q).这样对任意的x∈P都有x∈NG(Q),从而矛盾. 证明仿照定理2和3易证.证毕. 本文利用有限群中某些特殊子群的c-可补性质,主要研究有限群的幂零性和p-幂零性,一些相关的结果得到了推广.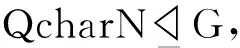
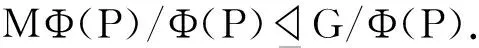

3 结论

