引发认知冲突 促进概念理解

吴瑞英

[摘 要]数学教学中，教师应以学生的认知为切入口，设置符合学生实际的认知冲突，激发学生的学习动机与需求，使每位学生都深刻理解所学知识。

[关键词]数学教学 认知冲突 概念 理解 促进

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）20-043

“认识分数”既是教学分数的第一课时，又是学生学习分数概念的起始课。因此，教师在教学中要根据学生的认知特点，合理设置认知冲突，促进学生对概念的理解，这对学生掌握分数的本质至关重要。

一、创设情境，感知概念

学生学习数学是从自己的生活实践开始的，因此教师可以创设贴近学生生活的情境，激发学生的探求欲，引导学生通过观察、想象等活动，逐步感知概念。

教学片断：

师：刚才我们很顺利地把四个苹果和两瓶水进行了平均分，那你们会分蛋糕吗？

生1：我会平均分，要公平，每人一半。

师：每人一半，大家同意这位同学的意见吗？（同意）那“一半”如何用数来表示呢？（学生讨论）

生2：老师，“一半”可以用二分之一来表示。

师：二分之一？请你上来写一写。（生上台板书1 / 2）

师：这个二分之一，我们以前没接触过呀！那你知道1 / 2是什么意思吗？

……

反思：上述教学中，教师先唤醒学生已有的平均分知识，使学生的思维顺着平均分很自然地想到把一个蛋糕平均分才公平，这样就将分数最本质的特征“平均分”在不露痕迹中让学生感知了。“那‘一半’如何用数来表示呢”，这是学生认知的第一次冲突，从自然数到分数，既是对数的扩充，也是学生认识自然数后的一次知识“生长”。学生尝试用数来表示“一半”，从而经历了一个思考、创造的过程，对分数的初步感知会更加深刻。

二、动手操作，深化概念

小学生学习数学的过程，就是自己“做”数学的过程。为了帮助学生深化对概念的认知，可将形成分数概念的过程变为在尝试操作下的思考与分析的过程。

教学片断：

师：拿一张长方形纸折一折，并把它的1 / 2涂上颜色。（学生先动手操作，再交流展示不同的折法：一是沿两条长的中心对折；二是沿两条宽的中心对折；三是沿对角线对折）对这三种不同的折法，你有什么想说的？

生1：我觉得这三种折法都对，都是表示这个长方形的1 / 2。

生2：我也觉得是对的，只是好像有什么不同的地方。

师：什么地方不同呀？

生3：平均分后的形状不同。

师：平均分后的形状不同，为什么都可以用1 / 2来表示？

生4：虽然形状不同，但它们都是把长方形纸平均分成两份，一份就是它的1 / 2。

……

反思：上述教学中，教师先让学生自己动手折，展示不同的折法，再让学生自主探索，并对结果进行思辨，从而产生第二次认知冲突——“为什么形状不同，都可以用1 / 2来表示”。“虽然形状不同，但它们都是把长方形纸平均分成两份，一份就是它的1 / 2”，学生此时对分数的本质属性的认识就有了一个质的飞跃。

三、变式比较，内化概念

“形成数学概念的标志就是掌握对象的内涵与外延。”课堂教学中，教师要通过呈现不同的变式，引导学生从拓展分数的外延来内化概念的内涵，为学生顺利、正确掌握分数的概念打下基础。

教学片断：

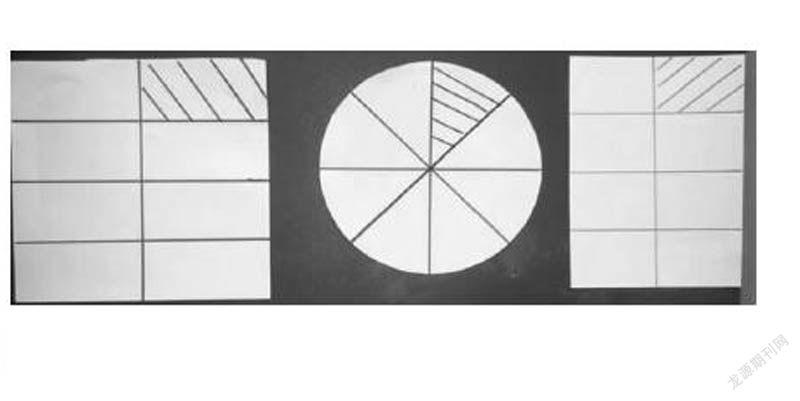
师（出示右图）：同学们，对于这幅作品，你有什么想说的？

生1：这幅作品都是把每个图形平均分成8份，一份就是1 / 8。

师：不同图形都可以得到1 / 8，这说明什么？

生2：说明分数的得出不是看图形，而是看平均分的份数。

……

反思：经验有时对概念的学习会产生消极的负效应。上述教学中，教师针对学生的思维定式，引导学生用不同图形折出相同的分数来拓展分数的外延，创设第三次认知冲突——“不同图形都可以得到1 / 8，这说明什么”，为学生形成正确的概念做好知识的铺垫。

总之，教师在教学中应以学生的认知为切入口，设置符合学生实际的认知冲突，激发学生的学习动机与需求，使每位学生都深刻理解所学知识。

（责编 杜 华）