基于流体逼近的路段交通流动态加载研究

纪翔峰，张健，冉斌*

（1.东南大学城市智能交通江苏省重点实验室，南京210096；2.现代城市交通技术江苏高校协同创新中心，南京210096）

基于流体逼近的路段交通流动态加载研究

纪翔峰1，2，张健1，2，冉斌*1，2

（1.东南大学城市智能交通江苏省重点实验室，南京210096；2.现代城市交通技术江苏高校协同创新中心，南京210096）

路段交通流动态加载是动态交通网络分配模型中的重要组成部分，在路段交通流动态加载中，离散形式或者连续形式的点排队模型被广泛使用.本文在以往研究的基础上，提出基于流体逼近的连续型点排队模型，克服了原有点排队模型中排队负值的情况.通过分析可以发现，原有点排队模型实质上属于具有单一服务台和无限容量的排队模型，基于流体逼近的思想重新定义了原有点排队模型.其中3个主要部分是流量守恒模型，车辆流出模型和时间相关的服务台模型，这3个模型全部都是连续的.由于连续点排队对计算需求较高，本文将连续的排队模型离散化，模拟了3种不同场景下车辆驶出、路段排队情况.本文模型克服了原有点排队中的负排队现象，并且排队过程满足先进先出的原则，模型具有良好的模拟效果.

交通工程；连续点排队模型；排队系统；流体逼近；离散化；非负排队；先进先出

1 引言

在最近的几十年中，动态交通分配模型被广泛的进行研究，并且被应用于实时的交通管理，如可变信息板等.其中，出行路径选择和交通流动态加载是动态交通分配的两个主要的组成部分.本文的研究就是基于交通流动态加载展开的.在交通流的动态加载中，Vickrey的点排队[1]模型被广泛的采用[2-6]，但是该模型最大的问题是会出现排队为负值的情形[2，3].对于该问题，国外的学者进行了相关的研究.Nie等[3]将点排队模型离散化，提出一种改进的点排队模型克服了负排队的现象.Ban等[4]深入分析了点排队模型，提出两种不同的改进方式，一种是通过线性互补方程的形式，一种是提出了所谓的α-模型.Han等[5]通过引入虚拟的空间维变量，将原有的点排队模型描述成为质量守恒的形式.Ji等[6]提出一种基于流体逼近的连续型点排队模型，克服了原有点排队模型中出现非负排队的情形.

本文在以往研究的基础上，进一步分析了基于流体逼近的点排队模型在路段交通流动态加载过程中的非负排队及先进先出行为.本文首先对基于流体逼近的连续型点排队模型进行回顾，在之前的研究中，求解点排队模型的Runge-Kutta算法的计算需求较大，本文提出对基于流体逼近的点排队模型进行Backward离散化，并且采用Backward离散化的模型研究了路段排队的非负性和路段交通流动态加载过程中的先进先出行为.通过研究发现，Backward离散化的模型同样克服了原有点排队模型中出现负排队的情形，并且路段交通流动态加载过程中满足先进先出的原则，具有良好的模拟效果.

2 Vickrey的点排队模型

原有的点排队模型主要由以下集计变量组成：

（1）路段的自由流行驶时间t0和路段的通行能力；

（2）假设所有车辆的长度可以忽略，在路段的下游处进行排队，排队长度为q(t)；

（3）路段流量的变化情况由排队长度的变化情况来反应；

（4）路段的旅行时间τ(t)由路段的排队长度与路段通行能力的比值来确定.

p(t)和v(t)分别表示在时刻t路段的驶入流率和路段的驶出流率，具体的点排队的模型如下所示：

(1)排队长度的改变为

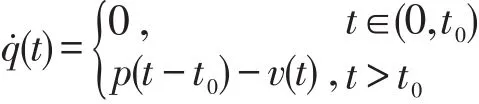
(2)初始长度为0，即q(t0)=0.

(3)如果t＜t0，路段的驶出流率为0，即v(t)=0.

(4)如果t＞t0，路段的驶出流率为

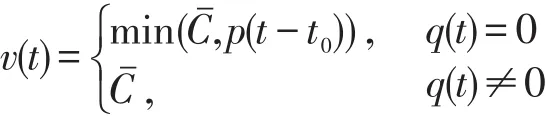
(5)如果t∈[0,T-t0]，路段的旅行时间为τ(t)=t0+()-1q(t+t0).

3 模型构建

原有的点排队模型会出现负排队的现象，国外有部分学者对此进行了研究，本文在之前研究的基础上，首先对基于流体逼近的点排队模型进行了回顾.通过观察可以发现，点排队模型实际上为单一的服务台、容量无限的排队模型，如图1所示.到达服务台的车辆实际上是非均匀到达，也就是车辆的到达率是时变的，并且到达服务台的时间与车辆驶入路段的时间之间存在固定的时间延误，也就是路段的自由流时间.服务台的服务效率是固定的，也就是路段的通行能力.当服务台的使用率不同时，路段的驶出量也不同.

图1 点排队模型的排队表示Fig.1 The queue form of point queue model

3.1 流量守恒函数

根据流量守恒原则，路段排队长度的变化率等于车辆到达率和离开率的差值.本文用fin(t)表示时刻t车辆的到达率；fout(t)表示时刻t车辆的离开率；t0表示路段自由流时间.排队长度的变化率可以表示为

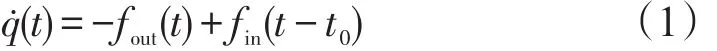
3.2 流量驶出函数和服务台使用率函数

本文将服务台使用率定义为路段驶出量与路段通行能力的比值.

利用服务台使用率函数，路段的流出率fout(t)可以表示为fout(t)=ρ(t).在点排队模型中，车辆的尺寸被忽略，也就是说排队空间是无限的，也就是服务台的缓冲区是无限容量的.因此，车辆的驶入率就是车辆的到达率，fin(t-t0)=p(t-t0).利用流量驶出函数和服务台使用率函数，流量守恒函数可以表示为(t)=-ρ(t)+p(t-t0).其中，ρ(t)会随着排队系统具体形式的不同而不同.一般来说，确定ρ(t)的具体形式较为困难，因此，本文采用Wang等[7]流体逼近的思想.利用流体逼近，(t)=-ρ(t)+p(t-t0)可以表示成为

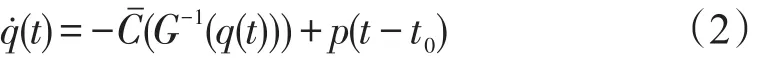
3.3 基于流体逼近的点排队重新解释

基于上述流体逼近模型，原有的点排队模型可以被重新解释为：

（1）排队长度的变化.

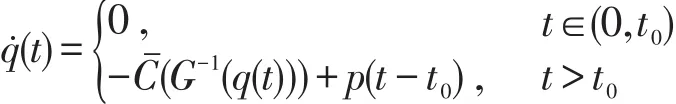
（2）初始排队长度为0，即q(t0)=0.

（3）如果t＜t0,驶出流率为0，即v(t)=0.

实际上，在流体逼近模型中的表现形式为ρ(t)=0.

（4）如果t＞t0，驶出流率为v(t)=ρ(t).

（5）如果t∈[] 0,T-t0，路段的实际旅行时间为

3.4 离散形式

在利用上述连续形式的点排队模型进行模拟过程中，如果将时间离散化为固定长度的时间间隔，在计算每个时间间隔结束时刻的排队长度时，需要采用Runge-Kutta[6-8]数值计算方法，计算时间较长.因此，基于上述连续型点排队模型，本文将其进行离散化，提出一种离散形式的流体逼近模型.该模型计算速度快，能够适用动态交通分配的需求，这也为未来研究中的拓展提供了良好的条件.本文采用流体逼近模型对点排队模型进行重新解释，得到了具有跳跃点的常微分方程（3.3节），离散后得到的模型也具有跳跃点，而这类模型的相关性质在数学理论上也较难探讨.因此，本文选取了Backward的离散形式，并且选取较小的离散步长，尽可能的确保收敛性，相应问题Ban等[4]也做了探讨.

在离散化的过程中，假设时间步长为Δ，自由流时间t0=mΔ，在不引起歧义的情况下，下述离散型的模型中，tΔ表示第t个时间步长.利用上述参数，本文对连续型的流体逼近重新进行了定义，具体如下：

（1）流量守恒函数.

（2）流量驶出函数.

基于上述离散型的流体逼近模型，原有的点排队模型可以被重新解释为：

（1）排队长度的变化.

（2）初始排队长度为0，即q(mΔ)=0.

（3）如果tΔ＜mΔ,驶出流率为0，即v(tΔ)=0.

实际上，在流体逼近模型中的表现形式为ρ(tΔ)=0.

（5）如果tΔ∈[] 0,TΔ-mΔ，路段的实际旅行时间为τ(tΔ)=mΔ+(ρ((t+m)Δ))-1q((t+m)Δ).

4 算例分析

假设路段车辆到达服从泊松分布，在路段车辆的离去模型中，选取3种不同的分布，分别是确定型分布（D），Erlang分布（Ek）和指数型分布（M），得到连续型流体逼近模型如表1所示，同时得到连续型模型所对应的离散型流体逼近模型如表2所示.在表1和表2中表示的是服务时间分布变异系数的平方.在本文中，服务时间指的是路段的流出率.

表1 不同离去模型下的流体逼近模型(连续状态)Table 1Different fluid approximation models with different exit models(continuous form)

表2 不同离去模型下的流体逼近模型（离散状态）Table 2Different fluid approximation models with different exit models(discrete form)

采用离散型模型对3种不同的流率进行模拟，时间步长为Δ=30 s，路段的通行能力为1 000.值得注意的一点是，假设路段的到达和离去分别服从一定的概率分布，而所构建的流体逼近模型就是将这种随机性关系转变为确定性关系.也就是说，用确定性的结果去逼近随机的概率分布，而不同输入和输出的随机性体现在不同流体逼近公式的参数和函数形式中，如表1和表2所示.本文具体的流入率如下：

路段的自由流行驶时间t0为60 min，模拟的时长为550 min.在第1种情形下，从第0 min到第180 min，路段的流入率为2 000 pcu/h，然后在第180 min时，存在间断点，流入率突然变为0，能够模拟现实交通中交通管制或者交通事故等现象；第2种情形是梯形的流入率，从第60 min到第120 min存在峰值，流入率为1 200 pcu/h，其他时段内流入率的改变为线性形式，能够模拟现实交通状况中早晚高峰的情形；第3种情形的流入率为sigmoidal曲线的形式，在这种流入率的情况下，当交通量较高时，流入量的波动不大，当交通量降低时，流入量的波动较大.

在作者先前的研究中，采用的是Runge-Kutta进行计算，对比本文的结果和先前已有的结果[6]，我们可以发现偏差较小.在先前的研究中，主要分析了非负排队的问题，本文在已有工作的基础上进一步分析先进先出问题.

本文首先对路段的排队长度和流出量进行模拟，模拟的结果如图3～图5所示.通过模拟结果可以发现，路段中排队为非负排队，克服了原有点排队模型中负排队的现象，因此，所得的路段流出量也为非负值.除此之外，从模拟结果可以发现，3种不同的排队所得的结果差别不大，这为后期交通分配中模型的选择提供了参考.在本文的模拟中，之所以3种模型的模拟结果差别不大，这是因为3种模型的路段使用率差别不大，如图2所示.此处的路段使用率分别是表2所示.

图2 三种流体逼近模型下的路段使用率对比Fig.2 Comparison of the link utilization ratio for the three models

图3 流入率#1下的排队长度和流出量Fig.3 Queue length and exit flow under inflow rate#1

图4 流入率#2下的排队长度和流出量Fig.4 Queue length and exit flow under inflow rate#2

路段交通流加载过程中，车辆是否满足先进先出可以通过路段旅行时间的改变率反映，因此，本文对路段的旅行时间和旅行时间改变率进行模拟，模拟结果如图6～图8所示.其中，路段旅行时间τ的计算公式如式（3）所示，路段旅行时间改变率Λτ的计算公式如式（4）所示.

图5 流入率#3下的排队长度和流出量Fig.5 Queue length and exit flow under inflow rate#3

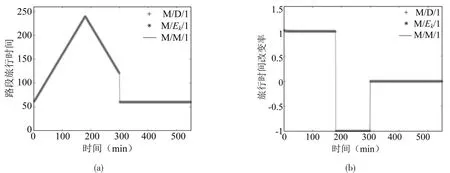
图6 流入率#1下的路段旅行时间及其改变率Fig.6 Link travel time and its change rate under inflow rate#1

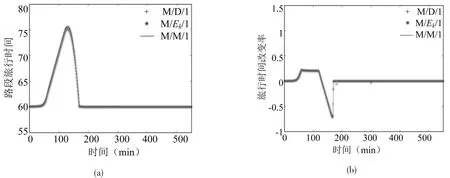
图7 流入率#2下的路段旅行时间及其改变率Fig.7 Link travel time and its change rate under inflow rate#2

在Ran and Boyce[8]及Ban等[4]的研究中可以发现，如果路段交通流动态加载满足先进先出的原则，那么路段旅行时间的改变率总是大于(-1).从图5，图6及图7可以发现，路段旅行时间的改变率在3种不同的流入情况下总是大于(-1)，因此先进先出（FIFO）原则得以满足.

图8 流入率#3下的路段旅行时间及其改变率Fig.8 Link travel time and its change rate under inflow rate#3

5 研究结论

本文基于流体逼近的思想，探讨了路段交通流动态加载中常用的点排队模型，简要回顾了之前研究中提出的基于流体逼近的连续型点排队模型，克服了原有点排队模型中排队出现负值的情况.通过分析可以发现，原有的点排队模型实质上属于具有单一服务台和无限容量的排队模型，基于流体逼近的思想去重新定义了原有的点排队模型.其中3个主要部分是流量守恒模型，车辆流出模型和时间相关的服务台模型，这3个模型全部都是连续的.由于基于流体逼近的连续型点排队模型的计算需求较高，本文采用Backward离散化的方式，提出了离散型的流体逼近模型，并基于此对原有点排队模型进行重新定义.通过模拟可以发现，离散型的流体逼近模型克服了原有点排队模型中出现负排队的情形，并且路段交通流动态加载过程满足先进先出原则.将本文提出的模型应用到动态用户均衡或者动态系统最优的研究中，是接下来的研究方向之一.

[1]VickreyW.Congestiontheoryandtransport investment[J].The American Economic Review,1969, 59(2):251-260.

[2]Nie Y,Ma J,Zhang H.Apolymorphicdynamic network loading model[J].Computer-Aided Civil and Infrastructure Engineering,2008,23(2):86-103.

[3]Nie X,Zhang H.Delay-function-based link models: theirpropertiesandcomputationalissues[J]. Transportation Research Part B:Methodological,2005, 39(8):729-751.

[4]Ban J X,Pang J,Liu H X,et al.Continuous-time point-queue models in dynamic network loading[J]. Transportation Research Part B:Methodological,2012, 46(3):360-380.

[5]Han K,Friesz T L,Yao T.A partial differential equation formulation of Vickrey's bottleneck model, partI:Methodologyandtheoreticalanalysis[J]. Transportation Research Part B:Methodological,2013, 49(5):55-74.

[6]Ji X,Zhang J,Ran B,et al.Fluid Approximation of Point-queue Model[J].Procedia-Social and Behavioral Sciences,2014,138:470-481.

[7]Wang W,Tipper D,Banerjee S.A simple approximation for modeling non-stationary queues[C].Proceedings of the IEEE,Fifteenth Annual Joint Conference of the IEEEComputerSocieties,NetworkingtheNext Generation:Infocom,1996,96(1):255-262.

[8]Ran B,Boyce D E.Modeling dynamic transportation networks:An intelligent transportation systems oriented approach,2nd revised edn[M].Springer-Verlag New York,1996.

Dynamic Link Traffic Flow Loading Based on Fluid Approximation

JI Xiang-feng1，2,ZHANG Jian1，2,RAN Bin1，2
(1.Jiangsu Key Laboratory of Urban ITS,Southeast University,Nanjing 210096,China;2.Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies,Nanjing 210096,China)

Dynamic link traffic flow loading is an essential component in the dynamic traffic assignment.In the loading models,point-queue model is widely used in discrete-time or continuous-time form.Based on the previous work,this paper briefly reviews the continuous time point queue based on the fluid approximation, which overcomes the negativity problem of original queue.Based on the observation that the original pointqueue model is actually a queuing model with a server and infinite buffer,a fluid flow approximation model is proposed to interpret the original point-queue model.Three essential components are a flow balance function,an exit flow function and a time-dependent capacity utilization ratio function,which are all in continuous form.Finally,with the discretization of the proposed model,outflow and queue are simulated on the link in three different scenarios,and the non-negativity of queue and flow first in first out(FIFO)can be easily observed.

traffic engineering;continuous point-queue model;queueing system;fluid approximation; discretization;non-negativity of queue;FIFO

1009-6744（2015）05-0195-07

U1

A

2014-12-08

2015-05-09录用日期：2015-05-25

国家重点基础研究发展计划（973计划）（2012CB725405）；国家自然科学基金（51308115）；东南大学优博基金（YBJJ1344）.

纪翔峰（1986-），男，山东青岛人，博士生. ＊

bran@seu.edu.cn