既定列车作业计划下高铁站可用能力算法研究
陈韬,倪少权*,潘金山,申雪松
(1.西南交通大学a.交通运输与物流学院;b.全国铁路列车运行图编制研发培训中心,成都610031;2.综合交通运输智能化国家地方工程联合实验室,成都610031;3.北京铁路局运输处,北京100860)
既定列车作业计划下高铁站可用能力算法研究
陈韬1,2,倪少权*1,2,潘金山1,2,申雪松3
(1.西南交通大学a.交通运输与物流学院;b.全国铁路列车运行图编制研发培训中心,成都610031;2.综合交通运输智能化国家地方工程联合实验室,成都610031;3.北京铁路局运输处,北京100860)
高铁站可用能力计算对确定列车开行方案的可行性有重要意义.首先分析了高铁站可用能力的影响因素,然后构建了基于股道空闲时段的高铁站可用能力数学模型,提出了先验性优化策略与智能优化算法相结合的双阶段算法对模型求解.其中,第一阶段是综合运用最小股道空闲时段优先、最大平行进路优先、股道空闲时间段内出发时间最小的列车类型优先等策略规则求出模型可行初始解,第二阶段是在初始解基础上运用禁忌搜索算法寻找模型优化满意解,最后用实例对算法的有效性进行验证.
铁路运输;可用能力计算;双层算法;高铁站;列车作业计划
1 引言
我国高铁新线相继开通,高铁联网格局逐渐形成,诸多高铁站衔接线路方向也随之增加.为制定优质列车开行方案,以充分发挥高铁成网优势,需对高铁站可用能力进行计算和评估.目前,在全路编制开行方案及运行图工作中,高铁站可用能力主要还是依靠编图人员的经验及手工调图试凑的方法进行计算,局限性突出,因此有必要对其优化算法进行研究,提高工作效率.
可用能力是指在既定车站作业计划和列车进路排列方案下,车站在某时段内可增加的最大接发列车数,属于一种特殊的通过能力利用场景[1],目前,主要运用计算机模拟法研究该问题,但相关文献不多.文献[1]中提出了求解车站通过能力的列车路径压缩优化模型和加密方法,该方法有利于车站能力利用率的评估.文献[2]~文献[4]运用基于极大代数的petri网、资源树冲突解决等技术,对高铁站通过能力的仿真场景建立及计算进行了相关研究,但对既有列车作业计划场景下的车站通过能力涉及较少.本文在前人基础上,对既有列车作业计划下的高铁站通过能力问题开展分析,提出了运用先验性优化策略与智能优化算法相结合的双阶段算法,并进行了实例验证.
2 问题分析
高铁站可用能力计算的影响因素主要有3方面:
(1)车站固定设备资源及作业组织规则对可用能力的影响.
车站固定设备资源包括:车站到发线、道岔、信号机等及其相互联锁关系;作业组织规则包括:各种作业时间标准、列车安全间隔标准等.这些都是可用能力计算时必须满足的时空资源约束条件.
(2)既定列车作业计划对可用能力的影响.
高铁站可用能力的计算本质上是对车站某时段内剩余时空资源的最大化利用.由于既定列车作业计划的存在,割裂了整个车站的时空资源,车站剩余可用的时空资源呈现碎片化,这些时空资源碎片主要体现为多个股道空闲时段,如图1(a)和图1(b)所示,由于列车的既定计划安排,导致某时段内分别出现了4个和3个股道空闲时段,可用能力被限定其中.因此,高铁站可用能力计算可以转化为求解车站某时段内的所有股道空闲时段内可增加的最大列车数及其作业方案.

图1 股道空闲时段分布图Fig.1 Idle periods of tracks
(3)可用能力计算时新增列车的作业方案对可用能力的影响.
在各种时空资源约束确定的条件下,可用能力计算时新增列车采用的作业方案对可用能力影响较大.列车作业方案包括:
①车流构成类型的确定.
车流构成类型由列车种类(速度、型号)、列车作业性质(站折、出段、入段)及列车到发方向确定,不同的车流构成类型会影响可用能力计算结果不同.以列车到发方向为例,如图2所示(实线线条表示已经安排的列车,虚线线条表示新增列车),在相同的股道空闲时段内,图2(b)中安排的第2个列车是折角列车,发车最小间隔时间不足,致使可安排列车数量比图2(a)中少.本文采用列车出发时间为指标来衡量不同列车类型对资源的占用情况,特定的股道空闲时段中,出发时间越小的列车类型时间资源占用越少.
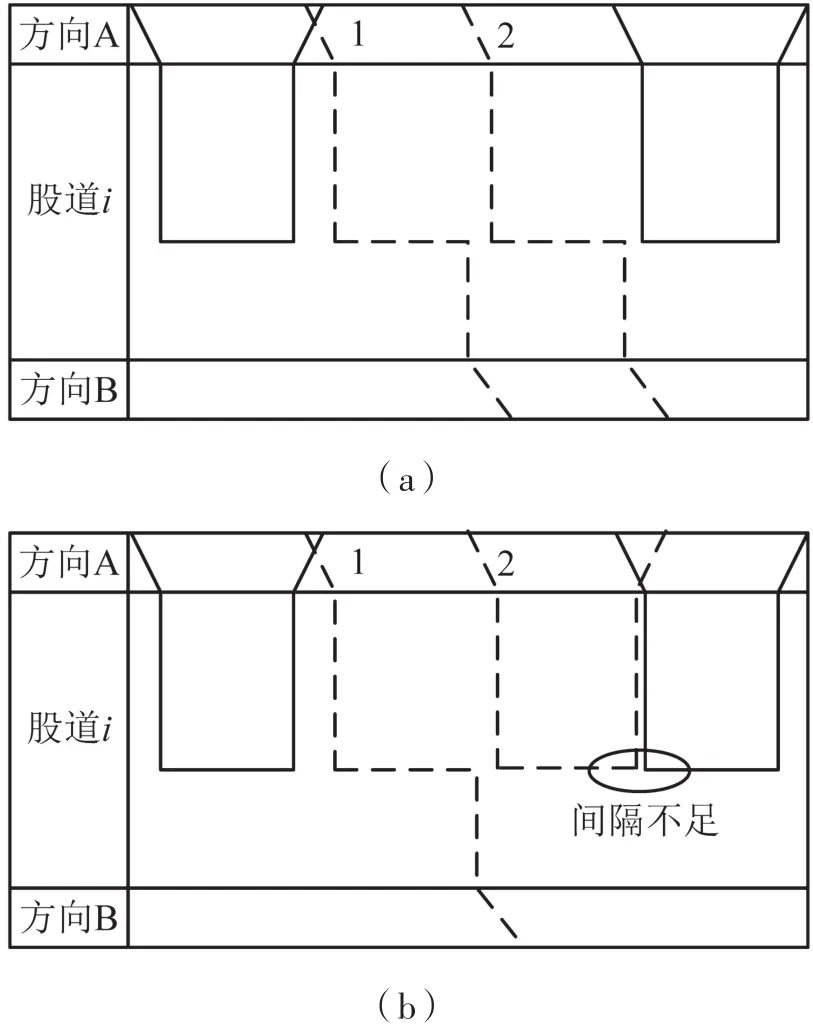
图2 车流构成类型对可用能力的影响Fig.2 The influence on available capacity of various train type
②列车到发时刻的确定.
由图2可知,当列车类型确定后,列车到发时刻主要由股道空闲时段起止时间、各种最小列车车站间隔约束、及列车停站时间几个要素决定.
③列车接发股道及进路的安排.
由于列车股道作业间耦合性极强,同一个列车不同的股道空闲时段选择方案,可用能力计算结果可能会不同,如图3所示(实线线条表示已经安排的列车,虚线线条表示新增列车),当图3(a)中的列车1从股道1调整到股道2后,如图3(b)所示列车2就无法安排了.由于列车接发股道只能在有空闲时段的股道间选择,而且列车到发时刻也取决于股道空闲时段,因此,列车的接发股道安排实际上就是股道空闲时段的安排,每个列车在同一时刻内仅能安排一个股道空闲时段.本文按照生产调度中紧张资源优先原则,采用最小空闲时段股道优先规则、最大平行进路优先规则确定列车股道及进路方案.

图3 列车接发股道及进路安排对可用能力的影响Fig.3 The influence on available capacity of train track and route arrangement
综上所述,高铁站可用能力计算就是在车站资源与既定列车作业计划约束条件下,以列车构成类型、列车股道及进路安排、列车到发时刻为决策变量的,某时段内列车最大新增数.下面对问题进行抽象假设并建立模型,为了缩小模型求解空间,需要确定某时段内的所有股道空闲时段.
3 数学模型
3.1 条件假设及符号说明
某高铁枢纽站有M个衔接方向、S条到发股道;每个衔接方向有Li(i∈M)条接发车进路、P个已安排计划的列车;每个列车是一个七元组的变量分别表示每个列车的到达方向、出发方向、接发股道、接车进路、发车进路、股道占用开始时间、股道占用结束时间;假设高峰小时段的车站可增加列车数为Pnew,求Pnew的最大值.
需要注意,根据现行列车运行图规定,高铁站的列车出入动车所的时刻点必须在运行图上直接确定,因此把动车所视作车站一个衔接方向,从动车所方向接发的车为出入段车,各方向列车股道停留时间为.设新增列车等级、长度、速度、都相同,作业安排时需要满足各种最小车站间隔).高峰时段内不设天窗及非列车作业时间.
3.2 股道空闲时段的确定
3.3 模型建立
给出高铁站可用能力计算模型

约束条件:
股道空闲时段占用唯一性约束如式(3)~式(7).
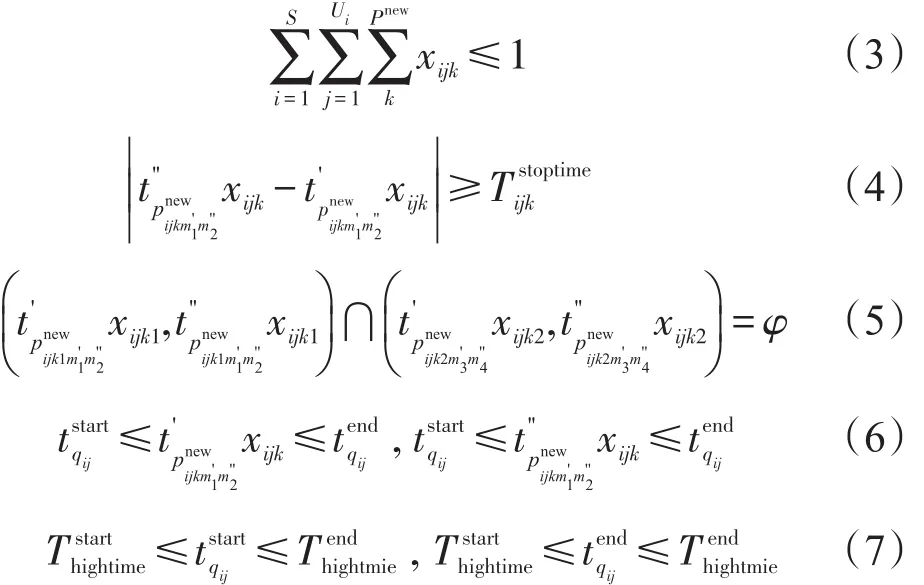
接发进路占用唯一性约束如式(8)~式(17):



式(1)表示新增列车数量最大化;式(2)表示尽量按照股道固定使用方案安排列车.
式(3)表示每个列车仅能安排一个股道空闲时段;式(4)表示每个列车股道占用时间要大于等于规定的股道停留时间标准;式(5)表示每个股道空闲时段内的任何列车占用时间都不能冲突;式(6)表示每个列车的到发时间必须满足股道空闲时段的时间起止约束;式(7)表示每个股道空闲时段的起止时间满足高峰小时段时间起止约束.
式(8)表示每个列车仅能安排一条接车进路及一条发车进路;式(9)~式(12)表示新增列车间的接发车进路设备占用冲突时,要满足车站安全间隔时间标准;式(13)~式(16)表示新增列车与既定作业计划列车的接发车进路设备占用冲突时,要满足车站安全间隔时间标准约束;式(17)表示为列车安排的到发线股道与被安排的接发车进路设备相连通.
式(18)是列车安排股道空闲时段的决策变量;式(19)和式(20)是列车安排接发车进路的决策变量.式(21)和式(22)是模型中其他参数的取值范围.
4 算法设计
4.1 算法思路
高铁车站可用能力计算是一个NP问题[2].为解决该问题,本文采用爬山能力较强且适合离散解空间的禁忌搜索算法进行计算.禁忌搜索算法对初始解有较强的依赖性,因此,本文将分为两个阶段进行求解:
第1阶段,综合运用最小股道空闲时段优先规则(按时段长短对所有股道空闲时段进行排序,时段长度小的股道空闲时段优先增加列车并安排作业)、最大平行进路优先规则[7](对增加的列车安排接发车进路时,优先安排具有最多平行进路的进路)、股道空闲时段内出发时间最小的列车构成类型优先规则(某个股道空闲时段内,每增加一个列车时,该列车类型的确定遵循优先选择接发进路安排后出发时间最小的列车类型),在每个股道空闲时段内增加列车并安排作业计划,得到满足各种时空资源约束的一个初始方案.第1阶段算法仅能保证每个股道空闲时段内列车作业安排的优化性,属于局部优化过程.
第2阶段,运用禁忌搜索算法,以列车数量增加最大化为优化目标,对第1阶段初始方案进行改进,实现全局方案优化,具体方法为:采用2-opt原则交换两个不同股道空闲时段的安排顺序,然后运用股道空闲时段内出发时间最小的列车类型优先规则、最大平行进路优先规则,在调整后的每个股道空闲时段内增加列车并安排作业计划,直到达到算法终止条件.
4.2 算法实现
4.2.1 生成初始方案
(1)初始化车站设备参数:股道、道岔、衔接方向及其联通关系,生成车站接发进路表;初始化车站股道作业时间标准、车站间隔时间标准、能力计算起止时间;生成既定车站作业计划.
(2)根据既定列车作业计划,生成股道空闲时段集合{}qij,并按起止时段长度从小到大排序,详见3.2节.
(3)初始化列车类型集合.算法中生成了两个列车类型集合数组,第一个是根据列车类型比例生成的集合数组用以确定列车类型被安排的范围和顺序,第二个是由第一个集合数组中未被安排的列车类型组成,用以挑选出其中出发时间最小的列车类型.
(4)根据最小股道空闲时段优先规则,依次选择一个股道空闲时段,然后对每个股道空时段运用出发时间最小的列车类型优先规则、最大平行进路优先规则进行增加列车及接发车进路安排操作,直到股道空闲时段集合为空.
具体算法流程如图4所示.
4.2.2 运用禁忌搜索算法寻找高铁车站可用能力优化解[6]
在可用能力初始方案基础上,运用禁忌搜索算法寻找优化解.禁忌搜索算法的关键是要设计合理的邻域结构、评价函数、禁忌表、终止规则.
(1)初始解.
以上一步骤中的新增列车数及排列初始方案为初始解.
(2)邻域结构.
本文中满足2-opt映射的解,即在已排序的股道空闲时段集合中,两个不同的股道空闲时段交换顺序后产生一个邻域解,则领域规模为
(3)评价函数.
以新增列车数为评价指标,数值越大则方案越好.
(4)候选解集.
邻域解中选取股道空闲时间段数的平方根为候选集范围,即候选解集大小为,将候选解集中新增列车数最大的方案作为新的当前解进行下一次迭代搜索.
(5)禁忌表.
将已经评价过的股道空闲时段排列方案及其评价值进行禁忌,贮存在禁忌表内,本文的禁忌表用链表结构来表示.为了获得较好的搜索效果,采用动态禁忌长度.本文根据频率信息动态控制禁忌的长度,当一个目标函数值重复出现,可以增加禁忌长度以避开循环.
(6)特赦条件.
为了避免丢失最优解,规定在找不到领域解及迭代一定次数后,特赦禁忌表中最优值为当前解继续进行迭代搜索.
(7)终止条件.
设置最大迭代次数作为终止条件.
(8)算法流程.
①设迭代次数为1,将可用能力计算初始方案置为当前方案;
②随机对换2个不同的股道空闲时段后,并按照第一阶段中算法流程,进行新增列车及作业安排,生成邻域解,以最大评价指标对邻域解进行评价;
③判断邻域解中对象是否满足藐视准则,选择邻域解中未被禁忌的对象及满足藐视准则的禁忌对象为候选解,更新禁忌表;
④迭代次数增加1,若迭代次数为最大迭代次数或者最大值出现频率较高时,算法终止,输出最优方案,否则转②.
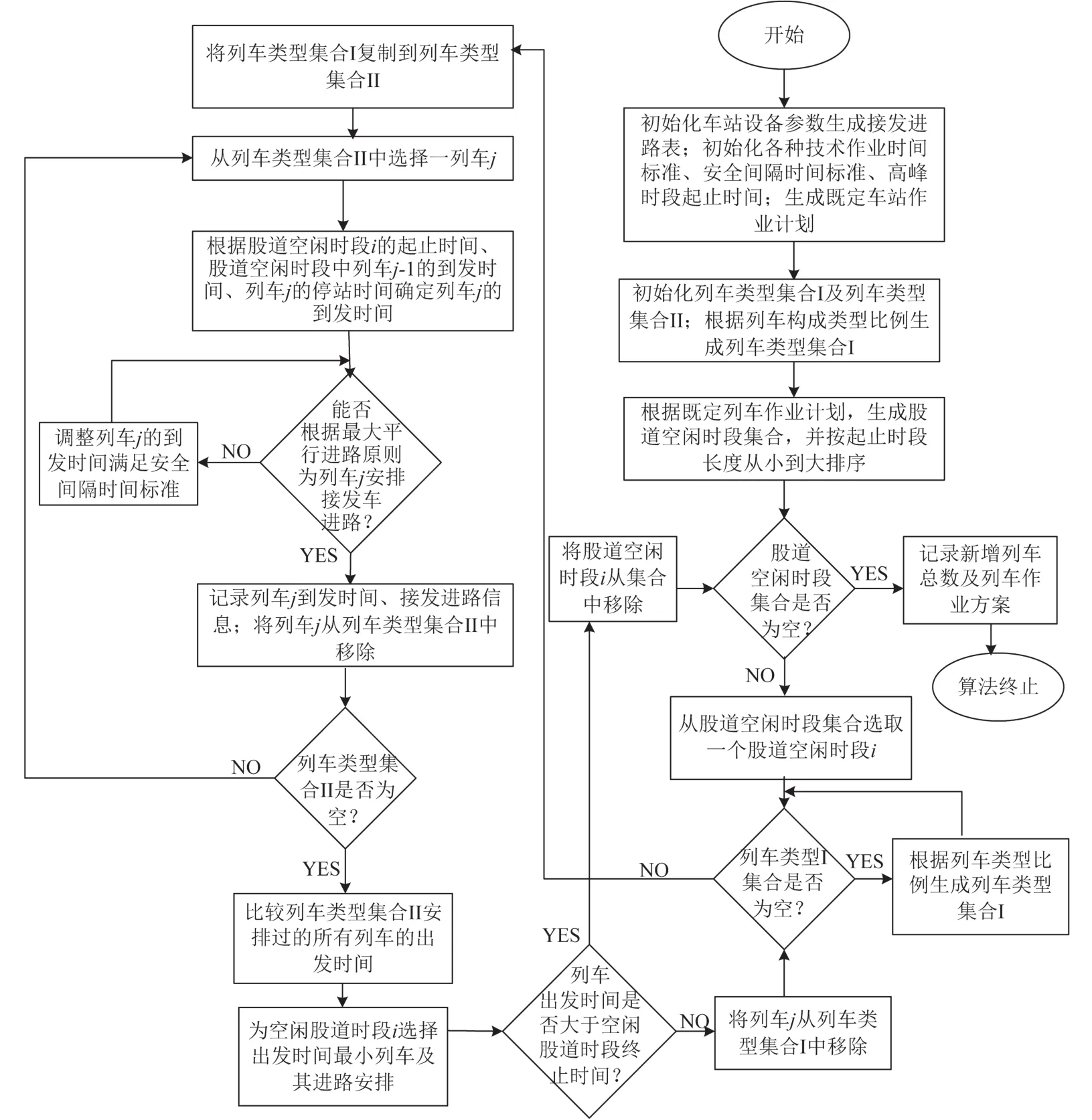
图4 第一阶段算法流程Fig.4 The first-stage algorithm flow
5 算例
以某真实大型高速铁路枢纽站为例对算法的有效性进行验证.该车站共有3个衔接方向,其中C为动车所方向,各方向间都有列车到发,站场图如图5所示.列车到达追踪间隔3 min、列车出发追踪间隔3 min、列车不同时发到间隔时间8 min、列车不同时到发间隔时间2 min,车站不考虑延续进路,列车不能在正线停车,列车停留时间均为6 min,列车在股道上的停留效益相同.车站已安排的列车到发作业计划如图7所示,其中黑框中为高峰时段14:00-17:00的作业计划共16列车,求此情况下14:00-17:00内的可用能力.

图5 高铁站站场图Fig.5 HSP station yard diagram
运用本文算法进行高铁站可用能力计算,首先得到14:00-17:00的股道空闲时段共26段并从小到大排序,运用第一阶段算法得到初始方案,然后运用第二阶段禁忌搜索算法寻求优化解,当迭代次数为60次后,得到图6所示结果,最大增加列车数为39列,其作业计划的时空分布如图8所示.运用文献[1]中的压缩加密法计算本算例的高峰时段可用能力,首先压缩既有计划16列车间的缓冲时间,然后加密5次后,最终得到可用能力结果为36列,比本文算法计算结果少3列,主要原因是压缩已安排计划的列车作业缓冲时间会破环股道空闲时段时空分布,导致可用能力的计算结果失真,由此也表明了本算法的可行性和优化性.

图6 可用能力计算优化迭代过程Fig.6 The iterative process of optimization

图7 给定车站作业计划图Fig.7 Train reception and departure plan diagram
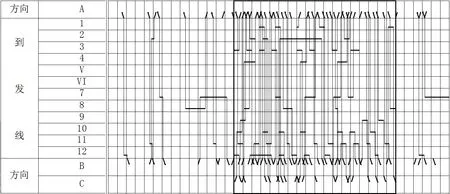
图8 高峰时段可用能力计算后车站作业计划图Fig.8 Train reception and departure plan diagram after available capacity calculation
6 研究结论
既定列车作业计划下的高铁站可用能力计算问题属于典型的NP问题,运用计算机模拟法求解效率较高.本文提出了基于股道空闲时段的先验性优化策略与智能优化算法相结合的双阶段算法,为该问题的解决提供了一个有效的思路.
[1]刘敏,韩宝明,李得伟,等.高速铁路车站通过能力计算和评估[J].铁道学报,2012,34(4):9-15.[LIU M, HAN B M,LIU H D,et al.Calculation and evaluation of carrying capacities at high-speed railway stations[J]. Journal of Railway Society,2012,34(4):9-15.]
[2]Peter S.Calculation of realistic railway station capacity by plat forming feasibility checks[C].2nd International Conference on Models and Technologies for Intelligent Transportation Systems,2011.
[3]张嘉敏.基于双层模型的高速铁路车站能力计算与评估[J].交通运输工程与信息学报,2014,4:39-48 [ZHANG J M.Calculation and evaluation of station capacity for high speed railway based on bi-level model[J].Journal of Transportation Engineering and Information,2014,4:39-48.]
[4]钟俊,王正彬,等.客专车站高峰通过能力一体化计算研究[J].交通运输工程与信息学报,2012,2:125-131.[ZHONG J,WANG Z B,et al.Study on integrated algorithm for the peak through capacity of a dedicated passenger line terminal[J].Journal of Transportation Engineering and Information,2012,2:125-131.]
[5]史峰,谢楚农,于桂芳,等.铁路车站咽喉区进路排列优化方法[J].铁道学报,2004,26(4):5-9.[SHI F,XIE C N,YU G F,et al.Optimization methods for arranging train routes in station bottleneck[J].Journal of Railway Society,2004,26(4):5-9.]
[6]王凌.智能优化算法及其应用[M].北京:清华大学出版社,2004.[WANGL.Intelligentoptimization algorithm and its application[M].Beijing:Tsinghua Univercity Press,2004.]
HSR Passenger Station Available Capacity Calculation under Train Reception and Departure Plan Established
CHEN Tao1,2,NI Shao-quan1,2,PAN Jin-shan1,2,SHEN Xue-song3
(1a.School of Transportation and Logistics;1b.National Railway Train Diagram Research and Training Center,Southwest Jiaotong University,Chengdu 610031,China;2.National United Engineering Laboratory of Integrated and Intelligent Transportation,Chengdu 610031,China;3.Beijing Railway Bureau Transportation Department,Beijing 100860,China)
The calculation of HSR passenger station available capacity is of great significance to determine the feasibility of passenger train operation plan.The main influence factors of HSR available capacity firstly are analyzed.Then mathematical model of HSR available capacity based on the idle periods of tracks is built. A two-level heuristic algorithm,in which some optimization strategies are combined with intelligent optimization algorithm,is offered.In the first level,a feasible initial solution is found by using the policy of minimum idle period of track priority,the maximum parallel route priority,the minimum departure time of train type priority.In the second level,the Tabu search algorithm is used to search a satisfied solution based on the initial solution.At last,an example is used to validate the effectiveness of the proposed algorithm.
railway transportation;calculation of available capacity;two-level algorithm;high-speed passenger station;train reception and departure plan
1009-6744(2015)05-0178-08
U268.6
A
2015-05-13
2015-07-08录用日期:2015-07-21
国家自然科学基金(61273242,61403317,60776826);四川省科技厅软科学计划项目(2015ZR0141);中央高校基本科研业务费专项资金资助(2682015CX043);中国铁路总公司科技研究计划项目(2015X008-B,2014X004-D).
陈韬(1981-),女,广西柳州人,博士生. *
shaoquanni@163.com

