加权复合算子的新刻画
郭新翠
(天津大学理学院,天津300072)
记D为复平面C中的单位圆盘H(D)和S(D)分别表示D上的全纯函数和全纯自映射的全体.任意的 f∈H(D),若)|f'(z)| <∞,则f属于Bloch空间.若定义范数‖f‖B=|f(0)|+βf,则 Bloch空间是不变的 Banach空间.Bloch空间上的函数f满足:
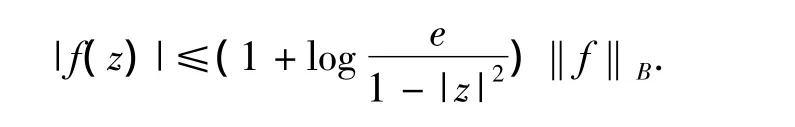
另一类我们常见的Möbius不变空间是解析Besov空间(1<p<∞),用Bp表示

其中dA表示单位圆盘的标准化面积测度.而在这里bp是一个半范数,并且可以验证Besov空间在定义Besov范数‖f‖Bp=|f(0)|+bp(f)的意义下是Banach空间.对任意f∈Bp,由文献[1]中的定理9和文献[2]中的引理可知,对任意z∈D,有‖f‖Bp,记 Zygmu`nd 空间为 Z,有
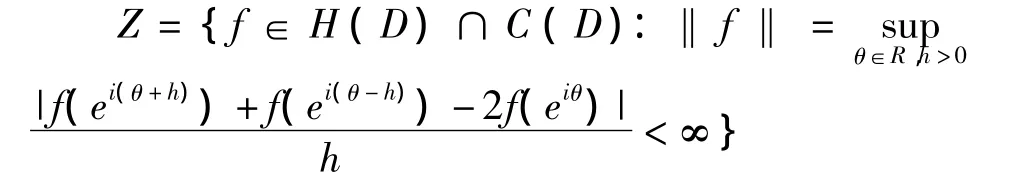
众所周知,f∈Z当且仅当f'∈B,且Z在定义下列范数意义下是Banach空间
对任意的 φ∈S(D),u∈H(D),f∈H(D),z∈D,加权复合算子定义为
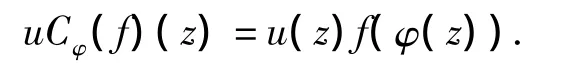
特殊的,当u=1和Cφ=I时,其为复合算子Cφ和乘积算子Mu,即
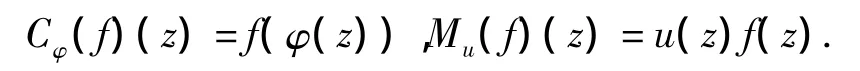
近几十年来函数空间上的复合算子理论[3-5]研究发展是很迅速的.就加权复合算子来说,不仅出现很多单位圆盘上的刻画,还有多圆柱和单位球上的刻画[6].研究的算子性质也是各不相同,包括有界性和紧性[7-9]、本性范数[10]、等距同构[11]等,本文研究的是复合算子有界性和紧性.当然由加权复合算子,可以直接得到乘积算子和复合算子的对应性质,这一点不再特别说明.本文主要受到文献[8]的启发,在文献[8]的定理1和定理3证明过程中,F·Colonna和S·Li应用了文献[7]中的定理1作为引理2,而文献[3]中定理6和定理7是应用文献[7]中的定理2作为引理5.但注意到文献[8]中的引理2和引理5与文献[7]中的定理1和定理2有所差别,并且在文献[8]中定理1证明过程中出现一些计算错误,从而导致其结论的等价性推倒不能严密成立,因此导致后面结论也出现类似的问题.在与F·Colonna通信之后确认存在偏差,针对这些问题,下面通过修改引理和相关检验函数给出了合理的等价性说明.
在有界性部分,定理1和定理2用‖uφk‖Z刻画了Bloch空间和Besov空间到Zygmund空间加权复合算子的有界性并给出等价条件;在紧性部分,定理3和定理4用‖uφk‖Z刻画了Bloch空间和Besov空间到Zygmund空间加权复合算子的紧性,并给出等价条件.另外注意到 Bloch空间和Besov空间的情况是一致的,即{hp,a}(p=∞)很适合刻画Bloch空间到Zygmund空间加权复合算子的有界性和紧性,而这是文献[8]所否定的.
1 有界性
为了刻画Bloch空间和Besov空间到Zygmund空间加权复合算子的有界性,我们先给出引理1.固定 a∈D 和 z∈D,取和.容易验证它们都属于Bloch空间.
引理1[7]若u∈Z且 φ∈S(D),则下列条件是等价的.
(a)这里pk(z)=zk,k为非负整数.
(b)N1∶uCφfφ(w),j‖Z,j=1,2,3 都有界.
(c)M3∶和M2有界.
定理1 若u∈Z且φ∈S(D),则下列条件是等价的.
(a)加权复合算子uCφ∶B→Z有界.
(c)Ni,i=1,2 和 Aj,j=1,2,3 以及 H 都有界.
(d)M1,M2和 M3有界,其中 M1=szupD(1-|z∈
证明:因为此定理应用引理1,并且证明大部分与文献[8]中的定理1类似,这里只证由(c)推得(d).
若 Ni,i=1,2 和 Aj,j=1,2,3 以及 H 有界,由引理1,M2和M3有界,下面仅需要证明M1有界.对任意正整数n>0和a∈D,由直接的计算可知
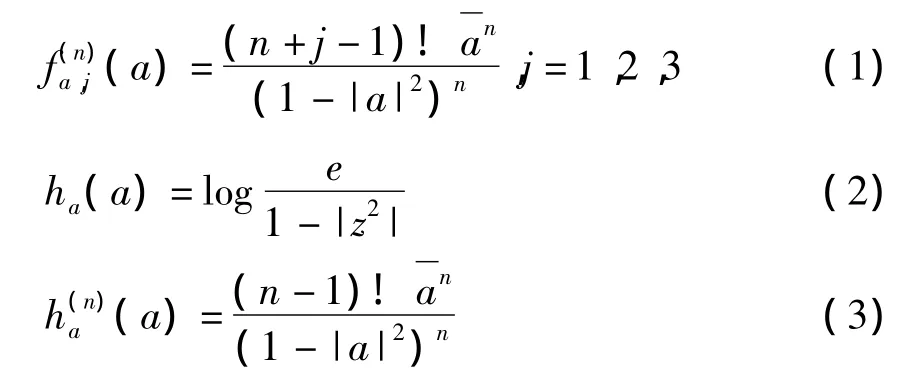
因此,由式(1)~(3)计算可以得到

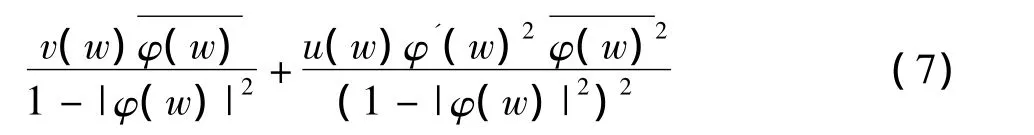
于是由式(4)~(7)得到
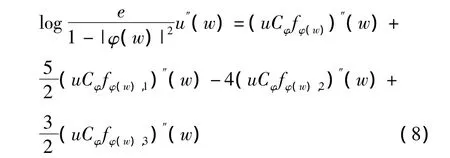
对式(8)左右两侧乘(1-|w|2)并取模得到
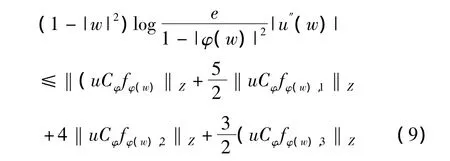
在式(9)中对w∈D取上确界,即得M1有界.
下面的定理刻画了Besov空间Bp(1<p<∞)到Zygmund空间加权复合算子的有界性,这与文献[8]中定理3的等价结论也不同.由于证明基本一致,这里省略具体过程.对固定的a∈D和z∈D,定义,容易验证 hp,a(z)∈Bp.
定理2 若u∈Z,φ∈S(D),对1<p<∞,则下列条件等价.
(a)加权复合算子uCφ∶Bp→Z有界.
(b)且 Hp∶,其中pk(z)=zk,k为非负整数.
(c)定理 1.2 中的 Ni,i=1,2 和 Aj,j=1,2,3有界,且有Hp界.
(d)M4,M2和M3都有界,其中M4=szupD(1-|∈
2 紧性
为了刻画Bloch空间和Besov空间到Zygmund空间加权复合算子的紧性,我们先给引理,再给定理,其中的引理3代替文献[8]中的引理5.
在下面定理3证明中,用到引理2和3以及公式(7),这是与文献[8]所不同的,但是证明思路与文献[8]中定理6基本一致,故省略.
定理4给出Besov空间到Zygmund空间加权复合算子的紧性的等价刻画,由于与定理3相似的理由,省略具体的证明过程.
引理2 若 u∈H(D),φ∈S(D),1<p<∞,则加权复合算子 uCφ∶B→Z(或者 uCφ∶Bp→Z)紧的充分必要条件是uCφ∶B→Z(或者uCφ∶Bp→Z)有界且B(或者Bp)上在单位圆盘D的紧子集上一致收敛于0的有界序列{fk},当k→∞时,有‖uCφfk‖Z→0.
引理3[7]若 u∈Z,φ∈S(D),则下列条件等价.
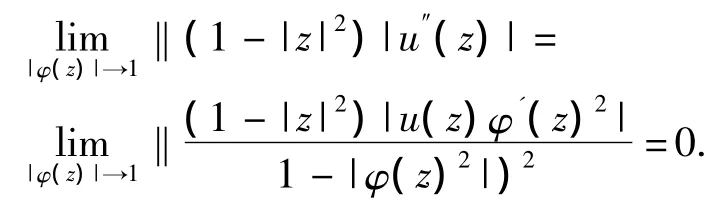
定理3若u∈Z,φ∈S(D)并且 uCφ∶B→Z设有界,则下列条件等价.
(a)加权复合算子uCφ∶B→Z是紧的.
其中 pk(z)=zk,k 为非负整数.

(c)‖Z=0,其中 j=1,2,3.
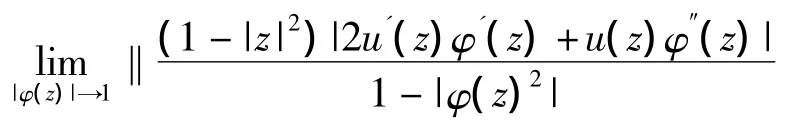
(d)=0,且
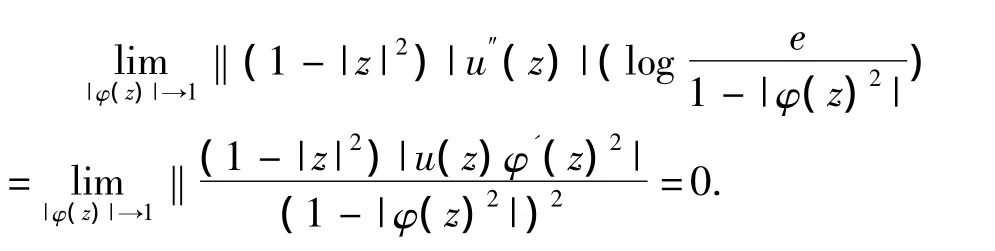
定理4 若u∈Z,φ∈S(D),1<p<∞ 假设加权复合算子uCφ∶Bp→Z有界,则下列条件是等价的.
(a)加权复合算子uCφ∶Bp→Z是紧的.
且
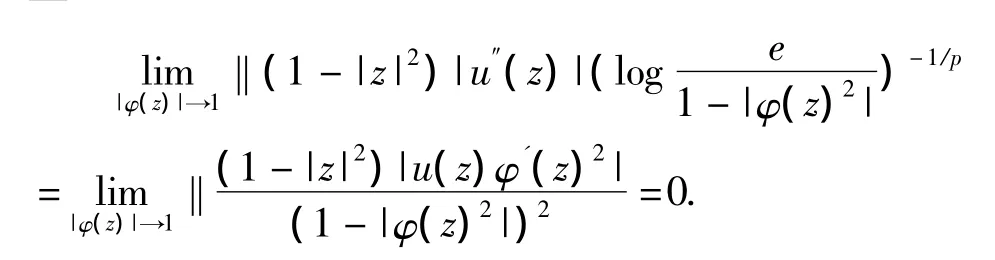
3 结语
本文纠正了原有文献的多处错误,其中不仅包括两次引用的错误,还包含定理叙述错误和证明计算推理多次.总结出下面两个可以由定理1~4直接得到的推论,这也证明了文献[8]中的一处错误表述.
推论1 若 u∈Z,φ∈S(D),对1<p≤∞,则下列条件等价.
(a)且Hp∶
(b)Ni,i=1,2 和 Aj,j=1,2,3 有界,且 Hp有界.
(c)M4,M2和 M3有界,其中 M4=supz∈D(1-
推论2 若 u∈Z,φ∈S(D),1 <p≤∞,则下列条件等价.

[1]ZHU K H.Analytic Besov spaces[J].Journal of Mathematical Analysis and Applications.1991,157(2):318-336.
[2]TJANI M.Compact composition operators on some Möbius invariant Banach spaces[D].Michigan:Michigan State University,1996.
[3]COWEN C C,MACCLUER B D.Composition operators on spaces of analytic functions[M].Boca Raton:CRC Press,1995.
[4]ZHU K H.Operator Theory on Function Spaces[M].New York:Marcel Dekker,1990.
[5]SHAPIRO J H.Composition Operators and Classical Function Theory[M].Springer-Verlag,1993.
[6]STEVIC S,CHEN R Y,ZHOU Z H.Weighted composition operators between Bloch-type spaces in the polydisc[J].Sbornik:Mathematics,2010,201(2):289-319.
[7]COLONNA F,LI S.Weighted composition operators frominto the Zygmund spaces[J].Complex Analysis and Operator Theory,2012,7(5):1495-1512.
[8]COLONNA F,LI S.Weighted Composition Operators from the Bloch Space and the Analytic Besov Spaces into the Zygmund Space[J].Journal of Operators,2013,doi:10.1155/2013/154029.
[9]COLONNA F,LI S.Weighted composition operators from the minimal Möbius invariant space into the bloch space[J].Mediterranean Journal of Mathematics,2013,10(1):395-409.
[10]ZHAO R.Essential norms of composition operators between Bloch type spaces[J].Proc.American Mathematical Society,2012,138(7):2537-2546.
[11]HYVARINEN O,LINDSTROM M,NIEMINEN I,et al.Spectra of weighted composition operators with automorphic symbols[J].Journal of Functional Analysis,2013,265(8):1749-1777.

