混沌时间序列在股票价格长期预测中的应用

顾秋宇，朱 捷，徐 晶

(黑龙江科技大学，哈尔滨150000)

混沌时间序列是一种从无序和复杂的环境中产生出有序和规律的系统，该序列的研究构成混沌理论的重要组成部分.在股票市场上，股票价格时间序列具有多种不确定性和非线性，具备混沌特性.利用混沌时间序列对股票价格进行预测已成为学术界研究的热点.

数学家Vladimir N·Vapnik等通过30余年的严格的数学理论研究，提出来的支持向量机(support vector machine，简称SVM)算法已得到国际数据挖掘学术界的重视，并在语音识别、文字识别、药物设计、组合化学、时间序列预测等研究领域得到成功应用，该新方法从严格的数学理论出发，论证和实现了在小样本情况下能最大限度地提高预报可靠性的方法，其研究成果令人鼓舞.张学工、杨杰等率先将有关研究成果引入国内计算机学界，并开展了SVM算法及其应用研究，但混沌序列的股票市场领域内尚未见SVM的应用报道[1－3].

由于混沌时间序列对初值敏感，预测误差将会迅速放大，如果直接输入SVM算法中，会降低算法的预测效果.本文利用混沌动力系统的相空间延迟坐标重构理论，求出嵌入维数和延迟时间，将SVM算法的核函数进行改进，以减少累积误差，建立混沌时间序列的支持向量机预测模型.实验结果表明，对股票价格的预测，改进的支持向量机模型比RBF模型具有更好的预测效果.

1 混沌时间序列空间重构

一个混沌时间序列的行为由许多有序行为组合而成，所以混沌时间序列预测的基础是状态空间的重构理论，通过相空间重构，可以揭示混沌时间序列的内部结构.

混沌时间序列的数值是通过系统中其他变量相互作用得到的，利用其确定的延迟时间作为系统新的不同坐标上的数值，得到一个多维状态空间，即重构一个与原系统等价的相空间.这个维数通常被称为空间的嵌入维数m，确定的时间延时被称为空间的延迟时间τ.

1.1 延迟时间τ的选取方法

延迟时间是一个重要的相空间重构参数.最佳延迟时间τ不能选的太大也不能太小，当τ选择的太小时，延迟矢量各坐标值之间有很强的相关性，信息不易显露，产生冗余误差;而当τ选择的太大时，重构矢量各坐标值之间的关系几乎变成随机的，破坏了原系统各变量之间的内在关系，将使得重构矢量包含的原动力系统信号失真.因此应该选取合适的τ，使重构矢量保持原动力系统各变量之间的关系.

延迟时间τ与嵌入维数m的选取互不相关，即τ与m的选取是独立进行的.方法主要有:自相关法、复自相关法、去偏自相关法、互信息法和AD法，本文采用了互信息法进行选取.

1.2 嵌入维数m的选取方法

Cao方法是1992年Cao在虚假邻域算法的基础上提出的一种直观、简洁的判定时间序列数据具有非线性和混沌特性的方法[4－6].

对时间序列 x(t1)，x(t2)，…x(ti)，…，x(tn)，重构m维和m+1维相空间，计算:

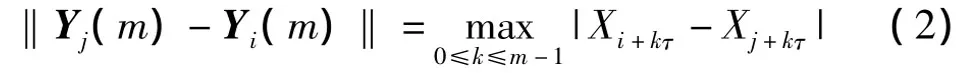
当m＞m0时，E1(m)的值停止变化，得到最小的嵌入维数m0+1.

1.3 Lyapunov 指数

混沌系统的基本特征是系统对初值的极端敏感性，两个几乎相同的初始轨迹随时间产生的分离指数、Lyapunov指数的定量描述这一现象.Lyapunov指数的定义是:取映射F所代表系统在各次迭代点处导数绝对值的对数平均值相空间中的每一维都有其各自的Lyapunov指数是指相空间中邻近轨道发散或收敛的平均指数率.要判断系统是否存在混沌现象，其中一种方法可以从最大Lyapunov指数是否大于零判断:系统中存在一个正的Lyapunov指数，就意味着在这个系统相空间中，无论初始两条轨线的间距多么小，其差别会随着时间的演化，增加发展指数率，达到不可预测，这就是混沌现象.

计算Lyapunov的方法有很多种，通常，在实际运用识别中，只计算系统的最大Lyapunov指数便可，主要的方法有:定义法、Wolf法，Jacobian法，小数据量法等等.

本文通过Wolf法计算Lyapunov指数.易知，当最大λ＞0时，系统存在混沌特性.

2 改进的最小支持向量机算法

分析长期累积误差，找到减小误差的条件.在预测过程中应用最小二乘支持向量机，为减小累计误差对其中的核函数进行改进，使其改进核函数满足减小误差的条件.用改进的模型进行预测.

2.1 长期预测的累积误差分析

混沌时间序列是具有确定结构的非线性动力学系统，因为混沌时间序列对初值敏感，预测误差将会迅速放大，所以需要对长期累积误差进行分析，找到减小误差的条件.因此在实际应用中，必须考虑折衷的方案—在不改变优化准则的情况下，尽量降低误差累积的速度.长期预测的误差由模型的系数、基函数的导数或偏导数和一步预测误差构成.从误差累积的公式看，其加权系数由训练过程决定，只有基函数可以人为选择.基函数的导数是影响误差累积速度的另一个重要因素.因此，用导数较小的函数作为基函数，误差发散的速度将低于导数较大的函数，这样应用改进的基函数在预测时就能够延长预测时间.因此，改进的基函数应该满足以下两个条件[7－8]:

1)在定义域内具有较小的导函数，即|f'(x)|＜1;

2)具有紧支撑结构，即在定义域外有快速的衰减.

2.2 改进最小二乘支持向量机模型

为了提高支持向量机的计算速度，根据最小二乘法的这些优点，Suykens等人提出了最小二乘支持向量机(LS－SVM)，它是SVM采用二次损失函数的一种形式.最小二乘支持向量机通过非线性映射到高维特征空间中的数据拟合成超平面，同时进行分类，运用最小二乘法求出最优解，提炼出数据包含的信息，它简化了计算量，加快了计算速度.

其他思路与支持向量机相同，通过使用特征映射将线性不可分的样本集映射到高维特征空间中，使它们在高维特征空间是线性可分的.但是在数值计算上，这种思路也存在着一定的问题，这是因为特征空间的维数一般很高，甚至是无穷大，在计算的过程中不容易实现.所以这里SVM将样本空间的内积替换成了核函数，甚至不需要知道映射的形式，只需要知道核函数的形式和基本用法.也就是说，运算实际上是在样本空间进行的，这就是核技巧的思想.选择满足Mercer条件的不同内积核函数，就构造了不同的SVM，这样也就形成了不同的算法.利用SVM根据构建的混沌时间序列输入向量和输出向量进行训练，获取混沌时间序列SVM模型的参数.预测模型的参数所蕴藏的关系就是混沌时间序列的各个向量过去的和将来的关系.至此基于SVM的预测模型已经建立.这样就可以利用该模型预测将来的混沌时间序列的输出[9－10].

基于RBF核函数预测相对精确，为了减小误差，在原来核函数的基础上满足以上减小误差的两个条件及Mercer条件，我们改进核函数模型为:

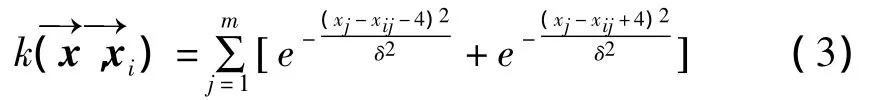
3 股票价格仿真预测

3.1 支持向量机混沌时间序列预测模型

对混沌时间序列重构相空间后，得到支持向量机的一步预测模型为:

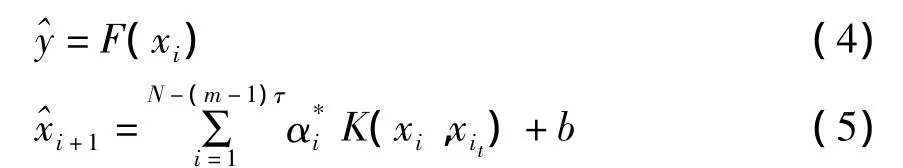
其中 xi1=(xt，…，x(t－(m －1)τ)).

对于相空间的第t+1点预测xit+1=(~xi+1，…x(t－(m －2)τ)).第t+2点预测为:

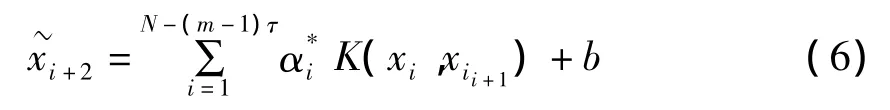
同理我们可以得到第t+p点预测为:

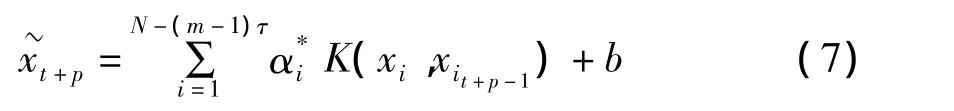
3.2 仿真预测

本文根据2013.11.6 ～2013.12.17 沪市宝钢股份收盘价格得到，最大Lyapunov指数为0.032 5，最大Lyapunov指数大于0，可以断定该股票收盘价是一个混沌系统.依此数据根据图1流程图进行仿真实验.

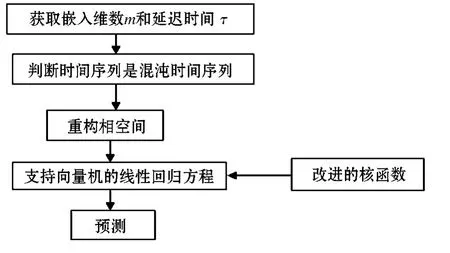
图1 流程图

由互信息法得到图2，第一次达到最小值作为相空间重构的时间延迟τ，即τ=1.由图3 Cao方法计算混沌时间的嵌入维数可以看出，m=3时值停止变化，得到最小的嵌入维数，即m=4.

通过Matlab软件对其仿真，前30个数据用改进的最小二乘支持向量机模型预测后30个数据，将一步预测值补充进时间序列里，去除原始数据中的第1组数据构成新的时间序列，用一步预测下一组30个数据.

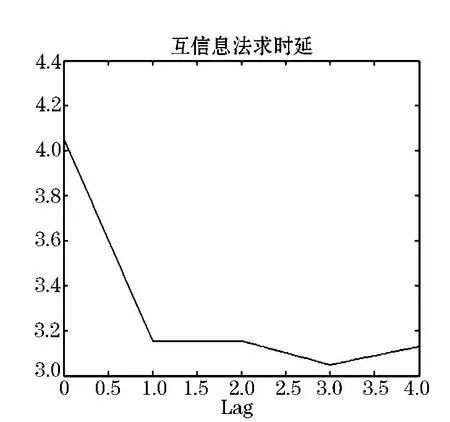
图2 互信息法确定延迟时间

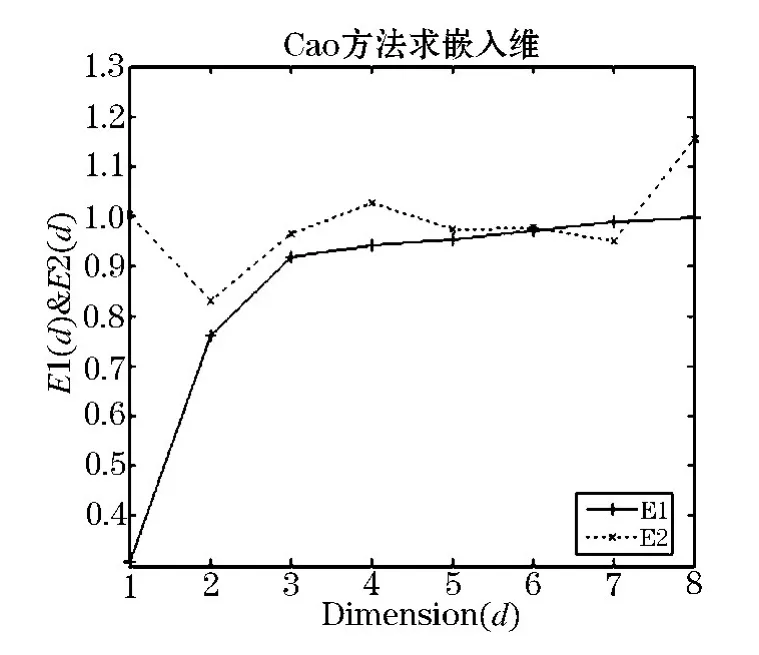
图3 Cao方法确定嵌入维数(m)

股票收盘价格在支持向量机仿真实例中，为衡量预测模型的精确，采用相对误差，评价模型的每一个时间序列的预测效果.

从表1中更清晰看出新核函数的SVM模型预测方法预测的数据相对误差小一些，从第28个数据之后新模型预测更加精确，说明混沌时间序列的股票数据在这种复杂非线性建模中更具有独特的优越性.最后对比径向基核函数(RBF)和改进的核函数模型的预测效果，讨论模型的MSE.其径向基函数(RBF)预测模型的MSE等于24.090 2，新核函数的预测模型的MSE等于21.720 33，可以看出新模型的预测效果更好.

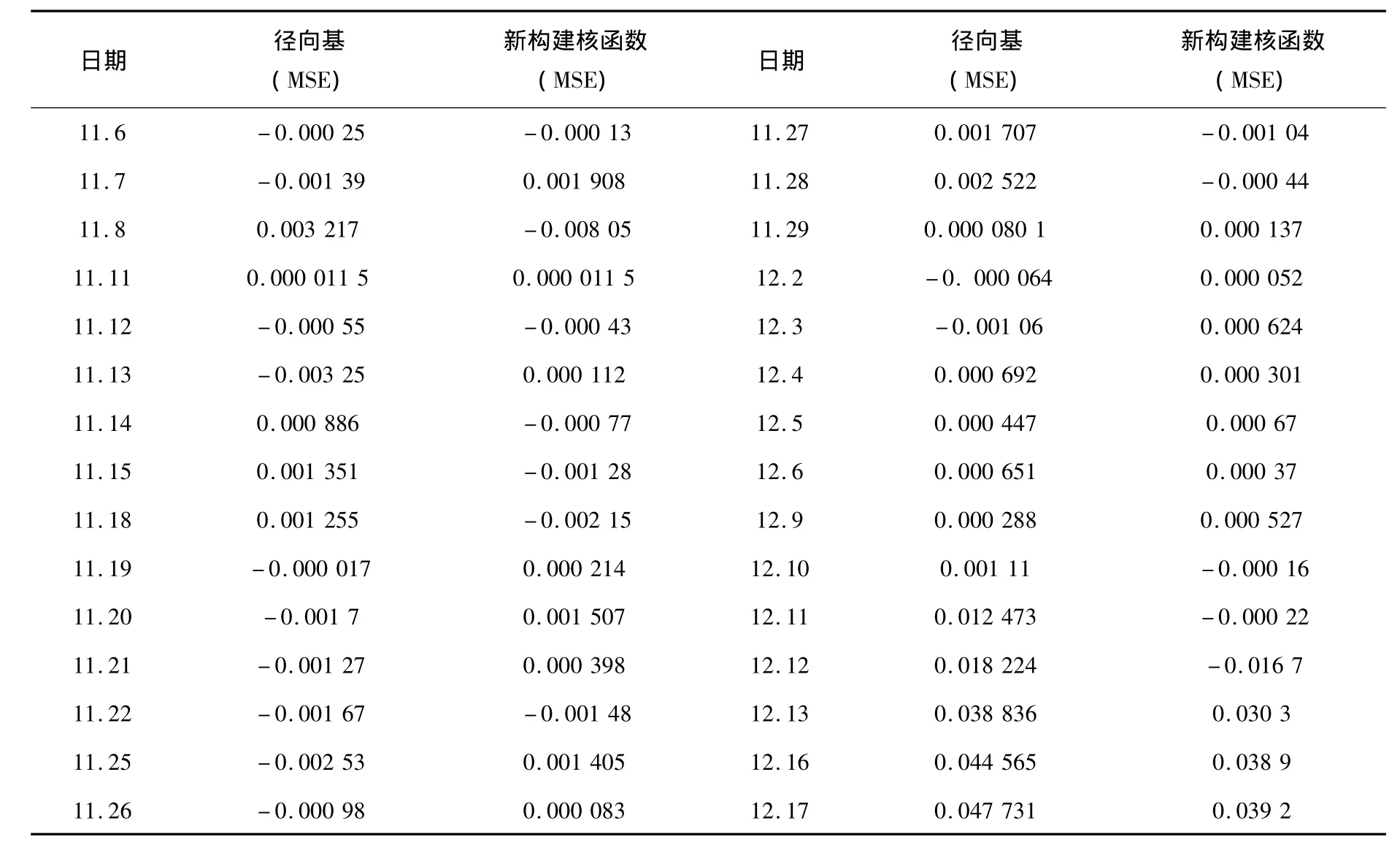
表1 径向基函数(RBF)和改进的核函数预测的对比的相对误差分布图

4 结语

本文的核心内容是结合混沌时间序列的初始敏感性理论，对支持向量机的核函数进行改进，减小长期预测中的累积误差，建立改进的预测模型.并利用股票价格的数据对建立的模型进行训练，SVM模型所蕴涵的函数映射关系就是混沌时间序列中向量的内在关系，应用模型预测未来的股票价格.结果表明:改进的模型更精确，并且在股票价格的长期预测研究中具有很强的实用价值.

[1]吕金虎，陆君安，陈士华，等.混沌时间序列分析及其应用[M].武汉:武汉大学出版社，2001.

[2]梁景波.混沌时间序列的一种长期预测模型研究[D].鞍山:辽宁科技大学，2011.

[3]张淑清，贾 健，高 敏，等.混沌时间序列重构相空间参数选取研究[J].物理学报，2010，5(3):1576－1582.

[4]李春兴，白建东.基于组合预测模型的股票预测方法的研究[J].青岛理工大学学报，2008，29(2):82－85.

[5]陆振波，蔡志明，姜可宇.基于稀疏Volterra滤波器混沌时间序列自适应预测系统工程与电子技术[J].武汉:海军工程大学，2007，29(9):1428－1431.

[6]ZHANG C H，TIAN Y J，ZHANG X F.An Improvement to the Theoretical Foundation of Support Vector[J].Classification or Transactions，2004，8(2):66－71.

[7]SCHOLKONF J，PLATT J，SHAWE － TAYLOR A J，et al.Estimating the support of a high－dimensional distribution[J].Neural Computation，2001，13:1443－1471.

[8]QING F M，YU P H.A new local linear prediction model for chaotic time series[J].Phys Lett A，2007，370(5－6):465－470.

[9]杨博文，马敬慧.基于混沌理论视角的国际油价波动复杂性分析[J].西南石油大学学报，2010(5):1－6.

[10]许 楠，刘丽杰，徐耀群.高斯激励混沌神经元系统及其应用[J].哈尔滨商业大学学报:自然科学版，2014，30(5):599－603.