运用多种图表延展，提高数据统计能力

张昀

在新课程标准的指引下，数学教学方法也在不断改进、创新。数学教学不应局限于一个狭窄的课本知识领域里，应该是让学生对知识和技能初步理解与掌握后，进一步的深化和熟练，使学生在学习中学会运用课本的知识举一反三，达到“温故而知新”，提高综合运用知识解决问题的能力。

原题：（苏科版教材八上第25页）

某校为了解八年级学生身高的范围和整体分布情况，抽样调查了八年级50名学生的身高，结果如下（单位：cm）

怎样描述这50名学生身高的分布情况？

解：（1）计算最大值与最小值的差

在这组数据中，最大值是172cm，最小值是147cm，它们的差是25cm.

（2）决定组距与组数

如果取组距为3cm，由于 =8 ，组数适当，所以可将这组数据分为9组.

（3）列频数分布表 （4）画频数分布直方图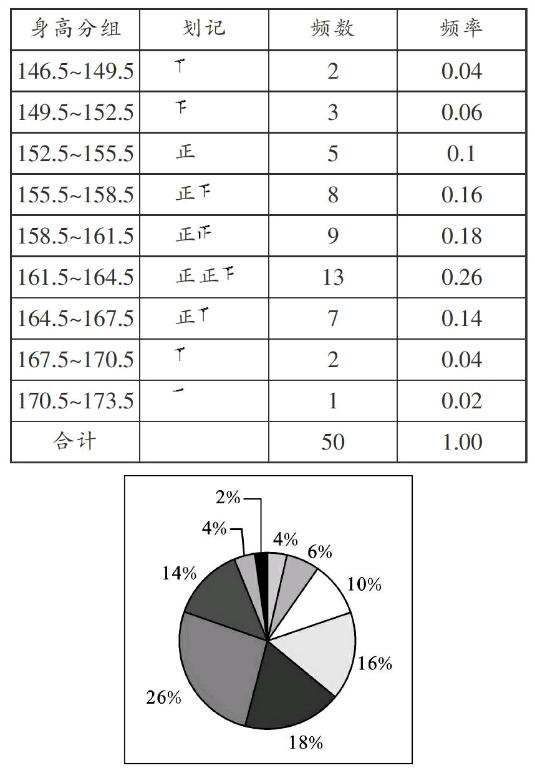

透析：（1）解题步骤：计算最大值与最小值的差，确定统计范围；决定组数与组距，数据越多，分组应越多，当数据在100个以内时，通常按照数据的多少分成5～12组；确定分点，通常为了使得每个数据都落在相应的组内，可取比数据多一位小数来分组；列频数分布表，把数据划记到相应的组中，列表可采用唱票的方法进行频数累计；画频数分布直方图，各个“小长方形”之间应该是连续的，不应该有间隔. （2）内容解读：频数分布直方图的特点是能够显示数据的分布情况，易于显示各组之间的频数的差别；频数分布直方图实际上是用长方形的面积表示频数，当长方形的宽相等时，可以用长方形的长表示频数.

【变式1】原有条件不变，增加新问题：（1）每组的频率分别是多少？（2）请画出扇形统计图。

【变式2】在原有条件的基础上增加新条件：“八年级学生共有800人”，请估计全年级身高超过165cm的同学大约有多少人？

（1）完成该频数分布表；

（2）把频数分布直方图补全。

【说明】根据频数=频率×总数可以求得a=2；而根据频数之和为50和频率之和为1可以求得b=9，c=0.18，从而补全频数分布直方图如下。

【变式4】出示不完整的频数分布直方图和扇形统计图，结合统计图表完成下列问题：

（1）扇形统计图中，表示164.5～167.5部分的百分数是______；

（2）请把频数分布直方图补充完整；

（3）哪一个图能更好地说明一半以上的同学身高在158.5～167.5之间？哪一个图能更好地说明身高在158.5～161.5的同学多于身高在164.5～167.5的同学？

【说明】（1）用单位1减去其他所占的百分比即可；

（2）以第5组为基准算出总数：5÷10%=50，则第7组的人数为：50×14%=7（人），在频数分布直方图补完整图形；

（3）直方图能反映数据集中的趋势，扇形统计图能更好的显示出相应的百分比.

解答：解：（1）1-4%-6%-10%-16%-18%-26%-4%-2%=14%；

（2）第7组的频数=50×14%=7，如图：

（3）扇形统计图能很好地说明一半以上的同学身高在158.5～167.5之间；条形统计图（或频数直方统计图）能更好地说明身高在158.5～161.5的同学多于身高在164.5～167.5的同学。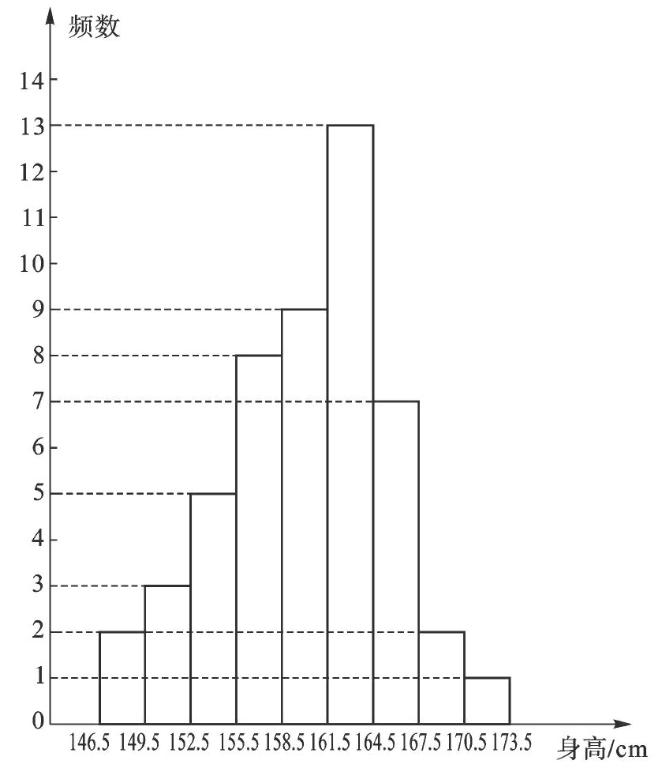

通过上面对教材中的一道例题的拓展和变式，不仅使我们初步完整地经历了数据的搜集、整理和描述的全过程，而且使我们明确了多种类型的统计图表的优劣，并根据信息互补解决相应的问题。