新型并网风电机组的动力学建模与仿真

武 鑫，苏 睿，芮晓明，陆从飞

（华北电力大学能源动力与机械工程学院，北京102206）

常见风力发电机组（简称风电机组）采用永磁发电机、双馈发电机，利用变频器等电力电子设备调速.随着单级容量的增加，风电机组存在的问题日渐凸显，包括谐波含量高、无功功耗大、变频器可靠性低等［1］.在此背景下，一些学者提出利用差动轮系等机械装置调速的风电系统，其末端采用同步发电机.

1994年，Mangialardi等［2］首次提出了利用差动齿轮箱对风电传动系统进行无级调速的方案.2000年，Idan等［3］进一步分析了差动调速风电系统的调速原理.2003年，Zhao［4］对该类风电系统的功率流向进行了研究.2008年，穆安乐等［5］分析了在全风速情况下各构件的角速度匹配关系.2009年，Claudio等［6］提出了利用带传动对风电机组进行调速的方案.2012年，王雪飞［7］使用bladed软件对差动调速风电系统进行了建模仿真并研究了调速电机的控制策略.

相关文献大多从运动学原理和控制策略的角度对采用差动调速的风电机组进行研究，但并没有对该类风电机组传动系统的动态特性进行深入探讨.鉴于此，笔者建立了差动调速风电机组传动系统的“弹簧-阻尼-质量”动力学模型，驱动2 500kW 的同步发电机并网运行，在Simulink环境下进行仿真，研究机组在阶跃风载荷驱动下的动态特性.

1 动力学模型

差动调速的风电机组主要由风轮、差动轮系、调速电机和同步发电机组成，系统框图如图1所示.差动轮系由太阳轮、轮架以及齿圈3个基本构件组成，风轮通过轮架轴连接轮架，调速电机通过齿圈轴连接齿圈，同步发电机通过太阳轮轴连接太阳轮.差动轮系自由度为2，只需限制其2个基本构件的转速，则另一基本构件具有确定的转速.

图1 差动调速的风电机组Fig.1 Structure of the wind tubine based on differential speed regulation

并网运行时，同步发电机转速（即太阳轮轴转速）被电网频率锁定，则调速电机转速与风轮转速为一一对应的关系.参考实时风速信号，求得使风能利用率Cp最高的风轮理想转速，并计算得到该理想转速对应的调速电机指令转速，从而实现调速电机调节风轮转速跟随最优Cp曲线.

1.1 总体三轴动力学模型

建立如图2所示三轴系统的动力学模型如下：

轮架轴

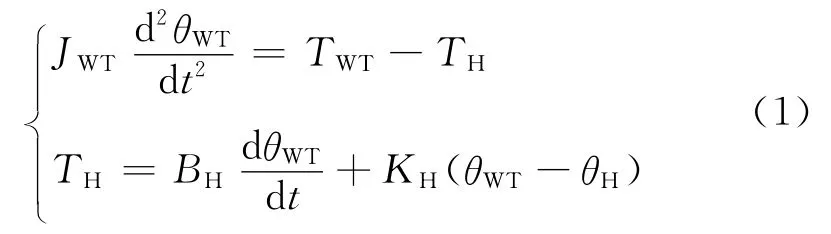
齿圈轴

太阳轮轴

图2 三轴系统结构示意图Fig.2 Tri-axial diagram of the system

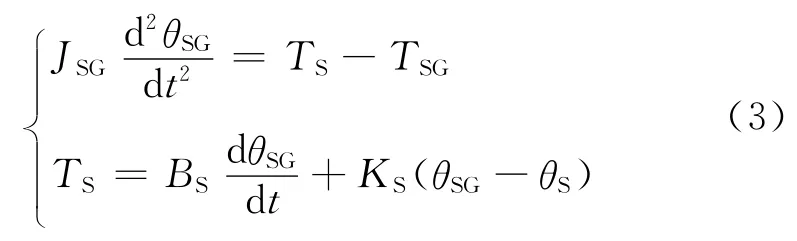
式中：JWT、JAM、JSG分别为风轮、调速电机和同步发电机的转动惯量；BH、BR、BS分别为轮架轴、齿圈轴和太阳轮轴的阻尼；KH、KR、KS分别为轮架轴、齿圈轴和太阳轮轴的刚度；θWT、θAM、θSG分别为风轮转子、调速电机转子和同步发电机转子的角位移；TH、TR、TS分别为轮架轴、齿圈轴和太阳轮轴的机械转矩；TWT、TAM、TSG分别为风轮转矩、调速电机电磁转矩和同步发电机电磁转矩.

根据能量守恒定律以及差动轮系调速原理，可得到三轴的转矩关系以及转速关系，如下式所示：

式中：u为差动轮系的结构参数，其值等于齿圈与太阳轮的齿数比；θH、θR、θS分别为轮架、齿圈和太阳轮的角位移.

1.2 风轮模型

风轮的数学模型可由下述方程组描述［8］：

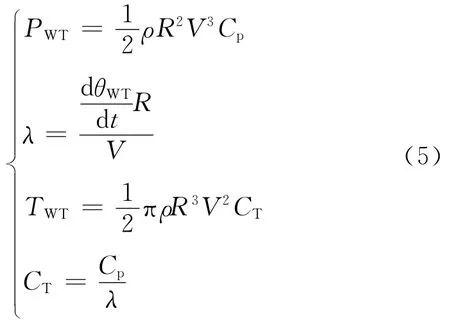
式中：PWT为风轮吸收的功率；R为风轮半径；ρ为空气密度；V为风速；λ为叶尖速比；Cp为风能利用率；CT为转矩系数.

Cp可由式（6）表示［9］：

式中：cy为升力系数；β为桨距角.

当风速超过额定风速时，应调节桨距角β来限制输入气动功率［10］，其一阶控制模型为：

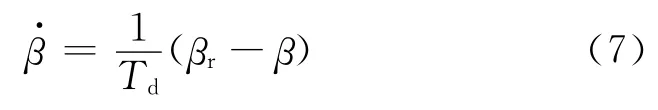
式中：Td为时间常数；βr 为桨距角参考值.

1.3 调速电机模型

调速电机由变频器驱动异步电动机构成.在按转子磁场定向的d-q旋转坐标系下，建立异步电动机动态数学模型［11］.

电压方程：

磁链方程：

电磁转矩方程：

式中：下标s代表定子参量，r代表转子参量；p为微分算子；u为电压；ψ为磁链；i为电流；L为漏感；R为电阻；np为极对数；Tr为转子机械转矩；Te为调速电机的电磁转矩；Lm为定转子互感.

1.4 同步发电机模型

同步发电机定子与电网直接相连，其转速被电网频率锁定，电磁转矩TeSG为：

式中：Uφ为端电压；EA为总电势；Xs为同步电抗；wm为转子机械转速；δ为转矩角.

2 仿真与分析

采用Simulink软件搭建仿真模型.选择2 500 kW 同步发电机并入电网，调速电机选择300 W 异步电动机，差动轮系的结构参数u＝40，轴刚度为5.6×106N·m／rad，轴阻尼为0.5N·m·s／rad.

风轮参数：半径为50 m，转动惯量为55 600 kg·m2.

调速电机参数：额定功率为300kW；转子的转动惯量为9kg·m2；定子电阻为0.014 85Ω；定子漏感为0.000 302 7H；转子电阻为0.009 295Ω；转子漏感为0.000 302 7H；互感为0.010 46H.

同步发电机参数：额定功率为2 500kW；额定转速为1 800r／min；额定转矩为13 264N·m；转子的转动惯量为100kg·m2.

采用如图3所示的阶跃风载荷作为输入，获得轮架轴、齿圈轴、太阳轮轴的转速、转矩以及功率.

图3 阶跃风载荷Fig.3 Curve of the step wind load

初始风速为12m／s，在t＝14s时增大风速，2s后达到13 m／s，考虑到调速电机的启动，故绘图时横坐标取t＝10～30s.轮架轴、齿圈轴以及太阳轮轴的转速、机械转矩和功率如图4～图6所示，其中NH、NR和NS分别代表轮架轴、齿圈轴和太阳轮轴的转速；PH、PR和PS分别代表轮架轴、齿圈轴和太阳轮轴的功率.

图4 轮架轴、齿圈轴以及太阳轮轴的转速Fig.4 Speed of the planet carrier shaft，ring gear shaft and sun gear shaft

在12m／s的风速下，同步发电机以额定转速稳定运行并输出额定功率，风速开始增大后，轮架轴传递的功率亦增大，同时采用2种途径来减小吸收的风功率：一是通过变桨改变风轮桨距角β；二是通过调速电机改变风轮转速以改变叶尖速比λ，如图4所示.这2 种途径都能减小风能利用率Cp.从图6可以看出，14s时，系统传递功率发生突变，但在1s后，同步发电机的输出功率回落到额定值.

图5 轮架轴、齿圈轴以及太阳轮轴的机械转矩Fig.5 Torque of the planet carrier shaft，ring gear shaft and sun gear shaft

分析三轴系统是否发生共振，对图5中三轴的转矩信号进行FFT 变换，得到其频谱图（图7）.

传动系统各轴的刚度相同（即K＝KH＝KR＝KS），阻尼相同（即B＝BH＝BR＝BS）.三轴各自的固有振动频率fn可由式（11）计算：

图7 轮架轴、齿圈轴以及太阳轮轴的转矩频谱Fig.7 Frequency spectrum of the planet carrier shaft，ring gear shaft and sun gear shaft

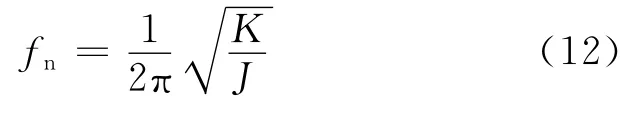
计算得到轮架轴、齿圈轴以及太阳轮轴的固有振动频率分别为1.537 6 Hz、39.700 2 Hz 和11.910 1Hz.避开了图7中的转矩频率分量，由此可知此系统在该阶跃风载荷驱动下不会发生共振.

3 结 论

（1）差动调速风电系统的同步发电机转速被电网锁定.在并网运行时，参考不同的风速，利用调速电机，结合差动轮系对风轮转速进行调节，从而获得预期的Cp值.

（2）建立了差动调速风电系统的三轴动力学模型，在阶跃风载荷下，各轴的机械转矩频率不同于各轴的共振频率.

（3）与调速电机相连的齿圈轴的载荷有不同频率的分布，故对调速电机的动态响应性能要求较高，应重点设计和选型.

［1］TERRYN C.Wind turbine design［M］.USA：Fer Publishing，2012.

［2］MANGIALARDI L，MANTRIOTA G.Automatically regulated CVT in wind power systems［J］.Renewable Energy，1994，4（3）：299-310.

［3］IDAN M，LIOR D.Continuously variable speed wind turbine transmission concept and robust control［J］.Wind Energy，2000，24（3）：151-167.

［4］ZHAO Xueyong.A novel power splitting drive train for variable speed wind power generators［J］.Renewable Energy，2003，28（13）：2001-2011.

［5］穆安乐，刘宏昭，张明洪.新型变速恒频风能转换系统的实现原理与运动学分析［J］.机械工程学报，2008，44（1）：195-204.

MU Anle，LIU Hongzhao，ZHANG Minghong.Theory and kinematics analysis of a novel variable speed constant frequency wind energy conversion system［J］.Chinese Journal of Mechanical Engineering，2008，44（1）：195-204.

［6］CLAUDIO R，PIERO C.W-CVT continuously variable transmission for wind energy conversion system［C］／／Proceeding of Power Electronics and Machines in Wind Applications.Lincoln，USA：PEMWA，2009.

［7］王雪飞.新型风机中调速电机的控制策略研究［D］.北京：北京交通大学，2013.

［8］刘小卡.水平轴风力机气动设计与实体建模［D］.上海：上海交通大学，2010.

［9］荆龙，王昕，汪至中.风轮机特性的模拟［J］.北京交通大学学报，2007，31（5）：110-113.

JING Long，WANG Xin，WANG Zhizhong.Simulation of the wind turbine［J］.Journal of Beijing Jiaotong University，2007，31（5）：110-113.

［10］任海军，何玉林.风力机变桨系统单神经元自适应PID 控制［J］.动力工程学报，2011，31（1）：22-26.

REN Haijun，HE Yulin.Single neuron adaptive PID control of wind turbine pitch systems［J］.Journal of Chinese Society of Power Engineering，2011，31（1）：22-26.

［11］胡虔生，胡敏强.电机学［M］.北京：中国电力出版社，2009.