核电站控制棒驱动机构隔磁片应力分析

曲大庄，李 晨，钱 浩，朱 宝，詹阳烈，景 益，刘 刚

（1.国家核电技术公司，北京100029；2.上海核工程研究设计院，上海200233；3.大连理工大学材料科学与工程学院，辽宁大连116024）

压水堆核电站通过改变或保持控制棒驱动机构组件在垂直方向上的位置来实现反应堆的启停、正常工况下堆芯功率的调节或保持以及事故工况下的快速释棒停堆.控制棒驱动机构的主要部件为：承压壳体部件、钩爪部件、磁轭线圈部件、驱动杆部件、导磁半环和导向隔热套等.位于壳外的磁轭线圈通电后将产生电磁场并带动装在壳内的部件（钩爪部件、驱动杆部件）步跃运动，使衔铁直线向上运动直至撞击到由磁极支撑的隔磁片上.当磁轭线圈断电电磁场消退时，衔铁在自重和弹簧力的作用下脱离隔磁片竖直向下运动，设置在磁极和衔铁之间的隔磁片起到了加快机构释放速度的功效.

为满足反应堆启停及功率调节的需要，控制棒驱动机构在设计寿期内要经历数百万次的步跃运动，对于大部分设计寿命在40年左右的第二代核电技术，步跃约为200万步；而设计寿命在60年的第三代核电技术则要求600万步.在过去的运行经验中，控制棒驱动机构的主要失效形式是钩爪部件销轴和销轴孔的磨损所引起的失步和滑步，但随着控制棒驱动机构设计寿命的大幅度提高，除了原有的失步、滑步失效形式外，又发现了隔磁片在一定次数步跃运动后的疲劳破损现象，已经引起业界的高度关注.

在控制棒驱动机构的实际工作过程中，对于驱动机构的每一次步跃运动，磁轭线圈的电磁场都会使衔铁撞击隔磁片，使隔磁片不断受到冲击载荷.在结构上，隔磁片为具有内、外径的轴对称薄壁圆盘，其法平面的一侧始终与磁极接触（或分离），另一侧的内径区域始终与压紧弹簧紧密接触，外径区域则受到衔铁撞击的冲击载荷.显然，准确分析隔磁片在衔铁冲击载荷作用下的应力分布及具体数值，对于控制棒驱动机构的安全设计及寿命预估显得尤为重要.如文献［1］中将应力分析的结果应用到疲劳安全性分析中.

笔者根据弹性力学［2］板壳理论建立了隔磁片在衔铁冲击载荷作用下的基于磁极弹性基础的薄壁圆盘轴对称弯曲应力分析模型，直接利用幂级数给出了微分方程的解析式.由于作用在隔磁片上的载荷沿径向并非连续，与磁极的接触在一般情况下也不一定连续，因此需要将隔磁片沿径向分解成几个圆盘，根据分界处内力平衡和位移连续条件，利用传递矩阵技术建立了整体平衡方程，并根据隔磁片内、外径的自由边界条件得到了问题的全部解.

利用所提出的方法对某在建核电站控制棒驱动机构的隔磁片在衔铁撞击达到最大冲击载荷时的工况进行了应力分析计算，得到了相关的应力分布和具体数值，与有限元数值计算结果进行了比较，并通过已经出现的隔磁片冲击疲劳破损事例的验证，为核电站控制棒驱动机构的结构设计以及隔磁片的冲击疲劳和失效机理等分析提供了理论依据.

1 薄壁圆盘轴对称弯曲的微分方程及解析解

若将隔磁片简化成如图1所示的置于磁极弹性基础的薄壁圆盘，当法向载荷为q，基础弹性系数为ks时，令w为圆盘的法向位移，为圆盘的平均半径，并且r＝x，＝q，＝ks，则有圆盘轴对称弯曲的微分方程为

式中：D为圆盘弯曲刚度，且；μ为泊松比；h为圆盘厚度；E为圆盘材料弹性模量.

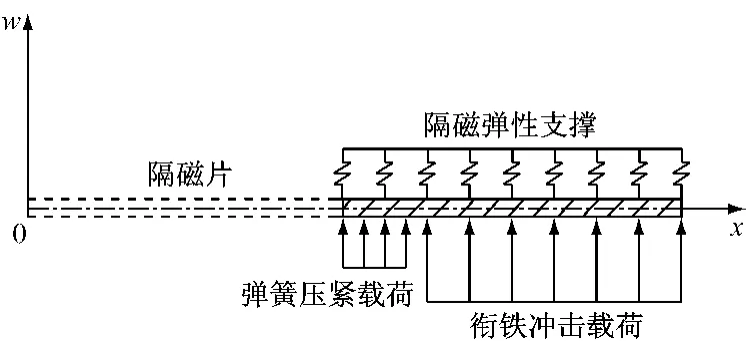
图1 隔磁片轴对称薄壁圆盘Fig.1 Axisymmetrical thin disk of the magnetic isolation shim

式（1）的求解与隔磁片和磁极是否接触有关.当二者分离时，即ks＝0时式（1）的全部解可直接由弹性理论分析结果得到，即（，为常数）

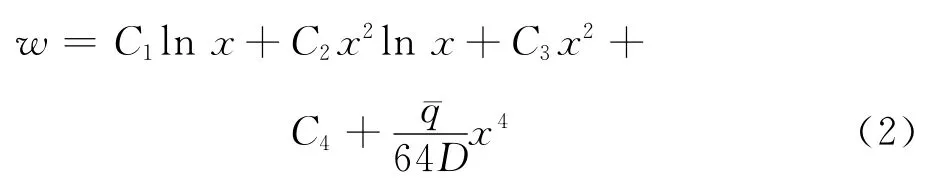
式中：C1～C4为待定系数.

当隔磁片与磁极有接触，即ks≠0 时，虽然式（1）已有基于Bessel特殊函数的经典解［3-4］，但为了数学上的方便，还可以直接采用幂级数解，即

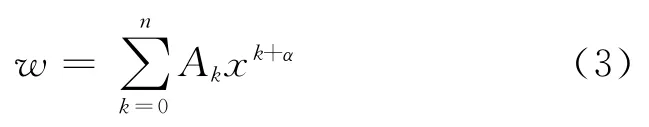
根据式（1）的齐次方程以及待定系数α应满足的条件，可得到对应于A0≠0，A1＝A2＝A3＝0 时的α1＝0，α2＝2.将α1和α2分别代入式（3），可得式（1）的2个线性无关解

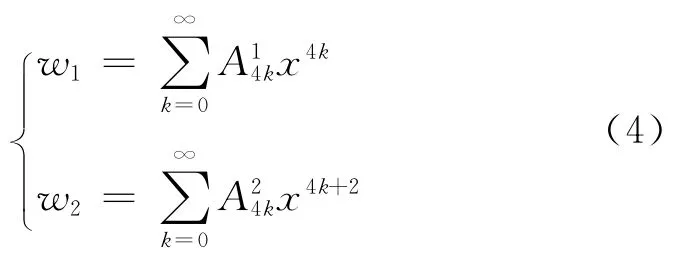
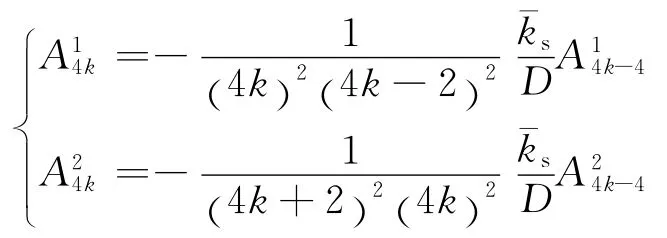
由于式（1）是一个4阶方程，需要有4个线性无关解来构成其通解，因此可仿照求解Bessel方程［5］的方法给出另外2个线性无关解，即

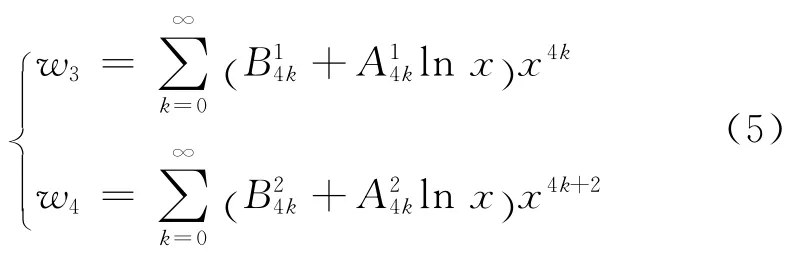
式中：

式（1）的特解取决于载荷的分布形式，当其为常数时，有.与式（3）线性组合得到式（1）的全部解

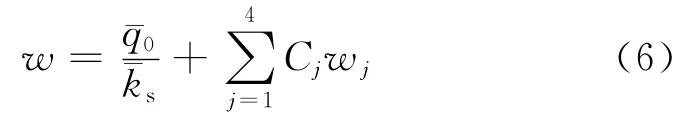
显然，式（2）或者式（6）分别给出的便是隔磁片在法向载荷q作用下与磁极分离或者接触时薄壁圆盘轴对称弯曲的微分方程的解析解.

2 隔磁片状态向量的传递及整体平衡方程

根据隔磁片上弹簧压紧载荷和衔铁冲击载荷沿径向的分布情况以及与磁极弹性支撑的接触情况，可将隔磁片沿径向分解成几个薄壁圆盘.对于其中的任何一个均可定义其边界上的物理量，，，并根据圆盘轴对称弯曲时位移w与转角φ、弯矩M和剪切力F的关系（式（7））

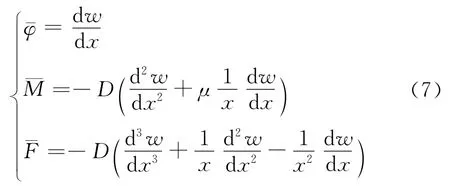
结合式（2）或者式（6）建立隔磁片分段后各段的状态向量方程

式中：

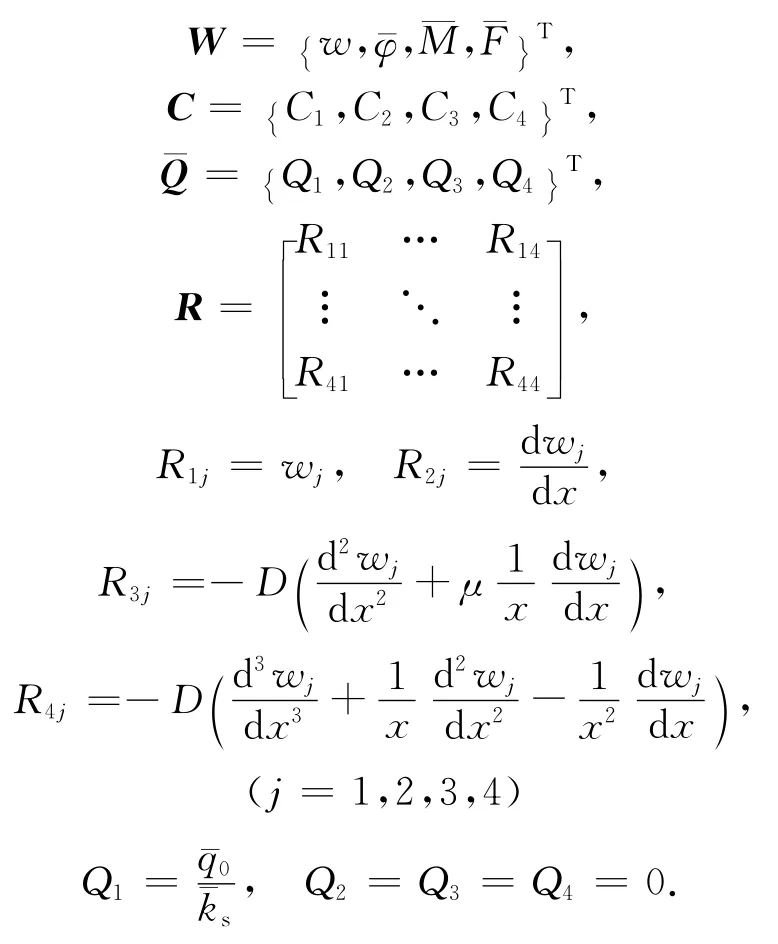
当把隔磁片分解为m段时，可根据第k段内、外径r0和rn处的状态向量和，定义传递矩阵，得到同一段圆盘内、外径两端的状态向量关系

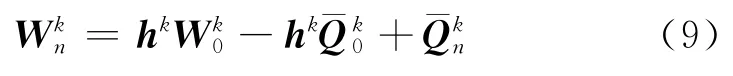
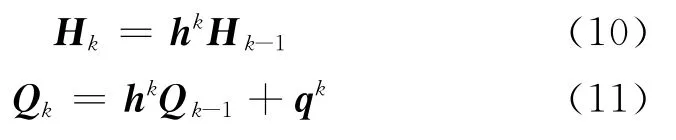
遍取k＝1，2，…，m，最终得到隔磁片整体内、外径两端的状态向量关系，即隔磁片应力分析的整体平衡方程

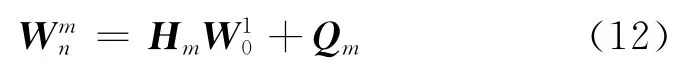
由于隔磁片内、外径两端的边界条件为自由状态，即当r＝r0时，M0＝F0＝0，以及当r＝rm时，Mm＝Fm＝0，因此将它们带入上式可以得到

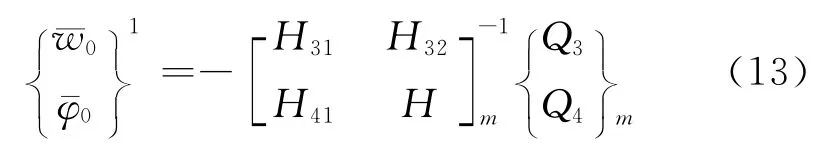
利用式（9）的传递关系，可最终确定各分段界面处的状态向量，以及各段内不同径向位置r＝ri的状态向量.

除前述隔磁片状态向量中M所代表的径向弯矩Mr外，在圆盘轴对称弯曲问题中还有切向弯矩Mθ.根据

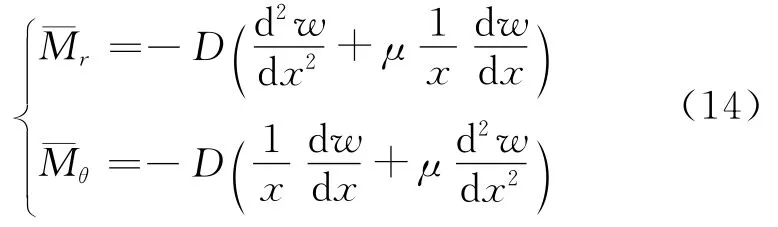
并考虑到＝dw／dx，有关系式

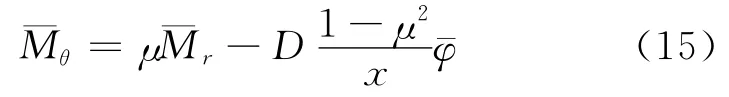
进而得到隔磁片上下表面处的径向弯曲应力σr和切向弯曲应力σθ

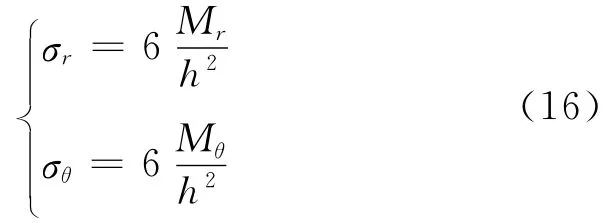
其中，σr和σθ都是径向位置的函数.

3 隔磁片应力计算结果以及与有限元数值计算结果的比较

利用笔者提出的方法对某在建核电站控制棒驱动机构的隔磁片在衔铁撞击达到最大冲击载荷时的工况进行应力分析计算，相关数据为：隔磁片内径r0＝30.70mm，压紧弹簧处外径r1＝37.00mm，衔铁处内径r2＝39.40 mm，隔磁片外径r3＝63.25 mm，圆盘厚度h＝1.59 mm，材料弹性模量E＝1.90×1011N／m2，材料泊松比μ＝0.3，磁极支撑弹性系数ks＝1.35×1012N／m3，弹簧压紧载荷Pz1＝480N，衔铁最大冲击载荷Pz2＝6.11×105N.为了比较，采用Ansys有限元分析软件中轴对称壳单元和弹簧单元对同样的隔磁片分析模型进行了最大冲击载荷下的应力计算.有限元分析隔磁片采用Shell208 轴对称壳单元模拟，弹性支撑采用Combin14线性弹簧模拟.有限元分析模型和边界条件如图2 所示，对Combin14弹簧单元弹性支撑端节点约束隔磁片法向位移自由度.载荷条件如图3所示.所有输入参数与第2节理论公式计算参数一致.

图2 有限元分析模型和边界条件Fig.2 FEA model and boundary conditions

2种分析方法的计算结果同时示于图4～图7，从图中可以清晰地看到二者完全吻合.

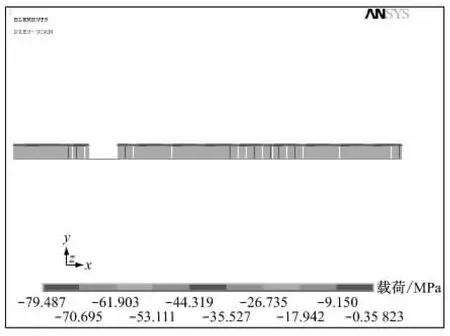
图3 载荷条件Fig.3 Loading conditions

图4 法向位移Fig.4 Normal displacement

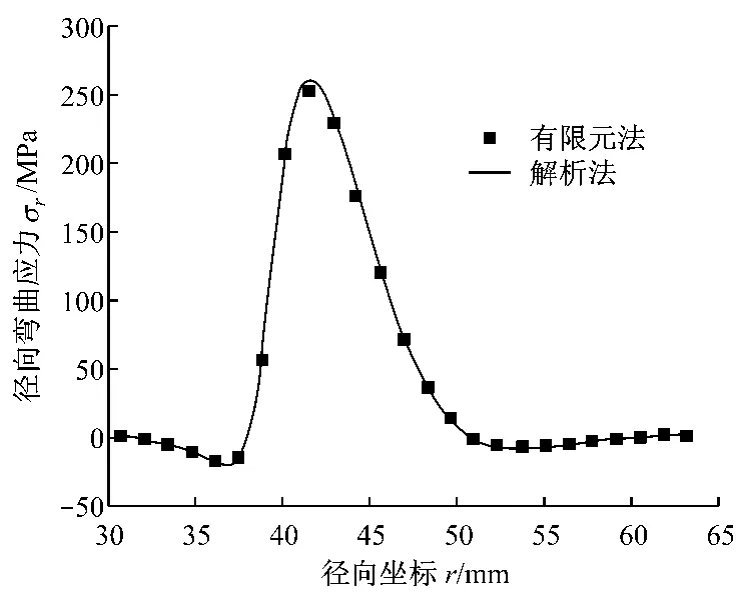
图5 径向弯曲应力Fig.5 Radial bending stress

如图4所示，衔铁撞击到隔磁片冲击载荷达到最大值后，隔磁片在内径r＝36.2 mm 附近与磁极发生分离，或者说虽然有压紧弹簧，但在最大冲击载荷时它不能保持隔磁片始终与磁极相接触.

与隔磁片冲击疲劳相关的拉应力发生在隔磁片与磁极接触侧，图5和图6分别给出了该侧隔磁片的径向和切向弯曲应力，在半径r＝42.0 mm 附近二者均出现最大值σr＝259 MPa、σθ＝58 MPa.图7给出了隔磁片与磁极之间的轴向压应力，最大值约为σz＝82 MPa.

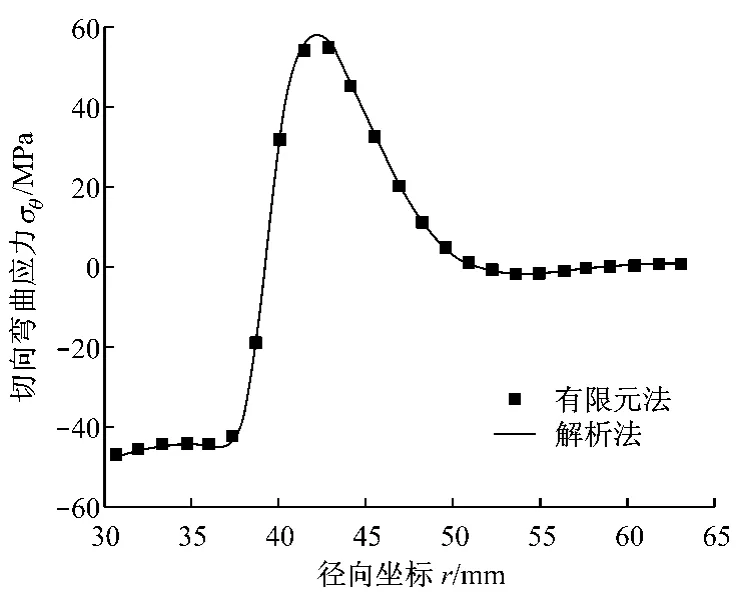
图6 切向弯曲应力Fig.6 Tangential bending stress

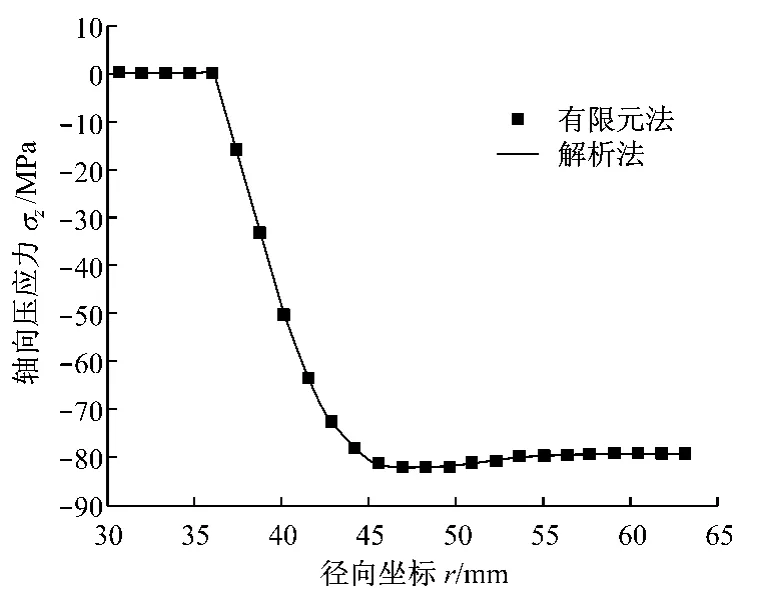
图7 轴向压应力Fig.7 Axial compressive stress

对于隔磁片的冲击疲劳，可根据材料疲劳最大变形能理论［6］确定疲劳等效应力

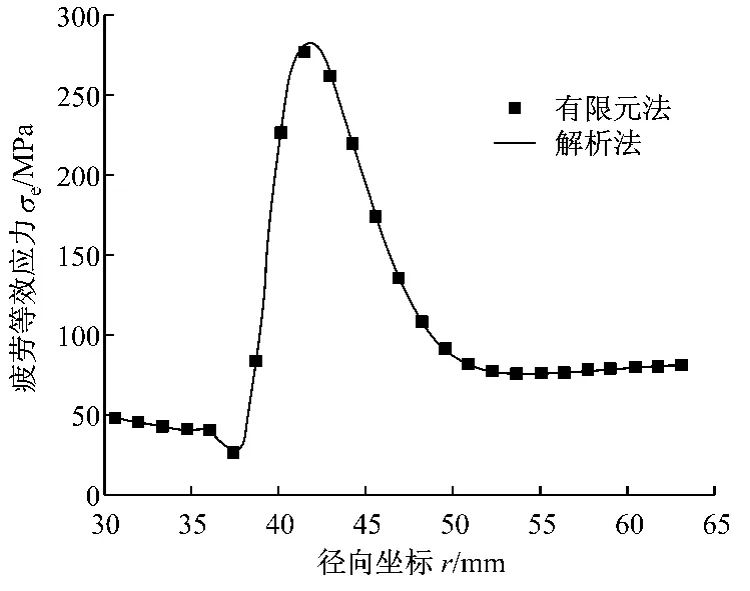
图8 疲劳等效应力Fig.8 Equivalent fatigue stress

图8给出了将各应力分量结果代入上式所得到的疲劳等效应力.从图8可以看出，最大疲劳等效应力σe＝283 MPa，发生在距离内径约1／3隔磁片径向宽度处，它以径向拉应力σr为主体，是导致隔磁片经历一定次数步跃运动的衔铁冲击载荷作用后出现疲劳破损的主要原因，与隔磁片冲击疲劳破损事例裂纹的起始位置和扩展模式相符.

4 结 论

（1）虽然有压紧弹簧，但隔磁片不能始终与磁极保持接触，在衔铁最大冲击载荷作用下，隔磁片将产生弯曲变形并在压紧弹簧附近与磁极发生分离，导致与磁极接触侧出现与冲击疲劳相关的弯曲拉应力.

（2）隔磁片与磁极接触侧处于三维应力状态，可根据材料疲劳的相关理论确定相应的疲劳等效应力.以径向拉应力为主体的最大疲劳等效应力发生在距离内径1／3隔磁片径向宽度处，它是导致隔磁片经历一定次数步跃运动的衔铁冲击载荷作用后出现疲劳破损的主要原因.

（3）所提方法的分析结果与隔磁片冲击疲劳破损事例裂纹的起始位置和扩展模式相符合，可以为核电站控制棒驱动机构的结构设计以及隔磁片的冲击疲劳和失效机理等分析提供理论依据.

［1］史进渊，邓志成，汪勇，等.汽轮机转子初始裂纹高周疲劳安全性分析方法及其在焊接转子中的应用［J］.动力工程学报，2013，33（1）：17-24.

SHI Jinyuan，DENG Zhicheng，WANG Yong，etal.High cycle fatigue safety analysis for steam turbine rotors with initial crack and its application to a welded rotor［J］.Journal of Chinese Society of Power Engineering，2013，33（1）：17-24.

［2］徐芝纶.弹性力学［M］.北京：高等教育出版社，2006.

［3］黄义，何芳社.弹性地基上的梁、板、壳［M］.北京：科学出版社，2005.

［4］杨奇林.数学物理方程与特殊函数［M］.北京：清华大学出版社，2011.

［5］铁摩辛柯S，沃诺斯基S.板壳理论［M］.北京：科学出版社，1977.

［6］铁摩辛柯S.材料力学［M］.北京：科学出版社，1979.