多视角审视下的圆锥曲线教学

梅永常

近几年广东高考的圆锥曲线的考查，考生得分率一直较低，要在这版块里有真正的改善，提升学生解决圆锥曲线问题的能力，需要在多视角下重新审视，下面结合具体的例子加以说明.

圆、椭圆、双曲线和抛物线同属于圆锥曲线.早在两千多年前，古希腊数学家阿波罗尼（Apollonius）采用平面切割圆锥的方法来研究这几种曲线.他用垂直于锥轴的平面去截圆锥，得到的是圆；把平面渐渐倾斜，得到椭圆，当平面和圆锥的一条母线平行时，得到抛物线；当平面再倾斜些时就可以得到双曲线.

在中学的教学中，圆锥曲线的这个奇妙的来源令学生很好奇，而用代数研究几何，采用是是容易明白、方便建系的定义，如果在导向上把握不好，很容易导致过多地模式化的代数技巧演练，学生对几何特质的视角逐步变窄，令本来充满鲜活性的圆锥曲线问题变得索然无味.所以要真实地回归几何定义，精心设计，引导学生进入圆锥曲线的奇妙之旅.

学生学完椭圆后，在进入双曲线学习时，笔者尝试以课本的课后练习题（人教A版2-1P62-6）作为引入，收到很好的效果.

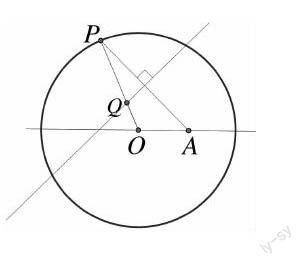
例：如图，圆O的半径为定长r，A是圆内一个定点，P是圆是任意一点，线段AP的垂直平分线l和半径所在直线交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？

视角1：因为刚刚学完椭圆，学生很快就发现到点Q的几何特征：

|QA|+|QO|=|PQ|+|QO|=|PO|=r>OA.

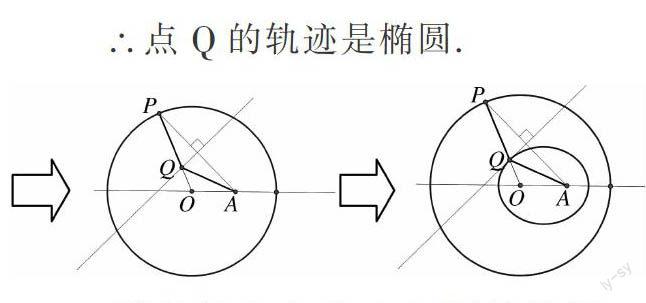
∴点Q的轨迹是椭圆.

视角放在在点A与圆的位置关系上，提出问题：如果定点A在圆上，会发生什么事？

问题一出，学生的思维受到激发，很快发现这种情形下，Q点总是与圆心重合，从而轨迹为一点.

在好奇心的驱使下，学生很自然地提出第二个问题：如果定点在圆外，点Q的轨迹又会是什么？

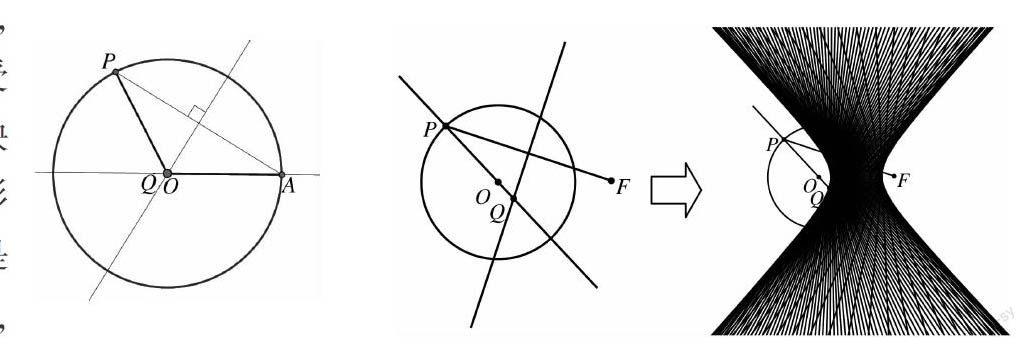
类比下，学生不费多大工夫发现了点Q的几何特征：|QA|-|QO|= |PO|=r.当然，较多学生容易漏了另一种情形：|QO|-|QA|=|PO|=r.

继续点拨下，双曲线的几何特征就出来了：||QA|-|QO||=|PO|=r< |OA|.

整个过程在学生的积极想象和观察下，再借助《几何画板》的辅助演示，既达到巩固椭圆定义、和熟悉双曲线的作用，也为两种曲线搭上了很好的桥梁.

视角2：不谋而合的是，苏教版教材2-1（P43-11）也有类似的一道题：在纸上画一个圆O，在圆外任取一点F，将纸片折起，使圆周通过F，然后展开纸片，得到一条折痕l（为了看清楚，可以把直线l画出来），这样继续下去，得到若干折痕，观察这些折痕围成的轮廓，它是什么曲线？

很显然，苏教版教材着眼于让学生通过操作得到轨迹，非常直观实用，如果敢于实践，学生对轨迹特征的认识应该更深刻.

圆锥曲线具有丰富的几何特性，就定义本身，就玄妙无比，教学中，就要启发学生去观察，通过问题的设置，激发求知欲，提升思考力.要学生克服对圆锥曲线的畏惧情绪，就要引领学生逐步形成自己独特的解题视角，学会欣赏问题，一定的积累，形成对圆锥曲线的审美能力，解题也就水到渠成.

责任编辑罗峰