统计总体的3种形式及其在体育科研中的地位和作用

魏登云，吴家发



●体育科学研究方法Method of Sport Scientific Research

统计总体的3种形式及其在体育科研中的地位和作用

魏登云，吴家发

摘要统计总体在体育统计应用中具有重要作用，对统计总体的全面和深刻认识关系到统计方法的正确应用。从体育科研的实际出发，提出统计总体的3种形式：原总体、数量化总体和模型化总体。3种形式总体的特征各有不同：原总体个体同质性，数量化总体个体差异性，模型化总体个体同分布。3种形式总体的地位和作用各不相同：原总体是定量分析的出发点和归宿，对统计方法有引导作用，对统计处理结果起决定作用；数量化总体是研究目的的操作化，是量的规律的承载体，也是样本数据的母体；模型化总体则是统计规律的反映形式，是揭示统计规律的必要手段。确定总体时需要重点把握确定试验对象的共同属性、准确体现研究变量的价值信息和正确把握随机变量及其分布模型3个方面。

关键词统计总体；试验；变量；概率分布；共性特征；个体差异

统计总体是统计学的基本概念，无论是数理统计学，还是应用统计学，统计总体都无可争辩地被视为最重要的概念。一般看来，作为概念，总体不难解释，各类教科书中关于总体的定义基本上一致。但在应用领域面对具体问题，需要明确总体是什么的时候，难度远比想象的大。因为实际问题错综复杂，总体的内容和形式多样，针对一个具体问题，关于“总体是什么”的问题，人们的理解和看法出现了分歧，由此引发了激烈争议[1-6]，甚至波及到对“什么是总体”的重新审视。在体育科研中，由于总体不明确，导致的问题也确实不少[7]。

实际上，在体育统计方法应用中，总体的地位和身份很特殊，她既是研究目的的操作化体现，又与研究手段相关联，还在统计结果中扮演着重要的角色。在不同的工作环节中，总体的表现形式不同，不同形式的总体各有其实际价值，不能互相替代，但又是统一的。如果对总体的内涵认识模糊，混淆总体的表现形式，将会导致统计方法的应用错误，而且错误之处不容易被发现。

本文拟从体育科研的实际出发，讨论总体的形式、不同形式总体的价值以及应用中如何把握总体。

1　总体的形式

什么是总体？作为概念，人们对总体的定义是基本一致的：根据研究目的所确定的对象的全体。但是针对某一个具体问题，总体是什么？在统计学文献中有不同的描述。如研究某工厂生产的电子元件的寿命，总体是“该工厂生产的电子元件的全体”，其中每一个单个元件是一个个体，这里的总体是一批“物”的全体；总体也可以是“该工厂生产的电子元件寿命的全体”，个体是单个元件的寿命，这里的总体是一批“数”的全体；该工厂生产的电子元件的寿命是一个变量，总体还可以描述为“具有某种概率分布的一个随机变量”[8-9]。同一个具体问题，总体为什么有或为什么需要有不同的描述，这正是本文的研究目的。关于总体的不同描述，实际上是具体应用中总体的不同形式。实际应用中，总体有3种形式，为了表述方便，分别称之为原总体、数量化总体和模型化总体。

1.1原总体

运用统计学原理和方法解决实际问题，首先就要根据研究目的确定与所研究问题有关的对象。如观察对象、测试对象和实验对象等，统称为试验对象。具体问题中，试验对象可能是人、物、现象或行为等。所有试验对象的全体，称为原总体，其中的每一个试验对象称为个体。原总体不考虑课题研究的指标，只关心试验对象的同质属性。

例1：研究安徽省成年男子的身高分布状况。

原总体是安徽省所有成年男子的全体，每一个成年男子是一个个体，这里的原总体是一类“人”的全体。

例2：研究某人的篮球投篮命中率，令其在相同条件下重复投篮若干次。

这里研究者关注的“对象”不是这个“人”，而是此人的“投篮”现象。所以，原总体是此人在相同条件下所有可能的重复投篮的全体，个体是其中的一次投篮。

需要说明的是，例2中的总体是“无穷多次投篮的全体”，而不是“无穷多次投篮结果的全体”。“投篮”与“投篮结果”是不同的，“投篮”是一次行为或现象，而“投篮结果”是一种可以量化的结果，这正是原总体与数量化总体的区别。

1.2数量化总体

实际问题尽管多种多样，但从定量分析（尤其是统计学）的角度看，研究目的无非是分析“在某一类对象上，某些变量（在一般统计学著作中也称指标或项目，在经济、管理类统计学中，称为标志，而指标却另有指称，为了避免误解，本文称为变量）的分布情况”或“某些变量在某类对象上的规律”。涉及到2大要素，即“对象”和“变量”。原总体已经把全体“对象”包罗起来，那么研究目的就是分析变量在原总体上的分布或规律，此时自然要考虑变量在原总体上的实现，即原总体的数量化。经过量化，原总体中的每一个个体都被赋予一个或一组变量值，所有个体“变量值”的全体也是总体，称之为数量化总体，其中每一个个体“变量值”称为个体。

例1中，数量化总体是安徽省成年男子身高的全体，每一个人的身高值是一个个体。这里，课题研究的指标是身高，数量化总体是试验对象具体到“指标”的结果。

例2中，被关注的变量是“投篮结果”，该变量只取2个值，即“投篮命中”和“投篮不中”（实际应用中通常以1和0表示2种结果），原总体中的个体“变量值”就是1或0。从形式上看，数量化总体是由无穷多个1和0构成的，用语言描述为“此人在相同条件下所有可能的投篮结果的全体”。

1.3模型化总体

数量化总体是变量在原总体上“实现”的结果，变量在原总体上的分布规律完全蕴含在数量化总体中。但是，数量化总体毕竟是“个体集合”的形式，而且多数情况下数量化总体中的个体数是有限的，有限总体的分布形式只能是离散的，难以用简洁的数学形式来表述。于是，统计学家引进了“无限总体”的概念，从而用连续型分布去逼近离散型分布。

例1中，数量化总体只有有限个个体（有观测时间约定），却可以说“安徽省成年男子的身高服从正态分布”，就是用正态分布来逼近有限总体的分布。这就相当于，用一个理想化的分布模型去逼近一个现实总体的分布，这种理想化的分布模型也叫做总体，称之为模型化总体。因为，概率分布肯定是指某个随机变量（或随机向量）的分布，所以模型化总体通常又以一个随机变量或随机向量来代表。随机变量（向量）作为总体的一种形式，实质上是对总体分布的模型化。

例2中，数量化总体形式如{0，1，1，0……}，“投篮”所表现的随机现象的规律蕴含其中。该总体中的个体非1即0，总体的分布实质上是1和0出现的频次分布，如果以X代表只取1和0 2个数值的变量，则随机变量X的概率分布便是总体的分布。实际上，此时X的概率分布是典型的“2点分布”概率模型[8]。至此，例2中的研究目的实质上是对服从“2点”分布的随机变量的统计推断，随机变量X就是该问题的模型化总体。

2　3种形式总体的比较

2.13种形式总体的区别

2.1.1总体形式不同从形式上看，原总体和数量化总体都是个体集合形式，构成总体的方式是罗列所有的个体；模型化总体则是随机变量或随机向量的形式，不再罗列总体中有哪些个体，只是将数量化总体中不同的个体象征性地提出来。需要说明的是，随机变量所有可能取值的全体不等于数量化总体。如例2数量化总体由无穷多个1和0构成，是无限总体，而随机变量X所有可能取值的全体是集合{1，0}，模型化总体不是集合{1，0}，而是服从“2点分布”的随机变量。

2.1.2总体特征不同 （1）原总体的个体同质性。原总体是试验对象的全体，这些试验对象之所以构成一个总体，必有其共同的特征或属性，即个体同质性。如例1中，原总体是“安徽省所有成年男子的全体”，其中每一个个体都有共同的属性，即安徽省、成年人和男性。原总体中所有个体都是同质的，不同的原总体肯定有不同的质，“质”的内容在实际问题中自有规定。（2）数量化总体的个体差异性。数量化总体是变量在原总体上“实现”的结果，其个体是变量在原总体中个体上的一个实现（即变量值），个体之间有差异。如果某一个变量在某个原总体上没有差异，那么该“变量”在该总体上是常量。实际应用中，常量是不会作为统计分析对象的，充其量是原总体的一个同质特征。统计分析的主要目的是研究变量在原总体上的规律，正因为变量在原总体上有差异，才需要做统计分析。如果说，原总体反映个体的同质性，那么数量化总体则关注个体之间的差异性。（3）模型化总体的抽象化和理想化特征。模型化总体不考虑具体的个体，只表示总体的分布，即随机变量或随机向量的概率分布。模型化总体的分布，是从实际问题中抽象出来的理想化的概率分布模型。如例1中，模型化总体是一个服从正态分布的随机变量，正是数量化总体分布的理想化结果；例2考虑的是某人的投篮命中率，如果研究某市中学生的近视率、某个排球队的发球得分率等，模型化总体都是服从2点分布的随机变量，这些具体问题形形色色，但总体分布的模型是一类的，体现出模型化总体的抽象化特征。

2.1.3总体信息不同从信息的角度看，原总体表明试验对象的共性特征或属性，即“质”的内容，除此之外，看不出其他信息；数量化总体，蕴含着变量在原总体上的所有信息，包括个体信息和各种分布信息，但数量化总体是“数”的全体，原始对象的共性特征或属性在数量化总体中是看不出来的；模型化总体，是对数量化总体中有关分布信息的反映或描述，只关注有关变量的分布信息，而且模型化总体所表达的信息与数量化总体中的真实信息未必完全一致，前者有人为加工的成分，模型化色彩较浓。

2.23种总体形式的联系

2.2.1原总体是数量化总体的前身原总体是所有试验对象的全体，数量化总体是原总体“量化”的结果，二者的个体是一一对应的，从结构上看，两者完全一致。但原总体是前提，没有明确的原总体，就没有具体的数量化总体。

2.2.2数量化总体是模型化总体的源模型化总体是对数量化总体中“量”的规定的一种提炼，数量化总体的分布规律通过模型化总体反映出来，如果说原总体和数量化总体带有明显的目的性的话，那么模型化总体则是工具性的，没有数量化总体，当然也就不需要模型化总体。

原总体、数量化总体和模型化总体是随着实际分析问题的推进，不同时段的总体表现形式，三者的关系见图1。

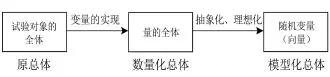
图1　3种形式总体的流程图

3　3种形式总体的地位和作用

总体的3种形式尽管统一于“对象的全体”，但在实际应用中，三者的作用各不相同，不能相互替代。

3.1原总体的基础地位和作用

3.1.1定量分析的出发点和归宿前面提到，定量分析的2大基本要素是“对象”和“变量”，明确“对象”是课题设计的首要环节。原总体作为试验对象的全体，在明确所有对象共同属性的同时，也规定了总体的范围，为保证样本的同质性提供了必要的基础。站在抽样的角度，原总体是样本的唯一来源，这是数量化总体和模型化总体所无法替代的，因为只有原总体明确了试验对象“质”的规定。

原总体也是定量分析结果应用的对象，原总体界定了抽样的范围，自然也就规定了分析结果的使用范围，这在实际应用中是非常重要的。实际工作中，人们往往关注的是数量化的样本，而疏于对原总体的重视。其实，多数情况下原总体才是目的。

3.1.2对统计方法的引导作用原总体对统计方法的选用有重要影响。同样的问题，选择的原总体不同，采用的统计方法也不一样。

例3：体操比赛中，6位裁判员同时、独立地给某个运动员评分，6个评分结果不尽相同，该运动员的最终成绩如何确定？

目前，国内外比赛通用方法存在的问题在已有研究[10]中已有详细阐述，这里提出2种原总体，用以说明对处理方法的影响。（1）总体1：符合规定要求的所有裁判员的全体。现场执裁的6位裁判员是一个样本。（2）总体2：现场执裁的6位裁判员无穷多次评分（对1个运动员）的全体。6位裁判员的现场评分（每人1次）视为来自总体的一个样本。

总体1是常见的，也颇为自然，如果按这个总体和样本，运动员最终成绩确定为6位裁判员评分结果的平均数。因为，样本平均数是总体均值的最优估计量。事实上，这里用6个评分结果的平均数作为运动员最后得分是不合适的。

总体2中，蕴含着“6位裁判员评分的权重不尽相同”，已有研究[11]据此给出了运动员最后得分的估计方法。

总体不一样，处理方法截然不同。

3.1.3对统计处理结果的决定作用有时候原总体不同，即使同样的处理方法，结果也相差甚远。

例4：某人研究30个身体素质项目的内在结构，希望简化指标。请20位专家对30个项目的重要性进行评分，然后对获得的评分数据进行主成分分析，得到8个主成分，认为30个指标被压缩成了8个。

该处理结果是有问题的，相关研究[12]针对类似情况，从认知数据的角度分析了其中的问题所在，这里从总体的视角透视其中的原因。

由数据来源不难看出，例4中原总体是“某一类专家的全体”，20位专家被视为一个样本。主成分分析的实质是揭示变量之间的关系，而专家是对每个项目的“重要性”进行评分，并非评价各个项目之间的关系。事实上，若要专家对30个项目之间的关系作主观评价也确实是强人所难。所以，基于这样的数据作主成分分析，得到的结果是难以揭示变量之间的关系的，至少达不到研究目的。

根据研究目的，例4中的原总体应该是“能够客观反映30个身体素质项目真实水平的某一类运动员的全体”，样本是随机抽取的部分运动员。

例4中的问题隐蔽性很强，从数据形式上很难看出弊端。从源头来看，问题就出在原总体的选择上，原总体不合适，再高级的统计处理方法也难以得出可靠的结果。

3.2数量化总体的特殊地位和作用

原总体明确了所有对象及其共同特征，但没有变量的任何信息。数量化总体是原总体与变量的结合体，是原总体经过量化的结果，明确数量化总体是定量研究的必要环节。

3.2.1明确数量化总体是研究目的的操作化从工作环节上看，原总体的量化包括变量的确定和变量的实现2部分，其中，变量的确定是主要工作。实际工作中，研究目的往往比较笼统，甚至比较抽象，需要由某些变量来具体化。如学习能力、综合素质和训练效果等，都要以某些具体变量来反映或衡量，这是研究目的操作化的重要组成部分。仅有变量尚不能完整地反映研究目的，变量需要落实到原总体上（即在原总体上实现），才能具体地体现研究目的。数量化总体恰恰是研究目的操作化结果的体现，数量化总体用量的语言来表述研究目的，将实际问题用量的形式来显示。

例5：检验某种新训练方法的效果，考虑与传统训练方法作比较，采用配对实验设计。

研究目的很明确，即检验新训练方法相对于传统方法效果是否显著。原总体：该训练方法适用范围内的所有人（运动员或学生）的全体。变量的确定：针对该运动项目，选择能反映训练效果的有效变量，可以是一个变量，也可能是几个变量，不妨以X（也可以是向量）表示。传统训练方法的效果以X0表示，新方法效果用X1表示。针对研究目的，新方法相对于传统方法的效果体现在2种效果的差值上，即X1-X0，所以最终考虑的变量是X1-X0。变量的实现：对于原总体中的某一个个体，若按传统方法训练效果是x0，新方法训练效果是x1，2种方法的效果差x1-x0是变量X1-X0在该个体上的实现，即观测值。数量化总体：原总体上所有差值的全体。数量化总体明确后，本例的具体研究目的为：检验数量化总体的平均值是否为0。

3.2.2数量化总体是量的规律的承载体定量分析的最终目的是，研究有关变量在原总体上的分布规律或特征，数量化总体是变量在原总体上实现的结果，变量的所有价值信息全面蕴涵于数量化总体之中。明确了数量化总体，实际问题的探讨就归结为对数量化总体的分析。至此，数理方法得以有用武之地，这或许是数量化总体作为“总体”最有说服力的理由。

退而言之，统计学研究随机现象的内在规律，通过重复随机现象来发现，大量的重复随机现象构成原总体，而所有重复随机现象的结果形成数量化总体，所以数量化总体是随机现象的数量反映，研究随机现象在很大程度上就是研究数量化总体。

3.2.3数量化总体是样本数据的母体数量化总体是个体集合形式的总体，其中的个体是量化的个体，应用中样本往往是数量的形式（即样本观测值），表现为数据。所以，数量化总体是样本数据的来源，总体内个体形式和结构规定了样本中的数据形式和结构，明确数量化总体有利于数据的收集和整理。

例6：分析某地区高三学生性别与视力状况是否有关。性别和视力状况为2个分类变量，分别以X和Y代表。视力状况取“近视”和“正常”2种，则变量X和Y均为只取2个值的变量。原总体是“该地区所有在校高三学生的全体”，数量化总体中的个体形式如（x，y），如果抽测n名学生，则样本数据形如（x1，y1），（x2，y2），…，（xn，yn），这时很容易将这些数据整理成列联表。

3.3模型化总体的作用

如果说数量化总体注重变量在原总体上的实现，那么模型化总体则关注变量本身及其分布。数量化总体是量的规律的承载体，模型化总体则是统计规律的反映形式，是揭示统计规律的必要手段。

模型化总体的提出，是统计推断的首要环节。由样本推断总体，无论是推断总体分布还是推断总体中的有关参数，都是以明确总体模型为前提的。总体的分布模型确定了，随机样本中各个个体的分布才明确，在此基础上得到各类统计量的概率分布（即抽样分布），从而推断总体。所以，在数理统计学文献中，总体都是模型化总体，是随机变量或随机向量的形式。

例7：研究2个分类变量X1与X2之间的关系，模型化总体X= （X1，X2）’的概率分布：

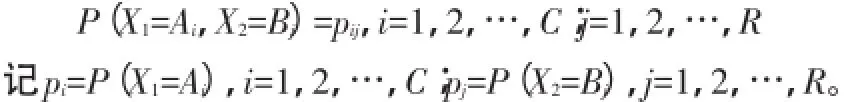
检验2个变量是否独立，即检验pij=pipj，i=1，2，…，C；j=1，2，…，R。

可见，借助模型化总体，统计推断的目标很明确。

模型化总体的提出，是统计模型的思想体现；模型化手段，是统计思想的重要体现。实际问题多种多样，统计分析常用的方法是提出模型，然后通过样本检验实际总体（数量化总体）是否符合该模型。

例8：试卷分析中，检验学生的某一门课程卷面分数是否服从正态分布。

研究目的：检查学生的考试情况是否正常（试题被默认是规范的）。原总体：参加该课程考试的所有学生。数量化总体：参加考试的所有学生卷面分数的全体。

很显然，这里的数量化总体是“有限个学生卷面分数的全体”，个体数也许只有几十个，研究目的是分析该总体中有限个学生分数的分布规律。按理说，正态分布是针对连续型随机变量的，而且正态分布随机变量的取值范围在（-∞，+∞），那么，所谓“参加考试的有限个学生卷面分数服从正态分布”如何理解呢？这正是模型化总体的作用所在，正态分布是一种分布模型，如果参加考试的有限个学生卷面分数的分布规律“符合”正态分布模型，则称该总体服从正态分布。这样，很多实际问题的总体分布就有模型可依，统计分析才会目标明确。当然，这里的学生成绩是按百分制的，随机变量的可能取值较多，而且取值范围在〔0，100〕。如果随机变量的可能取值过少，如学生成绩按5个等级计分，那么检验其是否符合某种连续型分布模型是不合适的。因为，此时随机变量的分布类型属于多项分布，勉强检验其是否服从某种连续型分布模型（如正态分布）没有实际意义。可见，模型化总体对统计方法的选用有指导作用。

4　总体的确定

总体的3种形式是因实际工作不同时段的需要而提出的，形式各异，作用互补。所以，在分析实际问题时，3种形式的总体是必须明确的。确定总体，实质上是研究目的的操作化，本身就是研究方法，也是具体研究手段的体现，涉及到具体问题，有时难度是比较大的。以下从比较宏观的层面提出确定总体时需要重点把握的3个方面。

4.1确定试验对象的共同属性

作为某一个具体问题的试验对象，必然有共同属性，这些属性是原总体的本质属性，是原总体内所有个体均具有的属性。明确了这些共同属性，也就界定了原总体的内容和范围，从而确定了原总体。

一个原总体中的个体有哪些共同属性，是由研究目的决定的。实际应用中值得注意的是，区分共同属性与研究变量的值。一个具体问题可能涉及很多变量，有些是课题需要研究的变量（称之为研究变量），有的在本课题中只取固定的值，是不变的常量，该常量构成原总体的共同属性之一。如“某一类男生的全体”，“男性”是该总体的一个共同属性，该共同属性是“性别”取固定值的结果。研究变量的值是研究变量在个体上的实现，在原总体上体现个体差异性，不能将研究变量取相同值的个体视为一个原总体。实际上，原总体的确定与研究变量的值无关，确定原总体只关心共同属性，不考虑研究变量取什么值。一个具体问题，只有一个原总体，如果出现2个或多个原总体，那么肯定是按某些研究变量取值不同而人为地分解总体，但此时已经不是在确定原总体，而是在考虑数量化总体了。之所以将原总体与研究变量分开考虑，是为了保证原总体的同质性，以便明确统计结果的适用范围，体现原总体的作用。

例9：为了探讨不同训练方法对提高100 m跑成绩的效果，将64名同年龄，身体形态和运动素质基本相同的初一男生，随机分为4组，每组16人，进行4种不同方法的训练。一学期后，按统一测量方法进行测试，得到训练前后100 m跑成绩的差值数据[13]。

这是一个单因素方差分析的例子，有2个研究变量：（1）训练方法，条件（或处理）变量，可能取4个值；（2）训练前后100 m跑成绩的差值，响应变量。研究目的：探讨不同的训练方法对提高100 m跑成绩的效果有无显著差异，即研究处理变量对响应变量有无显著影响。

原总体：训练方法适用范围内的所有男生的全体（原总体及其共性特征应当是研究者在试验前确定的，这里是笔者根据题意推测的，不一定准确）。原总体共性特征：某年龄段、一定的身体形态和运动素质、男生。

值得注意的是，原总体的确定与2个研究变量的值没有关系，不能按4种训练方法的不同，设想有4个原总体，那样容易忽视原总体的共性特征，从而模糊处理结果的适用范围。

4.2准确体现研究变量的价值信息

根据研究目的，明确了观测指标（本文称之为“研究变量”），那么原总体中的每一个个体都有观测值，所有个体观测值（即研究变量的实现值）的全体，形成数量化总体，数量化总体是原总体针对研究变量的量化结果。确定数量化总体是研究目的的操作化，必须确保所有研究变量的信息完整准确。首先，不能遗漏研究变量，尤其是作为条件变量的分类变量容易被忽视；其次，所有研究变量作为变量组必须在一个个体上同时实现。

例10：研究一个分类变量（X）对若干个响应变量（Y1，Y2，…，Ym）是否有影响。

这是单因素多元方差分析的问题。显然，分类变量和m个响应变量均为研究变量，所有研究变量用向量（X，Y1，Y2，…，Ym）’来表示。针对原总体中的每一个个体，研究变量（X，Y1，Y2，…，Ym）’有一个观测值（x，y1，y2，…，ym）’，该观测值向量是数量化总体中的一个个体，所有形如（x，y1，y2，…，ym）’的个体的集合构成数量化总体。

实际应用中，人们经常根据分类变量的取值不同，将上述数量化总体分成若干个总体。假定上述分类变量X可取3个值，针对X取某个值的所有个体构成一个总体，共有3个总体。

原总体只有一个，数量化总体之所以有多个，是因为某些研究变量已经实现，人们对相同变量值进行归类，从数量化总体中分出来。分解数量化总体，多数情况下是抽样设计的需要，为了保证样本中各类个体所占比例相对合理。

4.3随机变量及其分布模型的把握

研究变量在个体之间体现出差异性，所有研究变量均可视为随机变量，原则上，模型化总体就是所有研究变量的全体。例10中，模型化总体是随机向量（X，Y1，Y2，…，Ym）’，但在讨论随机向量的概率分布时，通常不考虑随机向量的联合分布，而是针对条件变量X的不同取值，分析响应变量（Y1，Y2，…，Ym）’关于X的条件分布。条件变量X可取3个值，有3个条件分布，所以模型化总体可视为3个，分别对应条件变量X的3个值，实质上也对应3个数量化总体。若以F1（y1，y2，…，ym），F2（y1，y2，…，ym）和F3（y1，y2，…，ym）分别表示3个总体的分布，则3个数量化总体通常也以分布F1，F2和F3来指称。

确定模型化总体的关键是总体分布模型的提出，对实际问题的有效解决往往起决定作用。在例3中，原总体是“现场执裁的6位裁判员无穷多次评分（对一个运动员）的全体”。研究变量有2个：（1）裁判员，用X表示，X可取6个值；（2）“评分结果（对一个运动员）”，用Y表示。数量化总体是“形如（x，y）的所有个体的集合”。如果按裁判员变量X取不同的值，可以将数量化总体分成6个子总体，即每一位裁判员无穷多次评分结果的全体。针对X的不同取值，考虑“评分结果”变量Y关于X的6个条件分布，得到6个模型化总体F（y|x）（x=1，2，…，6），统计模型为：

式中：μ为常数；E（εi）=0；Vαr（εi）=σi2，i=1，2，…，6，且ε1，ε2，…，ε6相互独立。

该模型在文献[11]中有详细解释。正是基于此模型，主观评分数据的处理问题得以较好地解决。

5　小　结

综上所述，原总体、数量化总体和模型化总体作为统计总体的3种形式，统一于总体这个范畴。统计总体因统计工作的需要而产生，统计学研究随机现象的规律，通过多次重复随机现象（多数情况下是人为设想的重复）来反映其内在规律，重复随机现象的过程称为（随机）试验，一次重复试验称为一个试验对象（单元），大量重复试验的集合称作总体。随机现象的规律蕴含在总体中，总体是随机现象内在规律的承载体，总体就是研究对象。总体中，陈列着所有可能的重复试验及其结果，从试验对象的角度看，总体是所有试验对象的全体（原总体）；如果关注每次试验的结果，那么总体是所有试验结果的全体（数量化总体）；透过大量的重复随机现象，看其内在规律，则总体是研究变量的概率分布（模型化总体）。

之所以从不同的视角看总体，提出3种形式，是因为实际工作的需要，3种形式的总体在统计工作的不同阶段、不同环节分别发挥不同的作用，不能互相替代。实际应用中，3种形式的总体都应该明确。从原总体到数量化总体，再到模型化总体，任何一种总体的确定不合适，都会使抽样不合理，或统计方法选用不得当，或统计分析不具有针对性，导致研究结果出现问题，且不易被发现。

各种统计方法都是针对特定总体的，而在实际工作中，总体是需要研究者自己确定的。确定总体的难度固然是有，但是对统计总体本身的深刻理解是应用者所必须的。

参考文献：

[1]耿建华.“统计总体”辨析：兼与贾俊平、周恒彤商榷[J].统计教育，2006（10）：63-64.

[2]杨绪忠.统计总体和总体单位辨析[J].统计教育，2005（4）：37-38.

[3]常乐.总体单位概念引出的歧义[J].中国统计，2001（10）：42.

[4]姜培耕.统计总体的哲学反思：兼论统计学是方法论科学[J].上海统计，2000（2）：18-20.

[5]李继梅.统计学中几个重要范畴的区别与联系[J].产业与科技论坛，2008（7）：140-141.

[6]杨昌斌.论总体与总体单位、指标与标志的关系[J].统计研究，1990 （2）：70-71.

[7]魏登云.提高体育统计应用水平的关键：正确认识统计总体[J].体育科学，1997（2）：87-91.

[8]陈希孺.概率论与数理统计[M].合肥：中国科技大学出版社，2002.

[9]贾俊平，何晓群，金进勇.统计学[M].4版.北京：中国人民大学出版社，2012.

[10]魏登云，邹可观，李良萍.记点、打分类项目裁判员个体客观性的非参数评价[J].体育科学，2006，26（9）：51-53.

[11]魏登云，李良萍.竞技体育主观评分数据的统计模型及其参数估计[J].体育科学，2008，28（7）：83-87.

[12]魏登云.主成分与因子分析在体育综合评价中的应用监测[J].体育科学，2003，23（4）：48-51.

[13]丛湖平.体育统计[M].北京：高等教育出版社，2008.

[14]张尧庭，夏立显，安希忠，等.定性资料的统计分析[M].桂林：广西师范大学出版社，1991.

[15]魏登云，杨亚莉.体育科研中定性数据的统计分析问题辨析[J].体育科学，2010，30（6）：92-96.

[16]GUDMUNDR.Iversen andM aryGerge n[M].吴喜之，程博，柳林旭，等，译.北京：高等教育出版社，2002.

[17]JOHNSONR A，WICHERN D W.实用多元统计分析[M].4版.陆璇，译.北京：清华大学出版社，2001.

中图分类号：G 80-3

文献标志码：A

文章编号：1005-0000（2015）04-345-06

DOI：10.13297/j.cnki.issn1005-0000.2015.04.014

收稿日期：2015-04-13；修回日期：2015-07-05；录用日期：2015-07-06

作者简介：魏登云（1963-），男，安徽肥东人，教授，研究方向为体育计量学。

作者单位：安徽师范大学体育学院，安徽芜湖241003

Three FormsofStatisticalPopulation and Their Position and Function in theScientific Research of Sport

WEI Dengyun，WU Jiafa
（Schoo1ofPE，AnhuiNorma1University，Wuhu 241003，China）

AbstractIn order to revea1 the nature of statistica1 popu1ation and its potentia1 in app1ication，three types of statistic popu1ation are proposed. They are primitive popu1ation，quantity popu1ation and mode1 popu1ation，respective1y. Those three types of popu1ation exhibit three different characteristics：the individua1 homoge⁃ neity in primitive popu1ation，individua1 discrepancy in quantity popu1ation，and individua1 homogenous distribution. Their ro1es and app1ications are a1so different. The primitive popu1ation is the starting point and destination of quantitative ana1ysis，which cou1d guide the statistic methods and p1ay a critica1 ro1e to statistic process resu1t. Quantity popu1ation is the operation of study goa1，carrier of quantity ru1es，and source of samp1ing data. Mode1 popu1ation ref1ects the statistic ru1es，and is an essentia1 too1 to disc1ose statistic ru1es. Severa1 aspects shou1d be paid attention to when determine which types of popu1ation：First1y figure out the common characteristics ofthestudy object.Second1y，the va1uab1e information shou1d be ref1ected precise1y.The random variab1e and its distribution mode1 shou1d be correct1y grasped.

Key wordsstatistica1 popu1ation；trai1；variab1es；probabi1ity distribution；common characteristics；individua1 differences