多桥水域航道通过能力仿真研究

徐武雄，初秀民，刘兴龙

（1.武汉理工大学水路公路交通安全控制与装备教育部工程技术中心，武汉430063；2.湖北科技学院电信学院，湖北，咸宁437100）

多桥水域航道通过能力仿真研究

徐武雄1,2，初秀民*1，刘兴龙1

（1.武汉理工大学水路公路交通安全控制与装备教育部工程技术中心，武汉430063；2.湖北科技学院电信学院，湖北，咸宁437100）

为了确定内河多桥水域的航道通过能力，提出多桥航道的交通流仿真模型.以长江武汉段的多桥航道为研究对象，收集大量的船舶交通流历史数据，用统计的方法分析这些数据获得交通流特征，提出基于蒙特卡罗方法的船舶生成模型、队列模型、航路模型和船舶运动模型等；开发仿真系统并对模型进行验证；通过仿真实验确定多桥水域的航道通过能力.仿真结果表明，所提出的内河多桥航道交通流仿真模型是可行和有效的；在目前的通航条件下，长江武汉段多桥水域的航道通过能力与实际的交通流量相比显得非常富余；在安全航速范围内，通过整体提高船舶的航行速度可以显著提高航道的通过能力；航道水深的变化对上行和下行航道通过能力的影响具有明显的差异.

水路运输；通过能力；多桥航道；建模与仿真；蒙特卡罗方法

1 引言

内河航道通过能力为航道的规划和设计及船舶交通流的管理和控制提供了重要的依据，人们通常用数学分析或仿真的方法来评估或计算航道的通过能力.比较有影响的数学分析公式是西德公式、长江公式、苏南运河公式和川江公式等[1]，这些公式均涉及到与航道和船舶等相关的很多参数，对这些参数的整定并不容易实现，另外，由于不可能用大量的实船去做试验，其计算结果的准确性很难得到有效的验证.

为了克服这些计算公式存在的缺陷，人们提出了用计算机仿真的方法来确定航道的通过能力.国外从上世纪60年代就开始了这方面的研究，O A A lmaz[2]等在Arena仿真环境下构建了Delaware河的船舶仿真模型，以便研究加深航道对运输效率和通过能力等的影响.D Mavrakis[3]等提出了Bosporus海峡的船舶交通队列模型，可实现在不同条件下的通过能力的仿真.国内从上世纪80年代才开始这方面的研究，郝世杰[4]等提出了海上交通系统GPSS仿真模拟方法，可实现对海上交通系统的定性和定量的分析.白响恩[5]等利用Arena仿真平台对港域航道的通过能力进行模拟，量化分析靠离泊作业对通过能力的影响.国外在水上交通流的仿真理论、建模方法、仿真工具和应用领域等方面的研究比国内更深入，国内外对通过能力的仿真主要集中于海上、港口和内河等航道，还未见有对内河多桥航道通过能力仿真的研究.这些仿真模型基本都以离散事件仿真软件来实现，由于这些软件的局限性，通常把船舶的尺度和速度等属性看作是不变的，且不考虑船舶之间的跟随、追越等航行行为，这必然会影响仿真结果的准确性.

长江武汉段的跨江桥梁日益增多，影响了航道的通过能力.本文提出仿真的方法对武汉市三环内的长江多桥航道的通过能力进行研究.首先对武汉市长江多桥航道的特征进行描述，对历史交通流数据进行统计分析，然后提出交通流仿真模型，并对模型进行验证，最后设计仿真实验对通过能力进行评价.

2 多桥航道特征

武汉长江航道如图1所示，自西向东架设了6座桥梁：白沙洲大桥、鹦鹉洲大桥、长江一桥、长江二桥、二七大桥和天兴洲大桥，相邻桥间距依次为：5.98 km、2.38 km、6.88 km、3.29 km和6.4 km.这段航道实行分道通航制，桥上游1 500m至下游1 000m的范围被称之为“桥区”，在桥区船舶禁止追越和并列行驶.图1中曲线C1A1C2…C7A6C8及D1B1D2…D7B6D8构成仿真航道的边界.根据“桥区”的定义，将多桥航道划分为“禁止追越区”和“允许追越区”.“禁止追越区”：C1D1－C2D2是桥梁A1B1的“禁止追越区”；由于桥梁A2B2和A3B3的距离太短，故这两座桥梁的“禁止追越区”是连续的，位于C3D3－C4D4之间；同样，桥梁A4B4和A5B5的“禁止追越区”位于C5D5－C6D6之间；C7D7－C8D8是桥梁A6B6的“禁止追越区”.“允许追越区”为：C2D2－C3D3，C4D4－C5D5和C6D6－C7D7.

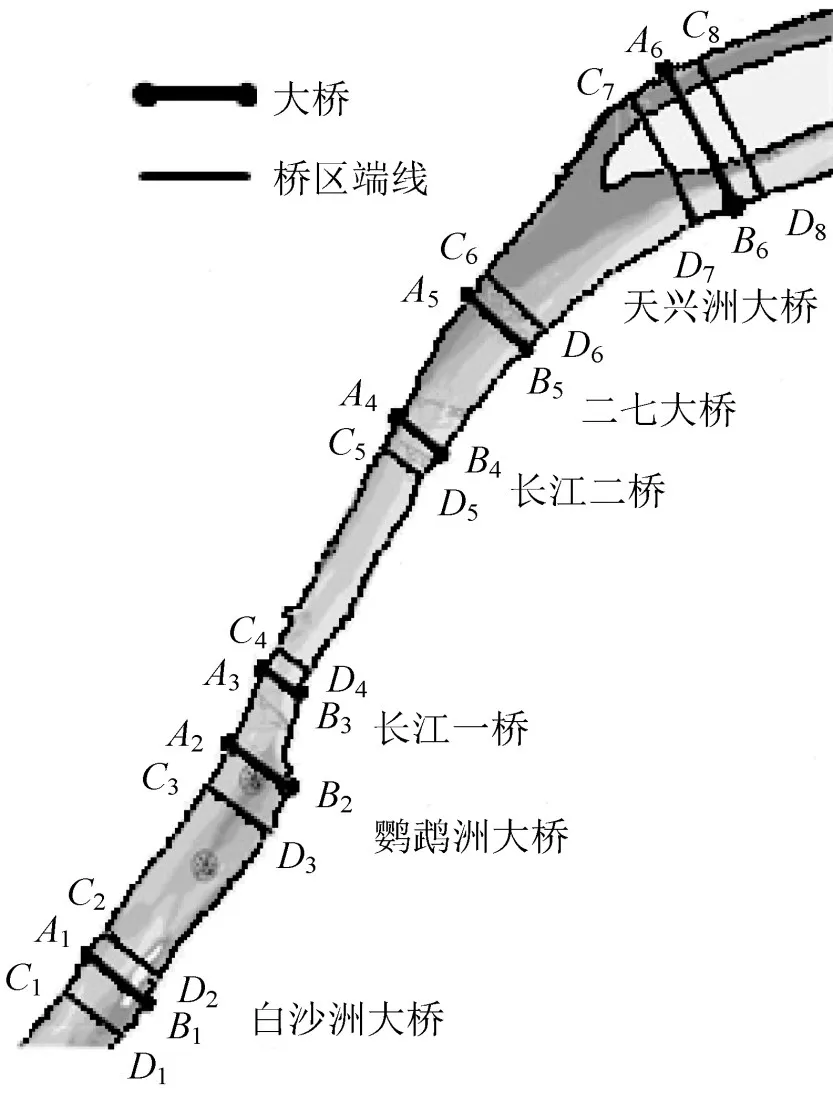
图1 武汉长江航道Fig.1 Waterway of the Yangtze River inWuhan

3 数据来源

收集交通流历史数据是用蒙特卡罗方法仿真交通流的基础和关键.历史数据通过以下方式获取：

（1）AIS（Automatic Identification System）数据.

课题组在白沙洲大桥、长江一桥和天兴洲大桥各安装了1台AIS接收机，每天不间断接收过往船舶发送的AIS信息.

（2）断面统计数据.

长江海事局每月定期对通过长江一桥断面的船舶交通流量进行统计，统计船舶的种类、数量、长度等信息，课题组获取了2009–2012年的这些数据.

4 船舶交通流特征

4.1 船舶数量和类型

对通过长江一桥断面的船舶交通流量进行统计，2009–2012年每月的日平均流量如图2所示，其日平均流量保持在400艘左右.船舶类型的分布如表1所示.

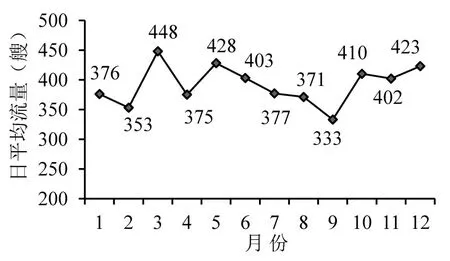
图2 2009–2012年每月的日平均流量Fig.2 Daily permonth average flow for2009–2012

表1 船舶类型比例Table 1 Percentofvessel types

4.2 船舶尺寸

航道船舶的尺寸不仅跟船型有关，也随航道水深的增加而增大.武汉桥区航道通常每年的11月–次年3月为枯水期，维护水深平均为4m；4月、5月和10月为中水期，维护水深为5m；6月–9月为洪水期，维护水深为6m.

对上行和下行货船长度数据进行统计分析发现，二者均符合正态分布，概率密度函数如式(1)所示.其参数估计值在枯水期、中水期、洪水期依次为

对于上行和下行的危险品船、集装箱船、船队和其它船舶，其长度数据也符合正态分布，对应的参数估计值在枯水期依次为μ̂=63、98、123和48，σ̂=15、16、24和20；中水期为μ̂=68、100、125和50,σ̂=17、14、29和22；洪水期为μ̂=71、102、126和51,σ̂=20、13、25和18.

4.3 船舶到达规律分布

如图1所示，C1D1和C8D8分别为下行和上行船舶的起始门线.以小时为单位时间，统计船舶在单位时间内到达门线的次数，统计时长为24 h.以2012年1月–12月AIS数据作为数据源，取每月中最接近日平均流量的那天的数据为样本.经分析发现船舶到达这两条门线的规律符合Possion分布，如式（2）所示.

由于每月船舶的平均流量不同，分布参数λ也有所差异.比如，2012年3月（枯水期）的日平均流量为上行202艘，下行218艘，其对应的λ值分别为：8.2和9.5，用一维数组表示为λ0=[8.2,9.5].5月（中水期）和7月（洪水期）的λ分别为λ1=[7.9,8.3]，λ2=[7.6,8.0].

4.4 船舶速度

船舶的速度（对地速度，km/h）跟船型、流速和桥区的航行规则等因素有关.在枯水期、中水期和洪水期，船舶的下行速度通常依次增加，上行速度依次减少.仿真时，船舶速度采用平均速度.经统计，在枯水期，货船、集装箱船、危险品船、船队和其它船舶的上行平均速度依次为：6.89、7.86、7.75、7.10和7.09，下行依次为：11.8、12.86、15.48、14.26和11.2，这些速度用二维数组V0表示：V0=[6.89, 7.86,7.75,7.10,7.09；11.8,12.86,15.48,14.26, 11.2].中水期和洪水期速度分别用V1和V2表示：V1=[6.19,7.25,7.11,6.60,6.58；13.1,13.87,16.35, 15.18,12.4]，V2=[5.56,6.82,6.65,6.16,6.13；13.9, 14.77,17.05,15.99,13.2].

5 交通流仿真模型

5.1 船舶生成模型

船舶的生成采用蒙特卡罗方法，根据第4节所述的船舶交通流的统计分布规律，形成随机变量生成算法，在仿真时，先产生船舶到达时间间隔随机变量，并转化成船舶到达的时间，当仿真时间步进到这个船舶到达的时间时则产生一条船舶，并生成船舶的属性.

5.2 队列模型

航行时，后船与前船需保持最小安全距离，用SDmin表示，根据船舶领域的定义及文献[6]的研究结果，可确定下行船舶的SDmin=(4LA+4LB)/2，上行船舶的SDmin=(3LA+3LB)/2，其中，LA和LB分别表示前船和后船的船长.如果生成的船舶与最后进人航道的船舶之间的距离小于SDmin，则该船不能进人航道，需进人队列排队等待.

5.3 船舶路径模型

船舶的路径示意图如图3所示.图中字符A1,…,A6；B1,…,B6；C1,…,C8；D1,…,D8与图1中对应的字符含义相同.虚线S1S2S3…S12S13S14是由航标标示的航道分隔线.船舶的路径采用OD (Origin and Destination)交通流模型[7]，图中带数字的圆圈表示节点，序号最小的节点表示起点，最大的表示终点，节点之间的直线段表示路径，箭头表示航向.分隔线右边的节点1，2，…，14依次相连构成了下行路径，左边的节点1，2，…，14依次相连构成了上行路径.

节点位置的确定方法如下.如图4所示为船舶在下行航道门线S1D1上的位置分布的直方图和拟合曲线，坐标原点为S1点，X轴为船舶位置到S1的距离.从图4可知，拟合曲线为正态分布的概率密度函数，其参数估计值μ̂=87.59，δ̂=38.72.对下行航道其它门线上的位置分布也服从相同的正态分布，只是其2个分布参数的估计值有所不同，这样选择参数μ̂所在的位置坐标作为节点位置.对于上行节点位置可以采用同样的方法确定.

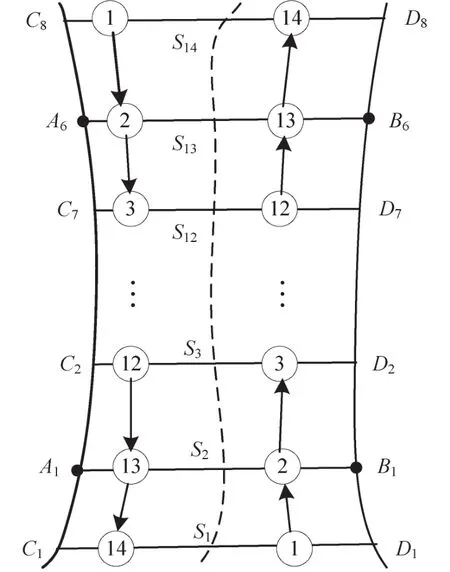
图3 船舶路径模型Fig.3 Routemodelofvessels

图4 门线上船舶位置分布Fig.4 Position distribution ofvesselsacrossa gate line

5.4 船舶运动模型

基于这段水域的通航规则，船舶有3种运动模式：自由航行、跟随和追越，后船跟随前船运动时，2船之间需保持最小安全距离SDmin.

自由航行.当后船与前船的距离大于SDmin时，后船沿着OD路径以自己的速度航行，在节点处改变航向.

跟随运动.在禁止追越区，后船不允许追越前船，只能跟随前船航行，后船与前船需要保持最小安全距离SDmin.如果后船的速度不大于前船的速度时，两船的间距不会减小，两船没有碰撞危险，则两船的速度都不需要调整；如果后船的速度大于前船时，两船的间距会逐渐减小，当减小到SDmin时，则需调整后船的速度，使其速度等于前船的速度.

追越运动.在允许追越区，如果后船的速度小于或等于前船的速度，说明后船没有追越意图，则后船保持速度不变，做自由航行；如果后船速度大于前船速度，说明后船有追越意图，则采取追越行动.追越路径如图5所示，A船为被追越船，B船为追越船，实线为既定路径，虚线为追越路径，追越时，A船保持原来的速度沿着既定路线航行，B船改变路径沿着追越路径航行，图5（a）为上行船舶的追越路径模型，由于上行船舶的OD路径偏向上行航道的右侧，其追越路径位于上行航道的左侧，图5（b）为下行船舶的追越路径模型，由于下行船舶的OD路径偏向下行航道的左侧，其追越路径位于下行航道的右侧.在图5（b）中，t1时刻，当A船和B船纵向间距小于或等于SDmin时，则B船开始转向，转向角度向右偏转15度，当B船航行到t2时刻，B船与OD路径的横向距离等于50m时，B船再次转向，向左偏转15度，航向与OD路径平行，当B船航行到t3时刻，B船与A船的纵向距离等于安全距离时，B船再次转向，向左偏转15度，当B船航行到t4时刻，B船回到了OD路径上，B船再次转向，向右偏转15度，沿OD路径航行，追越过程完成.在追越过程中，t1-t2，t3-t4这段时间B船的速度保持为追越前的速度，t3-t4这段时间B船的速度调整为它的最大速度，经统计，下行船舶的最大速度为18 km/h，上行的最大速度为11 km/h.

6 模型验证

基于上述模型的仿真系统在Visual Studio 2008开发平台上实现，使用C++语言编制算法程序，利用SQL Server 2008对生成的仿真船舶数据进行管理.将仿真生成的船舶交通流与2012年3月的实际船舶交通流进行比较，对仿真模型进行验证.

仿真系统所需的船舶交通流特征和交通流模型均是对武汉桥区实际的交通流数据进行统计和分析所得，反映实际的交通状态.同时假设航道的水深、流速、风浪和能见度等水文气象条件良好，不影响船舶的正常航行，且船舶均遵守桥区的航行规则.

图5 追越路径模型Fig.5 Overtaking routemodel

本次实验称之为“实验1”，仿真参数设置如下：

船舶的类型分布规律采用表1；船舶的长度分布采用式（1），取枯水期对应的参数值；船舶的到达规律分布采用式（2），上行和下行的Possion分布参数取λ0；船舶速度采用V0；仿真时间步长取10 s；仿真预热时间4.5 h，仿真时长1 d（24 h）.仿真运行30次，运行结束后统计通过长江一桥断面的船舶交通流量，并用平均值与实际值进行比较，如表2所示.比较结果表明，仿真船舶与实际船舶的数量是比较接近的，其相对误差都小于10%，说明仿真模型能以较高的精度模拟实际的交通状况.

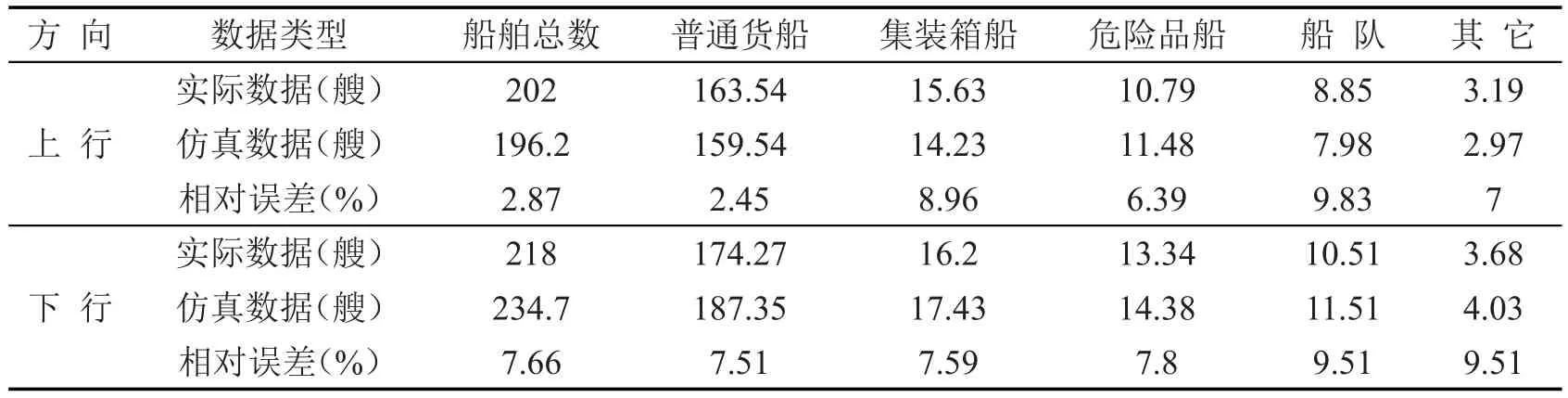
表2 仿真数据与历史数据的比较Table 2 Comparing simulation data with historicaldata

7 通过能力仿真

7.1 通过能力仿真方法

保持实验1的其它仿真参数不变，调整船舶到达的时间间隔，即调整分布参数λ的大小，随着λ的增加，通过一桥断面的船舶数量会逐渐增加，当通过的数量不再明显增加时，说明通过桥区的船舶数量已到达饱和，这时通过的数量被看作通过能力.

以实验1中的λ0为基础，上行和下行λ值取6组：针对这6组不同的λ值，依次进行仿真，结果如图6所示.

图6 不同lambda时通过的船舶数量Fig.6 Vesselnumberof transitunder different lambdas

从图6可以看出，通过断面的上行和下行船舶的数量随λ逐渐增加，最后趋于饱和，基本维持一个不变的数量，这个数量可确定为断面的通过能力.可以看出，上行和下行的通过能力分别为547艘和885艘左右.在目前的通航条件和船舶属性下，通过武汉桥区的双向船舶日通过能力大约为1 400艘，实际日通过的船舶数量大约为400艘，说明武汉桥区的通过能力是非常富余的，反映了长江中游的水路运输资源的利用率还比较低，没有充分发挥水路运输资源的优势.

7.2 不同速度下的通过能力

从图6可知，上行和下行的通过能力差异比较大，主要是由于上行和下行船舶的速度差异导致的.保持7.1节实验其他条件不变，船舶的速度V0依次增加1 km、2 km和3 km，即，依次做速度为时的仿真，结果如图7所示，在安全速度的范围内，通过能力随着速度的增加而增大.目前通过武汉桥区的船舶速度是比较低的，远低于船舶的额定速度，通过整体提高船舶的航行速度也可以显著提高船舶的通过能力.

图7 不同速度时的通过能力Fig.7 Transitcapacity under differentvelocities

7.3 航道水深变化时的通过能力

武汉桥区航道水深在枯水期、中水期和洪水期逐渐增加，使更大尺寸的来船数量相应增加，对应提高了船舶长度概率分布的均值μ，进而影响航道的通过能力.在这三种时期不同μ值的条件下进行仿真，可以在一定程度上反映航道水深变化对通过能力的影响.由于水深的变化伴随着流速的变化，流速的增加使下行的船速增加，上行的船速减少，因此仿真时要考虑流速的影响.以7.1节实验为基础，分别做这三种时期的通过能力仿真实验，设置仿真参数：长度分布均值μ依次取4.2节所述的三种时期对应的值；船舶到达规律依次取λ0、λ1和λ2；船舶速度依次取V0、V1和V2.由于这三种长度均值μ是不同的，生成的船舶数量不能正确反映通过能力的变化，需进行当量化，转化成标准船，船长L（m），长江内河的当量系数为

结果如图8所示，标准船的数量对应航道的通过能力，对于下行航道，仿真船和标准船的数量随着航道水深的增加有明显的增长，对于上行航道，由于逆水航行的船舶速度减小，随着航道水深的增加，仿真船舶的数量减少，但由于大船数量的增加，标准船舶的数量略有增加，这说明航道水深的变化对上行和下行航道通过能力的影响具有明显的差异，航道水深增加时，要提高上行航道的通过能力必须提高船舶的速度.

图8 不同航道水深的通过能力Fig.8 Transitcapacity underdifferentwaterway depth

8 研究结论

以长江武汉段多桥航道为研究对象，提出了一种内河多桥航道交通流仿真模型，通过设计仿真实验，实现了对这一特殊航道通过能力的评价.经验证，仿真模型能以较高的精度模拟实际的交通状况.通过能力仿真结果表明：在目前的通航条件下，武汉多桥航道的通过能力与实际的交通流量相比显得非常富余；在安全航速范围内，通过整体提高船舶的航行速度可以显著提高航道的通过能力；航道水深的变化对上行和下行航道通过能力的影响具有明显的差异；仿真系统通过设置不同的仿真参数，可以实现在不同通航环境和交通流特征下的通过能力仿真，仿真模型稍作修改也可以应用到其它桥区航道.

[1]初秀民，李祎承，余玉欢.长江中下游航道通过能力计算方法[J].交通运输系统工程与信息，2014,14(2)：213-219.[CHU X M,LIY C,YU Y H.Calculation method for traffic capacity in the midstreamdownstream of Yangtze River[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(2)：213-219.]

[2]Almaz O A,Altiok T.Simulation modeling of the vessel traffic in Delaware River:Impact of deepening on port performance[J].Simulation Modellig Practice and Theory.2012,22:146-165.

[3]Mavrakis D,Kontinakis N.A queuingmodel ofmaritime traffic in bosporus straits[J].Simulation Modelling Practice and Theory,2008,16:315-328.

[4]郝世杰，杨守仁，方祥麟.海上交通系统GPSS模拟及应用[J].大连海运学院学报，1986，12（4）：1-11. [HAO SJ,YANGSR,FANG X L.Marine traffic system GPSS simulation and application[J].Journal of Dalian Marine College 1986，12（4）：1－11.]

[5]白响恩，周伟，郑剑,等.基于离散事件的港域航道通过能力仿真试验[J].水运工程，2014，（6）：118-122. [BAI X E,ZHOU W,ZHENG J,et al.Discrete event simulation on traffic capacity of harbor channel[J].Port &Waterway Engineering,2014（6）：118-122.]

[6]侯海强，李祎承，初秀民.长江繁忙水域船舶间距模型[J].大连海事大学学报，2013，39（4）：21-24. [HOU H Q,LIY C,CHU X M.Vessel clearancemodel in busy waters of the Yangtze River[J].Journal of Dalian Maritime University,2013，39（4）：21-24.]

[7]吴发林，方祥麟.基于OD船舶交通模拟的研究[J].大连海事大学学报，1998，24(4):10-13.[WU F L,FANG X L.Maritime traffic simulation based on OD[J].Journal ofDalian Maritime University,1998，24(4)：10-13.]

Simulation for Transit Capacity of a Multi-bridge Waterway

XUWu-xiong1,2,CHU Xiu-m in1,LIU Xing-long1

(1.Engineering Research Centerof Transportation Safety,Wuhan University of Technology,Wuhan 430063,China;2.The Schoolof Electronic and Information Engineering,HubeiUniversity of Science and Technology,Xianning 437100,Hubei, China)

Simulation models of vessel traffic flow in amulti-bridge waterway are proposed in order to determ ine transit capacity of the waterway.The multi-bridge waterway belonging to the Yangtze River in Wuhan is as the research case.Firstly,a large number of historical data aboutvessel traffic flow are collected and the data are analyzed using statistical methods to obtain traffic flow characteristic;secondly,the simulation models are present involving a vessel generating model based on the Monte Carlo method,a queuemodel,a routemodel and a vesselmovementmodel;thirdly,the simulation system is developed and themodelsare validated;finally,the transitcapacity of thewaterway is determ ined by simulation.The results show that the proposed simulation models are feasible and effective,under the present navigational conditions the transit capacity of thewaterway ismuch greater than the actual vessel traffic flow;in the safe speed range the transit capacity can significantly be improved if vessel velocitiesare increased and the effect ofwaterway depthson upbound and downbound vessels iswith obviousdifference.

waterway transportation;transit capacity;multi-bridge waterway;modeling and simulation; Monte Carlomethod

1009-6744（2015）03-0127-07

U675;TP391

A

2014-12-15

2015-03-19录用日期：2015-03-25

国家自然科学基金项目（61273234，51479155）；湖北省自然科学基金创新群体项目（2013CFA007）；交通运输部信息化技术研究项目（2013-364-548-200）.

徐武雄（1971-），男，湖北通城人，博士生.＊通信作者：chuxm@whut.edu.cn