物理层网络编码的符号时钟估计
党小宇 李 强 虞湘宾 王旭东
(南京航空航天大学电子信息工程学院 南京 210016)
物理层网络编码的符号时钟估计
党小宇 李 强*虞湘宾 王旭东
(南京航空航天大学电子信息工程学院 南京 210016)
现有的关于物理层网络编码(PNC)的研究多建立在时钟已完全同步的基础上,对PNC的符号时钟同步研究较少。而实际上符号时钟在PNC中是必不可少的。针对这一问题,该文提出一种新的基于正交训练序列适用于双向中继信道PNC的符号时钟估计方法。该方法根据最大似然估计准则,运用基于离散傅里叶变换(DFT)的插值算法来估计时钟误差。仿真结果表明,所提出的DFT插值算法性能优越,在信噪比(SNR)大于10 dB的条件下,系统的均方误差(MSE)性能比经典优选采样点法提升1个数量级,并且非常逼近修正克拉美罗界(MCRB)。
无线通信;物理层网络编码;双向中继信道;符号时钟估计;修正克拉美罗界
1 引言
物理层网络编码(Physical-layer Network Coding,PNC)[1,2]的概念在2006年首次提出后,就迅速引起了通信界的广泛关注,并成为现代通信研究的热点。它不同于大多数传统的通信系统将非目标信源发出的信号视为干扰加以抑制,而是利用电磁波在传播空间内的自然叠加,中继端根据接收的叠加信号,按照一定规则在物理层编码,再将编码信息发送,而终端根据解码规则来获得传输的信息,使得干扰变成网络编码中算法操作的一部分。它能极大地提高系统的吞吐量,例如,在双向中继信道中,相比传统的未采用网络编码的系统,吞吐量提升100%。
类似于其他通信系统,符号时钟在PNC中也是必不可少的。目前已有的关于 PNC的理论研究结果,比如基于连续相位频移键控和正交振幅调制的PNC[3,4],PNC中继策略及中断性能研究[5]、多输入多输出PNC(Multiple Input Multiple Output PNC,MIMO PNC)[6,7]和多路PNC(Multi-Way PNC)[8,9],多建立在符号时钟已完全同步的基础上。虽然可以通过单输入单输出(Single Input Single Output,SISO)的方法[10,11],即分别单独估计每个端节点到中继节点之间的延时,但是这样占用了大量通信资源,且同步时间长,不适用于移动通信等信道变化快的场合。
更进一步,文献[12]提到了PNC的符号时钟同步问题,并指出对于BPSK调制,符号时间同步误差或载波相位误差会产生严重的误比特率性能损失,而如果不能有效估计时钟,会直接导致PNC通信失败。文献[13]针对PNC符号时钟异步问题,利用置信传播(Belief Propagation,BP)算法,可降低误比特率性能损失。但这是以大幅度提高系统复杂度和降低系统的信息传输效率为代价的。
本文研究双向中继信道下 PNC的符号时钟同步问题。与以往建立在时钟已同步基础上的研究不同,本文假定两个终端信号的符号时钟不同并且是未知待估的。在这更为实际的情况下,提供了一种新的基于正交训练序列的时间同步解决方法,其核心是运用最大似然估计准则和相应的基于离散傅里叶变换(Discrete Fourier Transformation,DFT)的插值方法来估计端节点的符号时钟误差。仿真结果表明,所提出的DFT插值算法性能优越,在32位的训练序列长度、4倍过采样率及18 dB的信噪比(Signal-to-Noise Ratio,SNR)条件下,均方误差(Mean Square Error,MSE)能达10-4。在SNR大于10 dB时,其MSE性能比经典优选采样点算法提升至少1个数量级,而且非常逼近MCRB。
本文内容安排如下:第2部分给出问题阐述;第3部分提出基于DFT插值的时钟误差估计算法;第4部分给出仿真结果与讨论;第5部分总结全文。
2 问题阐述
双向中继信道的PNC模型是3个节点的线性网络,其中两个端节点,节点N1和节点N2通过中继节点R实现通信,它们之间因没有直接信号通路而不能直接通信,且3个节点都假设为半双工工作模式。系统模型如图1所示。
在时隙1,节点N1,节点N2同时发送信号至中继节点R,因为异步,则节点R上的接收信号表示为
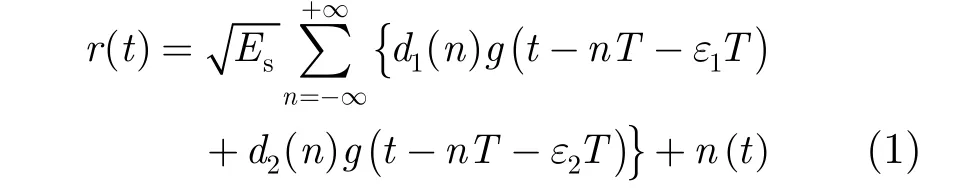
式中,sE为符号能量;1()d n和2()d n分别为从节点N1和节点N2发送的信息序列;()g t为发送滤波器,T为符号周期; ()n t为节点R上的复值循环高斯白噪声,其功率谱密度为分别为节点N1,节点N2的符号时钟误差,且 ε1≠ ε2。
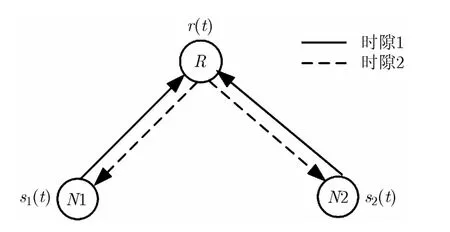
图1 物理层网络编码结构图
在时隙2,中继节点R将物理层网络编码后的信息广播给节点N1和节点N2,然后节点N1和节点 N2通过译码获得对方信息,从而实现两节点之间的通信。
在中继R,对接收信号 ()r t以Q倍的符号率1/T采样,经匹配滤波后得
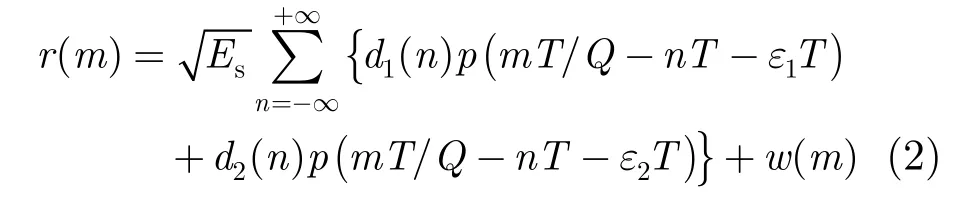
需要说明的是:
(1)12,ε ε在中继节点存在节点模糊问题。即中继节点虽然能通过估计得到两个时钟误差,但是若没有额外信息,中继节点不能区分1ε对应节点 N1还是节点N2,同样地,它也不能区分2ε对应节点N1还是节点N2。
(2)针对上述节点模糊问题,一种可行的解决办法是,中继将两个时钟误差估计值之差 ε1- ε2广播给两个端节点,然后每个端节点根据该差值调整自己的时钟,使两个端节点发送的信号在同一时刻到达中继节点。
为了获得时间同步,正交训练序列可以周期性地在数据码元间发送。本文采用恒包络零自相关(Constant Amplitude Zero Autocorrelation Waveform,CAZAC)序列[14]。为了消除信息数据和正交训练序列之间的码间串扰,在训练序列的前端和末端添加长度为N的循环前缀和循环后缀,如图2所示。图中为从第序列。
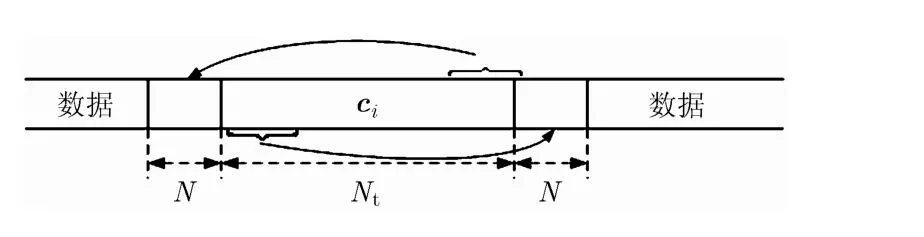
图2 节点N1,节点N2上的训练序列结构

3 符号时钟估计
为简化接收信号的表示,将相同相位的采样点组成向量 ()kr
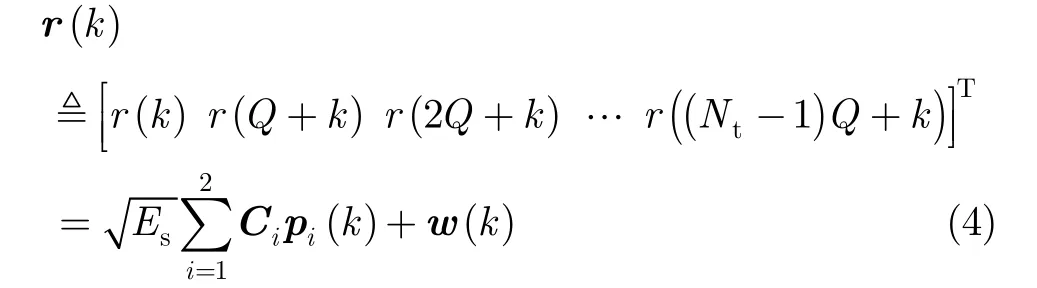
式中
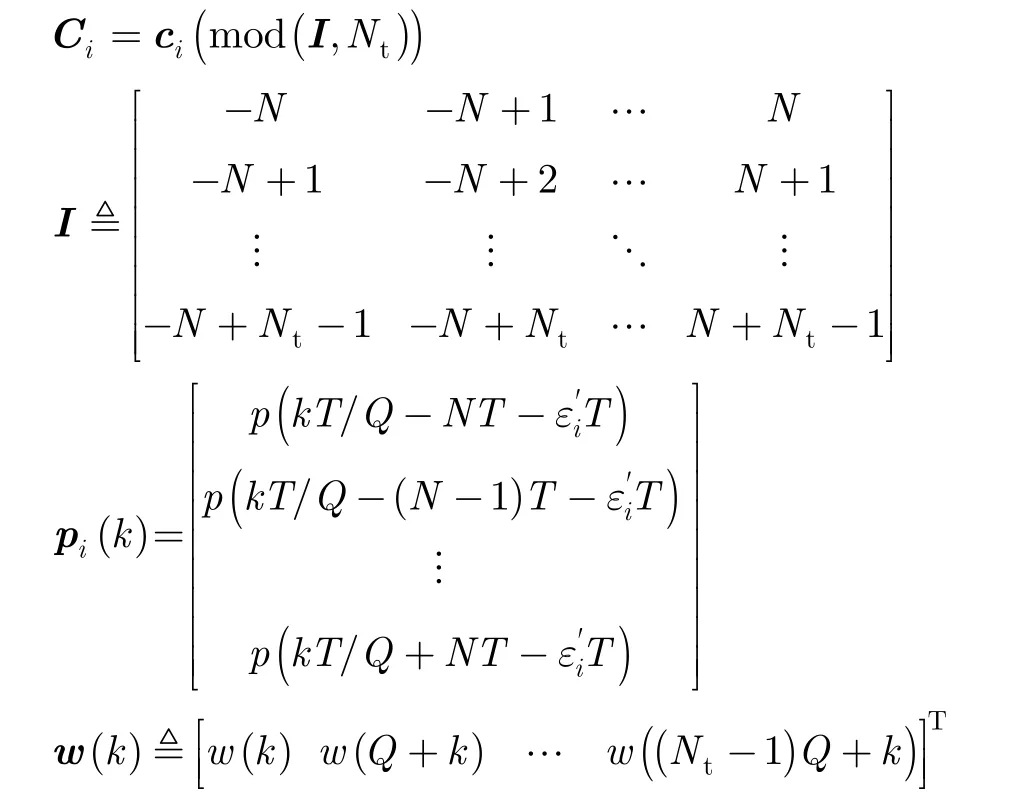
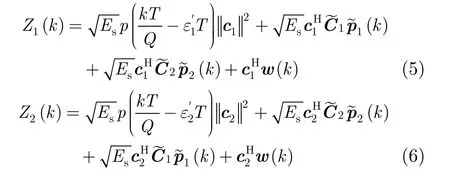
因为正交训练序列满足
所以有
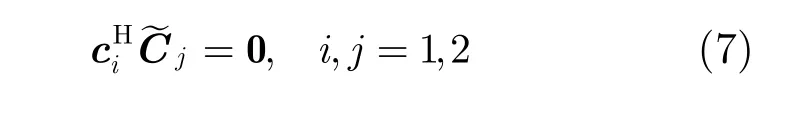
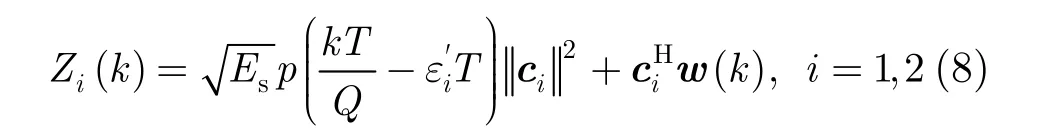
根据最大似然估计准则[15],估计的似然函数可表达为
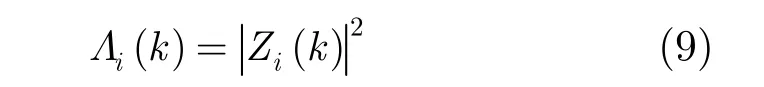
因此,时钟误差估计问题表述为
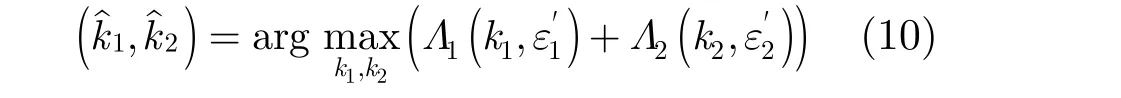
(1)优选采样点法 一种简单的符号时钟同步方法就是选取最靠近最佳采样时刻的 1 2,k作为的估计。由于 ε1,ε2独立,并且 Λi(k)只包含 εi的信息,所以有
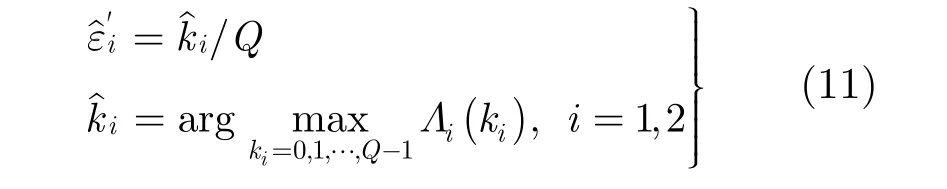
这里称式(11)为优选采样点法。由于该算法与过采样率Q密切相关,为了获得较小的MSE,需要采用相对较高的过采样率。这就对电路设计提出了更高要求并且增加了实现成本。
(2)多项式插值法 为了提高估计精度同时降插来近似获得其对应的连续似然函数。寻找该连续似然函数的最大值,就可以得到符号时钟误差的估计值。这样使得在过采样率Q较小的情况下,仍能获得较高的估计精度。
一种方法是通过 1Q- 次多项式来近似连续似然函数,即
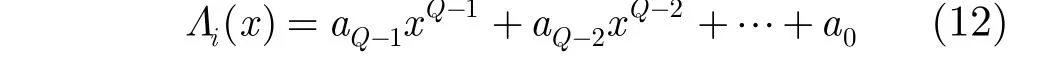
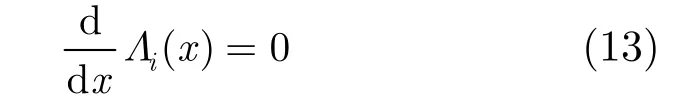
当然也可以采用其他插值方法如由分段三次多项式组成的三次样条插值,但是该方法需确定多个三次多项式,计算量较大。
(3)基于DFT的插值法 为了进一步提高估计精度,降低计算复杂度,下面提出一种基于DFT的插值算法来估计时钟误差,我们将看到该算法的计算量很低。
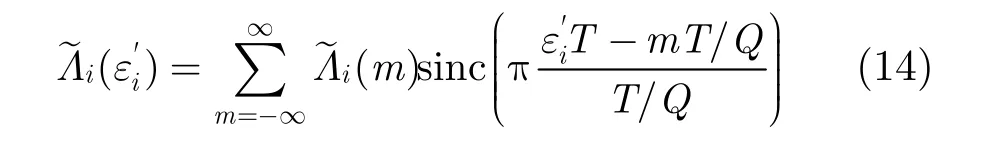
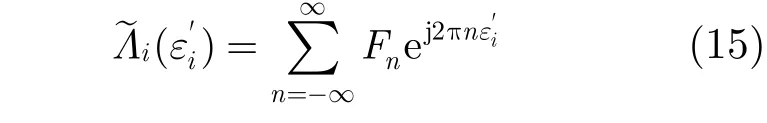
式中,
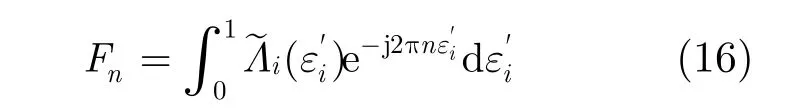
将式(14)代入式(16)中,经过一系列计算可得Fn。通过计算可发现 F±1远大于 Fn(n > 1),所以式(15)可简化为

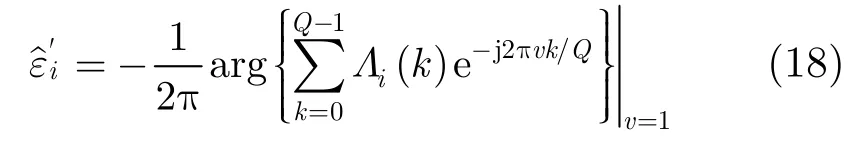
式中,arg{}x表示x的相位。式(18)中取相位运算的实际上是 Λi(k )Q点DFT的第2个输出,并且当Q= 4时,只需要若干个加法器就可以实现。
最后,根据算法所需的实数乘法(除法)和实数加法(减法)次数来比较 3种方法的计算复杂度。计算对于每一个k需 Nt+ 1次复数乘法和t1N- 次复数加法。因为 1次复数乘法需 4次实数乘法和2次实数加法,1次复数加法需2次实数加法,所以为了获得似然函数 Λi(k )共需 (4Nt+ 4)Q 次实数乘法, 4NtQ实数加法。3种方法的计算复杂度比较结果如表1所示。对于多项式插值法,采用经典的克莱姆法则计算式(12)中的多项式系数。对于基于DFT的插值法,采用快速傅里叶变换计算式(18)中的 DFT,取相位运算采用近似arctan(x )= x- x3/3 + x5/5 - x7/7获得。表2给出了3种方法在 Nt= 32,不同Q值下所需实数乘法次数的具体数值。

表1 3种方法的计算复杂度比较
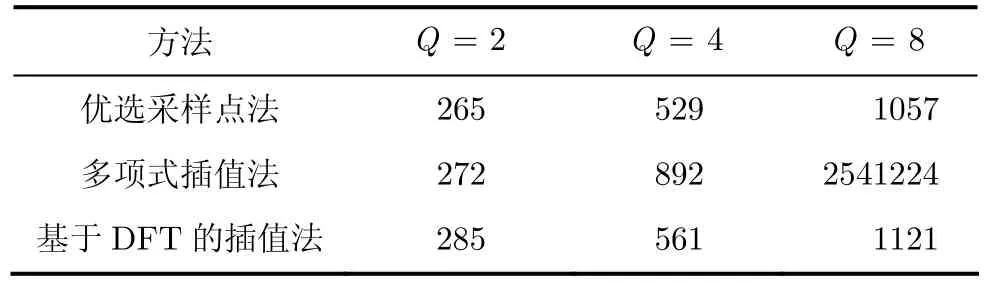
表2 Nt32= ,不同Q值下所需实数乘法次数比较
通过对比发现,优选采样点法的复杂度最低,基于DFT的插值法其次,而多项式插值法复杂度最高;基于DFT的插值法的算法复杂度比优选采样点法仅增加了约10%,但在后面的仿真中可以看到,其性能将大幅度提高。
此外,为了评估算法性能,引入MCRB[16]作为其衡量标准,
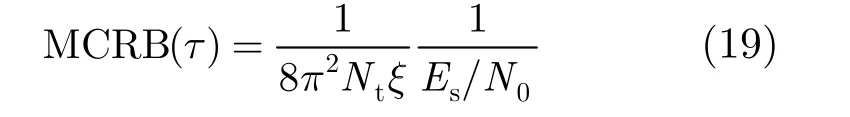
4 仿真结果与讨论
下面通过Monte-Carlo仿真来评估本文所提出算法的MSE性能。在所有仿真中,εi在(- 0.5,0.5)内均匀分布, p( t)为升余弦脉冲,训练序列 ci为
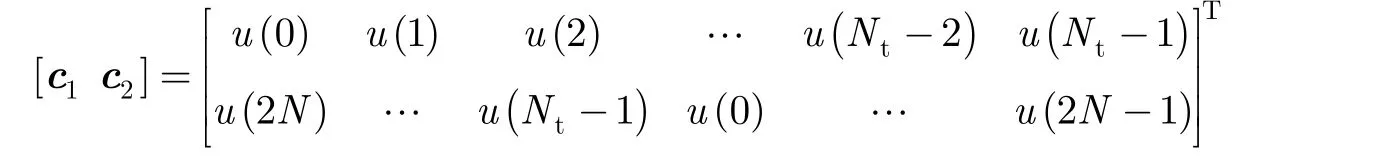
仿真 1 为了比较各种算法的性能,本文仿真了优选采样点法,三次多项式插值法和基于DFT的插值法 3种算法的 MSE。仿真中过采样率 4Q= , p( t)滚降系数 α= 0.3。
图 3和图 4分别比较了在训练序列长度tN= 32和 Nt= 64下,3种不同算法的MSE与SNR的关系。从图3和图4可以看出,3种算法的MSE都随着 SNR的增大而减小。但优选采样点算法的MSE,在SNR=10 dB处就达到下界,不随SNR的增加而减小。对于该算法,即使在最为乐观的情况下,选取的采样点最靠近最佳采样时刻,估计误差也是均匀分布在[1/(-2),Q1/(2Q) ]的随机变量,MSE存在下界21/(12 )Q 。
而对于多项式插值法和基于DFT的插值法,因其通过内插近似获得连续似然函数,它能提供比离散似然函数更精确的信息,所以两者的性能都比优选采样点算法更好。而且基于DFT的插值算法因其在插值过程中损失有用信息较少,性能优于多项式差值法。同时从图中可以看出,基于DFT的插值算法在低、中SNR区域内非常接近MCRB。
仿真2 从仿真1可知,在相同的仿真参数下,基于DFT的插值算法比优选采样点算法性能更好。为了进一步了解该算法在不同参数下的性能,本文分别仿真该算法在不同过采样率,不同训练序列长度和不同滚降系数下的MSE性能。
图6给出了基于DFT的插值算法在不同训练序列长度下的MSE性能。由图可见,低信噪比下的性能随着训练序列长度的增加而迅速提升。MSE在 10-4附近时,训练序列长度增加1倍,大约能获得2 dB的性能增益。但是在高信噪比端,所有tN的 MSE都收敛于 3 × 10-5。
图7显示了算法在不同滚降系数下的MSE性能。从图中可以看出,MSE随着SNR的增大而减小,并且性能随着滚降系数的增大而提升。MSE在 10-4附近时,滚降系数 α= 1相比 α= 0大约能获得2 dB的增益。
5 结束语
针对 PNC的双向中继信道下的符号时钟同步问题,本文假定两个端节点之间存在相对时钟快慢,两个终端信号在不同时刻到达中继节点。在这更为实际的前提下,根据最大似然准则,提出了一种新的基于DFT插值的符号时钟误差估计算法。数值仿真表明,所提出的DFT插值算法性能优越,在32位的训练序列长度、4倍过采样率及18 dB的信噪比条件下,MSE能达 10-4。在信噪比大于10 dB时,其MSE性能比经典优选采样点算法提升1个数量级,而且非常逼近MCRB。
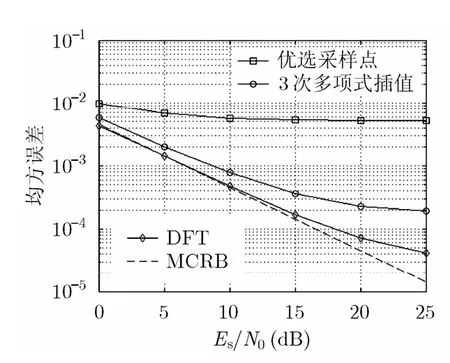
图3 不同算法的MSE性能比较
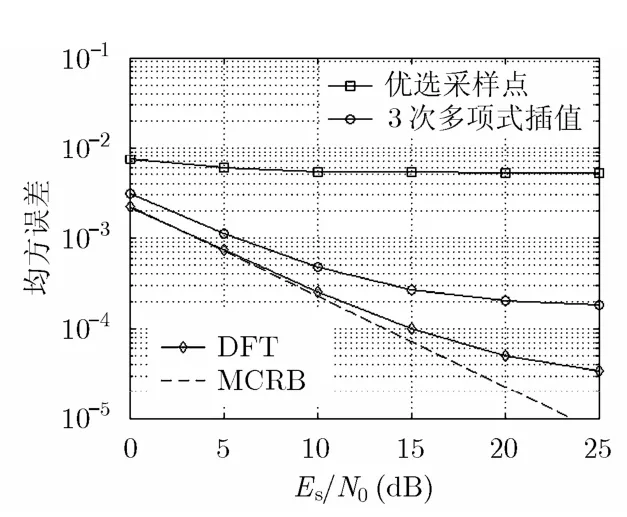
图4 不同算法的MSE性能比较
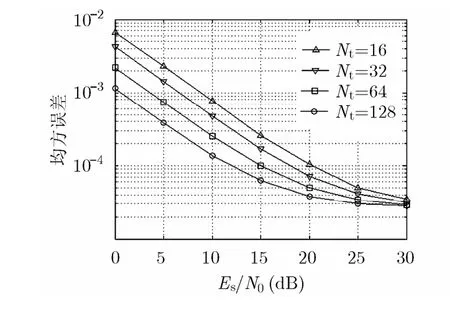
图6 不同训练序列长度的MSE性能

图7 不同滚降系数α的MSE性能
[1] Zhang S,Liew S C,and Lam P P. Hot topic:physical-layer network coding[C]. Proceedings of the 12th Annual International Conference on Mobile Computing and Networking,CA,USA,2006:358-365.
[2] Liew S C,Zhang S,and Lu L. Physical-layer network coding:tutorial,survey,and beyond[J]. Physical Communication,2013,6:4-42.
[3] 沙楠,高媛媛,益晓新,等. 基于连续相位频移键控调制的物理层网络编码检测及性能分析[J]. 电子与信息学报,2014,36(6):1454-1459.
Sha Nan,Gao Yuan-yuan,Yi Xiao-xin,et al.. Physical-layer network coding based on CPFSK modulation detection and performance analysis[J]. Journal of Electronics & Information Technology,2014,36(6):1454-1459.
[4] Namboodiri V,Venugopal K,and Rajan B S. Physical layer network coding for two-way relaying with QAM[J]. IEEE Transactions on Wireless Communications,2013,12(10):5074-5086.
[5] 吉晓东,郑宝玉. 物理层网络编码机会中继及中断性能分析[J]. 电子与信息学报,2011,33(5):1186-1192.
Ji Xiao-dong and Zheng Bao-yu. Opportunistic relaying and outage analysis for physical-layer network coding[J]. Journal of Electronics & Information Technology,2011,33(5):1186-1192.
[6] Yang T,Yuan X,Ping L,et al.. A new physical-layer network coding scheme with eigen-direction alignment precoding for MIMO two-way relaying[J]. IEEE Transactions on Communications,2013,61(3):973-986.
[7] Duc Hiep V,Van Bien P,and Xuan Nam T. Physical network coding for bidirectional relay MIMO-SDM system[C]. Proceedings of the Advanced Technologies for Communications (ATC),Ho Chi Minh City,Vietnam,2013:141-146.
[8] Chang R Y,Lin S J,and Chung W H. Joint-denoiseand-forward protocol for multi-way relay networks[C]. Proceedings of the Signal and Information Processing Association Annual Summit and Conference (APSIPA),Kaohsiung,China,2013:1-4.
[9] Chen M and Yener A. Multiuser two-way relaying:detection and interference management strategies[J]. IEEE Transactions on Wireless Communications,2009,8(8):4296-4305.
[10] Mengali U and D,Andrea A N. Synchronization Techniques for Digital Receivers[M]. New York:Plenum Press,1997:353-515.
[11] 季仲梅,杨洪生,王大鸣,等. 通信中的同步技术及应用[M].北京:清华大学出版社,2008:137-148.
[12] Zhang S,Liew S C,and Lam P. On the synchronization of physical-layer network coding[C]. Proceedings of the Information Theory Workshop,Chengdu,China,2006:404-408.
[13] Lu L and Liew S C. Asynchronous physical-layer network coding[J]. IEEE Transactions on Wireless Communications,2012,11(2):819-831.
[14] Rohrs U H and Linde L P. Some unique properties and applications of perfect squares minimum phase CAZAC sequences[C]. Proceedings of the Communications and Signal Processing,Cape Town,South Africa,1992:155-160.
[15] Feher K. Digital Communications:Satellite/Earth Station Engineering[M]. New Jersey:Prentice Hall,1983:346-396.
[16] D,Andrea A N,Mengali U,and Reggiannini R. The modified Cramer-Rao bound and its application to synchronization problems[J]. IEEE Transactions on Communications,1994,42(2/4):1391-1399.
[17] Ozaki K,Tomitsuka K,Okazaki A,et al.. Channel estimation technique for OFDM systems spread by chirp sequences[C]. Proceedings of the 2012 IEEE 23rd International Symposium on Personal Indoor and Mobile Radio Communications(PIMRC),Sydney,Australia,2012:2125-2130.
党小宇: 男,1973年生,博士,副教授,研究方向为卫星导航、信道编码理论、深空通信.
李 强: 男,1992年生,硕士生,研究方向为同步、信道编码理论、调制解调技术.
虞湘宾: 男,1970年生,博士,教授,研究方向为通信理论优化.
王旭东: 男,1978年生,博士,副教授,研究方向为信号检测、参数估计、高速信号处理的FPGA验证.
Symbol Timing Estimation for Physical-layer Network Coding
Dang Xiao-yu Li Qiang Yu Xiang-bin Wang Xu-dong
(College of Electronic Information Engineering,Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)
Most of the existing research on Physical-layer Network Coding (PNC) is based on the assumption that the symbol timing at the relay is ideally synchronized,and rarely discusses the issue of symbol synchronization. However,in practice,the symbol timing is indispensable in PNC systems. To tackle this problem,this paper proposes a novel symbol timing estimation scheme based on the orthogonal training sequences for PNC in two-way relay channels. According to the maximum-likelihood estimation criterion,a Discrete Fourier Transformation(DFT) based interpolation algorithm is applied to improve the estimation accuracy. It is shown by analysis and simulation that the proposed DFT-based symbol timing estimator exhibits superior performance. The Mean Square Error (MSE) performance of the estimator is one order of magnitude better than that of the conventional optimum sample algorithm for Signal-to-Noise Ratio (SNR) greater than 10 dB,and is very close to the Modified Cramer-Rao Bound (MCRB).
Wireless communication;Physical-layer network coding;Two-way relay channels;Symbol timing estimation;Modified Cramer-Rao Bound (MCRB)
TN919.3
A
1009-5896(2015)07-1569-06
10.11999/JEIT141364
2014-10-27收到,2015-01-06改回,2-15-05-11网络优先出版
国家自然科学基金(61172078,61201208),教育部留学回国人员科研启动基金和中央高校基本科研业务费(NS2014038)资助课题
*通信作者:李强 larmand@163.com

