基于影响函数的k-近邻分类
职为梅 张 婷 范 明
(郑州大学信息工程学院 郑州 450052)
基于影响函数的k-近邻分类
职为梅*张 婷 范 明
(郑州大学信息工程学院 郑州 450052)
分类是一种监督学习方法,通过在训练数据集学习模型判定未知样本的类标号。与传统的分类思想不同,该文从影响函数的角度理解分类,即从训练样本集对未知样本的影响来判定未知样本的类标号。首先介绍基于影响函数分类的思想;其次给出影响函数的定义,设计3种影响函数;最后基于这3种影响函数,提出基于影响函数的k-近邻(kNN)分类方法。并将该方法应用到非平衡数据集分类中。在18个UCI数据集上的实验结果表明,基于影响函数的k-近邻分类方法的分类性能好于传统的k-近邻分类方法,且对非平衡数据集分类有效。
数据挖掘;监督学习;非平衡数据集分类;影响函数;k-近邻
1 引言
分类是一种监督学习方法[1],已有的研究提出很多经典的分类方法,例如,决策树归纳[2]、朴素贝叶斯法[3]、神经网络[4]、支持向量机[5]、k-近邻(k-Nearest Neighbor,kNN)[6]、基于案例的推理[7]等。这些分类方法的做法相似,即,给定一个训练集 D,学习一个模型M,对于未知样本x,由M给出x的类标号。如果没有类标号已知的样本和其他先验知识,则除了随机猜测之外,没有更好的方法确定x的类标号。如果没有类标号已知的样本,但有某种先验知识,例如知道每个类出现的概率,则推断x属于出现概率最大的类的出错可能性更小。换句话说,利用先验知识推断胜过随机猜测。如果有已知类标号的训练样本集D,则可以在D上训练一个分类模型M(如决策树归纳、朴素贝叶斯、神经网络、支持向量机等)并用M对x分类,或者保留D并直接利用D推断x所属的类(如k -近邻、基于案例的推理等)。借助于训练样本集,合理的分类算法远比随机猜测和仅利用简单的先验知识好得多。
一般的分类算法都是基于训练数据集学习得到分类器分类未知样本,因此它们都受到训练数据集的影响。假设训练集为空集,不管一个分类算法多么优秀,对于未知样本,也只能采用随机猜测的方法分类未知样本;如果训练集无限大,包含了所有可能的实例,不管一个分类算法多么糟糕,分类准确率很容易达到百分之百;如果训练集D非空也没有包含所有的样本,那么分类算法基于训练集学习分类器分类未知样本。基于此,可以换个角度理解分类,即分类的过程也就是考察训练样本对未知样本x的影响。训练集为空,D对x的影响为0,只能随机猜测未知样本的类标号;训练集无限大,一定存在某一个类对x的影响为1,这个类的标号即为x的类标号;如果训练集为有限集合,假设D只包含了两个类C1和C2,如果C1类所有训练样本对x的影响大于C2类样本对x的影响,则x的类标号就为C1类。反之亦然。
基于以上分析,和传统的分类方法不同,从另一个角度看待分类问题,即,从训练数据集对未知样本的影响[8]角度出发看待分类。本文从新的角度阐述分类,提出基于影响函数的分类思想,也即,每个训练实例都对未知样本有一定的影响,综合所有训练样本对未知样本的影响,即可判定未知样本的类标号。严格地说,基于影响函数的分类不是一种分类算法,而是一种分类范型。定义不同的影响函数导致不同的分类算法。本文给出了3种影响函数的定义,基于这3种影响函数,提出了基于影响函数的k-近邻分类方法,UCI数据集上的实验结果表明,相对于普通的k-近邻分类方法,该方法可以提高分类的性能。
论文剩余部分组织如下:第2节介绍影响函数的定义,设计3种影响函数,并提出基于影响函数的k-近邻分类;第3节给出实验结果及相关评述;第4节给出基于影响函数的k-近邻分类方法在非平衡数据集上的分类效果;第5节总结全文。
2 基于影响函数的k-近邻分类
设训练数据集D包含L个类C1,C2,…,CL,Dl为第l类训练样本的集合,x为待分类实例。基于影响函数分类的基本思想是:定义 L个实型函数fl(x),l= 1,2,…, L。其中,fl(x)计算Dl中样本对x的影响。将待分类实例x分配到对x影响最大的类:如果,则把x分配到Cj类。
当只有两个类(L = 2)时,问题可以简化为:定义一个实型影响函数f(x)=f1(x)-f2(x),计算D中样本对x的影响。如果 f( x )≥ 0,则把x分配到C1类,否则把x分配到C2类。
k-近邻分类是一个经典的分类方法[6],从影响函数的角度更容易理解k-近邻分类。考虑未知样本x的某个领域,比如距离它最近的k个近邻,定义影响函数,计算这k个近邻对x的影响,将x划归为对它影响最大的那个类。下面就通过定义不同的影响函数,分析基于影响函数的k-近邻分类方法的性能。
2.1 影响函数的定义
影响函数的定义范围可以是全局的,也可以是局部的[8]。全局影响函数指每个训练实例都对 x有影响;局部影响函数指只有x的那些近邻才对x有影响。全局影响函数也很容易变换成局部影响函数,下面以全局影响函数为例介绍影响函数的定义方法:
(1)定义单个训练实例 'x对x的影响g('x,x);
(2)数据集D对x的影响 fD(x)可以定义为数据集中训练实例对x的影响的加权和:
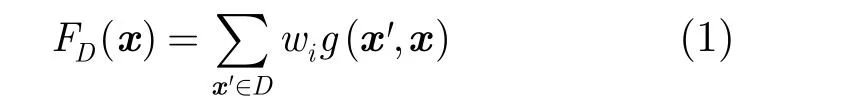
其中wi是实例 'x的权重,它反映 'x的重要性。在最简单的情况下,所有实例都取相等权重。当数据集D为第i类训练样本时,fD(x)简记为fi(x)。
训练实例 'x对 x的影响 g('x,x)的定义也有很多种方式,最简单的,0/1影响:如果 'x和x满足某个谓词,则 'x对x的影响为1,否则为0。这里,简单的“谓词”可以是“ 'x是x的k个最近邻之一”,“ 'x在 x的 -ε邻域内”。更复杂的谓词可以是,例如,分类规则的前件。除了0/1影响外,本文还设计了3种影响:
(1)线性影响:'x对x的影响随 'x与x的距离增加而线性减小。

其中,d('x,x)是 'x与x之间的距离,而dmax是训练实例之间的最大距离。
(2)平方影响:'x对x的影响随 'x与x的距离增加而平方减小。
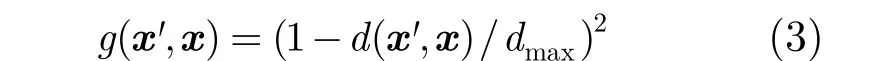
(3)指数影响:'x对x的影响随 'x与x的距离增加而指数衰减。
其中,α是一个待定常数,用于控制衰减速度。
2.2 算法描述
有了训练实例对未知样本的影响函数,可以对传统的k-近邻分类方法加以改进,得到基于影响函数的 k-近邻分类方法,其算法的具体过程见表 1。首先遍历D得到x的k个近邻Dz,对于Dz中每个实例 'x,根据影响函数的定义,计算它对x的影响,得到Dz每个类对x的影响函数值fl(x),将x的类标号设为fl(x)最大的那个类。
3 实验
3.1 数据集和实验设置
18个数据集从UCI机器学习库中随机选取[9]。对于每个数据集,采用5×2折交叉验证分析算法的性能。数据集的详细情况如表2所示。所有实验均基于weka平台。

表1 算法描述
3.2 实验结果
实验时,本文对比了朴素贝叶斯算法[3](Navie Bayes,NB)、支持向量机算法[5](Support Vector Machine,SVM)、判定树算法[2](Decision Tree,常用的判定树算法是 C4.5)、神经网络算法[4](Neural Network,NN),k-近邻分类(k-Nearest Neighbor,kNN)、基于线性影响的 k-近邻分类(Linear Effect kNN,LE-kNN)、基于平方影响的 k-近邻分类(Square Effect kNN,SE-kNN)和基于指数影响的k-近邻分类(Exponential Effect kNN,EE-kNN)。kNN,LE-kNN,SE-kNN以及EE-kNN 4四个算法都存在确定k值的问题,传统的k-近邻算法,k的值一般为3,因此在实验中,首先给出k值为3时,kNN,LE-kNN,SE-kNN以及EE-kNN在准确率上的结果,结果如表3所示。基于影响函数的分类中,如果考虑的实例少,效果不太好,为了对比实例多少对算法性能的影响,实验时改变k值的大小,分别取k为10,25,50,实验结果分别如表4~表6所示。
由表3可以发现,当k值取3的时候,神经网络的平均效果最好,支持向量机和神经网络比kNN的效果都好。而LE-kNN,SE-kNN,EE-kNN和kNN相比,kNN的效果最好,在15个数据集上的准确率值都超过了其他3三个算法,kNN在这18个数据集上的平均准确率值也最高,为80.05,LE-kNN,SE-kNN和EE-kNN的分别为73.84,73.51和79.88。这个结果不难理解,kNN算法通常取值为3,而基于影响函数的kNN算法,如果考虑的实例少时,效果不好。随着k值的增加,基于影响函数的kNN算法性能变好。
如表4所示,当k取值为10时,仍旧是神经网络的效果最好,但是LE-kNN和SE-kNN的平均准确率有明显提高,LE-kNN由 73.84提高到79.97,SE-kNN由73.51提高到79.46。相比于LE-kNN,SE-kNN,EE-kNN的还是性能最好,LE-kNN在这18个数据集上的平均准确率值也最高。可以看出,LE-kNN和kNN的性能相差无几。对比表3和表4可以发现,LE-kNN的性能在上升,而kNN的性能在下降。当k取值为25时,结果如表5所示,SE-kNN的性能最好,在这18个数据集上的平均准确率值也最高,为81.67,LE-kNN,EE-kNN,kNN,NB,SVM,C4.5和 NN的分别为 81.55,76.19,77.07,75.24,80.77,78.29和81.33,很明显LE-kNN的结果要比kNN,NB,SVM,C4.5和NN都好。对比表3,表4,表5发现,LE-kNN和SE-kNN的性能仍旧上升,kNN的性能仍旧下降。并且LE-kNN和SE-kNN的平均准确率同时超过神经网络。当k取值为50时,结果如表6所示,SE-kNN的性能仍旧最好,在这18个数据集上的平均准确率值也最高,为 81.54,LE-kNN,EE-kNN,kNN,NB,SVM,C4.5和NN的分别为79.91,73.81,74.33,75.24,80.77,78.29和81.33。

表2 实验数据集信息
表3~表6的结果表明,随着k值的增加,LE-kNN和SE-kNN的分类准确率增加,当k值增加到一定大小时,准确率的值也趋于稳定。对于k的取值,本文做了大量的实验,发现当k的值在20~50时,LE-kNN和SE-kNN的性能最好。达到相同的准确率值时,LE-kNN比SE-kNN取的k值要小一些。同时,还发现了一个有趣的现象,在大多数数据集上,EE-kNN在k值较小时达到最优性能,并且,EE-kNN在大多数数据集上的结果和kNN的结果相似,如表3所示。仔细观察表3~表6可以发现,当k值很小的时候,LE-kNN,SE-kNN在某些数据集上准确率值很差,比如tic-tac-toe,随着k值的增加,效果越来越好,当k达到一个特定值后,准确率值不再升高。而EE-kNN正好相反,当k值小的时候它在tic-tac-toe上的准确率值很高,随着k值的增加,准确率不升反降,这是一个有趣的现象。本文发现,在另外的一些数据集上也存在这样的现象。

表3 LE-kNN,SE-kNN,EE-kNN及kNN分类准确率的结果(k=3)

表4 LE-kNN,SE-kNN,EE-kNN及kNN分类准确率的结果(k=10)

表5 LE-kNN,SE-kNN,EE-kNN及kNN分类准确率的结果(k=25)

表6 LE-kNN,SE-kNN,EE-kNN及kNN分类准确率的结果(k=50)
表3~表6的实验结果表明,当影响函数设置得当时,基于影响函数的kNN分类可以提高分类的效果,并且正如所预测的那样,基于影响函数的kNN,需要一定数目的近邻来计算影响函数的值,如果考虑的近邻数目过少,效果不明显,考虑了足够多的近邻时,往往可以极大提高基于影响函数的kNN的分类性能。
3.3 局部性确定
传统的k-近邻学习算法通常将其设置为3,但是基于影响函数的k-近邻算法中,如果k的值很小,意味着影响未知样本x的训练样本少,效果非常差,应该为k选择一个适当的值。本小节中,本文设计了一组实验,学习最佳k值,论文随机选择两个数据集作为代表数据集学习最佳k值,分别是breastcancer和cleve。实验结果如图1和图2所示。
图1和图2分别给出 3种影响函数在 breastcancer和cleve上的结果。这两个图有一个共同特点,即线性影响和平方影响随着k值的增加性能变好,当k达到一定时(对于线性影响来说通常为25,平方影响为50),准确率趋于稳定。对于指数影响来说,随着k值的增加性能往往下降,k值在3~10之间性能最好。对于线性影响k值取15~50,对于平方影响k值取20~50。
4 影响函数分类用于非平衡数据集
基于影响函数的k近邻分类方法通过考察未知样本x的近邻对x的影响确定它的类标号,对它影响大的样本的类标号就是它的类标号,这种分类的思想也适合于非平衡数据集分类,非平衡数据集分类是数据挖掘中的一个难点问题,也是数据挖掘中的一个热点问题[10-16]。为了验证基于影响函数的分类对非平衡数据集分类有效,本文选择了两个常用的非平衡数据集:breast-cancer和sick(sick数据集的不平衡程度高,故在实验部分没有选择它作为数据集),对比了kNN,LE-kNN,SE-kNN在这些数据集上的分类效果(由3.2节知EE-kNN性能和kNN相似,故在此不再对比EE-kNN),使用非平衡数据集分类常用的衡量标准 f-度量、召回率来衡量分类效果的好坏,并且只给出了少数类上的 f-度量和召回率。结果如图3和图4所示。
Breast-cancer数据集有9个属性,286条实例,包含复发事件(recurrence-events)和非复发事件(no-recurrence-events)两个类,其中复发事件类为少数类,有85条实例,非复发事件类为多数类,有201条实例。由图4可以发现,LE-kNN和SE-kNN在复发事件类上的召回率和 f-度量都明显好于kNN。
sick数据集有 30个属性,3772条实例,包含negative和sick两个类,其中sick类为少数类,有231条实例,0类为多数类,有3541条实例。由图4可以发现,LE-kNN和SE-kNN在sick类上的召回率和f-度量都明显好于kNN,并且随着k值的增加,这3个算法的性能都下降。
在这2个数据集上的实验结果表明基于影响函数的分类方法的确对非平衡数据集分类有效。在此,本文只是简单的将LE-kNN和SE-kNN算法应用于二元的非平衡数据集分类中(实验中使用的2个数据集都是二元数据集),我们工作的下一步是设计更好的影响函数,并推广到多元的非平衡数据集分类中去。
5 总结

图1 LE-kNN,SE-kNN,EE-kNN在breast-cancer 上的准确率值

图2 LE-kNN,SE-kNN,EE-kNN在cleve 上的准确率值

图3 kNN,LE-kNN,SE-kNN 在breast-cancer上的召回率和f-度量
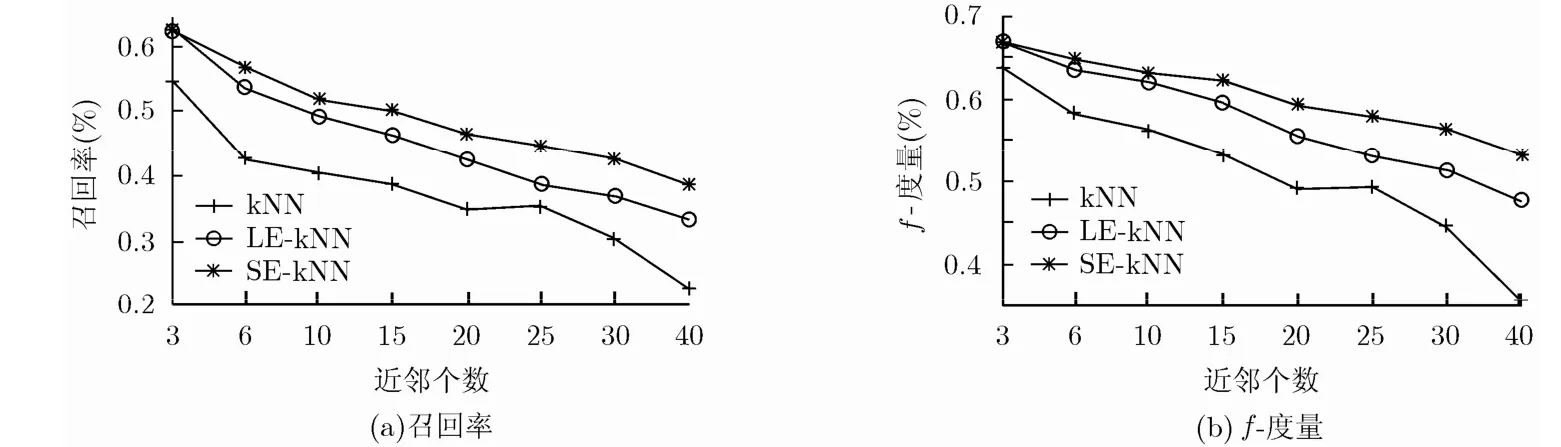
图4 kNN,LE-kNN,SE-kNN 在sick上的召回率和f-度量
本文从一个新的角度理解分类问题,即,从训练数据集对未知样本的影响角度出发看待分类。本文给出了几种影响函数的定义方法,并将这些影响函数的定义运用到k-近邻算法中,介绍了基于影响函数的k-近邻分类方法。通过实验对比,发现基于影响函数的k-近邻分类方法的确比普通的k-近邻分类方法性能好,当选定合适的k值时,基于影响函数的k-近邻算法并常用的分类算法性能还好。但是基于影响函数的k-近邻分类算法往往比普通的k-近邻分类方法需要考虑更多的近邻。本文中,将基于影响函数的分类方法应用与非平衡数据集分类中,发现该方法对于非平衡数据集分类也有效,我们工作的下一步是设计更复杂的影响函数,并推广至多元的非平衡数据集分类中去。考虑将基于影响函数分类和支持向量机和神经网络方法结合起来,进一步提高分类的性能。
[1] Tan P N and Steinbach M著,范明,范宏建,译. 数据挖掘入门[M]. 第2版,北京:人民邮电出版社,2011:127-187.
[2] Quinlan J S. Induction of decision trees[J]. Machine Learning,1986,1(1):81-106.
[3] Domingos P and Pazzani M J. Beyond independence:conditions for the optimality of the simple bayesian classifier[C]. Proceedings of the International Conference on Machine Learning,Bari,Italy,1996:105-112.
[4] Rumelhart D E,Hinton G E,and Williams R J. Learning representations by back-propagating errors[J]. Nature,1986,323(9):533-536.
[5] Boser B E,Guyon I M,and Vapnik V N. A training algorithm for optimal margin classifiers[C]. Proceedings of the Conference on Learning Theory,Pittsburgh,USA,1992:144-152.
[6] Dasarathy B V. Nearest Neighbor (NN) norms:NN Pattern Classification Techniques[M]. Michigan:IEEE Computer Society Press,1991:64-85.
[7] Leake D B. Experience,introspection and expertise:learning to refine the case-based reasoning process[J]. Journal of Experimental & Theoretical Artificial Intelligent,1996,8(3/4):319-339.
[8] Hinneburg A and Keim D A. An efficient approach to clustering in large multimedia databases with noise[C]. Proceedings of the Knowledge Discovery and Data Mining,New York,USA,1998:58-65.
[9] Bache K and Lichman M. UCI repository of machine learning databases[OL]. http://www.ics.uci.edu/~mlearn/MLRepository. html. 2014.5.
[10] Liu X Y,Li Q Q,and Zhou Z H. Learning imbalanced multi-class data with optimal dichotomy weights[C]. Proceedings of the 13th IEEE International Conference on Data Mining,Dallas,USA,2013:478-487.
[11] He H B and Edwardo A G. Learning from imbalanced Data[J]. IEEE Transactions on Knowledge and Data Engineering,2009,21(9):1263-1284.
[12] Maratea A,Petrosino A,and Manzo M. Adjusted F-measure and kernel scaling for imbalanced data learning[J]. Information Sciences,2014(257):331-341.
[13] Wang S and Yao X. Multiclass imbalance problems:analysis and potential solutions[J]. IEEE Transactions on Systems,Man and Cybernetics, Part B,2012,42(4):1119-1130.
[14] Lin M,Tang K,and Yao X. Dynamic sampling approach to training neural networks for multiclass imbalance classification[J]. IEEE Transactions on Neural Networks and Learning Systems,2013,24(4):647-660.
[15] Peng L Z,Zhang H L,Yang B,et al.. A new approach for imbalanced data classification based on data gravitation[J]. Information Sciences,2014(288):347-373.
[16] Menardi G and Torelli N. Training and assessing classification rules with imbalanced data[J]. Data Mining and Knowledge Discovery,2014,28(1):92-122.
职为梅: 女,1977年生,博士生,讲师,研究方向为数据挖掘、机器学习、人工智能.
张 婷: 女,1988年生,硕士,研究方向为数据挖掘、机器学习、人工智能.
范 明: 男,1948年生,教授,博士生导师,研究方向为数据挖掘、模式识别、人工智能.
k-nearest Neighbor Classification Based on Influence Function
Zhi Wei-mei Zhang Ting Fan Ming
(College of Information Engineering, Zhengzhou University, Zhengzhou 450052,China)
Classification is a supervised learning. It determines the class label of an unlabeled instance by learning model based on the training dataset. Unlike traditional classification,this paper views classification problem from another perspective,that is influential function. That is,the class label of an unlabeled instance is determined by the influence of the training data set. Firstly,the idea of classification is introduced based on influence function. Secondly,the definition of influence function is given and three influence functions are designed. Finally,this paper proposes k-nearest neighbor classification method based on these three influence functions and applies it to the classification of imbalanced data sets. The experimental results on 18 UCI data sets show that the proposed method improves effectively the k-nearest neighbor generalization ability. Besides,the proposed method is effective for imbalanced classification.
Data mining;Supervised learning;Classification of imbalanced data sets;Influence function;k-Nearest Neighbor (kNN)
TP181
A
1009-5896(2015)07-1626-07
10.11999/JEIT141433
2014-11-13收到,2015-04-03改回,2015-06-01网络优先出版
国家自然科学基金(61170223)和河南省教育厅科学技术研究重点项目(14A520016)资助课题
*通信作者:职为梅 iewmzhi@zzu.edu.cn

