机载顺轨干涉合成孔径雷达定标中地面控制点的布设策略研究
张 慧 洪 峻 王 宇 李纪传
①(中国科学院电子学研究所 北京 100190)
②(中国科学院大学 北京 100049)
③(空间信息处理与应用系统技术重点实验室 北京 100190)
机载顺轨干涉合成孔径雷达定标中地面控制点的布设策略研究
张 慧*①②③洪 峻①王 宇①李纪传①②
①(中国科学院电子学研究所 北京 100190)
②(中国科学院大学 北京 100049)
③(空间信息处理与应用系统技术重点实验室 北京 100190)
机载顺轨干涉合成孔径雷达(ATI-SAR)估计运动目标径向速度的精度受干涉相位误差、基线分量误差等影响,因此为了得到较高的测速精度必须对ATI-SAR的系统参数进行定标处理。基于敏感度方程的定标方法是干涉SAR定标中的常用方法,但是其性能受敏感度矩阵条件数的影响,地面控制点(GCP)或角反射器的布设方式决定了敏感度矩阵的条件数大小。该文通过分析给出机载ATI-SAR系统定标中GCP的布设策略,包括静止GCP的布设方式及运动GCP的数量、布设位置、运动速度大小和方向的设置原则,并通过仿真手段对上述布设策略进行了验证。
合成孔径雷达;顺轨干涉;定标;地面控制点;矩阵条件数
1 引言
机载顺轨干涉合成孔径雷达(Along-Track Interferometric SAR,ATI-SAR)最早由文献[1]提出,其利用两个(或两个以上)沿载机飞行方向放置的天线以一定的时间间隔先后对同一场景进行成像。载机飞行过程中两个天线运动到同一位置时与静止目标的斜距相同而与运动目标的斜距不同,从而使两个天线的成像结果进行干涉处理时,静止目标对应的相位相互抵消而运动目标对应的干涉相位被保留下来,且相位大小与目标的径向速度成正比,由此可以根据干涉相位检测运动目标并估计运动目标的径向速度。由于 ATI-SAR具有检测慢速运动目标径向速度的能力,因此被广泛应用于海面洋流检测[24]-和地面动目标检测[5,6]领域。载机飞行的不稳定性以及系统参数的定标精度是影响机载顺轨干涉SAR测速精度的主要因素,其中SAR平台的不稳定性可以在处理阶段得到校正[7]。为了获得较高的测速精度,必须对机载 ATI-SAR系统参数进行定标处理[810]-。基于敏感度方程的定标方法是干涉SAR中常用的定标方法[11],在顺轨干涉SAR的定标中,敏感度方程建立了目标测速误差与系统参数估计误差之间的联系。基于敏感度方程的定标方法的定标性能与敏感度矩阵的病态性有关,而矩阵的病态性可以由矩阵条件数来描述。影响敏感度矩阵条件数的因素包括待定标参数的种类和数量、地面控制点(Ground Control Point,GCP)的个数以及控制点的布设方式[12],因此在定标参数一定的情况下需要选择合理的GCP布设方案,使敏感度矩阵的条件数最小。

图1 机载ATI-SAR成像几何
对于对地形高程敏感的交轨干涉 SAR(Cross-Track Interferometric SAR,XTI-SAR),文献[7]和文献[12]都对其定标中 GCP的布设方案进行了研究,其中文献[7]指出 XTI-SAR敏感度矩阵的条件数与待定标参数的数量及 GCP沿距离向的分布有关,并比较了不同待定标参数下 3种典型的 GCP布设方式所对应的矩阵条件数大小;文献[12]在文献[7]的基础上,进一步给出了定标器的布放规则及布放间距约束条件。虽然目前机载 ATI-SAR系统定标中仍然采用基于敏感度方程的定标方法标定干涉相位偏差及基线分量误差[13],但是目前没有文献对机载顺轨干涉SAR定标中的GCP布设策略进行分析和报道。鉴于此,本文根据顺轨干涉SAR的工作原理,分析了机载ATI-SAR定标中不同的GCP数量及布放方式对敏感度矩阵条件数的影响,同时分析了运动控制点的速度和位置的影响,提出了一种既能降低敏感度矩阵条件数又便于实施的 ATISAR定标的GCP布设方案。
本文的安排如下:第2节简单介绍了ATI的测速原理及基于敏感度方程的定标方法;第3节分析了不同的 GCP布设方式对敏感度矩阵条件数的影响,包括静止GCP沿距离向的布设方式及运动GCP的速度和位置的设置,并通过仿真手段对各种布设条件下的矩阵条件数进行了比较,给出了较优的GCP设置方案;第4节为全文的总结部分。
2 测速原理及定标方法
2.1 ATI-SAR的工作原理
图1为正侧视情况下机载ATI-SAR的工作几何,图中的坐标系以O点为原点,O为方位零时刻参考天线相位中心的地面投影点,X轴平行于载机飞行的方向,Z轴竖直向上,Y轴与X,Z轴成左手坐标系。图中考虑了两个天线的运动轨迹不完全在同一条直线上排列的非理想情况。为简便,本文中假设ATI-SAR工作在“乒乓”工作模式[14],即两个天线交替地发射和接收自己发射的电磁波。此时由于目标沿径向的运动及垂直基线分量的存在引起的干涉相位大小为[15,16]:

其中,λ为波长,θ为下视角,基线矢量B在3个坐标轴方向的分量大小分别为顺轨基线分量xB、跨航向基线分量 yB和竖直方向基线分量 zB, tΔ 为两个天线到达同一位置所需的时间间隔,在“乒乓”模式下 Δt =Bx/,vppv为平台的运动速度。假设平台的高度为H,目标的高度与参考高程相同,设为0,则cos θ= H / R( t),其中 R( t)为t时刻参考天线与目标之间的最短斜距。由式(1)易得运动目标的径向速度表达式:
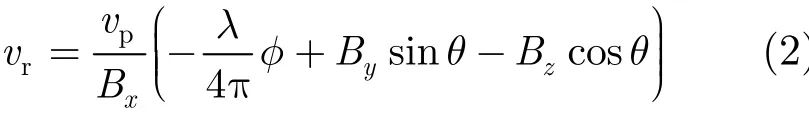
敏感度反映了各干涉参量的误差对目标径向速度精度的影响程度。将式(2)中目标径向速度rv关于各干涉参量求偏导数,即可得到目标径向速度关于上述各参量的敏感度,具体可参见文献[14],这里不再一一列举。
2.2 基于敏感度方程的ATI-SAR定标方法
敏感度方程建立了目标径向速度估计误差与干涉参量偏差之间的联系,即
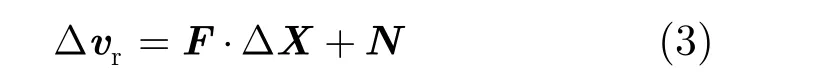
其中,rΔv为 1L× 的速度误差向量,F为L N× 的敏感度矩阵,N为噪声向量,ΔX为 1N× 的待估计参数的偏差组成的向量,。这里L为控制点的数量,N为待定标参数的数量,且L N≥ 。敏感度矩阵F表示为
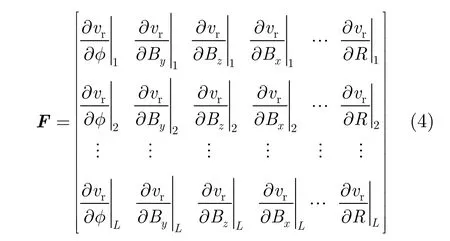
对于线性方程式(3),系数矩阵F的条件数越大,矩阵的病态性越强[17],由此引入的误差越大。因此在后面的定标点布设策略分析中,可以利用矩阵条件数作为衡量定标性能的工具之一。
3 机载ATI-SAR定标中GCP的布设策略
3.1 静止GCP的布设
顺轨干涉SAR对运动目标的径向速度敏感,但是运动的GCP在实际中难以控制。并且在标定干涉相位偏差和基线的两个垂直分量 By, Bz时,不需要运动控制点即可标定,因此为简便,本文选择静止目标对除顺轨基线分量xB以外的干涉参数进行定标。
对于机载ATI-SAR,当只考虑静止GCP并且忽略ATI时间间隔造成的时间去相干时,所布设静止GCP的相位大小完全由垂直基线分量引起,此时ATI-SAR系统等价于小基线的XTI-SAR系统。关于交轨干涉SAR定标中地面控制点的布设问题,文献[7]和文献[12]已通过理论分析和试验验证给出了GCP的布设原则,即所有GCP不能集中在某一区域,而是尽可能充满整个距离向测绘带,且沿方位向布设若干列。因此,与交轨干涉SAR定标中定标器的布设原则类似,ATI-SAR定标中静止GCP沿距离向布设时也应尽量充满整个测绘带。下面通过设置几种不同的静止GCP的布放方式,利用仿真的手段对各种布设方式下的矩阵条件数进行比较,从而对上述结论进行验证。
图2针对某一距离条带选择了8种不同的GCP布设方式,其中横轴代表距离向,假设所选定标场平坦且与参考高程相同。图中前3种布设方式为所有GCP集中在某一区域的情况,后5种布设方式中GCP以不同分布情况充满整个测绘带,各子图的布设方式分别为
布设方式1:所有GCP集中在近距端;
布设方式2:所有GCP集中在远距端;
布设方式3:所有GCP集中在测绘带中间;
布设方式4:所有GCP按照从近距端到远距端越来越稀疏的方式布满整个测绘带,相邻两个GCP之间的距离按照等差数列的方式递增;
布设方式5:同方式4,但是相邻两个GCP之间的距离按照等比数列的方式递增;
布设方式6:所有GCP按照从近距端到远距端越来越密集的方式布满整个测绘带,相邻两个GCP之间的距离按照等差数列的方式递减;
布设方式7:同方式6,但是相邻两个GCP之间的距离按照等比数列的方式递减;
布设方式8:所有GCP均匀布满整个测绘带。
利用表1中的仿真参数,对不同GCP数量下不同 GCP布设方式所对应的矩阵条件数大小进行比较,结果如图3所示。其中图3(a),3(c),3(e)为3种待定标参数情况下所有布设条件下的矩阵条件数,图3(b),3(d),3(f)为3种待定标参数情况下后5种布设方式所对应的矩阵条件数大小。

表1 载机仿真参数
由图3可得,随着待定标参数的增加,矩阵条件数增大;前3种GCP布设方式下的矩阵条件数远大于其他5种布设方式,即所有GCP都集中在某一区域时矩阵条件数较大,当GCP沿距离向充满整个距离条带时对应的矩阵条件数较小。因此静止GCP的布设方案可以归纳为:
(1)使所有静止GCP沿距离向尽可能充满整个距离条带。
考虑到载机飞行不稳定性主要体现在不同方位向之间,因此为了标定载机不稳定性的测量偏差,还需要在不同的方位时刻布设定标器,即:
(2)在方案(1)的基础上,定标器沿方位向布放若干列。
3.2 运动控制点的设置
顺轨干涉SAR中顺轨基线分量xB只有在存在运动目标时才对干涉相位有贡献,因此要在敏感度方程定标方法中直接对xB大小进行标定,至少需要一个运动GCP。关于运动GCP的布设,主要考虑运动GCP的数量、位置、速度的方向和大小对定标精度的影响。

图2 距离条带内不同的GCP布设方式
3.2.1 运动控制点的数量和位置设置 理想情况下如果控制点的速度、位置等信息的精度足够高,则只需采用一个运动GCP就能标定顺轨基线分量xB的大小。但是只选择一个运动GCP会增大偶然误差出现的概率,在试验条件允许的情况下可以设置多个运动GCP,以降低偶然误差出现的几率。理论上选择一个运动GCP与选择多个运动GCP所对应的矩阵条件数在同一量级上,仿真结果同样证明了这一点。而采用的运动GCP的个数越多,工程实现起来越困难,通过综合考虑,可以选取运动GCP的个数为1~3个,且各运动GCP的速度均应远离0值附近。本文中后续仿真中为简便,在分析运动 GCP的位置和速度设置时,均选择1个运动GCP进行分析。
在表1所示的仿真参数下,选择一个运动GCP,仿真该运动 GCP所在位置对敏感度矩阵条件数的影响。图4(a)~4(f)分别选取了4~9个GCP进行仿真,其中横坐标表示从近距端到远距端运动 GCP的序号(其他 GCP设为静止,且沿距离向均匀布设),纵坐标表示相应的矩阵条件数。
从图4中可以看出,当GCP的个数为L时,对各个GCP从近距到远距分别编号为1,2,,… L,则要使矩阵条件数最小,速度设置为非零的GCP的标号i应满足:
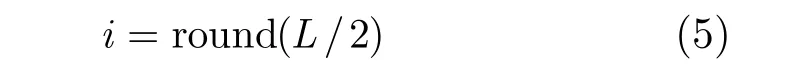
其中,round()·表示四舍五入,即L为偶数时,i L/=2 ;L为奇数时, i( = L1+) /2,即运动的GCP位于测绘带的中心。本次仿真中假设运动GCP的径向速度为0.5 m/s,选择其它速度值可以得到同样的结论。
3.2.2 运动控制点的速度大小和方向 在 ATI-SAR中,运动目标的径向速度影响干涉相位的大小,而方位向速度会影响图像的聚焦效果[18,19]。下面分别对运动 GCP的径向速度和方位向速度的设置原则进行讨论。(1)径向速度 为保证ATI-SAR干涉相位不发生缠绕,一般要求运动目标的径向速度小于 ATISAR的最大不模糊速度。在表1所列的仿真参数下,

图3 不同GCP布设形式下的矩阵条件数
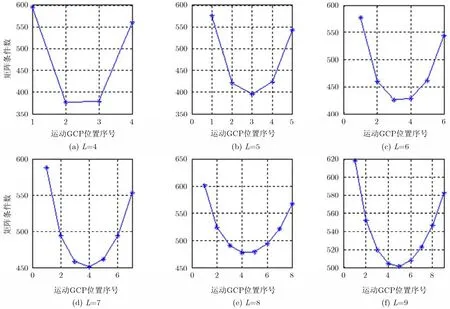
图4 不同控制点个数L下运动GCP的不同位置对矩阵条件数的影响
ATI的最大不模糊速度约为2.35 m/s。同时,在ATISAR动目标检测中,当由于目标径向速度引入的干涉相位较大(远离检测门限)时运动目标的径向速度更容易检测,因此在定标中运动GCP的径向速度应尽量大但不超过最大不模糊速度,在本文的仿真参数下可以选择在1~2 m/s左右,此类目标可选择为一辆配有GPS的小推车,如美国JPL用于验证机载ATI-SAR GMTI功能的试验[4]。另一方面,由于运动目标是作为控制点使用的,其速度和位置信息可以由配备的GPS等设备进行测量,因此当目标的径向速度偏大而导致干涉相位超出2π的范围时,相位缠绕的整数倍的数值是可以通过系统参数估计出来的,此时可以对ATI-SAR干涉相位进行精确解缠,利用解缠的相位和目标径向速度值标定顺轨基线分量xB。从这一方面讲,运动GCP的径向速度可以大于最大不模糊速度,此时可以选择带有角反射器及GPS的汽车、卡车等。因此,在不考虑运动目标径向速度对成像质量的影响的情况下,运动控制点的径向速度可以不受ATI-SAR最大不模糊速度的限制,从理论上讲,尽量保证干涉相位的相位主值的绝对值远离0值附近即可。
以一个运动GCP为例,图5仿真了不同GCP径向速度对应的敏感度矩阵条件数。图5的结果同样表明,当GCP的径向速度在0值附近时敏感度矩阵的条件数较大,即测量误差对定标结果的影响越大。
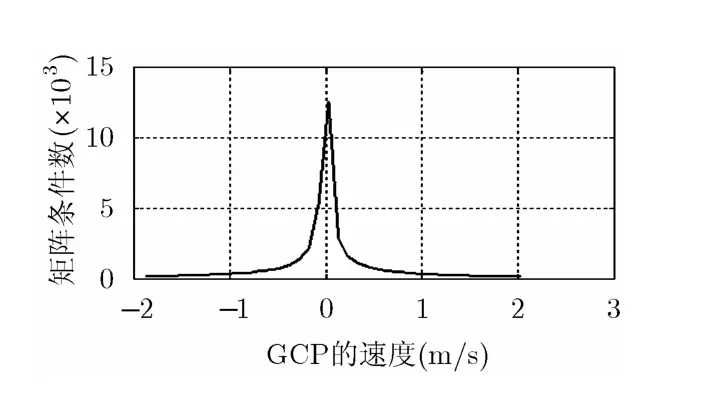
图5 GCP的径向速度对敏感度矩阵条件数的影响
(2)方位向速度 当运动目标存在方位向速度va时,运动目标的相位历程与方位压缩中参考相位历程不同从而产生方位模糊[18,19]。在方位压缩中,参考方位匹配滤波器对应的相位历程为

其中0R为最短斜距。忽略目标的径向速度和加速度,则运动目标的实际相位历程为
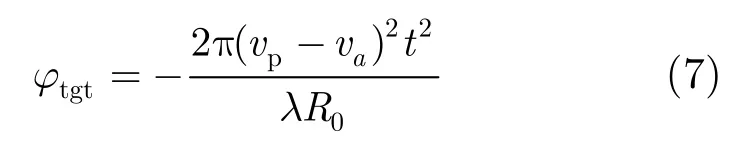
因此在一个合成孔径时间内二者之差造成的二次相位误差为
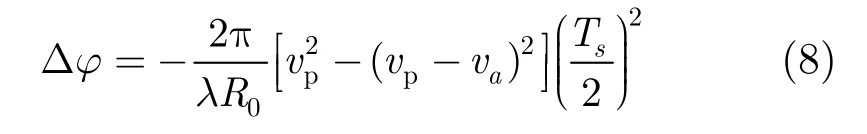
一般工程应用中,要保证图像不散焦,在合成孔径时间内二次相位误差应该不超过 /4π 。令式(8)中并假设 vp≫ va,则可以得到目标方位向速度的约束条件:
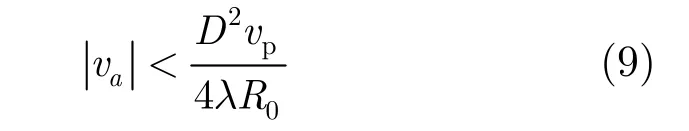
因此,为了减小目标方位向速度引起的图像模糊,应尽量使运动目标的运动方向与载机飞行方向垂直,从而保证目标的方位向速度近似为 0,满足不等式(9)的要求。以表1中的仿真参数为例,最短斜距取8000 m,则
综上,运动GCP的速度、位置设置规则可归纳为:
(1)运动GCP的运动方向应尽量垂直于载机的飞行方向,从而使目标方位向速度近似为零,满足不等式(9)的要求,以降低图像散焦;
(2)运动目标的径向速度或缠绕后的径向速度应尽量远离速度零值、接近ATI-SAR的最大不模糊速度;
(3)为简便可选择1个运动GCP,使其位于距离向测绘带的中心;如果选择2个或2个以上运动GCP,这些运动GCP与静止GCP的布设规则相同,且径向速度均不能接近0。
4 结束语
该文针对基于敏感度方程的机载 ATI-SAR干涉相位偏置误差、基线分量误差等的定标方法,研究了不同的GCP布设方案,包括静止GCP沿距离向的布设方式及运动GCP的速度、运动方向、位置的布设规则,提出了使敏感度矩阵条件数极小化的布设规则。仿真和分析证明,为得到较小的矩阵条件数,静止GCP应尽可能充满整个距离条带;要得到顺轨基线分量的准确值,需布设至少一个运动GCP,且运动GCP尽量选择在距离条带的中心,运动GCP的运动方向尽量垂直于载机飞行方向,径向速度或缠绕后的径向速度应尽量远离0值附近。该文的分析为机载顺轨干涉 SAR外定标试验的地面控制点布设提供了参考。
[1] Goldstein R M and Zebker H A. Interferometric radar measurement of ocean surface currents[J]. Nature,1987,328:470-475.
[2] Romeiser R,Runge H,Suchandt S,et al.. Quality assessment of surface current fields from TerraSAR-X and TanDEM-X along-track interferometry and Doppler centroid analysis[J]. IEEE Transactions on Geoscience and Remote Sensing,2014,52(5):2759-2772.
[3] Lopez D P,Rodriguez C M,Parts P,et al.. Experimental bidirectional SAR ATI acquisitions of the ocean surface with TanDEM-X[C]. 10th European Conference on Synthetic Aperture Radar (EUSAR),Berlin,Germany,2014:1-4.
[4] Goncharenko Y V and Farquharson G. ATI SAR signatures of nearshore ocean breaking waves obtained from field measurements[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS),Melbourne,Australia,2013:326-329.
[5] Stacy N and Preiss M. Polarimetric ATI slow target detection in a log likelihood framework[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium(IGARSS),Melbourne,Australia,2013:3163-3166.
[6] Imel D A. AIRSAR along-track interferometry data[R]. 4800 Oak Grove Drive,Pasadena,2002.
[7] Mallorqui J J,Bara M,and Broquetas A. Calibration requirements for airborne SAR interferometry[C]. Proceedings of SPIE,SAR Image Analysis,Modeling,and Techniques III, Barcelona,Spain,2000(4173):267-278.
[8] Deng H Z,Goncharenko Y V,and Farquharson G. Phase calibration of an along-track interferometric FMCW SAR[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne,Australia,2013:1649-1652.
[9] Hirsch O. Calibration of an airborne along-track interferometric SAR system for accurate measurement of velocities[C]. Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS),Sydney,Australia,2001(1):558-560.
[10] Zhang W D,Song N,Dong X W,et al.. Airborne SARATI-GMTI data processing[C]. Proceedings of the International Conference on Digital Manufacturing and Automation,Qingdao,China,2013:122-125.
[11] Mallorqui J J,Bara M,and Broquetas A. Sensitivity equations and calibration requirements on airborne interferometry[C]. Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS),Honolulu,America, 2000(6):2739-2741.
[12] 王彦平,彭海良,云日升. 机载干涉合成孔径雷达定标中的定标器布放[J]. 电子与信息学报,2004,26(1):89-94.
Wang Yan-ping,Peng Hai-liang,and Yun Ri-sheng. Locating calibrators in airborne InSAR calibration[J]. Journal of Electronics and Information Technology,2004,26(1):89-94.
[13] 王欣. 机载ATI-SAR基线定标方法研究[D]. [硕士论文],中国科学院电子学研究所,2012.
Wang Xin. Study on baseline calibration method for airborne ATI-SAR[D]. [Master dissertation],Institute of Electronics,Chinese Academy of Sciences,2012.
[14] Zhang Y H. Along Track Interferometry Synthetic Aperture Radar (ATI-SAR) techniques for ground moving target detection[R]. Final Technical Report,Hillside Terrace Marcy New York,2006.
[15] Moccia A and Rufino G. Spaceborne Along-Track SAR Interferometry:performance analysis and mission scenarios[J]. IEEE Transactions on Aerospace and Electronic Systems,2001,37(1):199-213.
[16] Zhang H and Hong J. Sensitivity analysis of Along-Track Interferometric Synthetic Aperture Radar (ATI-SAR) in the presence of squint[C]. Proceedings of the IET International Radar Conference,Xi'an,China,2013:1-5.
[17] 邹谋炎. 反卷积和信号复原[M]. 北京:国防工业出版社,2001:87-88,224-226.
Zou Mou-yan. Deconvolution and Signal Recovery[M]. Beijing:National Defence Industry Press,2001:87-88,224-226.
[18] Raney R K. Synthetic aperture imaging radar and moving targets [J]. IEEE Transactions on Aerospace and Electronic Systems,1971,AES-7(3):499-505.
[19] Chen C W. Performance assessment of along-track interferometry for detecting ground moving targets[C]. Proceedings of the IEEE Radar Conference,Wyndham,PA,USA,2004:99-104.
张 慧: 女,1987年生,博士生,研究方向为机载顺轨干涉SAR定标及处理.
洪 峻: 男,1960年生,研究员,研究方向为合成孔径雷达定标及定量遥感应用技术研究.
王 宇: 男,1976年生,副研究员,研究方向为机载SAR定标、雷达信号处理.
李纪传: 男,1988年生,博士生,研究方向为雷达信号处理.
Study on Ground Control Point Locating Strategy for Airborne Along-track Interferometric SAR
Zhang Hui①②③Hong Jun①Wang Yu①Li Ji-chuan①②
①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190,China)
②(University of Chinese Academy of Sciences, Beijing 100049,China)
③(Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Beijing 100190, China)
The accuracy of the radial velocity estimated by the airborne Along-Track Interferometric SAR(ATI-SAR) is affected by the accuracy of different system parameter,such as the interferometric phase biases and the baseline components errors. Therefore,these factors must be calibrated if the higher radial velocity estimation accuracy is required. The calibration methods based on the sensitivity equations are generally used in the interferometric SAR calibration. However,the performance of these methods is limited by the matrix condition number of the sensitivity matrix,which is decided by the location strategy of Ground Control Points (GCP). This study analyses and simulates the condition number of the sensitivity matrix corresponding to the different GCP distribution ways along the swath as well as the different selections of velocities and positions of moving ground control points.
SAR;Along-Track Interferometry (ATI);Calibration;Ground Control Point (GCP);Matrix condition number
TN959.73
A
1009-5896(2015)07-1716-07
10.11999/JEIT141220
2014-09-17收到,2015-02-15改回,2015-05-08网络优先出版
国家自然科学基金(61101200)资助课题
*通信作者:张慧 123happy.zh@163.com

